ESERCITAZIONE III _ DIMENSIONAMENTO DI UNA TRAVE A SBALZO

DIMENSIONAMENTO DI UNA TRAVE A SBALZO (MENSOLA)

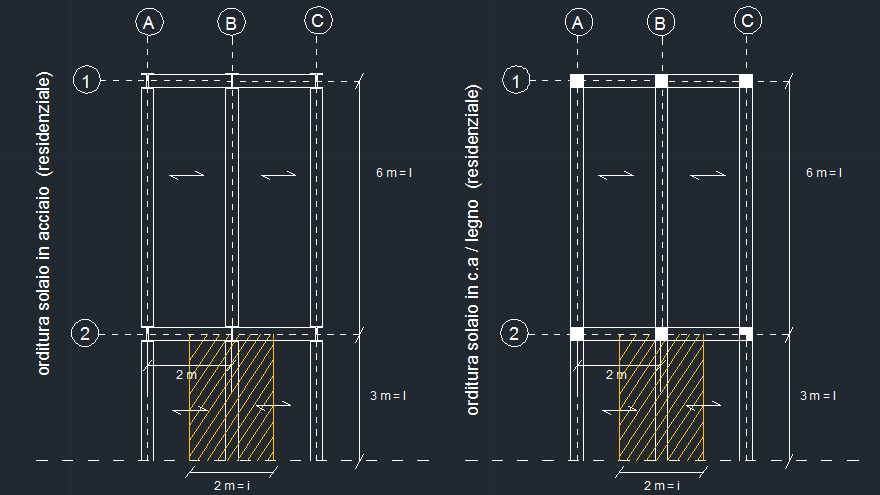
si consideri una trave a sbalzo (mensola) di un solaio con la seguente orditura per ciascuna delle tre tecnologie: legno/ acciaio/ cls.

  

DIMENSIONAMENTO DI UNA TRAVE A SBALZO (MENSOLA)_ LEGNO

 

1_ individuo la trave maggiormente sollecitata e ne vado a progettare l’ H (altezza della sezione):

la mensola su cui grava più carico è quella centrale:

luce= 3 m

interasse= 2m

Area di influenza= 2*3= 6 m²

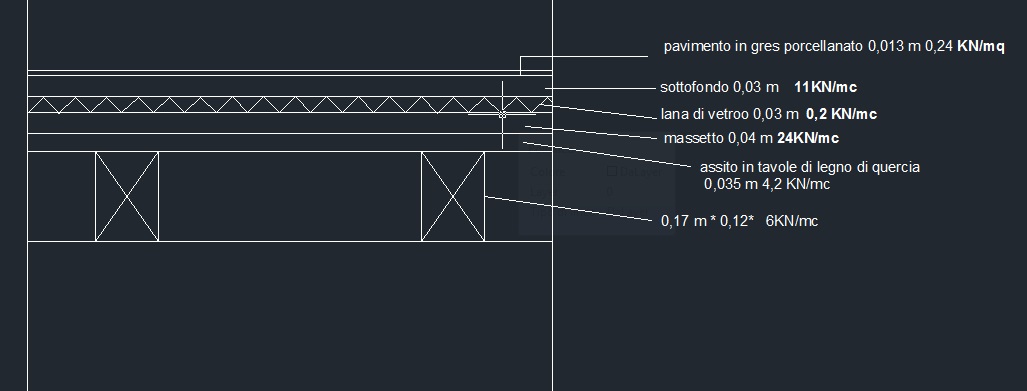
2_ In riferimento al solaio in legno analizzato nella prima esercitazione, vado ad inserire nel foglio Excel i carichi e l’ interasse:

q_s_ carichi strutturali  (tavolato/travetti)

q_s = 0,39 KN/m²

q_p_ carichi permanenti  (pavimento/sottofondo/isolante/massetto/intonaco/ impianti/tramezzi)

q_p = 3,80 KN/m²

q_a_ carichi accidentali  (normativa)

q_a = 2 KN/m²

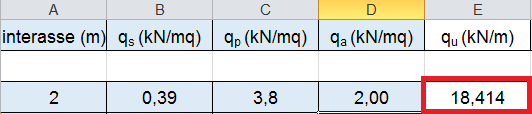
3_Il foglio Excell ha calcolato q_u (tot carichi lineari che gravano sulla trave)

q_u = 18,41 KN/m

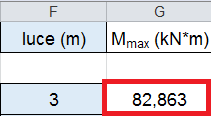
4_inserendo la luce(lo sbalzo della trave in esame)= 3m il foglio Excel ricaverà M_max

M_max=  (q_u x l)²/ 2 (secondo il modello semplice della mensola)

PROGETTO

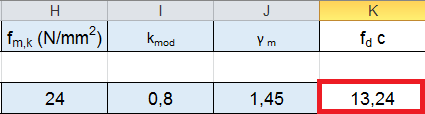
1_ scelgo la tecnologia, la classe e ricavo dalle tabelle la resistenza caratteristica a flessione f_m.k

Nella prima esercitazione ho scelto il legno lamellare di classe GL24h;

 f_m.k =24 KN/mm² (Mpa)

2_ora inserisco alcune informazioni relative alla geometria e al materiale che ho scelto inserendo i tre parametri:

f_m.k =24 KN/mm² (Mpa)

 k_mod= 0,8 (ricavato dalle tabelle in base alla durata del carico, classe di durata/ classe di servizio)

γ_m= 1,45 (coefficiente parziale di sicurezza)

grazie a questi il foglio Excel calcola la tensione di progetto

f_d (N/mm²) = K_mod*f_m,k/ γ_m

3_ ipotizzando una base b= 20 cm ricavo l’ altezza minima h_min = 43,33 cm,

essendo un predimensionamento di minima posso ingegnerizzare scegliendo un valore maggiore:   H=45 cm.

                                       

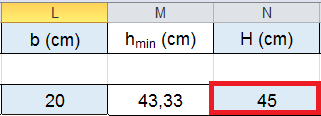
Non considero  il peso proprio della trave in legno in quanto leggera e quindi trascurabile. Considero la sezione 20X35cm.

VERIFICA ALLO STATO LIMITE DI ESERCIZIO

1_ Impostando il modulo elastico E = 8000 Mpa ,si ricavano:

I_x= b*h³/12 [cm⁴] = 151875 cm⁴

q_e= (q_s+ q_p+ q_a* 0,5)*interasse =( 0,39+3,80 +2,00 *0,5)*2= 10 KN/m (carico totale)

ora il foglio Excel ha tutti gli strumenti per calcolare l’ abbassamento massimo v_max e il suo rapporto con la luce l/v_max:

v_{max =} q_e*l⁴/8* E*I_x= 0,87 cm

l/ v_max= 346,82                                                                

CONCLUSIONE

La sezione è VERIFICATA  in quanto il rapporto tra la luce e l’abbassamento

l/ v_max≥  250₌ 346,82 ≥ 250 _ SI

OSSERVAZIONI

si noti nella formula il rapporto tra V e I_x/ V e q:

I_x è inversamente proporzionale a V ,quindi più aumenta il momento d’inerzia e più diminuisce l’abbassamento!

Mentre q è direttamente proporzionale a V , quindi più aumenta il carico e maggiore sarà l’abbassamento della trave a sbalzo!

Posso utilizzare una trave meno invasiva con un’ altezza H pari a 42 cm.

DIMENSIONAMENTO DI UNA TRAVE A SBALZO (MENSOLA)_ ACCIAIO

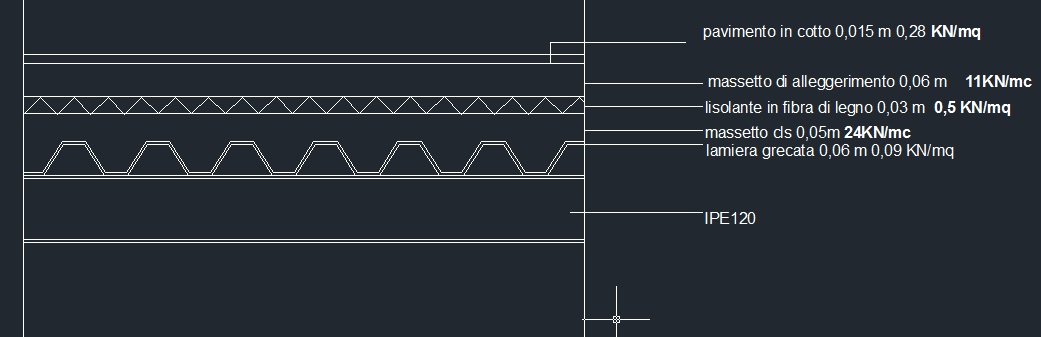
1_ In riferimento al solaio in acciaio analizzato nella prima esercitazione, vado ad inserire nel foglio Excel i carchi e l’ interasse  (orditura sovraindicata):

q_s_ carichi strutturali  (travatura secondaria IPE120/massetto cls/lamiera grecata)

q_s = 1,03 KN/m²

q_p_ carichi permanenti  (pavimento/mass. di alleggerimento /isolante/ impianti/tramezzi)

q_p = 2,49 KN/m²

q_a_ carichi accidentali  (normativa)

q_a = 2 KN/m²

3_Il foglio Excell ha calcolato q_u (tot carichi lineari che gravano sulla trave)

q_u = 16,148 KN/m

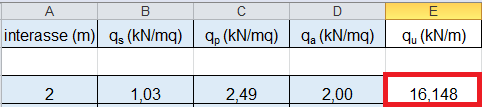
2_inserendo la luce(lo sbalzo della trave in esame)= 3m il foglio Excel ricaverà M_max

M_max=  (q_u x l)²/ 2 = 72,666 KNm(secondo il modello semplice della mensola)

                                             

PROGETTO

1_ scelgo la tecnologia e dalle tabelle ne ricavo la resistenza caratteristica f_yk

Nella prima esercitazione ho scelto la trave Fe 235N/mm² con f_yk= 235 N/mm²

il foglio Excel trova così un modulo di resistenza W_x,min=324,68 cm³

                                            

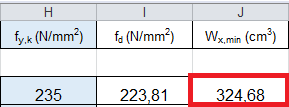
2_ ingegnerizzo: consultando le tabelle di produzione di travi standard vado a scegliere la mia trave in base al modulo di resistenza trovato.

La trave che sceglierò dovrà avere un W_x > W_xmin  ovvero W_x > 324,68

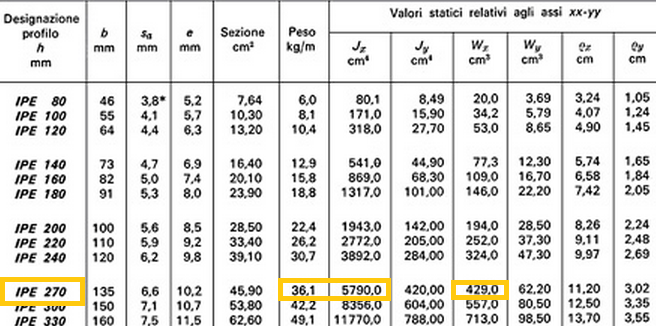
Considero il profilo IPE 270.

VERIFICA ALLO STATO LIMITE DI ESERCIZIO

3_ come indicato, nella tabella trovo anche il momento d’ inerzia I_x e il peso che inserisco nel foglio di calcolo che ricava q_e, il carico totale comprensivo del peso proprio della trave:

I_x = 5790 cm⁴

P=36,1 Kg/m = 0,361 KN/m

                                        

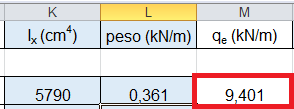
4_ inserisco il modulo elastico E = 210.000 N/mm²

Il fogli Excel ha ora tutti gli strumenti per calcolare l’ abbassamento massimo V_max e il suo rapporto con la luce l/ v_max

v_{max =} q_e*l⁴/8* E*I_x= 0,783 cm

l/ v_max= 383,22

CONCLUSIONE 

Il profilo IPE270 è VERIFICATO  in quanto il rapporto tra la luce e l’abbassamento è l/v_max≥ 250₌ 383,22 ≥ 250_SI

DIMENSIONAMENTO DI UNA TRAVE A SBALZO (MENSOLA)_ CLS

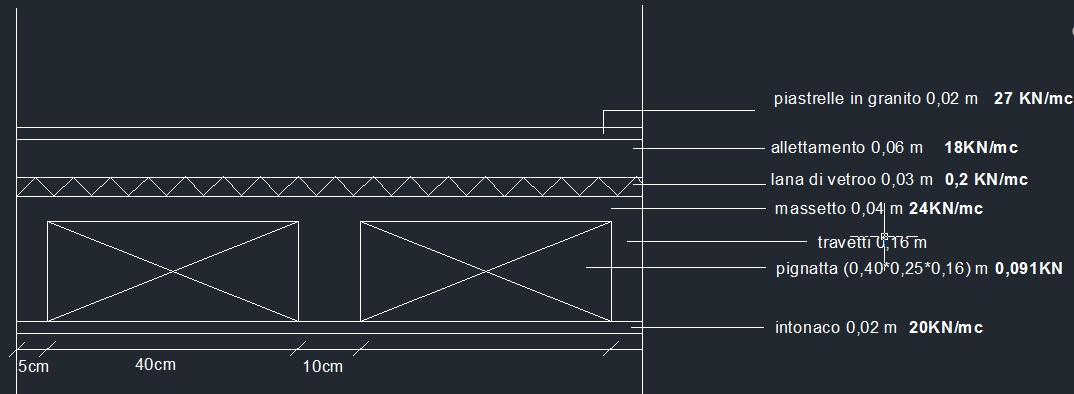
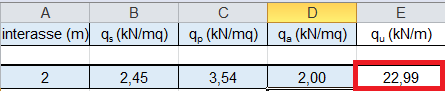
1_ In riferimento al solaio in cls analizzato nella prima esercitazione, vado ad inserire nel foglio Excel i carchi e l’ interasse  (orditura sovraindicata):

q_s_ carichi strutturali  (travetti/ pignatte/ soletta)

q_s = 2,45 KN/m²

q_p_ carichi permanenti  (pavimento/allettamento /isolante/intonaco/ impianti/tramezzi)

q_p = 3,53 KN/m²

q_a_ carichi accidentali  (normativa)

q_a = 2 KN/m²

3_Il foglio Excell ha calcolato q_u (tot carichi lineari che gravano sulla trave)

q_u = 22,99 KN/m

                            

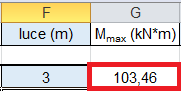
2_inserendo la luce(lo sbalzo della trave in esame)= 3m il foglio Excel ricaverà M_max

M_max=  (q_u x l)²/ 2 = 103,46 KNm (secondo il modello semplice della mensola)

                                                      

PROGETTO

1_ scelgo le resistenze caratteristiche dell’ acciaio f_yk e del cls f_ck che permetteranno al foglio Excel di calcolare le rispettive tensioni di progetto f_yd e f_cd, dove:

f_yd = f_yk /1,5

f_cd= f_ck *αcc / 0,85

quindi, inserisco

per l’ acciaio B450 C , la resistenza caratteristica a flessione fyk= 450 N/mm²

per il cls ,resistenza caratteristica a compressione f_ck = 60 N/mm²

                  

Oltre a calcoalare le f_d il foglio ha calcolato anche i parametri che permettono di calcolare l’ altezza utile  h_u  :

β =0, 57

r= 2,09

2_ ipotizzo ora che la base della mia trave possa essere di 20 cm

 b=20 cm

il foglio Excel ricava ora l’ H_min ( = h_u +δ) con δ= distanza compresa tra il baricentro dei tondini di armatura e l’estremo inferiore della trave , si trova

H_min= 30,74 cm che ingegnerizzo a un  H = 35 cm

Considero la sezione 20X 35 cm .

VERIFICA ALLO STATO LIMITE DI ESERCIZIO

1_ inserisco il modulo elastico E = 21000 N/mm²

Ora il foglio Excel ha tutti gli strumenti necessari per calcolare l’ abbassamento massimo V_max, e il suo rapporto con la luce l/v_max :

 v_max = q_e*l⁴/8* E*I_x = 1,06 cm

l/v_max = 282,66

         

CONCLUSIONE

La sezione 20X35 cm è VERIFICATA  in quanto il rapporto tra la luce e l’abbassamento è l/v_max≥ 250₌ 282,66 ≥ 250_SI

OSSERVAZIONI

Per cls altamente performanti,(con una maggiore resistenza caratteristica a compressione f_ck) ,avrò sicuramente una H minore (una sezione meno invadente) ,ma si abbasserà  il rapporto tra l/v_max!!!che infatti in questo caso non è accettabile perche è < 250!!