ESERCITAZIONE_3: VERIFICA DELLA DEFORMABILITÀ DI UNA MENSOLA

La terza esercitazione tratta il dimensionamento della sezione di una trave a sbalzo nei tre materiali: C.A., legno ed acciaio.

Come nell'esercitazione 2, l'impalcato si compone di travi principali e travi secondarie delle quali ho mantenuto costante l'interasse e la luce in tutte e tre le categorie.

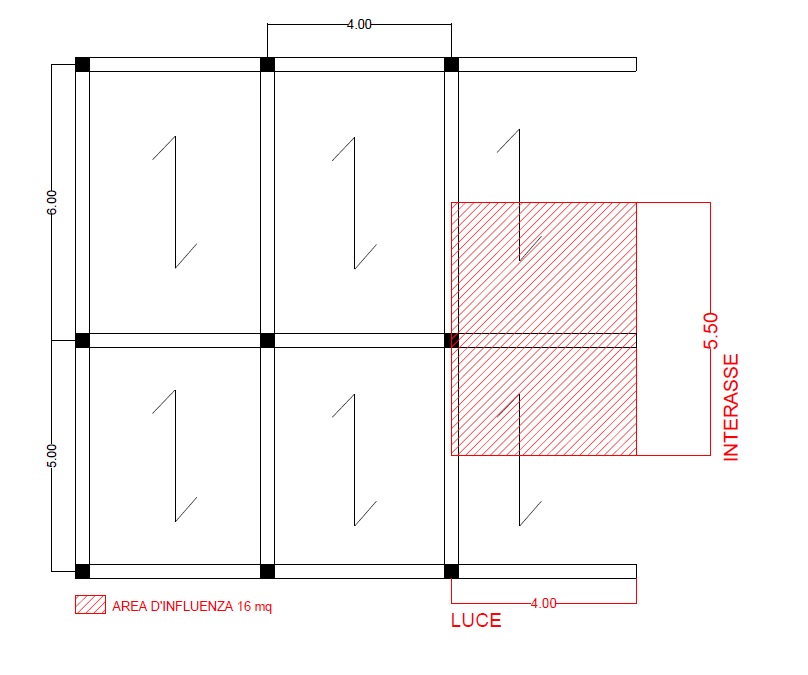
LUCE: 4.00 m

INTERASSE: 5.50 m

AREA: 22 MQ

 

DIMENSIONAMENTO TRAVE IN CALCESTRUZZO ARMATO

Come nella precedente esercitazione, vado a definire la sezione del solaio

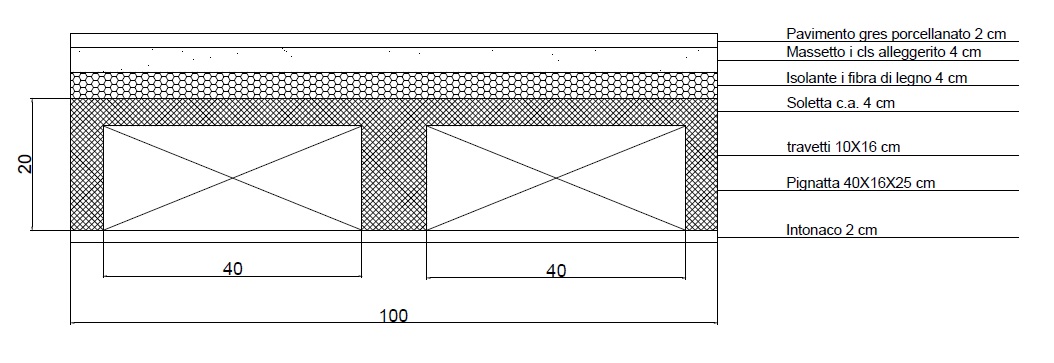
1) Sovraccarico strutturale: 

• peso pignatte: n°pignatte x peso singola pignatta (kg) ---> 2 x 8 kg = 16 kg = 0,16 KN
• peso travetti: volume (mc/mq) x peso specifico del cls (KN/mc) --->

(0,16 x 0,1 x 1) (mc/mq) x 25 KN/mc = 0,4 KN

• peso soletta:  0,04 m x 25 KN/mc = 1 KN/mc

Peso qs totale: 0,16 KN/mq + 0,4 KN/mq + 1 KN/mq = 1,56 KN/mc

 

2) Sovraccarico permanente:

• peso pavimento in gres porcellanato: spessore (m) x peso unitario (KN/mq) --->

 0,02 m x 20 KN/mq = 0,4 KN/mq

• peso massetto in cls alleggerito: spessore (m) x peso unitario (KN/mq) --->

0,04 m x 16 KN/mq = 0,64 KN/mq

• peso allettamento: spessore (m) x peso unitario (KN/mq) --->

0,02 m x 20 KN/mq = 0,4 KN/mq

• peso isolante in fibra di legno: spessore (m) x peso unitario (KN/mq) --->

0,04 m x 1 KN/mq = 0,04 KN/mq

• incidenza tramezzi: 1 KN/mq
• incidenza impianti: 0,5 KN/mq

Peso qp totale:

0,4 KN/mq + 0,64 KN/mq + 0,4 KN/mq + 0,04 KN/mq + 0,4 KN/mq + 1 KN/mq + 0,5 KN/mq = 3,38 KN/mq

3) Sovraccarico accidentale:

Da normativa, per edificio ad uso commerciale, qa = 4 KN/mq

4) carico totale distribuito sulla trave qu (KN/mq) = ( 1,3 x qs + 1,5 x qp + 1,5 x qa) x interasse

5) Inserisco i dati in Excel e noto che il primo dato che cambia rispetto all'esercitazione precedente è Mmax che, nel caso della mensola, è pari a ql²/2

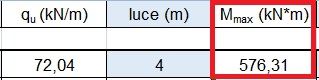
6) Definisco i materiali della mia trave e scelgo la classe di resistenza dell'acciaio e del calcestruzzo:

• classe di resistenza caratteristica dell'acciaio (fyk)  da armatura B450C che vale 450 MPa
• classe di resistenza del calcestruzzo (fck) per uso ordinario C34-35 che equivale a 35 MPa

In questo modo Excel calcola la tensione di progetto dell'acciaio (fyd), servendosi del coefficiente riduttivo per le resistenze a lunga durata acc = 0,85, e la tensione di progetto del calcestruzzo (fcd) servendosi del coefficiente parziale di sicurezza del calcestruzzo γc = 1,15

7) Fisso la base b= 30 cm; in questo modo ottengo un'altezza utile hu pari a 72,38 cm

Ottengo  Hmin= 77,38 cm aggiungendo il δ= 5 cm.  

Scelgo un H=80 cm affinché sia maggiore di Hmin. La trave non è verificata

8) Bisogna calcolare il peso proprio della trave e aggiungerlo ai carichi strutturali

Devo verificare che il rapporto tra la luce della mensola ed il suo spostamento sia maggiore di 250 come imposto dalla normativa. Per fare ciò, bisogna calcolare il momento di inerzia (b x h³)/12, bisogna ricalcolare il carico allo stato limite d’ esercizio[(Qs +Qp + 0.7 x Qa) x interasse] + peso della trave in c.a. ed infine lo spostamento verticale massimo della mensola che come sappiamo è (qL⁴)/8EI.

qe = (qs+qp+qa x ψ) x interasse x peso trave

Il rapporto L/Vmax è maggiore di 250 quindi la trave supera la prova a deformabilità a stato limite d’esercizio.

Aumentando la sezione della mia trave da H = 80 cm ad H= 85 il profilo è verificato.

 

DIMENSIONAMENTO TRAVE IN LEGNO

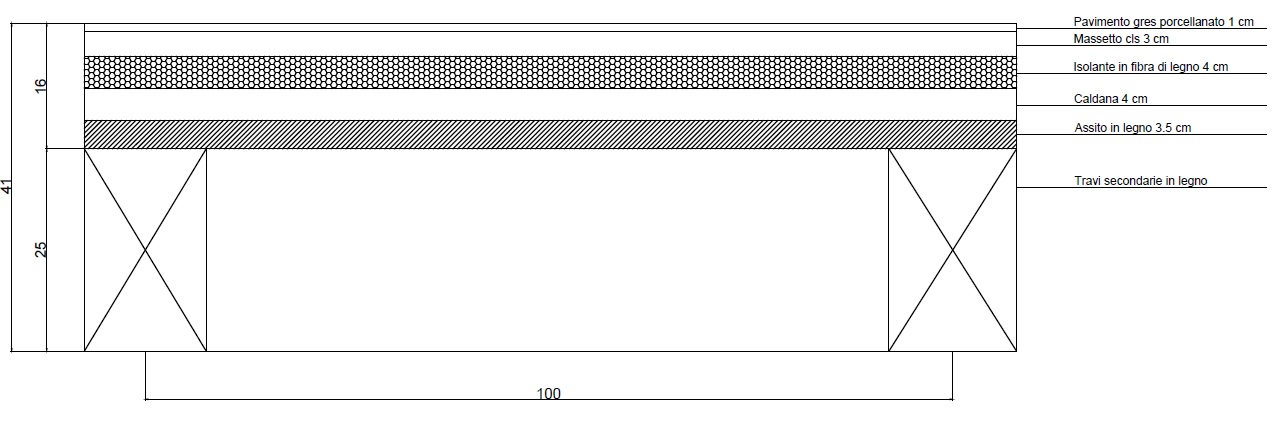
1) Sovraccarico strutturale

• peso tavolato in legno di rovere: volume (mc/mq) x peso specifico (KN/mq) --->

(0,035 x 1 x 1) (mc/mq) x 6,9 KN/mq = 0,24 KN/mq

• peso caldana in cls: spessore (m) x peso specifico (KN/mq) ---> 0,04 m x 25 KN/mq = 1 KN/mq
• peso del travetto: area (mq) x peso specifico (KN/mq) ---> 0,0375 mq x 6,9n KN/mc = 0,25 KN/mq

Peso qs totale:  0,24 KN/mq + 1 KN/mq + 0,25 KN/mq = 1,49 KN/mq

2) Sovraccarico permanente

• peso pavimento in marmo: spessore (m) x peso unitario (KN/mq) --->

0,02 m x 0,8 KN/mq = 0,016 KN/mq

• peso massetto in cls alleggerito: spessore (m) x peso unitario (KN/mq) --->

0,08 m x 18 KN/mq = 1,44 KN/mq

• peso isolante in fibra di legno: spessore (m) x peso unitario (KN/mq) --->

0,04 m x 1 KN/mq = 0,04 KN/mq

• incidenza tramezzi 1 KN/mq
• incidenza impianti 0,5 KN/mq

Peso qp totale:  0,016 KN/mq + 1,44 KN/mq + 0,03 KN/mq + 1 KN/mq + 0,5 KN/mq = 2,99 KN/mq

3) Sovraccarico accidentale

qa = 4 KN/mq

4) carico totale distribuito sulla trave qu (KN/mq) = ( 1,3 x qs + 1,5 x qp + 1,5 x qa) x interasse

5) Inserisco la Luce della trave per calcolare quanto vale il momento flettente massimo (Mmax) agente sulla trave (considerando la mia trave come una mensola quindi con un momento massimo pari a (ql²)/2)

6) Come tipologia di legno ho scelto il legno lamellare. Inserisco in Excel  la tensione caratteristica a flessione fmk del legno da me scelto che equivale a 24 MPa

7) Imposto la base b = 20 cm per ricavare l'altezza hmin, che mi permetterà di scegliere un’altezza di progetto H (maggiore di hmin). 

h min = 111,28

H = 115

8) Ora bisogna calcolare il peso proprio della trave e aggiungerlo ai carichi strutturali

Verifico che il rapporto tra la luce della mensola ed il suo spostamento sia maggiore di 250 come imposto dalla normativa. Per fare ciò:  momento di inerzia (b x h³)/12, bisogna ricalcolare il carico allo stato limite d’esercizio[(qs +qp + 0.7 x qa) x interasse]  ed infine lo spostamento verticale massimo della mensola che come sappiamo è (qL⁴)/8EI.

qe = (qs+qp+qa x ψ) x interasse

Il rapporto L/Vmax è maggiore di 250 quindi la trave supera la prova a deformabilità a stato limite d’esercizio.

 

DIMENSIONAMENTO TRAVE IN ACCIAIO

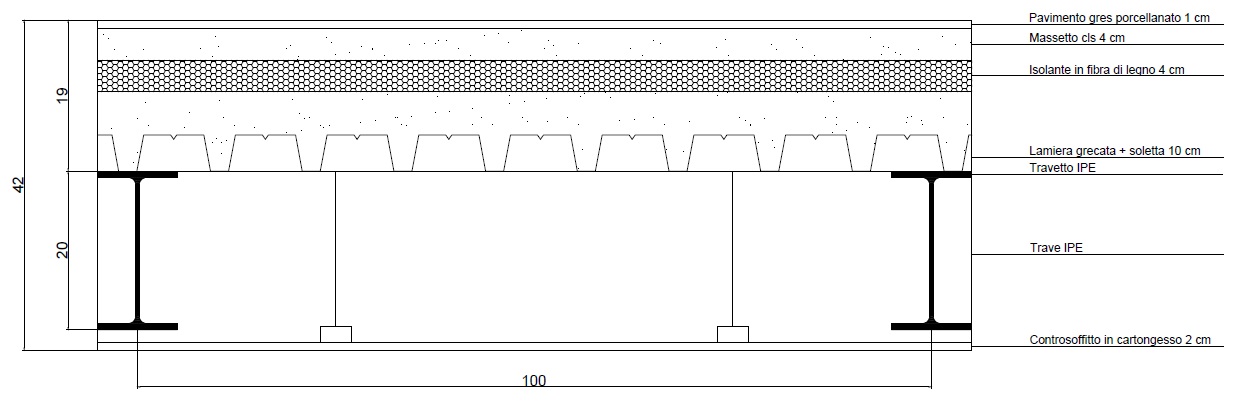
1) Sovraccarico strutturale

• peso lamiera grecata: spessore (m) x peso specifico (KN/mq) --->

0,08 m x 0,1 KN/mq = 0,008 KN/mq

• peso soletta: volume (mc/mq) x peso specifico (KN/mq) ---> 0,21 mc x 25 KN/mq = 5,25 KN/mq
• peso travetto IPE 140: 0,12 KN/mq

Peso qs totale: 0,008 KN/mq + 5,25 KN/mq + 0, 12 KN/mq = 5, 37 KN/mq

2) Sovraccarico permanente

• peso pavimento in marmo: spessore (m) x peso unitario (KN/mq) --->

0,02 m x 0,8 KN/mq = 0,016 KN/mq

• peso massetto in cls alleggerito: spessore (m) x peso unitario (KN/mq) --->

0,08 m x 18 KN/mq = 1,44 KN/mq

• peso isolante in fibra di legno: spessore (m) x peso unitario (KN/mq) --->

0,04 m x 1 KN/mq = 0,04 KN/mq

• incidenza tramezzi 1 KN/mq
• incidenza impianti 0,5 KN/mq

Peso qp totale:  0,016 KN/mq + 1,44 KN/mq + 0,03 KN/mq + 1 KN/mq + 0,5 KN/mq = 2,99 KN/mq

3) Sovraccarico accidentale

Da normativa, per edificio ad uso commerciale, qa = 4 KN/mq

4) Trovati qs, qp e qa, li inserisco nella tabella Excel e trovo il carico totale distribuito sulla trave qu (KN/mq) attraverso la somma dei carichi distribuiti aumentati ciascuno del loro coefficiente di sicurezza γ:

qu = ( 1,3 x qs + 1,5 x qp + 1,5 x qa) x interasse

5) Inserisco la Luce della trave per calcolare quanto vale il momento flettente massimo (Mmax) agente sulla trave (n.b. i pilastri vengono considerati come semplici appoggi quindi il modello sarà quello di una trave appoggiata appoggiata. Il momento massimo in mezzeria equivale a ql²/8)

6) Scelgo una delle tre classi di acciaio strutturale, nel mio caso S275  con la tensione caratteristica di snervamento pari a fyk = 275 MPa. Adesso ho trovato la tensione di progetto fd  dalla quale mi ricavo il modulo di resistenza minimo rispetto all'asse x  Wx,min = 734,39. Con questo parametro ricavo la sezione della trave IPE ( IPE 360)

7) Ora bisogna calcolare il peso proprio della trave e aggiungerlo ai carichi strutturali:

Momento di inerzia (b*h³)/12

Carico allo stato limite d’esercizio [(Qs +Qp + 0.5*Qa) * interasse] + peso della trave in acciaio

Spostamento verticale massimo della mensola (qL⁴)/8EI.

qe = (qs+qp+qa x ψ) x interasse x peso trave

Il rapporto L/Vmax è maggiore di 250 quindi la trave supera la prova a deformabilità a stato limite d’esercizio dopo aver scelto un profilo IPE 600 con Wx = 3069