Esercitazione III : Dimensionamento di una mensola in cls armato, acciaio, legno
La geometria che utilizzerò per il dimensionamento della mensola, nelle tre tecnologie: cls armato, acciaio e legno è la seguente
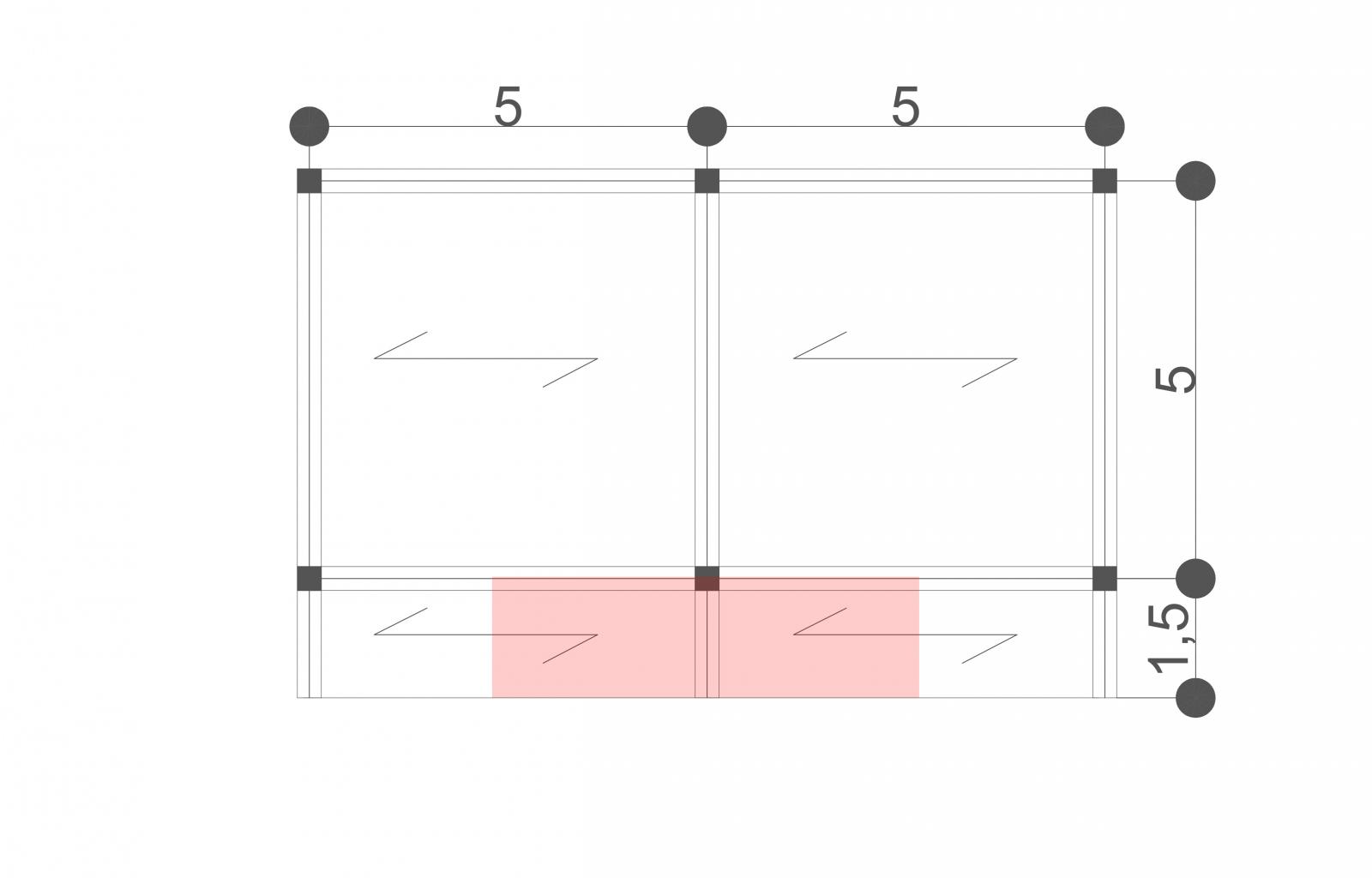
La trave maggiormente sollecitata ha una luce di 1,5m e un interasse di 5m
MENSOLA IN CLS ARMATO
Definisco la stratigrafia del mio solaio, in questo caso latero cementizio, e calcolo tutti i carichi che vi gravano, come nella precedente esercitazione.
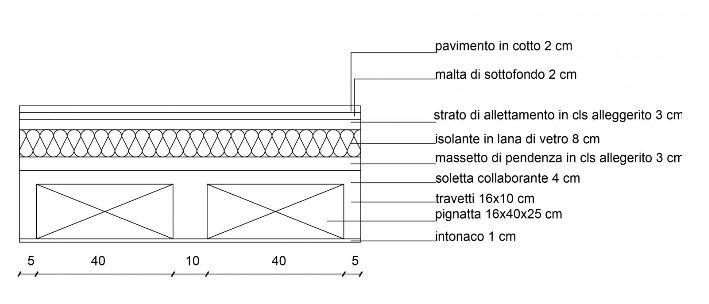
Carico strutturale (qs)
- soletta collaborante : (0,04m x 1m x 1m)/mq x 24KN/mc = 0,96 KN/mq
- travetti: 2(0,10m x 0,16m x 1m)/mq x 24KN/mc = 0,768 KN/mq
- pignatta: 8 x 9,1 Kg/mq = 72,8 Kg/mq = 0,728 KN/mq
Qs = (0,96 + 0,768 + 0,728 ) KN/mq = 2,456 KN/mq
Carico permanente (qp)
- pavimento in cotto: 24Kg/mq = 0,24KN/mq
- malta di sottofondo: (0,02m x 1m x 1m)/mq x 18KN/mc = 0,36KN/mq
- strato di allettamento in cls (0,03m x 1m x 1m)/mq x 24KN/mc= 0,72KN/mq
- isolante in lana di vetro (0,08m x 1m x 1m)/mq x 0,2KN/mc = 0,016KN/mq
- massetto delle pendenze (0,04m x 1m x 1m)/mq x 18KN/mc = 0,72KN/mq intonaco (0,01m x 1m x 1m)/mq x 13KN/mc = 0,13KN/mq
Qp= (0,24 + 0,36 + 0,72 + 0,016 + 0,72 + 0,13 ) KN/mq = 2,186 KN/mq
Carico accidentale (qa)
Anche qui ho ipotizzato un uso residenziale, seguendo la tabella della normativa quindi ho:
Qa = 2 KN/mq
Dopo aver inserito nel file anche la luce, viene calcolato automaticamente il Mmax agente sulla trave.
In seguito imposto le proprietà sia dell’acciaio (fyk) che del calcestruzzo (fck) che vengono automaticamente moltiplicati per i loro coefficienti di sicurezza (1,15 e 1,5).
Essendo la trave composta da due materiali diversi, le proprietà del materiale devono essere omogenizzate secondo un coefficiente (n=15) in modo da ottenere ß e r.
Ora posso impostare la larghezza della trave (b=40 cm) così che Excel mi calcola l’altezza utile della trave (Hu=21,38), che sommata alla distanza dal baricentro del ferro teso al lembo teso (δ=4) e mi da l’altezza minima(Hmin=25,38).
Ingegnerizzo scegliendo una sezione alta 30 cm.
A questo punto è possibile ottenere il peso unitario della trave e il Qe;
Automaticamente quindi Excel svolge un’altra volta tutta la riga con i nuovi dati (è cambiato il qu) così posso sapere se la trave progettata è verificata o meno.
È verificata
Il procedimento per il dimensionamento della mensola è molto simile a quello per la trave doppiamente appoggiata, ma in più anche per il cemento armato sarà necessario fare la verifica ad abbassamento dove Vmax=qel^4/8EIx e l/ Vmax ≥ 250
MENSOLA IN ACCIAIO
Carico strutturale (qs)
- IPE 200: 2 (0,00285 mq x 1 m) / 78,5 KN/mc = 0,447 KN/mq
- Getto in calcestruzzo e lamiera grecata: (21 kN/mc x 0,075 mc) / 1 mq = 1,86 KN/mq
Qs = 0,447 kN/mq + 1,86 kN/mq = 2,307 kN/mq
Carico permanente (qp)
-pavimento, 0,3 KN/mq
-massetto, (0,03 m x 1 m x 1 m) /mq x 19 KN/mc = 0,57 KN/mq
-isolante, (0,06 m x 1 m x 1 m) /mq x 14 Kn/mc = 0,84 KN/mq
Qp = 0,3 KN/mq + 0,57 KN/mq + 0,84 KN/mq = 1,71 KN/mq
Carico accidentale (qa)
Anche qui ho ipotizzato un uso residenziale, seguendo la tabella della normativa quindi ho:
Qa = 2 KN/mq
Compilo il foglio Excel con i tre carichi così da calcolare il qu.
In seguito aggiungo la luce della trave (3m) così da ottenere il Mmax (M =ql^2/2)
Aggiungo le caratteristiche del materiale fyk che verrà moltiplicato per il coefficiente di sicurezza γ=1,05 per ottenere il Wxmin (215,24).
Dato Wxmin, scelgo sul sagomario un'IPE 220 e di conseguenza inserisco il valore del momento di inerzia in tabella Ix=2772cm^4
Con questi ultimi dati posso verificare se la sezione scelta rispetta i limiti di abbassamento. Il foglio infatti mi calcolerà il Qe (che in questo caso tiene in considerazione anche il peso della trave, a differenza del legno che è considerato un materiale leggero ), con cui sarà possibile calcolare l'abbassamento max (Vmax) e verificare che il rapporto tra la luce della trave e il suo spostamento max sia maggiore di 250, come da normativa.
Vmax=qel^4/8EIx l/ Vmax ≥ 250
la sezione è verificata ed idonea
MENSOLA IN LEGNO
Carico strutturale (qs)
-tavolato, (0,03 m x 1 m x 1 m) /mq x 7 KN/mc = 0,21 KN/mq
-travetti, 2(0,1 m x 0,14 m x1 m) /mq 6 KN/mq = 0,168 KN/mq
Qs = 0,21 KN/mq + 0,168 KN/mq = 0,378 KN/mq
Carico portato (qp)
-pavimento, 0,3 KN/mq
-massetto, (0,03 m x 1 m x 1 m) /mq x 19 KN/mc = 0,57 KN/mq
-allettamento, (0,06 m x 1 m x 1 m) /mq x 14 Kn/mc = 0,84 KN/mq
Qp = 0,3 KN/mq + 0,57 KN/mq + 0,84 KN/mq = 1,71 KN/mq
Carico accidentale (qa)
Prendendo la tabella dalla normativa ho ipotizzato un uso residenziale quindi ho:
Qa = 2 KN/mq
Compilo il foglio Excel con i tre carichi così da calcolare il qu, che è la somma dei tre carichi moltiplicati per dei coefficienti di sicurezza x l’interasse.
In seguito posso aggiungere la luce della trave, in modo da ottenere il Mmax.
Fino a questo punto il l’iter di progetto utilizzato è lo stesso per quella della trave doppiamente appoggiata, ma il Mmax è differente poiché dobbiamo far riferimento al modello di mensola, quindi
M =ql^2/2
Inserisco i dati relativi al tipo di legno scelto per la trave da progettare.
Imposto una base di 30 cm ottenendo una Hmin pari a 20,14.
Ingegnerizzo questa misura prendendo H = 25 cm
Per la mensola è necessario calcolare e verificare l’abbassamento della trave.
Determino quindi il modulo elastico (E=8000) e il momento d'inerzia (Ix=(b*h³) /12) e carico totale qe (combinazione di carico frequente per SLE reversibili), necessario per il calcolo dello spostamento.
Qe = (G1 + G2 + Ψ1 x Q1) x i
A questo punto è possibile calcolare l'abbassamento max (Vmax) e verificare che il rapporto tra la luce della trave e il suo spostamento max sia maggiore di 250, come da normativa.
Vmax=qel^4/8EIx l/ Vmax ≥ 250
E' Verificata


Commenti recenti