Esercitazione1: Predimensionamento e verifica di un telaio in acciaio, legno, calcestruzzo armato

Esercitazione realizzata da Rebecca Brock e Francesca Di Gregorio.

Abbiamo scelto un unico telaio per tutte e tre le differenti tecnologie:

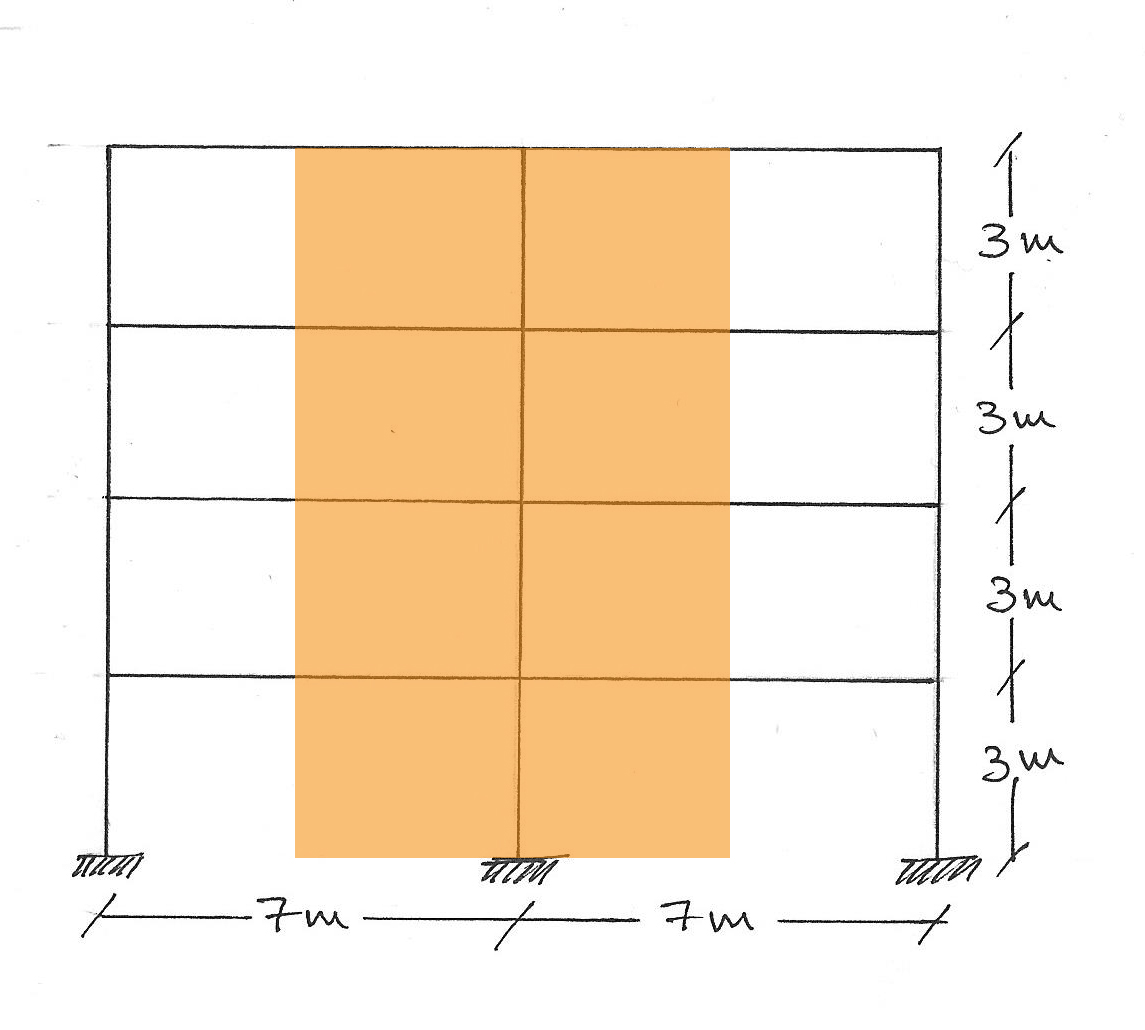
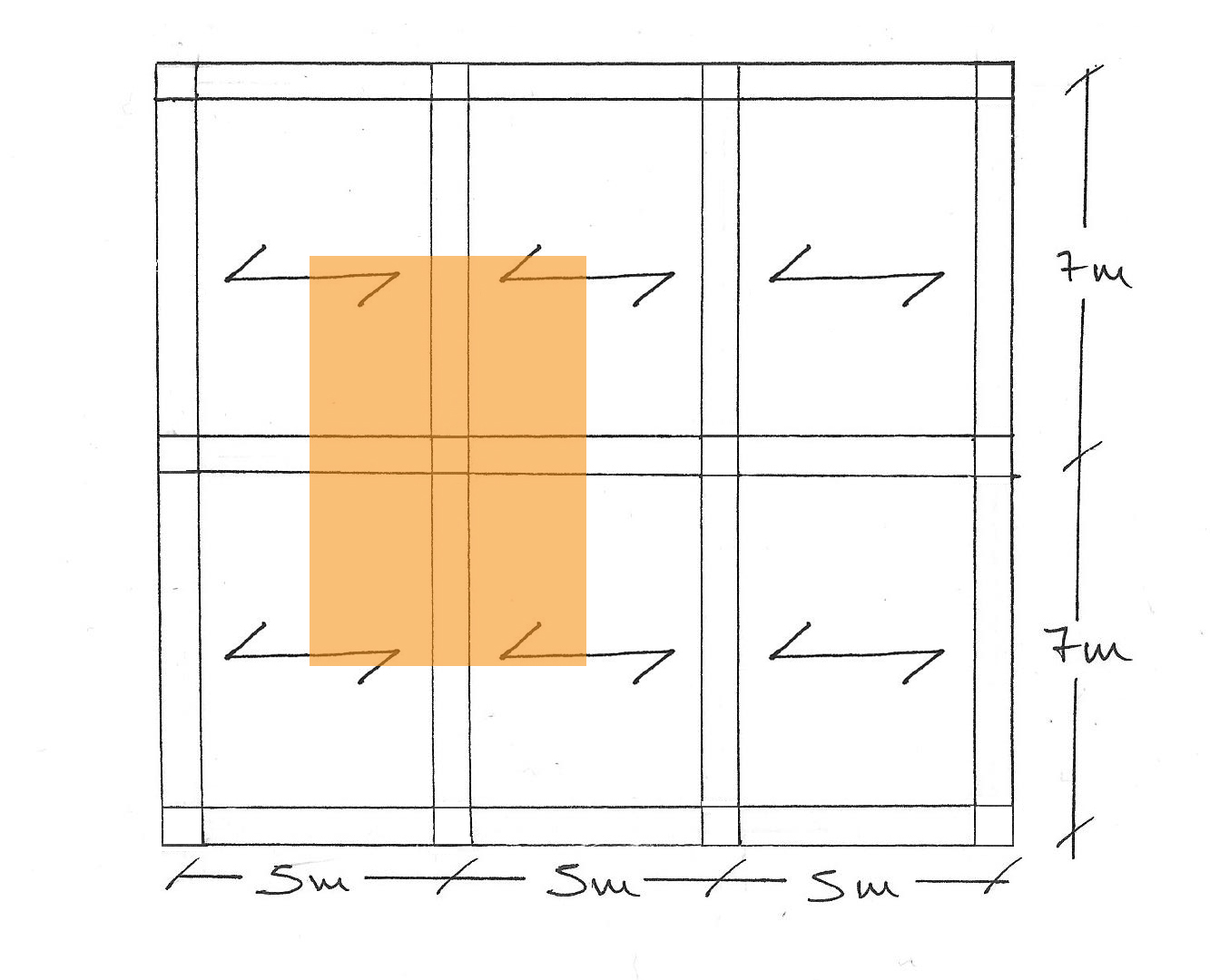
ACCIAIO:

- Analisi dei carichi:

Qs: carico strutturale

• lamiera grecata + soletta = 1,65 kN/m²
• IPE 140 γ = 12,9 kN/m³, interasse = 2,3 m

Qs = 1,65 + (12,9 x 1/2,3) = 1,704 kN/m² 

Qp: carico permanente

• isolante termico γ = 7,97 kN/m³
• massetto γ = 21 kN/m³ 
• pavimentazione parquet γ = 7,2 kN/m³ 
• impianti 0,5 kN/m
• tramezzi 1 kN/m

Qp = (0,04 x 7,97) + (0,05 x 21) + (0,02 x 7,2) + 0,5 + 1 = 3,0128 kN/m²

Qa: carico accidentale

Qa = 2 kN/m²

- Dimensionamento travi

Su un foglio di calcolo Excel abbiamo inserito i valori trovati e calcolato la combinazione di carico al metro lineare. Poiché la struttura è iperstatica, abbiamo individuato il momento massimo, M_max, come se fosse una trave appoggiata-appoggiata (M=ql²/8). Stabilita la tensione di snervamento caratteristica f_yk e trovata la tensione di progetto f_yd, abbiamo individuato il modulo di resistenza a flessione minimo (W_x,min) e di conseguenza la sezione IPE.

- Dimensionamento pilastri

Per il predimensionamento dei pilastri abbiamo individuato l'area di influenza del pilastro più sollecitato e il carico agente su esso (peso del solaio e peso delle porzioni di travi portate). Da esso abbiamo calcolato lo sforzo normale massimo portato dal pilastro a terra.

Dallo sforzo nomale massimo (N_max) e dalla tensione di progetto (f_cd) abbiamo ricavato la sezione minima. Usando la luce libera di inflessione (l₀xβ) e il modulo di elasticità, abbiamo trovato la snellezza (λ) e da essa il valore minimo del raggio di inerzia minimo (ρ_min), necessario per evitare l'instabilità eulariana. Tenendo conto di A_min e ρ_min abbiamo scelto la sezione HE idonea.

Poiché per il dimensionamento della struttura sono state calcolate e sollecitazioni come se essa fosse isostatica, per la verifica è stato necessatio introddurre il telaio su SAP2000 per ricalcolare correttamente le sollecitazioni della struttura iperstatica.

- Analisi SAP 2000

- Verifica trave

σ = M/W < fd

Con i valori ottenuti da SAP abbiamo verificato che la tensione ottenuta (σ=M/W) fosse minore di quella di progetto (f_d). Poiché essa risultava notevolmente minore di quella progettata, abbiamo diminuito la sezione, scegliendo una sezione IPE più piccola che si avvicinasse maggiormente alla tensione ottenuta.

- Verifica pilastro

σ = N/A + M/W < fd

Confrontando la tensione ottenuta da SAP, la sezione del pilastro non risultava verificata (la tensione ottenuta era molto maggiore di quella di progetto), così abbiamo gradualmente modificato la sezione scegliendo profilati HE più grandi, fino ad ottenerne uno che risultava idoneo.

LEGNO:

- Analisi dei carichi:

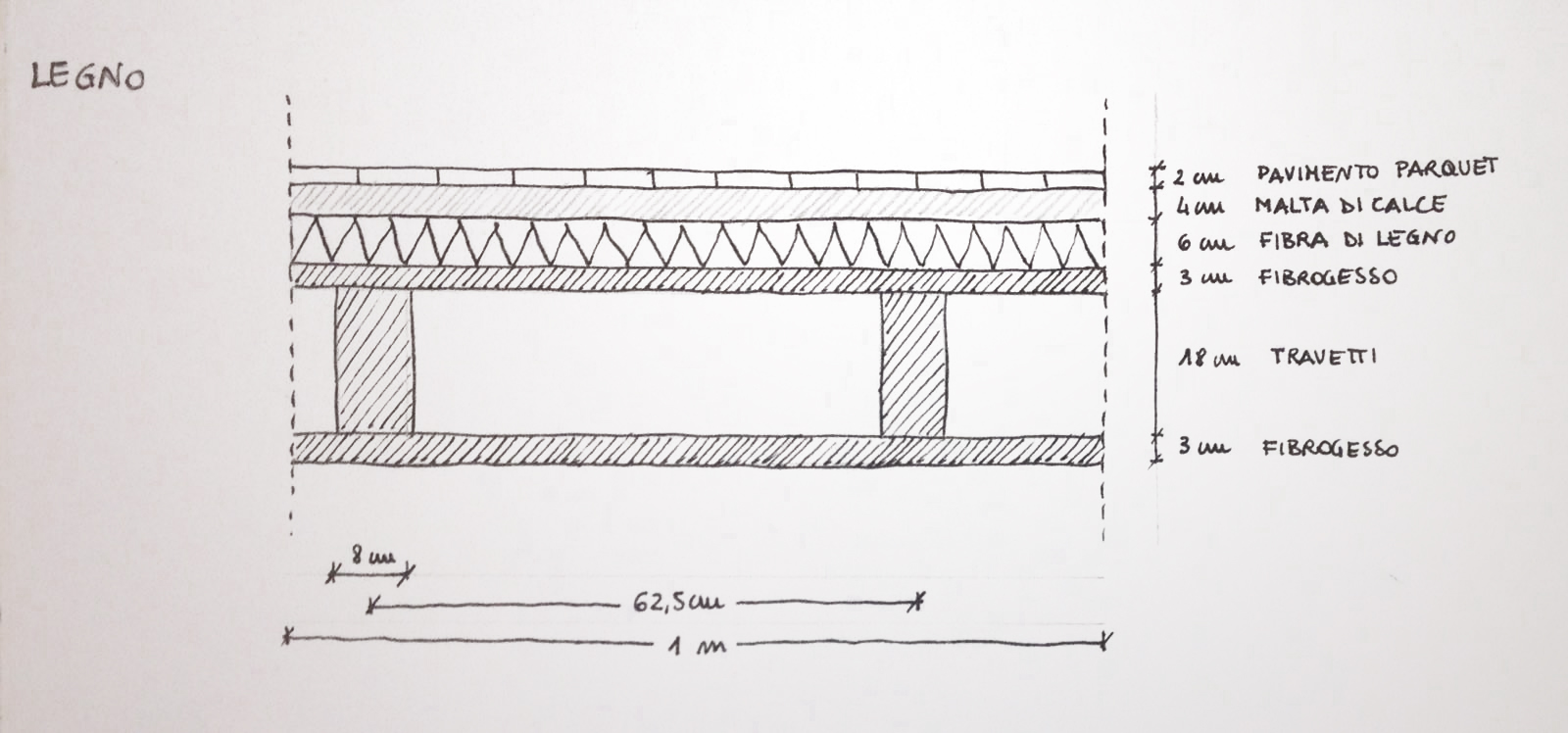
Qs: carico strutturale

• fibrogesso γ = 11,5 kN/m³
• travetto legno lamellare γ = 3,8 kN/m³, interasse = 0,625 m

Qs = (11,5 x 0,03)x2 + (0,08 x 0,18 x 3,8 x 1/0,625) =  0,778 kN/m² 

Qp: carico permanente

• fibra di legno γ = 2,1 kN/m³
• malta di calce γ = 18 kN/m³ 
• pavimentazione parquet γ = 7,2 kN/m³ 
• impianti 0,5 kN/m
• tramezzi 1 kN/m

Qp = (0,06 x 2,1) + (0,054x 18) + (0,02 x 7,2) + 0,5 + 1 = 2,616 kN/m²

Qa: carico accidentale

Qa = 2 kN/m²

- Dimensionamento travi

Come per l'acciaio, abbiamo calcolato il momento massimo agente sulla trave. Dividendo quest'ultimo (M_max) per la tensione di progetto (f_d) abbiamo ricavato il modulo di resistenza a flessione minimo (W_x,min). Fissata la base, abbiamo ottenuto l'altezza minima necessaria a contrastare il momento, h=(6W/b)^1/2. Da questo valore abbiamo ricavato l'altezza della trave.

- Dimensionamento pilastri

E' stato calcolato lo sforzo normale portato a terra dal pilastro.

Dallo sforzo nomale massimo (N_max) e dalla tensione di progetto (f_cd) abbiamo ricavato la area di sezione minima. Usando la luce libera di inflessione (l₀xβ) e il modulo di elasticità, abbiamo trovato la snellezza (λ) e da essa il valore minimo del raggio di inerzia minimo (ρ_min) necessario per evitare l'instabilità eulariana. Da ρ_min abbiamo individuato la base, b=ρx12^1/2, e l'altezza minima, dalle quali abbiamo definito le dimensioni della sezione.

Poiché per il dimensionamento della struttura sono state calcolate e sollecitazioni come se essa fosse isostatica, per la verifica è stato necessatio introddurre il telaio su SAP2000 per ricalcolare correttamente le sollecitazioni della struttura iperstatica.

- Analisi SAP 2000

- Verifica trave

Con i valori ottenuti da SAP abbiamo verificato che la tensione ottenuta (σ=M/W) fosse minore di quella di progetto (f_d), come risulta.

- Verifica pilastro

Confrontando la tensione ottenuta da SAP, la sezione del pilastro non risultava verificata, così abbiamo modificato le dimensioni della sezione, ottenendo un valore della tensione più idoneo.

CALCESTRUZZO:

- Analisi dei carichi:

Qs: carico strutturale

• pignatta γ = 12 kN/m³
• calcestruzzo γ = 25 kN/m³, interasse = 0,5 m

Qs = (0,04 x 25) + (0,1 x 0,16 x 25) x 2 + (0,4 x 0,16 x 12) x 2 = 3,336 kN/m² 

Qp: carico permanente

• massetto γ = 18 kN/m³ 
• isolante acustico γ = 1 kN/m³ 
• pavimentazione cotto γ = 0,36 kN/m³ 
• impianti 0,5 kN/m
• tramezzi 1 kN/m

Qp = (0,04 x 18) + (0,013 x 1) + (0,025 x 0,36) + 0,5 + 1 = 1,86 kN/m²

Qa: carico accidentale

Qa = 2 kN/m²

- Dimensionamento travi

Come per il legno, abbiamo calcolato il momento massimo agente sulla trave. Quest'ultimo (M_max) è stato utilizzato per trovare l'altezza utile della trave, calcolata hu= r*(Mmax/b*fcd)^0.5, fissando precedentemente la base. Sommando questo valore al valore del copriferro è stata determinata l'altezza minima (hmin), successivamente ingegnerizzata. Trovata l'area della trave è stato calcolato il suo peso unitario ed è stato aggiunto questo valore al carico ultimo (qu). Il calcolo del peso proprio serve a capire se la base e l'altezza ingegnerizzata della propria trave resisterebbero anche sommando al carico ultimo il peso della stessa trave.

- Dimensionamento pilastri

E' stato calcolato lo sforzo normale portato a terra dal pilastro.

Dallo sforzo nomale massimo (N_max) e dalla tensione di progetto (f_cd) abbiamo ricavato la area di sezione minima. Usando la luce libera di inflessione (l₀xβ) e il modulo di elasticità, abbiamo trovato la snellezza (λ) e da essa il valore minimo del raggio di inerzia minimo (ρ_min) necessario per evitare l'instabilità eulariana. Da ρ_min abbiamo individuato la base, b=ρx12^1/2, e l'altezza minima, dalle quali abbiamo definito le dimensioni della sezione.

Poiché per il dimensionamento della struttura sono state calcolate e sollecitazioni come se essa fosse isostatica, per la verifica è stato necessatio introddurre il telaio su SAP2000 per ricalcolare correttamente le sollecitazioni della struttura iperstatica.

- Analisi SAP 2000

- Verifica trave

Con i valori ottenuti da SAP abbiamo verificato che la tensione ottenuta (σ=M/W) fosse minore di quella di progetto (f_d), come risulta.

- Verifica pilastro

Allo stesso modo risulta idonea la sezione scelta precedentemente in quanto la tensione ottenuta risulta minore rispetto a quella di progetto.