11 CLICK

Metodo delle Forze

1_Utilizzando il metodo delle forze si può risolvere un qualsiasi tipo di struttura iperstatica, riconducendoci a strutture semplicissime, passando da una struttura iperstatica a strutture isostatiche equivalenti.
2_ Nel caso di una struttura simmetrica per geometria, carico e vincoli, posso procedere ad analizzarla considerando solo una porzione.
3_ Per ottenere questo passaggio di tipologia strutturale, bisogna declassare uno o più vincoli a seconda di quante volte la prima struttura è iperstatica, senza però dimenticare di introdurre la cinematica relativa al vincolo dell'iperstatica poichè, se omessa, non risulterebbe equivalente al vincolo di partenza.
4_Ottengo coì un'incognita iperstatica X (forza generalizzata) e una struttura che presenta contemporanemente fozse isostatiche e iperstatiche (forze interne/esterne e agenti/reagenti): questo fa si che si avrà bisogno di un numero di equazioni di carattere cinematico ( relative agli spostamenti) pari al numero di vincolo, in qaunto si deve trovare la perfetta equivalenza tra le due strutture.
5_Queste equazioni ci consentiranno di trovare le incognite iperstatiche X per l'equivalenza tra gli schemi e rappresentano due forze uguali e opposte come forze interne/azioni di contatto e forze esterne.
6_Consideriamo ad esempio questa trave, messa a confronto con il suo schema equivalente

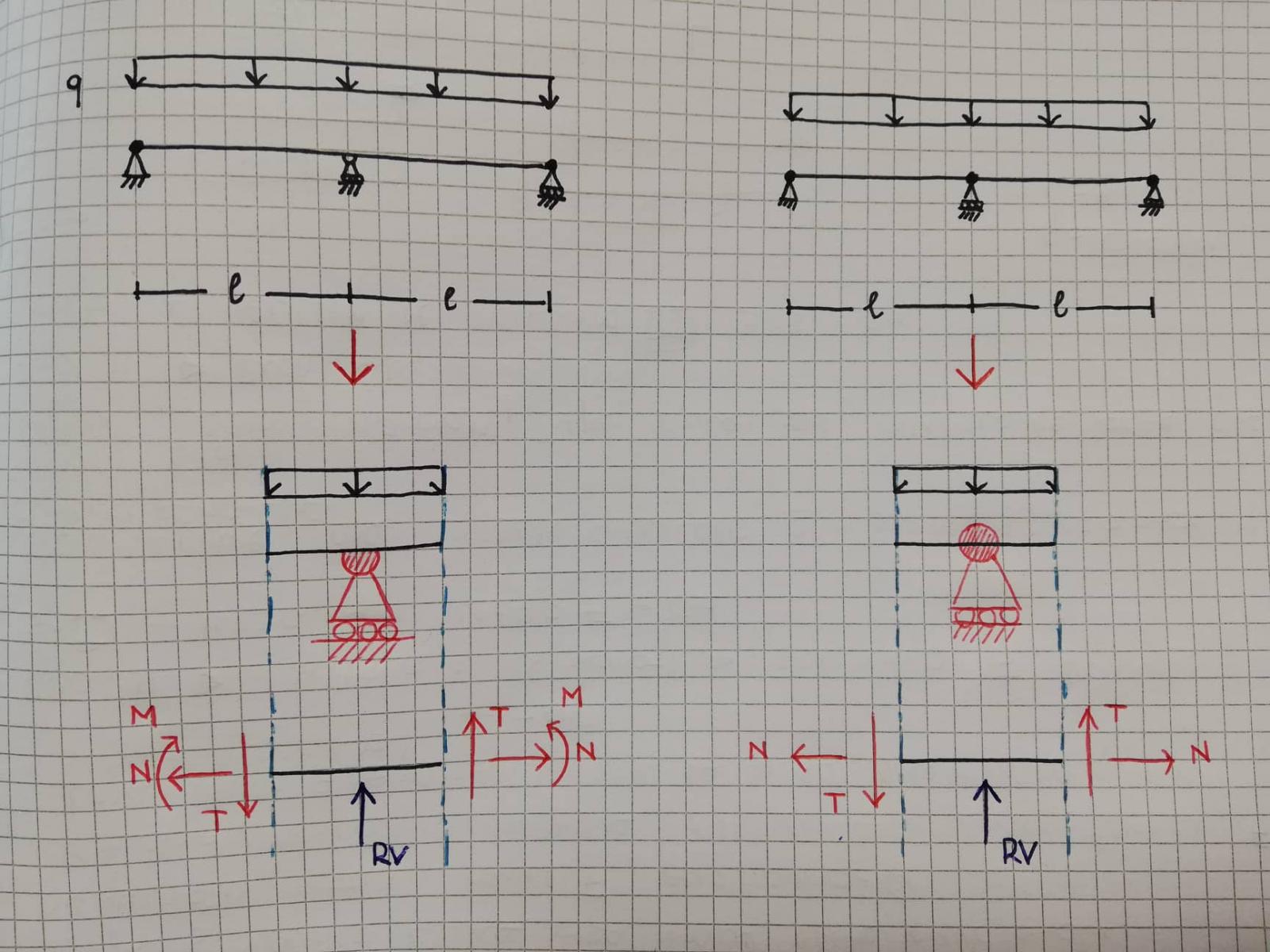
Il carrello presente in mezzeria nella prima struttura iperstatica è passante, ciò permette di mantenere la continuità nella trave e nelle forze generale; la seconda struttura, quella "equivalente" presenta un carrello con cerniera che invece frammenta in due porzioni la struttura, spezzando la continuità della trave. 
7_Eseguendo i tagli alla Cauchy e analizzando le sezioni dello schema in mezzeria possiamo vedere i diversi comportamenti che hanno i due vincoli sulla stessa trave: le due strutture non si equivalgono poichè la struttura di partenza, iperstatica, non trova la sua continuità nella struttura equivalente.
8_Lo schema iperstatico implica che tutte le forze di contatto si trasferiscano su tutta la lunghezza della trave; nello schema isostatico questa continuità viene bloccata dalla presenza della cerniera interna che, oltre a generare due tratti (destro e sinistro rispetto il vincolo di mezzeria), impedisce la trasmissione della continuità del momento.
9_Devo quindi aggiungere una coppia di forze intorno al vincolo della struttura isostatica (cerniera interna) che mi garantirà di determinare l'incognita iperstatica prima citata.

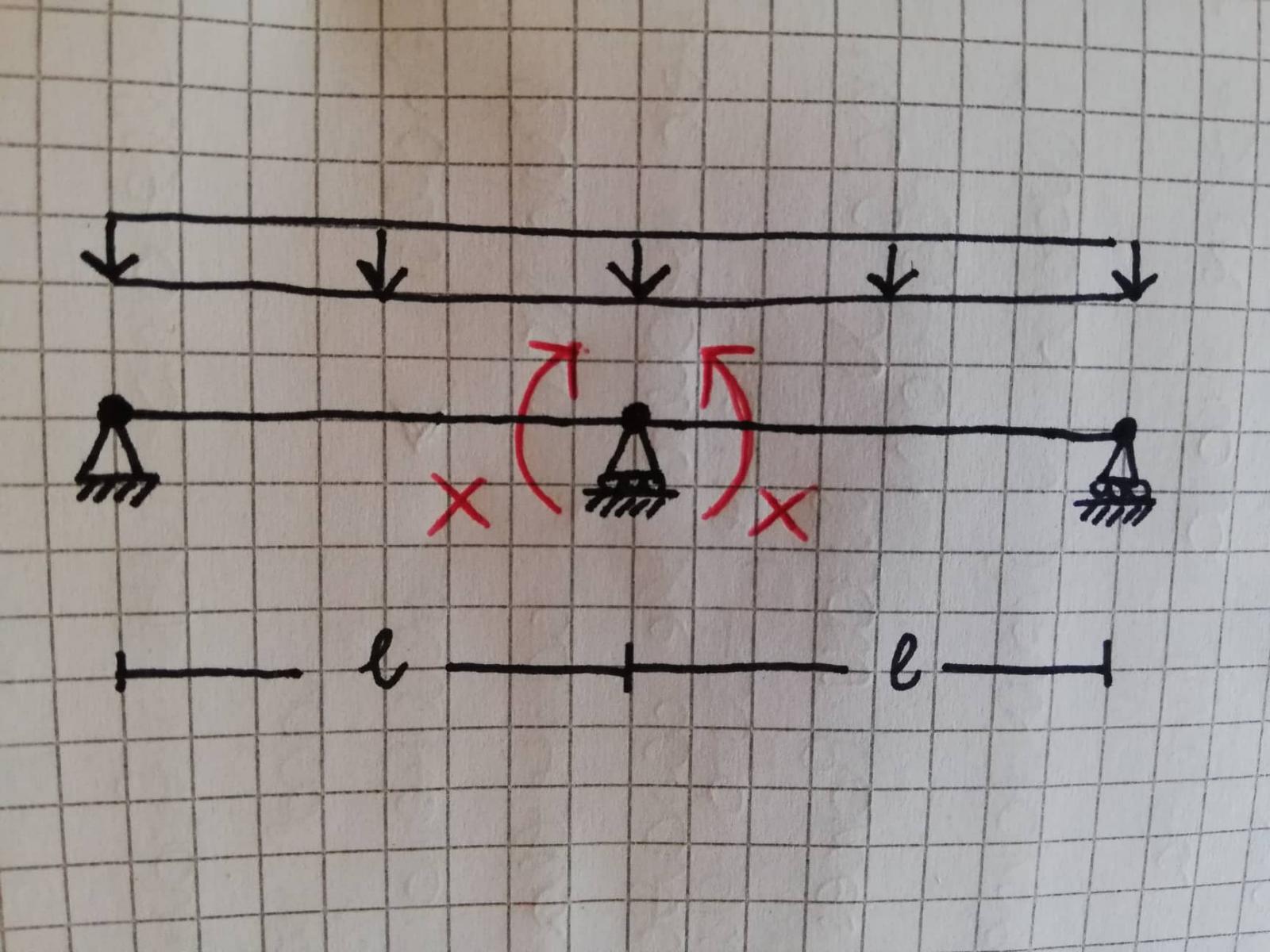
10_ Dovendo arrivare ad una equivalenza allora devo considerare l'elemento come unico (basandomi sulla struttura iniziale di carattere iperstatico) e cercare una continuità in termini cinematici:

• lo spostamento orizzontale di destra è uguale a quello di sinistra
  Ubs=Ubd, ovvero che Ubs - Ubd = 0 (traslazione orizzontale relativa è nulla)
• lo spostamento trasversale di sinistra è uguale a quello di destra
  Vbs=Vbd, ovvero che Vbs - Vbd = 0
• la terza relazione che dobbiamo imporre è che la rotazione nel vincolo B deve essere = 0, il che si traduce che l'equazione della rotazione a destra e a sinistra devono essere = 0 per la continuità della struttura, ma avendo una cerniera interna si può generare una rotazione relativa

11_All'incognita iperstatica stabilita come momento di contatto bisogna associare l'equazione cinematica relativa allo spostamento a cui questa incognita si oppone e che è quindi in grado di rigenerare l'effetto del vincolo di partenza. E' proprio per questo che impongo la rotazione relativa = 0

12_Proprio con questa equazione posso determinare il valore dell'incognita X posta in partenza, in modo da poter risolvere la struttura isostatica, ora equivalente alla struttura iperstatica iniziale.