ESERCITAZIONE III - Dimensionamento di un graticcio di travi inflesse in c.a
Studenti: Jacopo Sforza, Brooke Sison, Andrea Spinaci
INTRODUZIONE
Nella seguente esercitazione verrà analizzato il comportamento di un graticcio di travi inflesse in c.a. avente dimensioni 40 x 40 m appoggiato su pilastri posizionati lungo il perimetro di altezza 4 m e ipotizzando 3 piani superiori. Al fine di semplificare la progettazione della sezione delle travi che lo compongono utilizzeremo il modello di piastra che è un modello meccanico bidimensionale di un corpo reale tridimensionale che presenta due dimensioni, lungo le direzioni x e y, che sono molto superiori rispetto alla terza dimensione definita dallo spessore lungo la direzione z e i carichi che agiscono su di essa sono perpendicolari rispetto il piano medio.
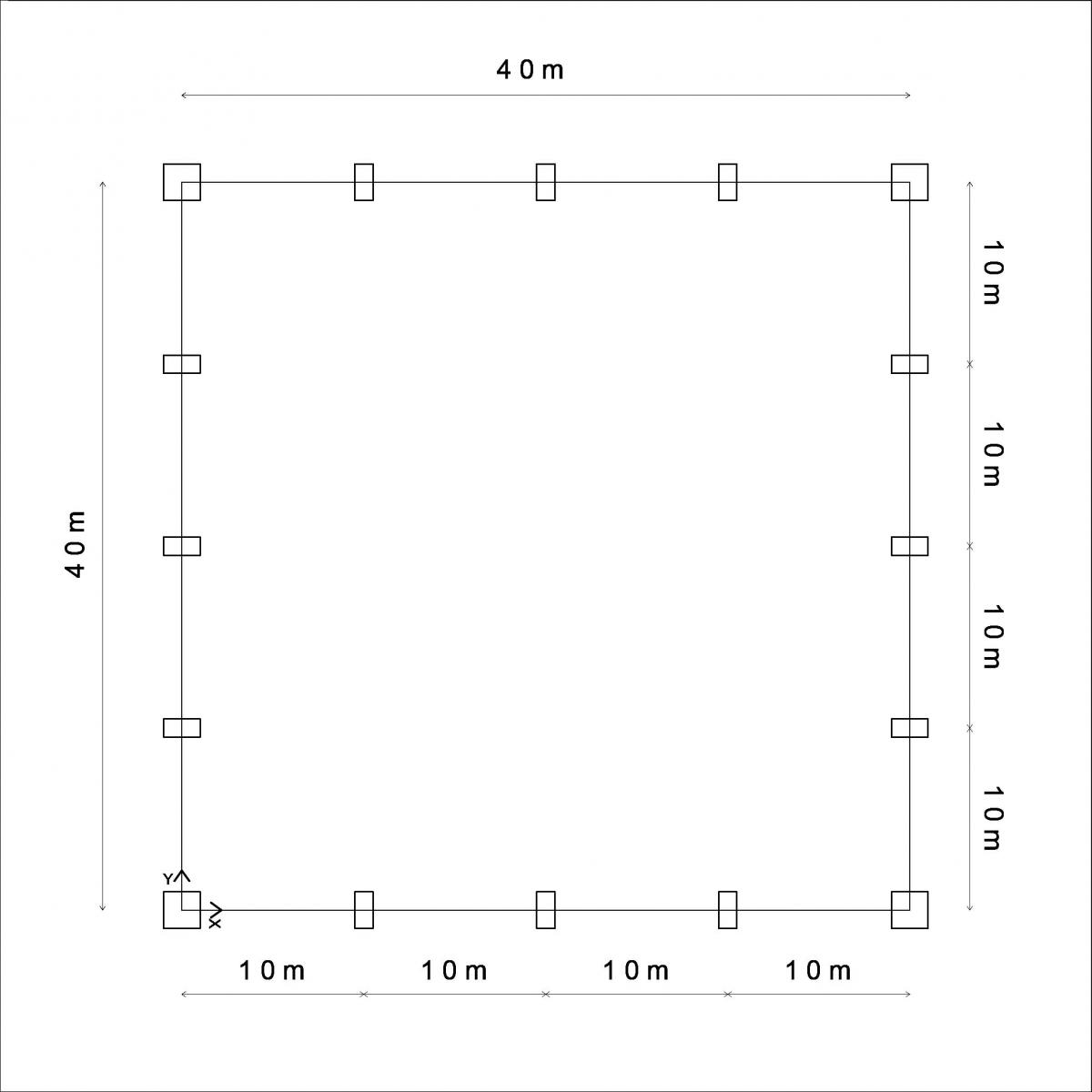
ANALISI DEI CARICHI
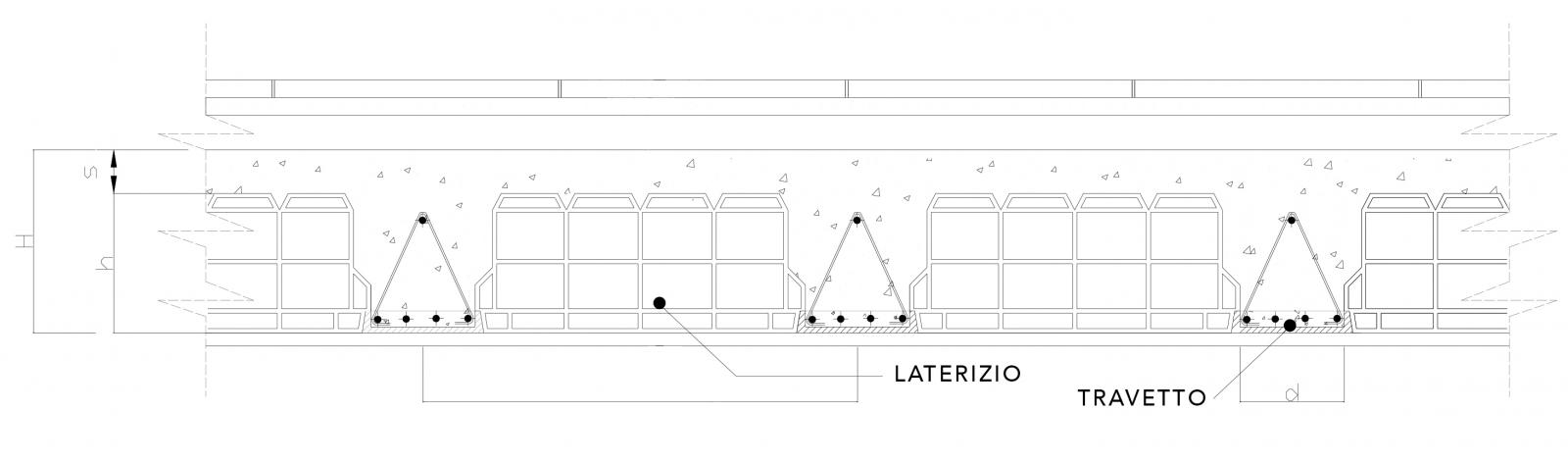
Successivamente è stata svolta l’analisi dei carichi del solaio in laterocemento dell'edificio sorretto dal graticcio. Vengono calcolati i diversi carichi agenti su un metro quadrato di solaio secondo tre categorie
- Qs = Carichi permanenti strutturali
- Qp = Sovraccarichi permanenti non strutturale
- Qa = Carichi accidentali
Con l’utilizzo del solaio in latero-cemento abbiamo considerato:
- carico strutturale permanente (Qs) = la somma dei pesi propri di tutti quegli elementi che costituiscono la struttura permanente del solaio: i travetti, le pignatte e la soletta collaborante.
- carico permanente non strutturale (Qp) = abbiamo considerato tutti quei elementi che sono posizionati sopra al pacchetto strutturale permanente: la pavimentazione in legno, allettamento + massetto porta impianti, l’isolante acustico, l'intonaco in gesso e l'incidenza dei tramezzi.
- carico accidentale (Qa) = definito dalla normativa in base alla destinazione d'uso, che in questo caso essendo a destinazione d’uso residenziale corrisponde a 2 KN/m2
Analisi dei carichi di un solaio in laterocemento (Qs)
Pignatte 50,00 cm = 0,50 m Peso specifico = 7,5 KN/m3
Soletta collaborante 4,00 cm = 0,04 m
Travetti x cm = x m Peso specifico = 25 KN/m3
Calcolo del carico distribuito superficiale (Qp)
Pavimento in legno 0,50 KN/m2
Isolante acustico 0,02 KN/m2
Allettamento + massetto 2,00 KN/m2
Intonaco in gesso 0,27 KN/m2
Tramezzi 1,60 KN/m2
Carico SLU
A questo punto abbiamo considerato le combinazioni di carico fornite dalla normativa per le verifiche allo stato limite, utilizzando coefficienti parziali di sicurezza sfavorevoli.
Combinazione di carico allo stato limite ultimo SLU:
Qu = γs Qs + γp Qp + γa Qa = 1,30 x 2,832 KN/m2 + 1,50 x 4,39 KN/m2 + 1,50 x 2,00 KN/m2 = 13,872 KN/m2
Combinazione di carico allo stato limite d’esercizio SLE
Questo valore di carico allo stato limite di esercizio ci servirà per le verifiche agli abbassamenti.
Qe = γs Qs + γp Qp + γa Qa = 1,00 x 2,832 KN/m2 + 0,70 x 4,39 KN/m2 + 0,70 x 2,00 KN/m2 = 7,305 KN/m2
Una volta ottenuto il valore della combinazione di carico agli stati limite, essendo un valore distribuito sulla superficie, abbiamo moltiplicato il valore per le dimensioni della piastra e moltiplicando per il numero di piani, ottenendo così il valore della forza concentrata equivalente al carico dovuto ai tre piani.
Forza concentrata SLE
40,00 m x 40,00 m x 7,305 KN/m2 x 3 piani = 35064 KN
Forza concentrata SLU
40,00 m x 40,00 m x 13,872 KN/m2 x 3 piani = 66585,6 KN
MODELLAZIONE SU SAP2000
Definita la geometria principale, abbiamo cominciato a modellare la struttura su SAP.
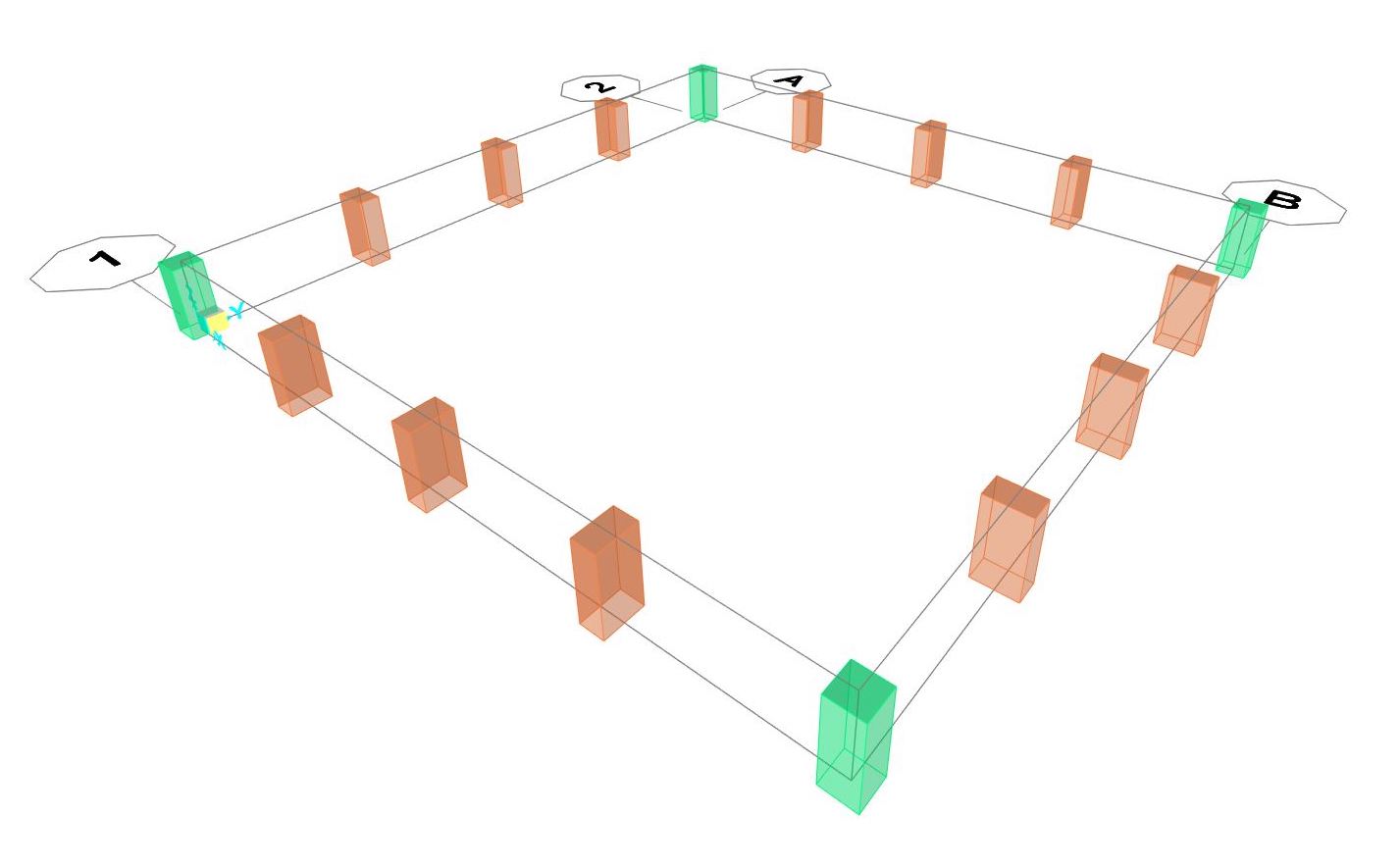
Viene inizialmente definita la dimensione > Grid Only 40 x 40 metri con h pilastri 4 metri. In seguito è stato definito il materiale: calcestruzzo ad alte prestazioni (C50/60) essendo il graticcio una morfologia molto complessa e impegnativa dal punto di vista strutturale. Define > Materials> Add New Material> Concrete> C50/60.
Oltre a definire il materiali sono state definite le diverse sezioni Define> Frame Sections> Rectangular>Concrete:
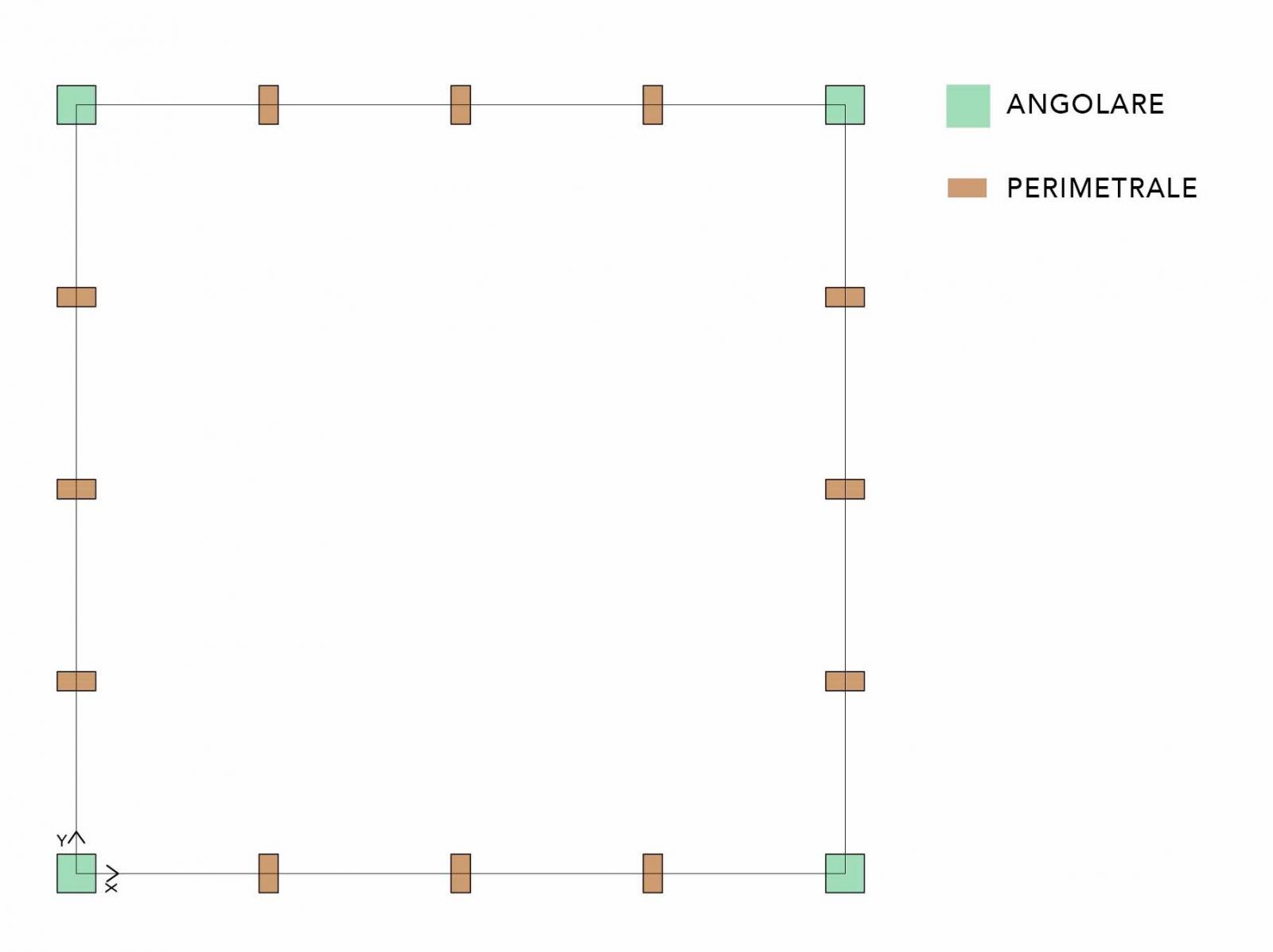
- Pilastri angolari 1,5 x 1,5 m
- Pilastri perimetrali 2 x 1,2 m
A questo punto abbiamo assicurato la stessa inerzia lungo le due direzioni x e y ruotando di 90 gradi gli assi locali dei pilastri appartenenti a due dei quattro lati della piastra.
Per completare la modellazione della geometria del modello abbiamo assegnato i vincoli esterni a terra di tipo incastro alla base di ogni pilastro. Assign>Joints>Restaints>Incastro.

Il passo successivo è stato quello di modellare la piastra con lo strumento "Poly area" e assegnarle una sezione "Shell" e selezionando la voce “Shell Thick”, che tiene conto anche dell’azione del taglio, assegniamo uno spessore di 1,50 m. Successivamente la piastra viene discretizzata in porzioni di 0,50 m x 0,50 metri, operazione che permette al programma di calcolo di eseguire un'analisi più accurata. Edit > Areas>Divide Areas> 0,50 x 0,50 m
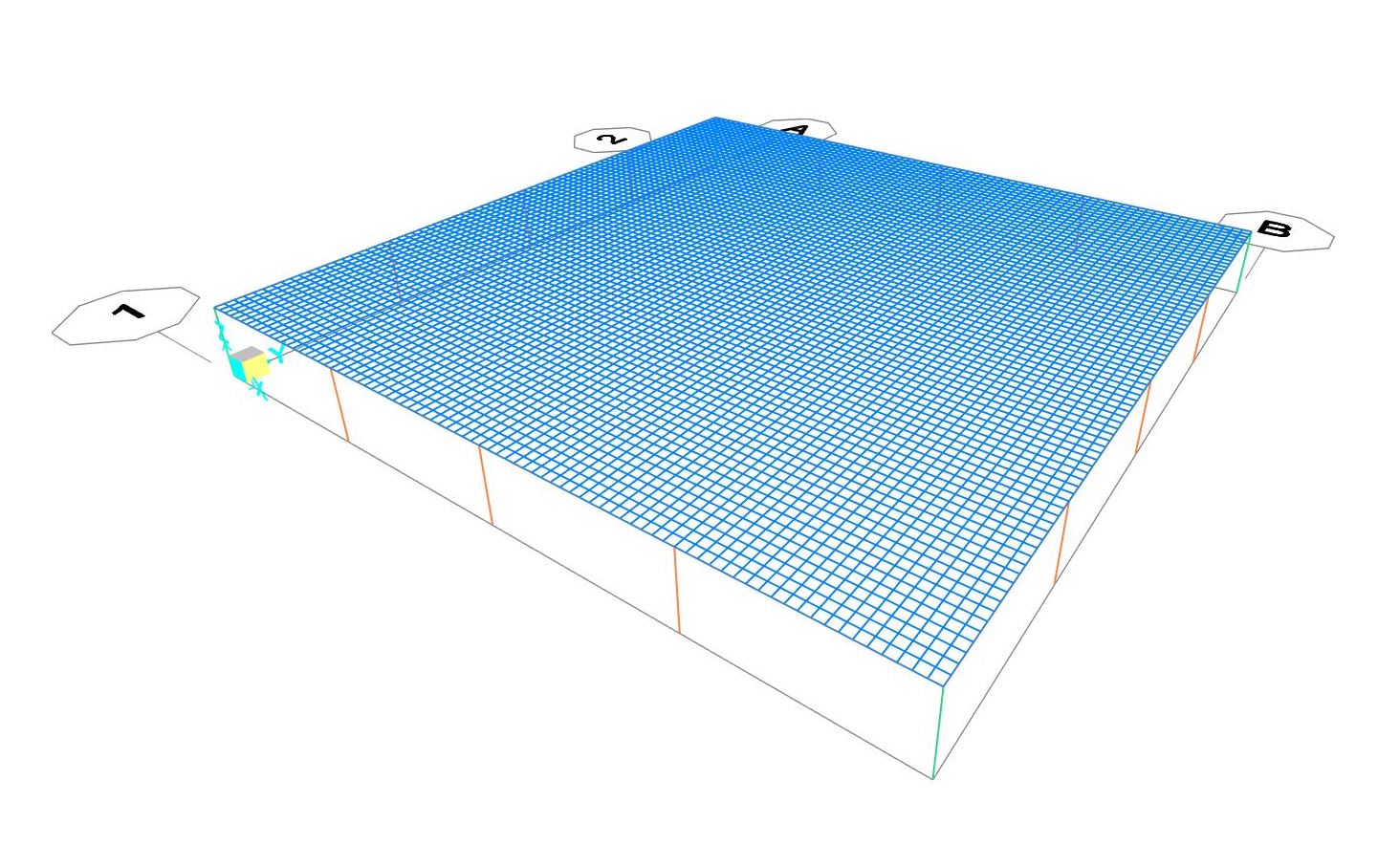
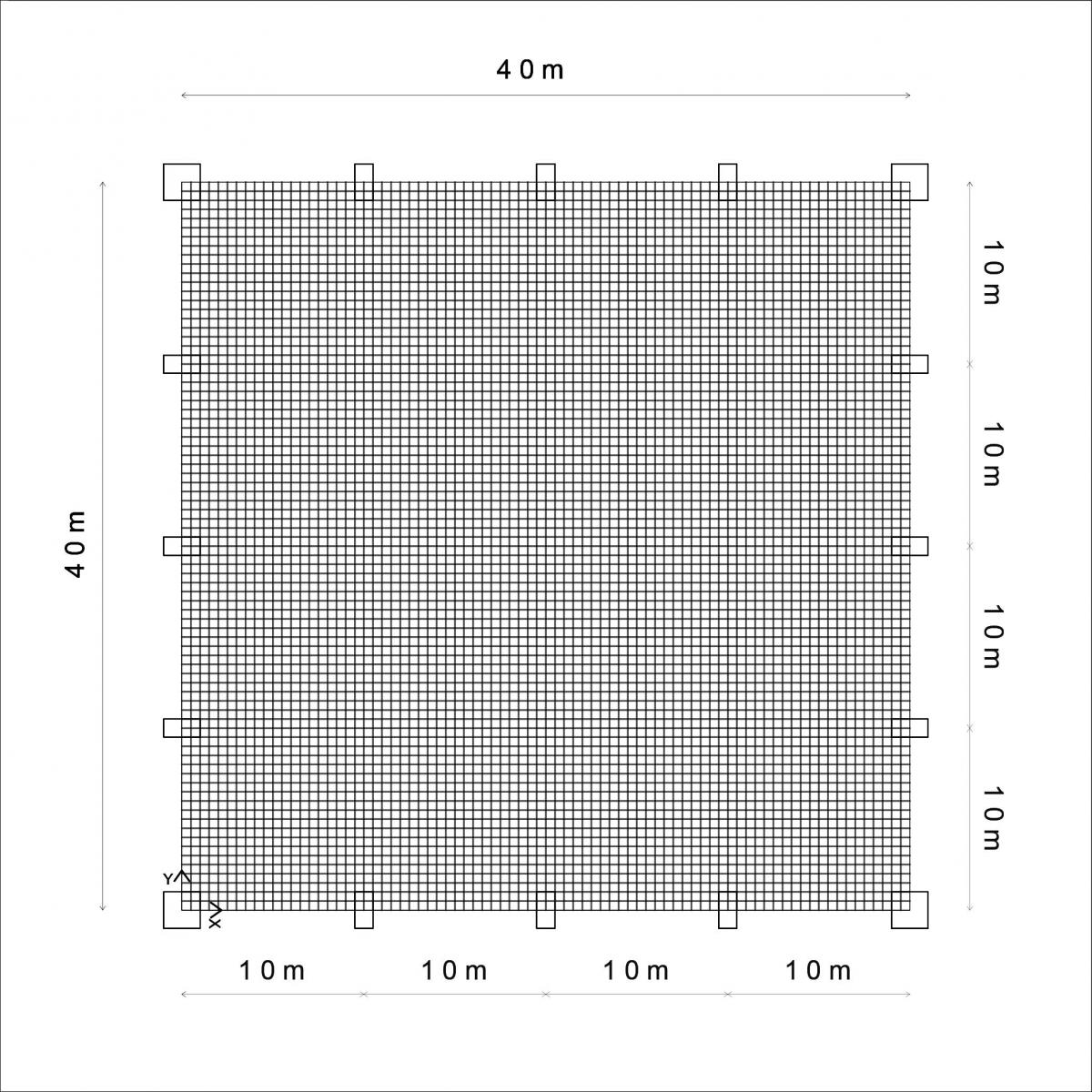

Dal momento che il modello che stiamo utilizzando è il modello di piastra,
Per poter simulare il comportamento di un graticcio di travi inflesse, utilizzando il modello di piastra come modello di riferimento, bisogna tener conto delle deformazioni secondarie presenti in un continuo dovute all'effetto Poisson che in questo caso saranno trascurabili.
Questo avviene perchè il graticcio composto da travi è assimilabile al modello di piastra dal punto di vista del comportamento meccanico mentre la geometria del graticcio non è assimilabile a quella di un continuo. Per poter trascurare questo comportamento, è stato definito un materiale fittizio a partire dal calcestruzzo ad alte prestazioni C50/60 ponendo il coefficiente di Poisson pari a zero.
A questo punto abbiamo definito il carico F_SLU e F_SLE considerando un fattore moltiplicatore di peso proprio pari a 1. Questo passaggio è necessario affinché nel calcolo del modello venga considerato anche il peso proprio della struttura che non può essere trascurato nel caso del calcestruzzo.
Una volta definiti i valori della forza concentrata equivalente, questi verranno distribuiti nei nodi a seconda dell'area di influenza di carico che inciderà in ogni nodo.

Da SAP troviamo che il numero totale dei nodi è 6561. Di questi, in base alle aree di influenza, sappiamo che quelli centrali prenderanno una forza concentrata pari al 100%, i nodi che si trovano sul perimetro prenderanno una forza concentrata parti al 1/2, quelli angolari prenderanno invece una forza concentrata pari al 1/4 del totale. Per trovare la forza totale che agisce su di un singolo nodo facciamo la somma di tutti i nodi centrali (che prendono il 100%) ai quali aggiungiamo la metà dei nodi perimetrali (che prendono il 1/2 della forza totale e perciò possiamo immaginarli come la metà dei nodi che prendono il 100% della forza) ai quali aggiungiamo infine uno solo dei quattro nodi angolari (che prende il 1/4 della forza totale quindi possiamo immaginare di considerare un solo nodo che prende il 100% della forza)
6241 (nodi centrali) + 316 (nodi perimetrali) + 4 (nodi angolari) = 6561 nodi

Per arrivare a definire lo stato limite d’esercizio e lo stato limite ultimo dividiamo il valore delle forze precedentemente calcolate per il numero di nodi e troviamo il valore della forza applicata ad un singolo nodo.
SLE
FTOT = 35064 KN / 6561 = 5,344 KN
- Nodi centrali F = 5,344 KN
- Nodi perimetrali F = 2,672 KN
- Nodi angolari F = 1,336 KN
SLU
FTOT = 66585,6 KN / 6561 = 10,148 KN
- Nodi centrali F = 10,148 KN
- Nodi perimetrali F = 5,074 KN
- Nodi angolari F = 2,537 KN
Applichiamo ai nodi centrali, perimetrali e angolari i valori precedentemente calcolati di F_SLU e F_SLE.
Ora possiamo avviare l'analisi del modello di piastra equivalente, prima con la combinazione di carico allo stato limite di esercizio e successivamente con la combinazione di carico allo stato limite ultimo.
VERIFICHE
Verifica agli abbassamenti
L'analisi con il carico allo SLE ci serve per la verifica degli abbassamenti
U3 = - 0,0391 m

Lo spostamento verticale deve essere inferiore a 1/200 della luce.
Essendo la nostra luce di 40 metri, l'abbassamento risulta verificato:
40 m / 200 = 0,20 m > 0,0391 m
Verifiche di resistenza
L'analisi con il carico allo SLU serve per svolgere la verifica di resistenza degli elementi inflessi e pressoinflessi. Dai diagrammi del momento flettente intorno agli assi locali 1 e 2 (rispettivamente i momenti M11, M22), notiamo che otteniamo gli stessi valori, questo perchè il sistema è perfettamente simmetrico, sia nella geometria che nei carichi applicati. Verifichiamo il valore massimo del momento, in corrispondenza di un pilastro, che equivale a 31942,7598 KNm.
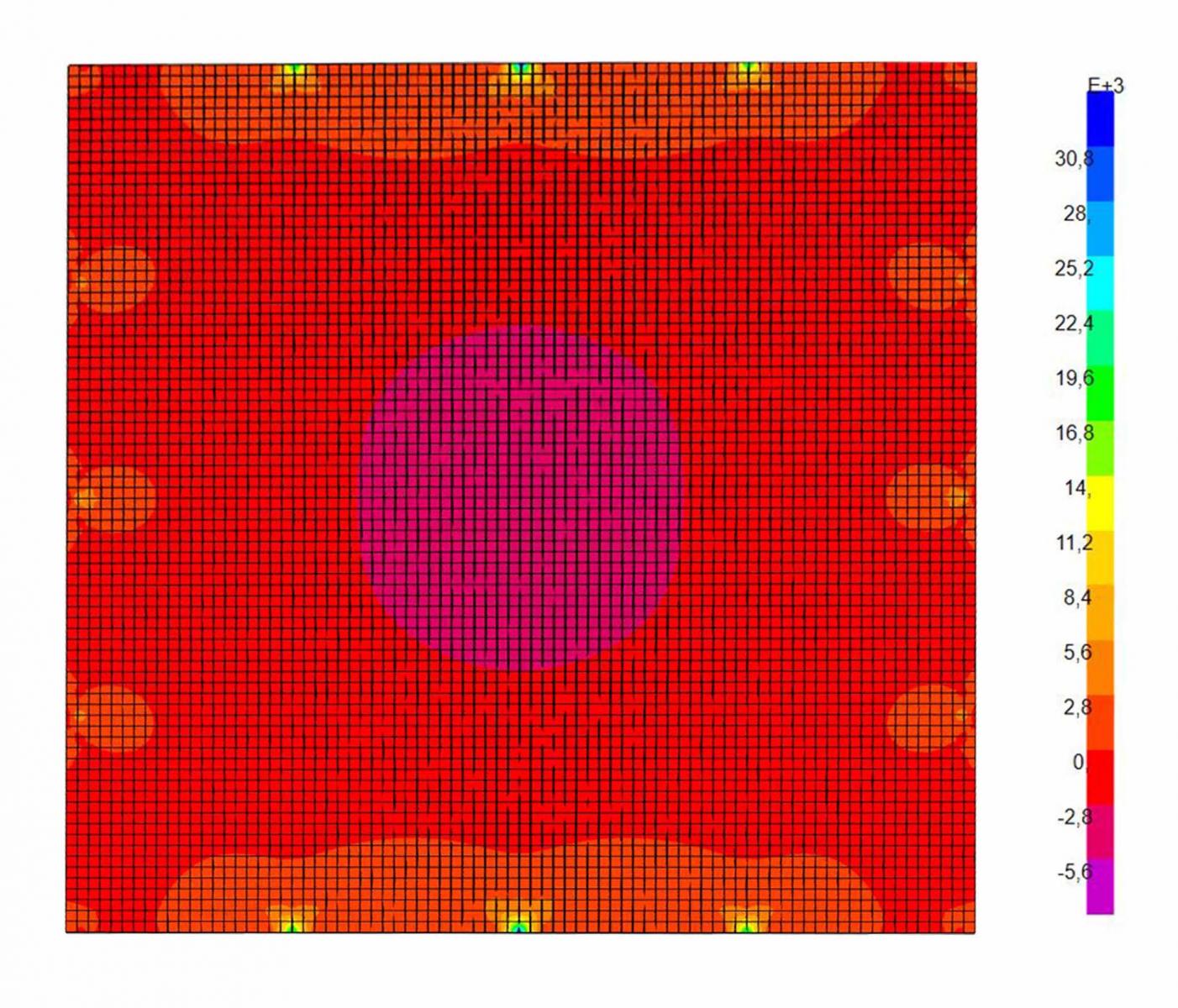
A questo punto, per verificare il dimensionamento della piastra abbiamo utilizzato la tabella Excel di verifica a flessione delle travi, ponendo come base uno spessore di 1,50 metri.
Verifica dimensionamento della piastra
![]()
Abbiamo ottenuto un valore di h utile maggiore rispetto a quella di progetto.
A questo punto siamo passati al dimensionamento del graticcio poichè abbiamo sfruttato il modello di piastra per creare un’equivalenza in rigidezza in base al momento di inerzia della sezione. L'equivalenza in rigidezza non implica però una equivalenza del peso della piastra rispetto a quello del graticcio, questo perchè il momento di inerzia è proporzionale alla terza potenza dell'altezza della sezione mentre il peso è proporzionale alla prima potenza dell'altezza della sezione. Questo è dovuto al fatto che il graticcio di travi inflesse, rispetto al modello di piastra, ha un peso notevolmente inferiore dato che non è un continuo pieno ma è formato da travi che si alternano a vuoti.
DIMENSIONAMENTO
Dimensionamento graticcio
Per dimensionare le travi del graticcio abbiamo calcolato il momento di inerzia di una porzione di piastra di dimensioni 1,00 m x 1,00 m
Ix = (bh3 / 12)
Ix = 1,00 m x (1,50 m)3 / 12 = 0,28125 m4
Da questo risultato sappiamo che in una porzione di graticcio di un metro quadrato non posso dare un valore di inerzia inferiore a quello ottenuto. A questo punto abbiamo scelto un interasse per le travi del graticcio pari ad i = 2,50 m.
In una porzione di interasse di 2,50 m avremo quindi una inerzia di:
Ix = (bh3 / 12)
Dove la base è 2,50 m
Ix = 2,50 m x (1,50 m)3 / 12 = 0,703125 m4
Ipotizziamo un valore della base delle travi del graticcio pari a 0,60 m e calcoliamo l'altezza della sezione sapendo che il momento di inerzia deve essere circa 0,70 m4
h = (12 Ix / b) 1/3
h = (12 x 0,703125 m4/ 0,60 m) 1/3 = 2,41 m --> 2,45 m
La sezione della trave del graticcio ottenuta è 0,80 m x 2,20 m
MODELLAZIONE GRATICCIO SU SAP2000
Nel modello precedentemente sviluppato, elimino la piastra discretizzata per sostituirla con le travi del graticcio appena dimensionate. Per simulare un nodo rigido interno ad ogni incrocio tra le travi e tra travi e pilastri, applico la ‘separazione’ tra le travi modellate ad ogni intersezione, in modo che non siano continue. A questo punto assegniamo nuovamente i carichi precedentemente calcolati su ogni nodo del graticcio. Per fare questo, dividiamo il valore delle forze per il numero di nodi e troviamo il valore della forza applicata ad un singolo nodo.
225 (nodi centrali) + 60 (nodi perimetrali) + 4 (nodi angolari) = 289 nodi
SLE
FTOT = 35064 KN / 289 = 121,3287 KN
- Nodi centrali F = 121,3287 KN
- Nodi perimetrali F = 60,6643 KN
- Nodi angolari F = 30,3321 KN
SLU
FTOT = 66585,6 KN / 289 = 230,4 KN
- Nodi centrali F = 230,4 KN
- Nodi perimetrali F = 115,2 KN
- Nodi angolari F = 57,6 KN
Assegniamo a questo punto ai nodi centrali, perimetrali e angolari i valori precedentemente calcolati, distinguendo sempre secondo le due combinazioni di carico.
F_SLE
F_SLU
Ora possiamo avviare l'analisi del modello del graticcio, prima con la combinazione di carico allo stato limite di esercizio e successivamente con la combinazione di carico allo stato limite ultimo.
VERIFICHE
Verifica agli abbassamenti
L'analisi con il carico allo SLE ci serve per la verifica degli abbassamenti.
Verifica agli abbassamenti SLE
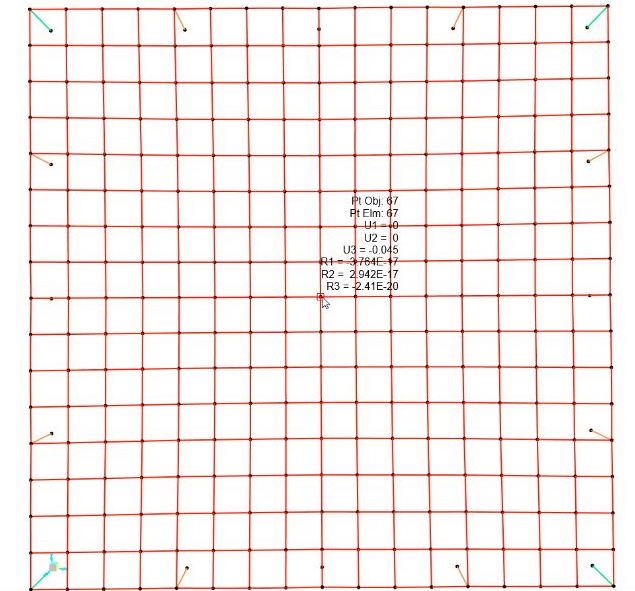
U3 = -0,045 m
Lo spostamento verticale deve essere inferiore a 1/200 della luce.
Essendo la nostra luce di 40 metri, l'abbassamento risulta verificato:
40 m / 200 = 0,20 m > 0,045 m
Se ci concentriamo su un pilastro perimetrale, notiamo che il valore del momento flettente è molto elevato in corrispondenza del nodo rigido tra trave e pilastro, questo comporterà una deformazione eccessiva del pilastro, che tenderà quindi ad instabilizzarsi.
VERIFICA DELLA TRAVE DI BORDO
![]()
VERIFICA DEI PILASTRI ANGOLARI
![]()
VERIFICA DEI PILASTRI PERIMETRALI
![]()
La nuova sezione verificata è pari a 2.00 x 1.80 m. A questo punto verrà definita una nuova sezione che verrà nuovamente riassegnata su SAP. Con l’avvio dell’analisi su SAP, e consultando i grafici delle sollecitazioni, si nota chiaramente che i valori migliorano.
VERIFICA FINALE
Verifica agli abbassamenti
L'analisi con il carico allo SLE ci serve per la verifica degli abbassamenti.
Verifica agli abbassamenti SLE
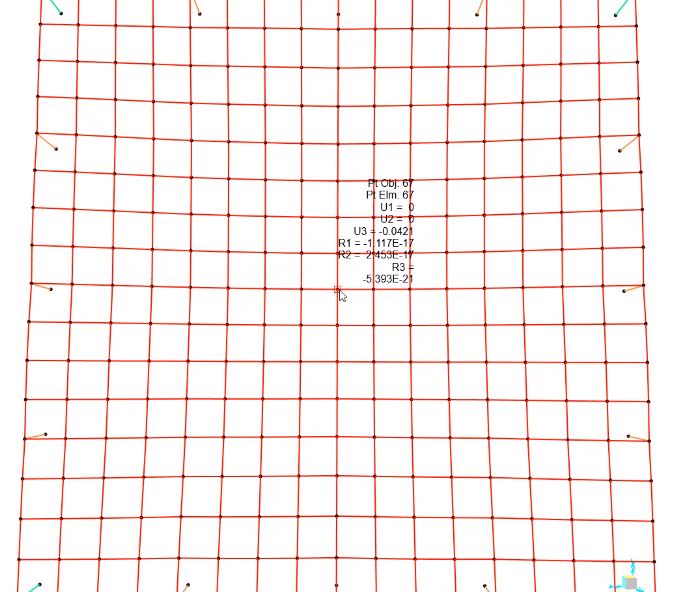
U3 = -0,0421 m
Lo spostamento verticale deve essere inferiore a 1/200 della luce.
Essendo la nostra luce di 40 metri, l'abbassamento risulta verificato:
40 m / 200 = 0,20 m > 0,0421 m
Verifiche di resistenza
L'analisi con il carico allo SLU serve per svolgere la verifica di resistenza degli elementi inflessi e pressoinflessi.
Diagramma dello sforzo normale
Diagramma del momento flettente
VERIFICA DELLA TRAVE DI BORDO
![]()
VERIFICA DEI PILASTRI PERIMETRALI
![]()

Commenti recenti