Giuli, Guglielmetti, Sigillò_ Esercitazione III
DIMENSIONAMENTO DI UN GRATICCIO IN C.A.
Pianta
Il graticcio è una struttura senza gerarchie, è un reticolo di travi in cui nel punto di intersezione tra le due travi, è presente un nodo rigido, che impedisce, quindi, la rotazione, in cui si concentrano i carichi o vengono appoggiati altri elementi strutturali. La geometria del graticcio deve essere il più possibile regolare, quindi, può avere una disposizione dei moduli quadrata, ma può avere anche una disposizione radiale, con travi curve.
Il graticcio simmetrico avrà quindi, nell’asse baricentro la tangente orizzontale.
Viene scelta una pianta rettangolare di dimensioni 40x20m, con modulo 2x2 m.
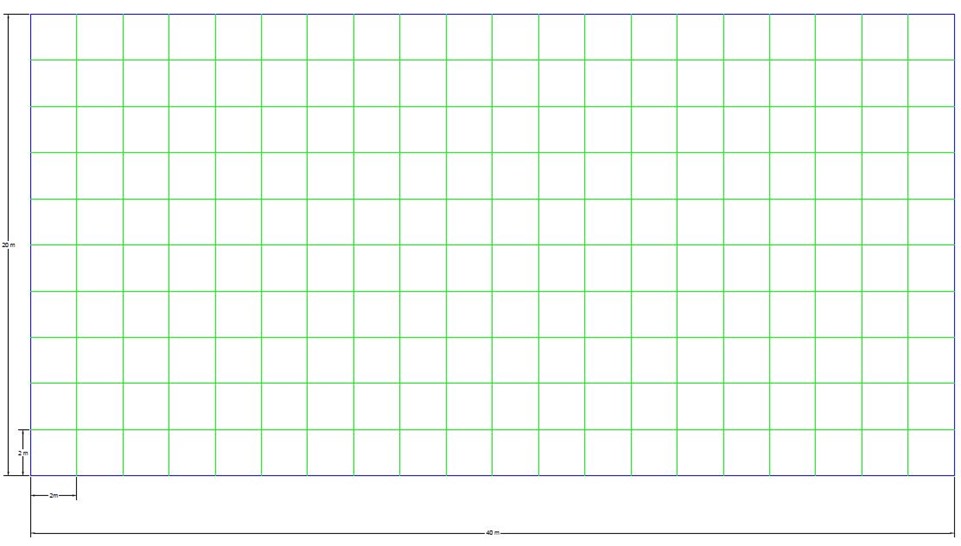
Viene definito come materiale il calcestruzzo, la classe C40/50 e viene definita la sezione delle travi, in cui consideriamo un primo dimensionamento di 1 x 0,4 m. Con le travi di bordo più grandi di 1 x 0,9 m.
Viene preso in considerazione il fatto che il graticcio sosterrà un peso di 4 piani.
Successivamente si deve calcolare FTOT che sarà una forza espressa in kN, quindi una forza concentrata, che corrisponda al peso di tutto l’edificio, quindi:
dove n= numero di solai.
Stratigrafia del solaio
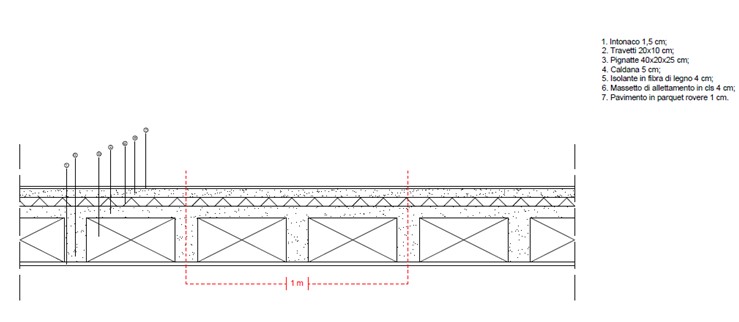
È stato ripreso il solaio dell’esercitazione precedente ed abbiamo:
Definiti i carichi, vengono considerate le combinazioni di carico fornite dalla normativa per le verifiche dello stato limite ultimo e dello stato limite d’esercizio utilizzando i coefficienti di sicurezza.
COMBINAZIONE ALLO STATO LIMITE D’ESERCIZIO
Questo valore servirà per le verifiche degli abbassamenti.
COMBINAZIONE ALLO STATO LIMITE ULTIMO
Questo valore servirà per le verifiche di resistenza degli elementi inflessi e presso inflessi (travi e pilastri).
Quindi
A questo si deve aggiungere il peso proprio del graticcio, che verrà aggiunto in SAP2000.
Definita la Forza, questa, deve essere attribuita ai nodi centrali, perimetrali e angolari.
Quindi, vengono calcolati quanti sono i nodi centrali, perimetrali e angolari.
Nc = 171
Np = 56
Na = 4
Nei nodi, la forza sarà moltiplicata per l’area di influenza. Quindi, se nel nodo centrale viene applicata una forza F, nei nodi perimetrali una forza F/2 mentre in quelli angolari una forza F/4.
Di conseguenza
Quindi, la forza da applicare al nodo sarà:
177,6 kN è la forza massima.
Quindi ai nodi centrali vengono assegnati i 177,6 kN; ai nodi perimetrali viene applicata la forza moltiplicata per 1/2, mentre ai nodi angolari viene applicata la forza moltiplicata per 1/4.
Quindi Fp = 88,8 kN e Fa = 44,4 kN.
Quindi, definita la forza su SAP2000 e posto il moltiplicatore di peso proprio pari a 1, viene assegnata a tutti i nodi.
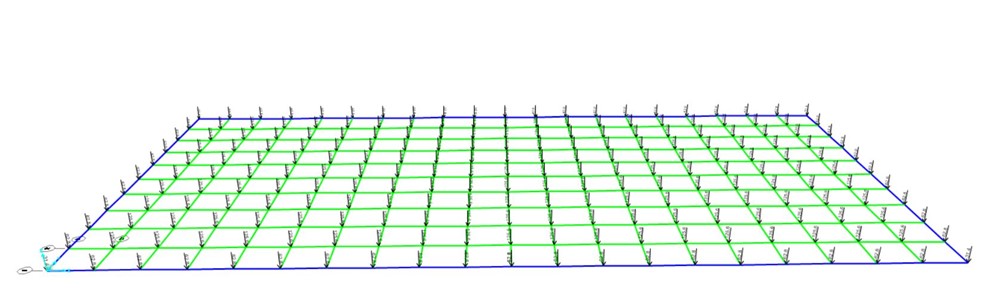
Stessa cosa viene fatta con la combinazione dello stato limite d’esercizio per la verifica degli abbassamenti.
Quindi:
Definita la Forza, questa, deve essere attribuita ai nodi centrali, perimetrali e angolari.
Quindi
La forza da applicare al nodo sarà:
102,56 kN è la forza massima.
Quindi ai nodi centrali vengono assegnati i 102,56 kN; ai nodi perimetrali viene applicata la forza moltiplicata per 1/2, mentre ai nodi angolari viene applicata la forza moltiplicata per 1/4.
Quindi Fp = 51,28 kN e Fa = 25,64 kN
Definita la forza su SAP2000 e posto il moltiplicatore di peso proprio pari a 1, viene assegnata a tutti i nodi.
ANALISI SAP2000
Viene fatta partire una prima analisi di SAP2000, in cui viene calcolata la forza F.
Deformata
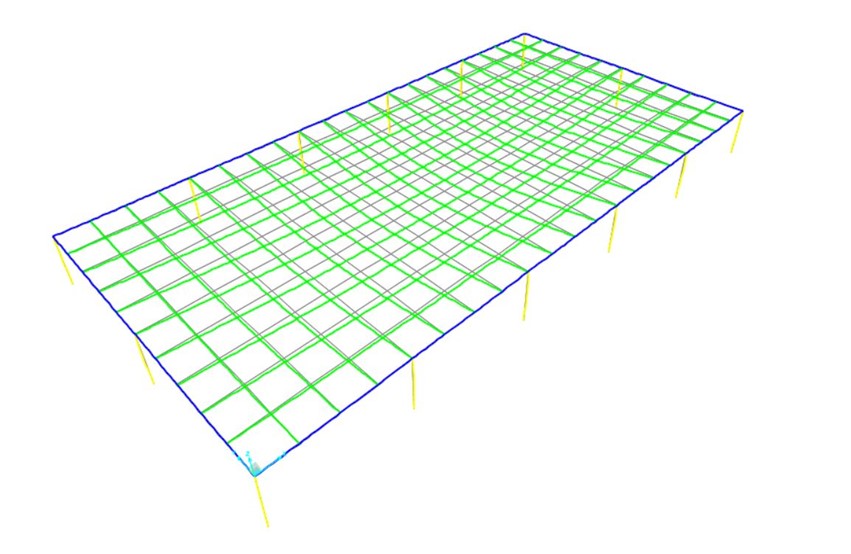
MOMENTO 3-3
Presenterà dei picchi proprio dove sono applicati i pilastri.
Sulla trave di bordo l’andamento è simile a quello di una trave continua, non uguale, perché non c’è continuità di momento. Questo perché siamo in una struttura tridimensionale in cui entra in gioco anche la trave ortogonale quella di bordo.
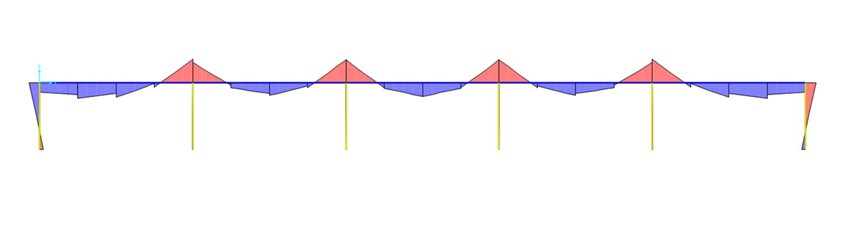Nelle travi centrali ortogonali alla trave di bordo, invece, il comportamento è quello di una trave inflessa. Notiamo che il momento non è proprio nullo agli estremi, perché lì c’è un nodo rigido e la trave centrale si innesta su un’altra trave che ha una sua deformazione e un suo comportamento. Comunque, le travi si inflettono tutte verso il centro.
MOMENTO 2-2
È presente anche il momento 2-2 perché sono presenti i pilastri. Sui pilasti il momento agisce in entrambe le direzioni.
Quindi, dobbuamo considerare entrambi i momenti.
VERIFICHE
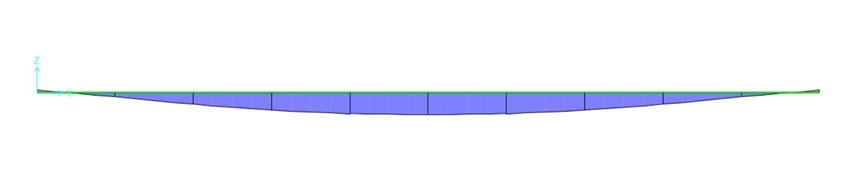
Come prima verifica si prosegue con l’ABBASSAMENTO MASSIMO, fatto con il carico SLE.
Lo spostamento verticale deve essere inferiore a 1/200 della luce. La nostra è di 40 m.
Estrapolando le tabelle da SAP2000 riguardanti l’abbassamento dei punti, possiamo verificare che il punto che subisce maggiore spostamento verticale è il 154.
Il punto 154 subisce un abbassamento di 0,025 m.
Quindi
L’abbassamento massimo risulta verificato.
Ora passiamo alla VERIFICA DELLE TRAVI, fatta con il carico SLU. Estrapoliamo le tabelle soltanto delle travi e non dei pilastri.
Le ordiniamo e prendiamo il momento massimo da verificare.
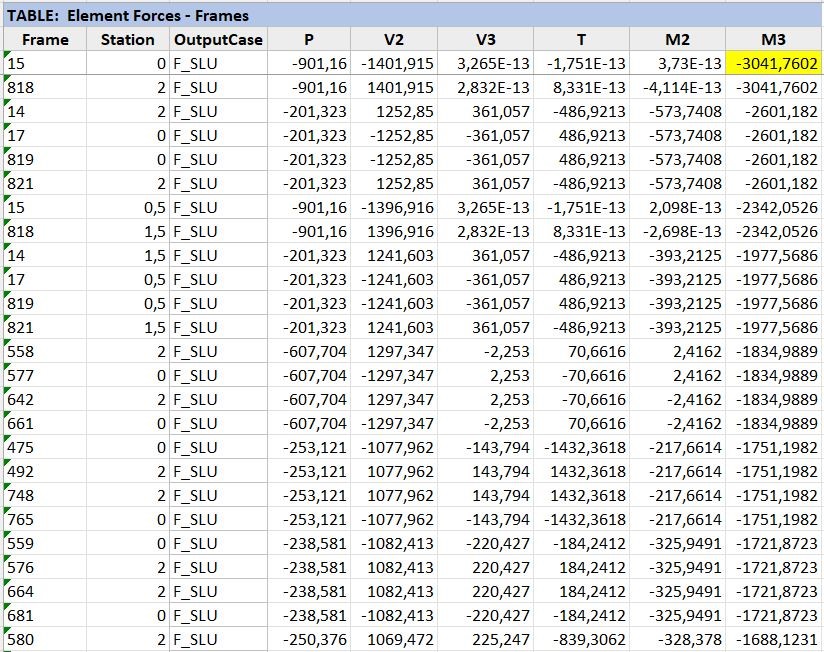
Notiamo che il momento maggiore lo troviamo nelle travi 15 e 818 (cioè la sua speculare).
Trovando queste travi sul modello SAP2000, vediamo che sono le travi che si trovano sul lato corto ortogonali alla trave di bordo.
Il valore del momento massimo delle travi lo inseriamo nella tabella delle travi, e notiamo che inserendo tutti i dati, i valori non risultano verificati.
Quindi, proviamo a cambiare la base e l’altezza delle travi e notiamo come con una base di 60 cm con abbiamo bisogno di un’altezza di 115 cm.
Quindi, torniamo su SAP2000 e modifichiamo le basi e le altezze delle travi centrali e le altezze delle travi di bordo, perché le travi centrali e quelle di bordo devono almeno avere la stessa altezza.
TRAVE CENTRALE SOGGETTA A FLESSIONE: 60 x 115 cm;
TRAVE DI BORDO: 90 x 115 cm.
Estrapoliamo la tabella con un nuovo momento massimo:
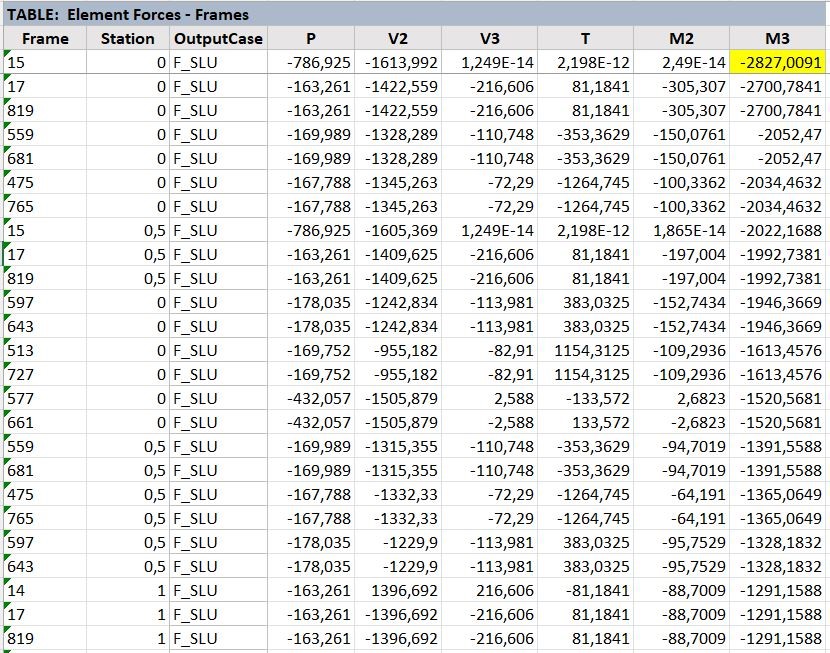
Verifichiamo questo nuovo momento massimo:
La trave risulta verificata
Quindi:
TRAVE CENTRALE SOGGETTA A FLESSIONE: 60 x 115 cm;
TRAVE DI BORDO: 90 x 115 cm.
DIMENSIONAMENTO E VERIFICA DEI PILASTRI
Passiamo ora al DIMENSIONAMENTO DEI PILASTRI.
Sappiamo che:
PESO UNITARIO TRAVE DI BORDO 25,875 Kn/m
PESO UNITARIO TRAVE 17,25 Kn/m
Da un primo dimensionamento risultano le seguenti sezioni:
PILASTRO D’ANGOLO N.830: 60 x 80 cm;
PILASTRO PERIMETRALE N.831: 80 x 100 cm;
PILASTRO PERIMETRALE N.842: 120 x 150 cm.
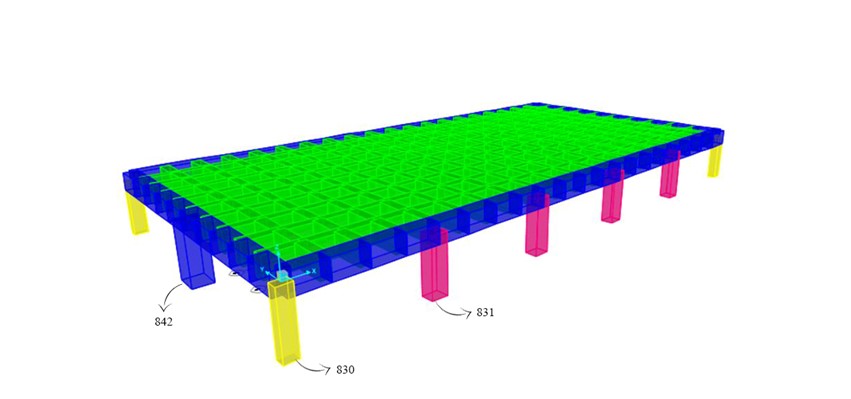
SFORZO NORMALE
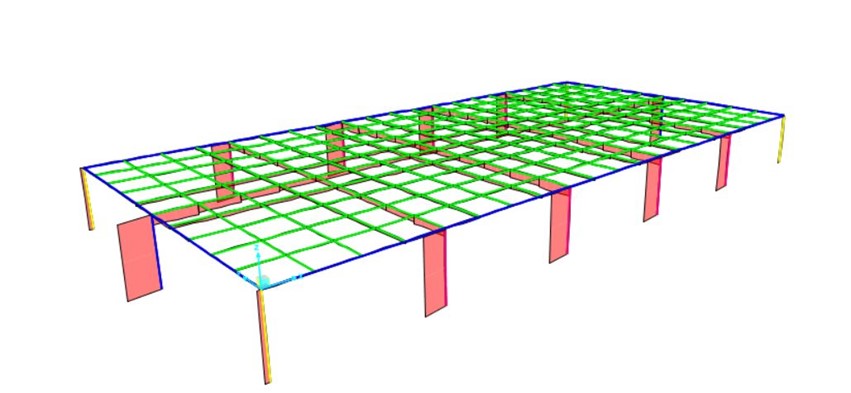
MOMENTO 2-2
MOMENTO 3-3
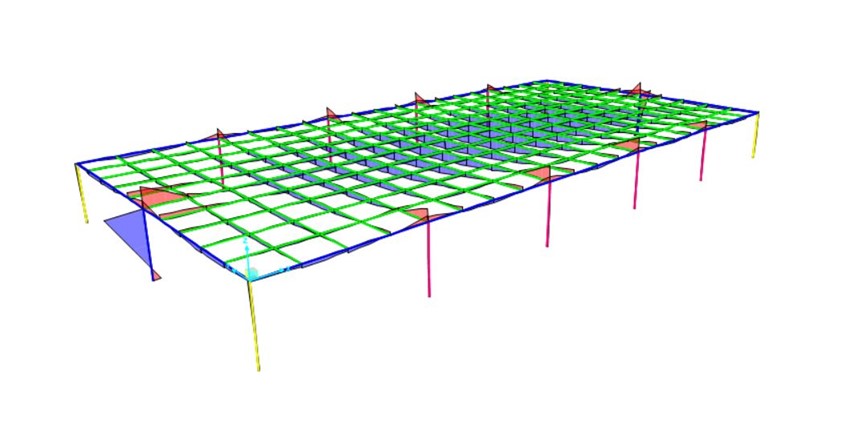
TABELLA SAP2000 PILASTRI.
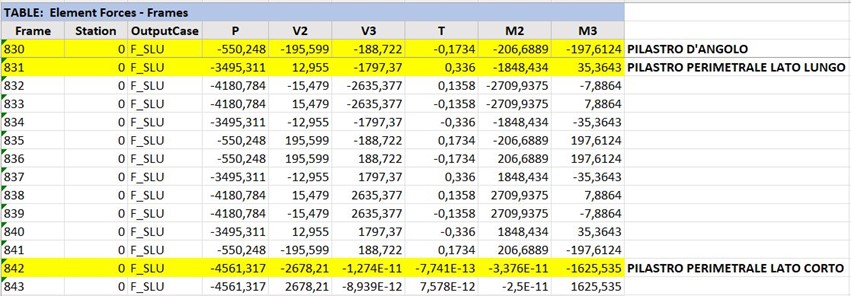
VERIFICA A PRESSOFLESSIONE
Verifica a piccola eccentricità
Da una prima verifica, i pilastri d’angolo e quello perimetrale sul lato lungo non risultano verificati a piccola eccentricità.
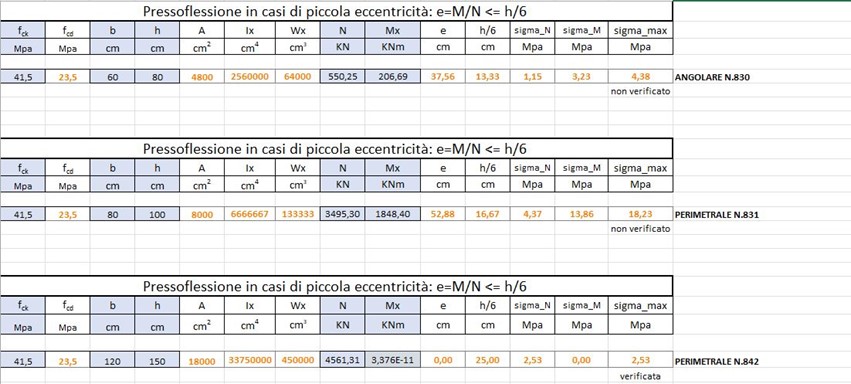
Quindi, aumentiamo le sezioni dei pilastri non verificati.
Risultano verificate le seguenti sezioni:
PILASTRO D’ANGOLO N.830: 150 x 180 cm;
PILASTRO PERIMETRALE N.831: 150 x 180 cm;
PILASTRO PERIMETRALE N.842: 120 x 150 cm.
TABELLA SAP2000 PILASTRI
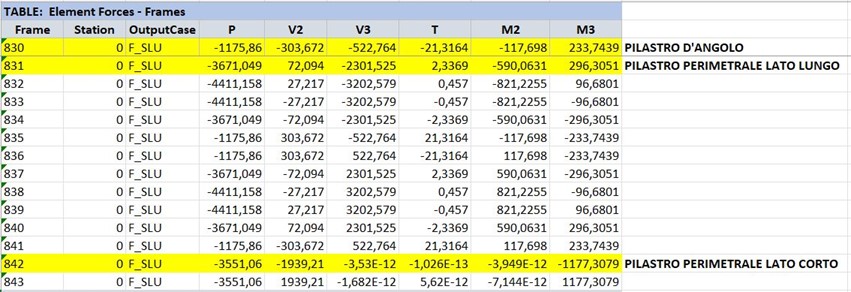
VERIFICA A PRESSOFLESSIONE
Verifica a piccola eccentricità
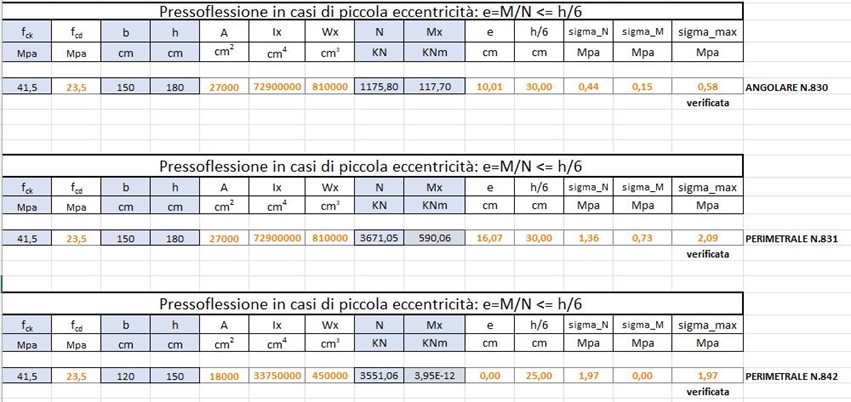
DEFORMATA
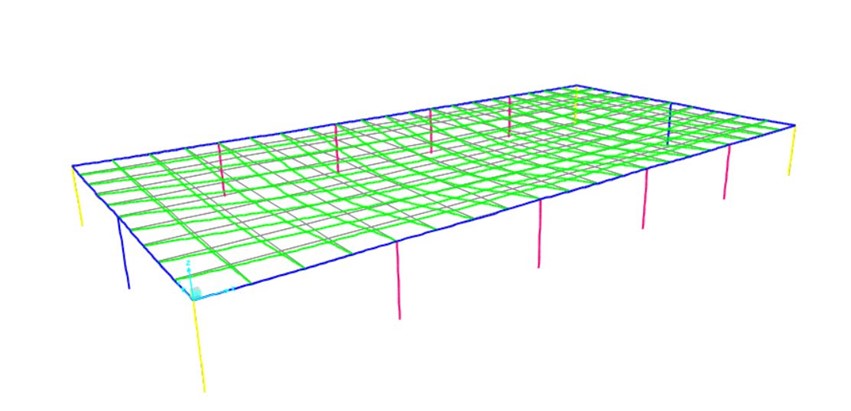
SFORZO NORMALE
MOMENTO 2-2
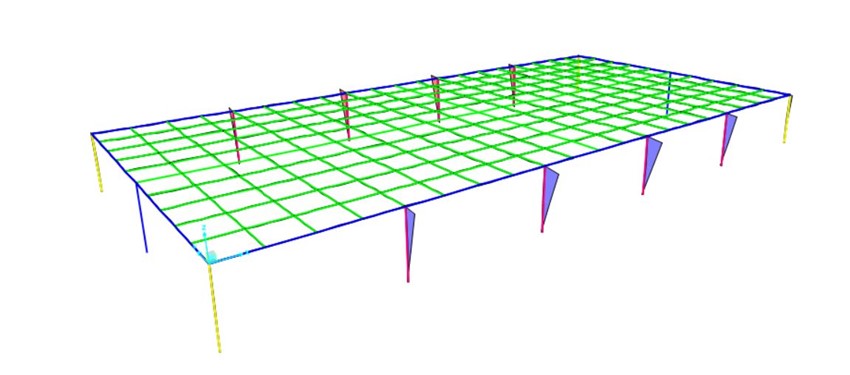
MOMENTO 3-3
TORSIONE DELLA TRAVE DI BORDO
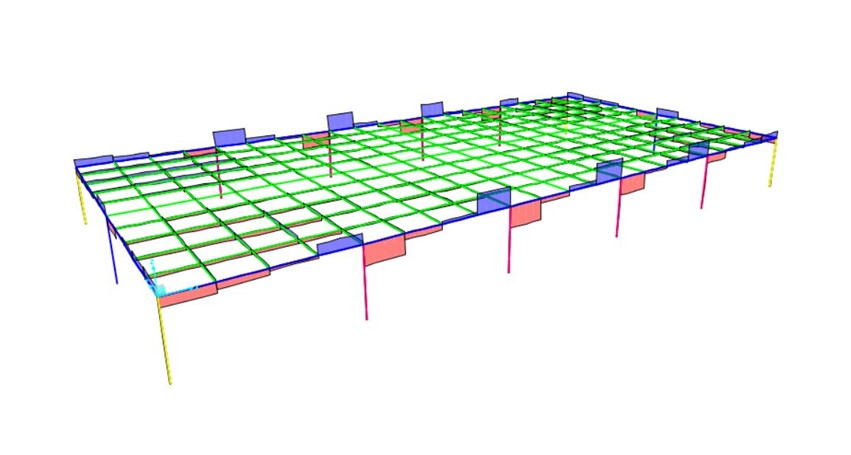
Da SAP2000 estrapoliamo le tabelle della torsione, notiamo che la trave con maggiore Momento torcente Mt, è la n.580, e la sua speculare la trave n.660 dove:
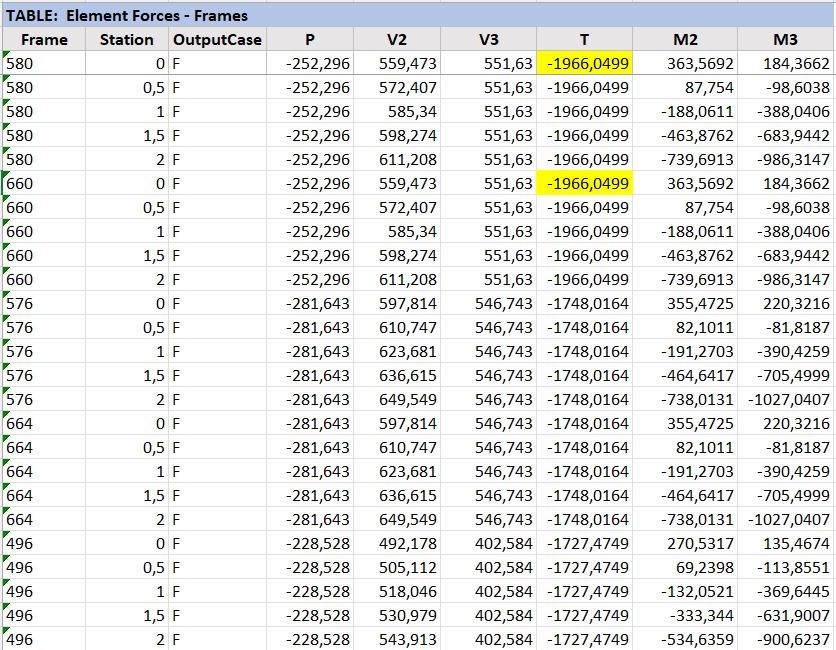
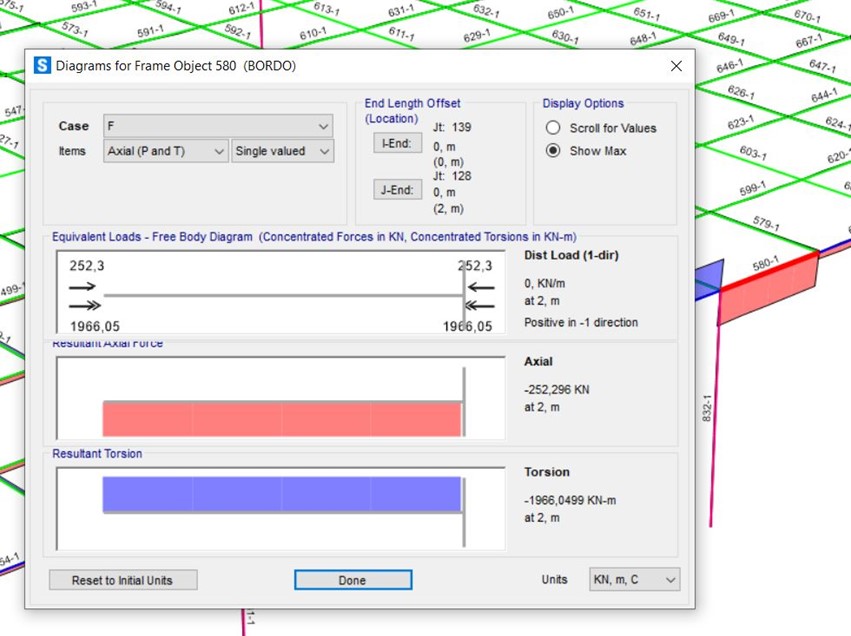
Ora è necessario determinare la tensione massima:
Dove Mt
è il momento torcente che sollecita la sezione;
a e b sono i lati della sezione dove a è il lato lungo;
α è un coefficiente che dipende dal rapporto a/b.
TRAVE DI BORDO: 90 x 115 cm
Quindi
a = 1.15 m
b = 0.9 m
per cui si trova che
Sapendo che è stato preso il calcestruzzo C40/50, con Rck = 50 e sapendo che
In questo caso, è necessario aumentare la sezione della trave di bordo, ma questo comporterebbe una maggiore deformazione del pilastro. Quindi, per aumentare la rigidezza torsionale della trave di bordo, possiamo utilizzare una sezione rettangolare cava, in questo modo è possibile avere una maggiore larghezza della trave di bordo senza gravare ulteriormente sul pilastro.
In conclusione, tutti i pilastri sono verificati a presso flessione, tutte le travi sono verificate a flessione, ma le travi di bordo, non essendo verificate a torsione, assumeranno una sezione rettangolare cava.
Commenti recenti