Calcolo struttura reticolare asimmetrica con il metodo dei nodi

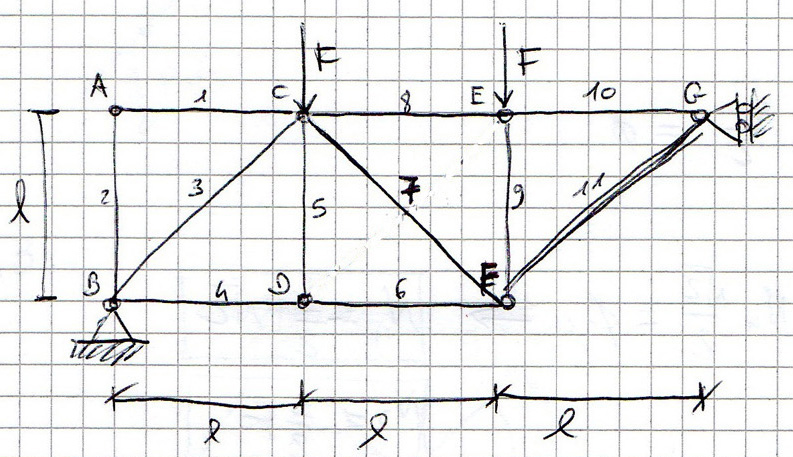
In questo esercizio ci troviamo di fronte ad una struttura reticolare asimmetrica.

Come fatto per l' esercizio precedente prima di tutto dobbiamo verificare che la struttura sia isostatica:

Passo 1

Per verificare l' isostaticità dobbiamo vedere se il numero dei vincoli (esterni e interni) e quello dei gradi di libertà è uguale:

V = l

Il numero di gradi di libertà è dato dal prodoto del numero delle aste per i gradi di libertà di ogni elemento:

l = 11 (aste) x3 (gradi di libertà) =33

Il numero di vincoli è dato dalla somma dei vincoli interni e esterni:

I vincoli esterni sono una cerniera, che blocca 2 gradi di libertà, e un carrello che blocca 1 gdl.

V_e = 3

Calcoliamo i vincoli interni con la formula: V_i = 2*(n -1) dove n è il numero di aste che arriva alla cerniera:

A-G = 2(2-1) = 2

B-D-E = 2(3-1) = 4

F = 2(4-1) = 6

C = 2(5-1) = 8

Avrò percio V_i = 30 che sommato al contributo di V_e da V = 33 = l     VERIFICATO!

Passo 2

Calcolo ora le reazioni vincolari con l' equilibrio alla traslazione e alla rotazione:

Sostituisco i vincoli con le loro reazioni e imposto le equazioni di equilibrio:

- Equilibrio alla traslazione orizzontale

U_B - U_G = 0 ----> U_B = U_G

- Equilibrio alla traslazione verticale

V_B - 2F = 0 ----> V_B = 2F = 20 kN

- Equilibrio alla rotazione in B

- F*l - F*2l + U_G*l = 0 ----> U_G = 30 kN = U_B

Disegno ora la struttura equilibrata:

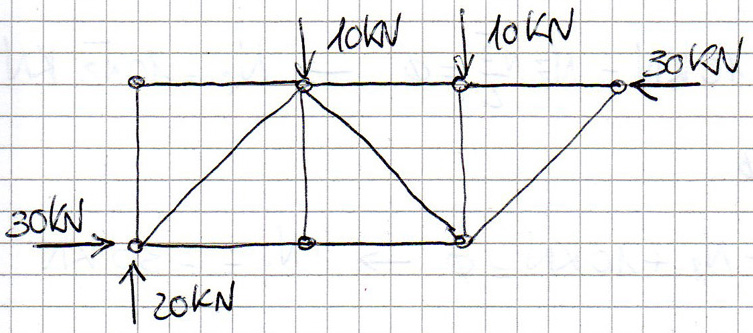
Passo 3

Calcolo ora le azioni di contatto con il metodo dei nodi. Isoliamo cioè ogni nodo e calcoliamo l' equilibrio:

Nodo A

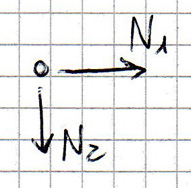
- Equilibrio alla traslazione orizzontale  N₁ = 0

- Equilibrio alla traslazione verticale  N₂ = 0

Nodo B

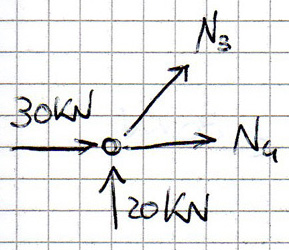
- Eq. trasl. orizzontale  30 kN + N₄ + N₃* √2/2 = 0

- Eq. trasl. verticale  20 kN + N₃* √2/2 = 0 ----> N₃ = -20√2 kN

                                                                          N₄ = - 10 kN

Nodo D

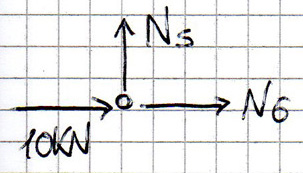
- Eq. trasl. orizzontale  10 kN + N₆ = 0 ----> N₆ = 10 kN

- Eq. trasl. verticale   N₅ = 0

Nodo C

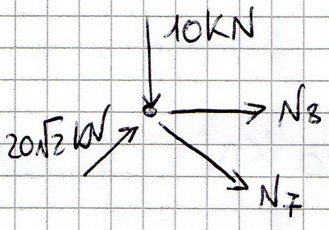
- Eq. trasl. orizzontale  20 kN + N₈ + 10 kN = 0 ----> N₈ = -30 kN

- Eq. trasl. verticale  20 kN - 10 kN - N₇*√2/2 = 0 ----> N₇ = 10√2 kN

Nodo F

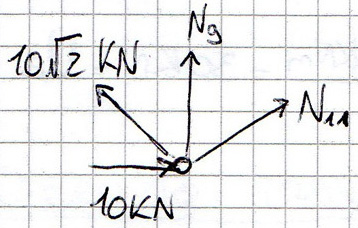
- Eq. trasl. orizzontale   10 kN + N₁₁*√2/2 - 10 kN = 0 ----> N₁₁ = 0

- Eq. trasl. verticale   N₉ + 10 kN = 0 ----> N₉ = -10 kN

Nodo G

- Eq. trasl. orizzontale   N₁₀ = - 30 kN

Posso disegnare ora la struttura con gli sforzi assiali di ogni asta:

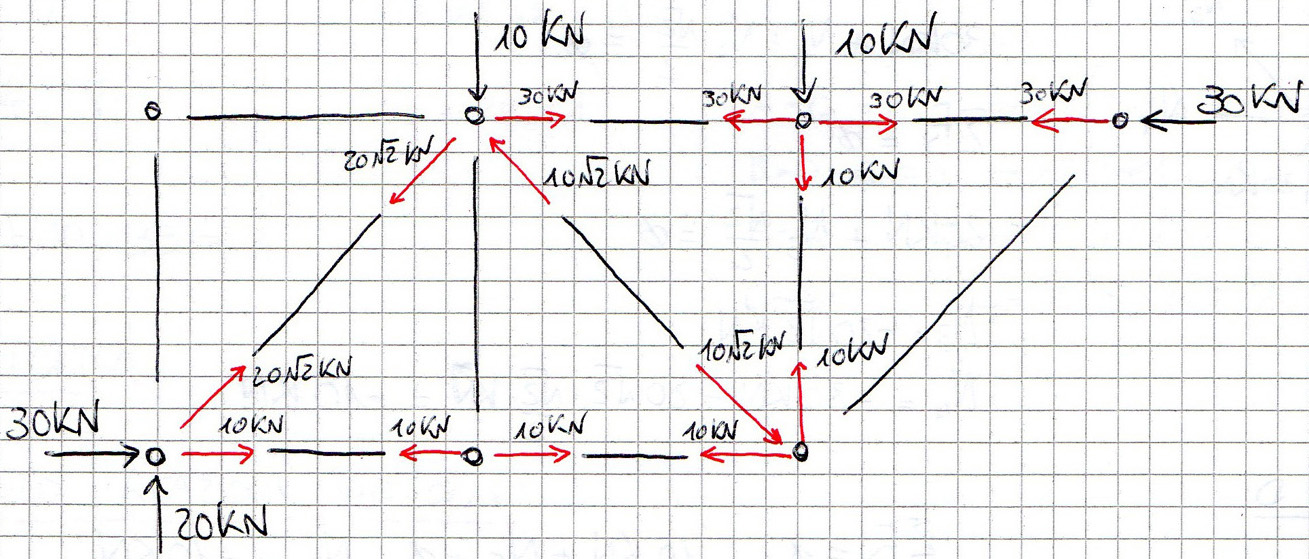
Possiamo notare come alcune aste nella struttura sono scariche.

Passo 4

A questo punto verifico se i calcoli sono giusti tramite SAP2000:

Reazioni vincolari.

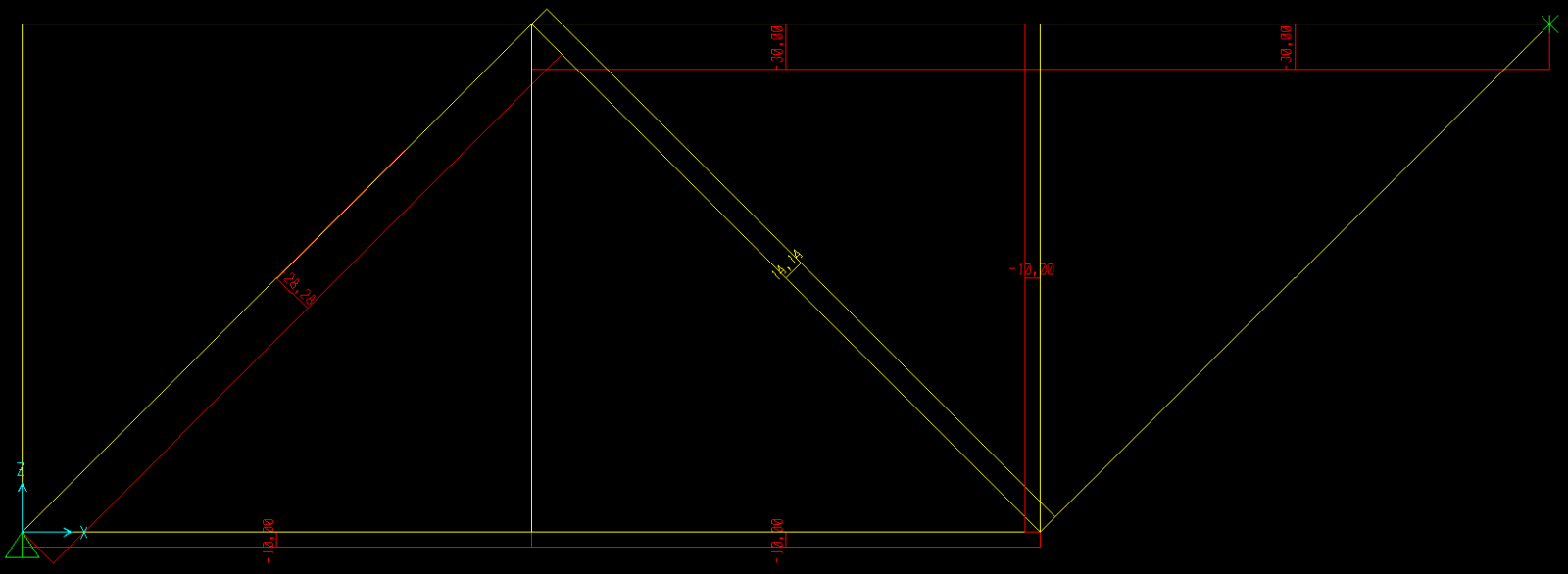
Diagramma sforzo assiale.