ESERCITAZIONI

Prima Esercitazione

Dimensionamento trave( svolto con Chiara Di Battista)

L’impalcato che abbiamo scelto  è frutto di un primo ragionamento sulla struttura del nostro albergo (Prof. Cordeschi). Il sistema distributivo delle stanze prevede un corridoio di 2,40 m di larghezza e le stanze di 4 metri di interasse in larghezza e 6 m in profondità. Abbiamo scelto di dimensionare la trave 2-7 che copre una luce di 6,00 m e un interasse di 4,00 m. La sua area d’influenza è quindi pari a 6,00 x 4,00 = 24,00 mq.

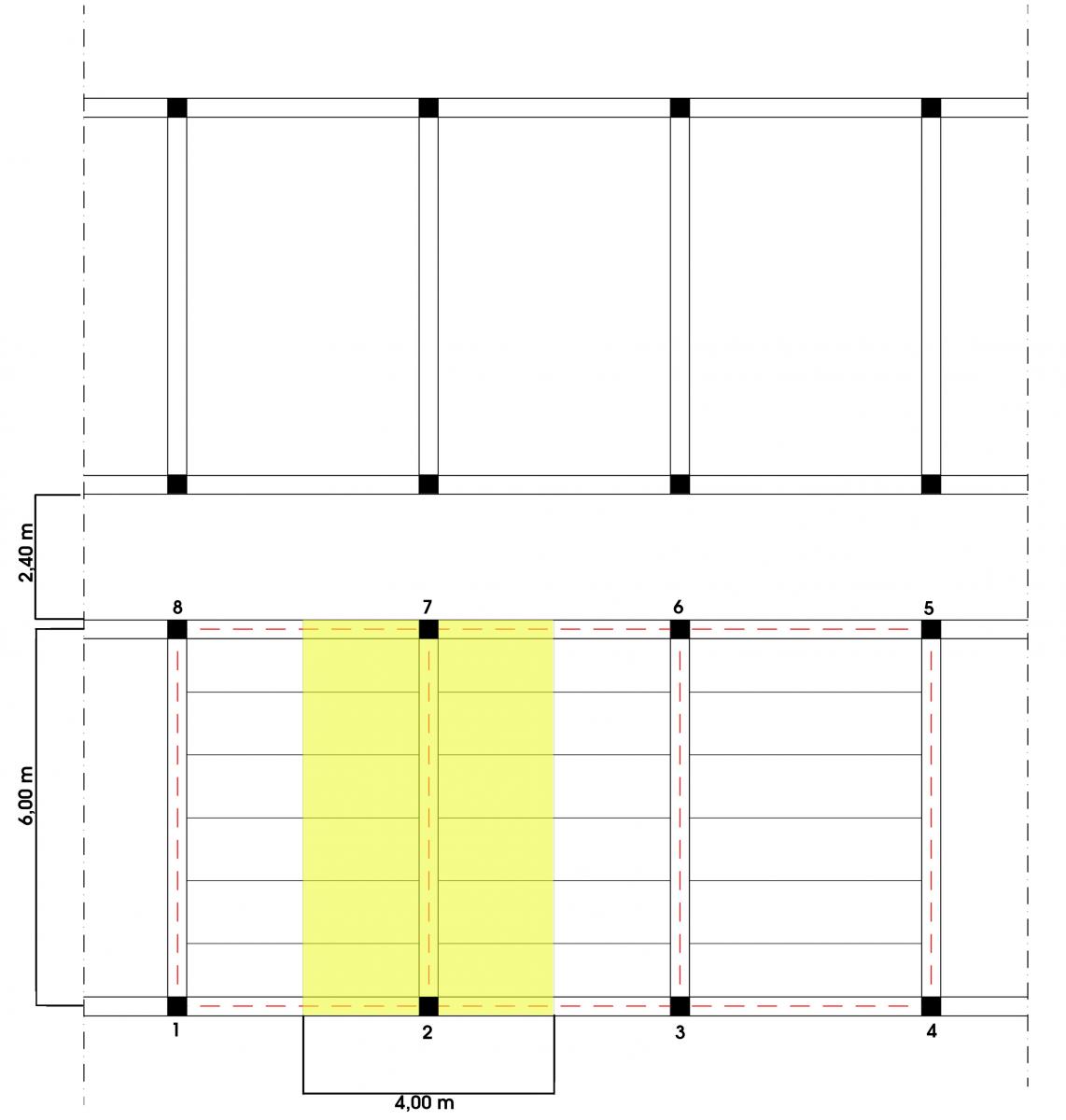
Per il dimensionamento corretto della trave è necessario calcolare Qs, Qp e Qa dove Qs (carico strutturale) indica il carico proprio della struttura; Qp (carico permanente) indica tutti quegli elementi non strutturali ma che permangono durante la vita della struttura e Qa indica il valore del carico accidentale legato all’uso che si farà di quell’ambiente.

Trattandosi di stanze di un albergo abbiamo deciso di utilizzare come valore di carico accidentale quello relativo  ai locali ad uso civile: 2,00 KN/Mq.

Ciascuno carico a mq è frutto della somma dei pesi (calcolati a mq) degli elementi che lo costituiscono:

P= V x γ / A  dove V è il volume dell’elemento, γ è il peso specifico del materiale e A è l’area in questo caso relativa ad 1 mq di struttura.

Struttura in legno

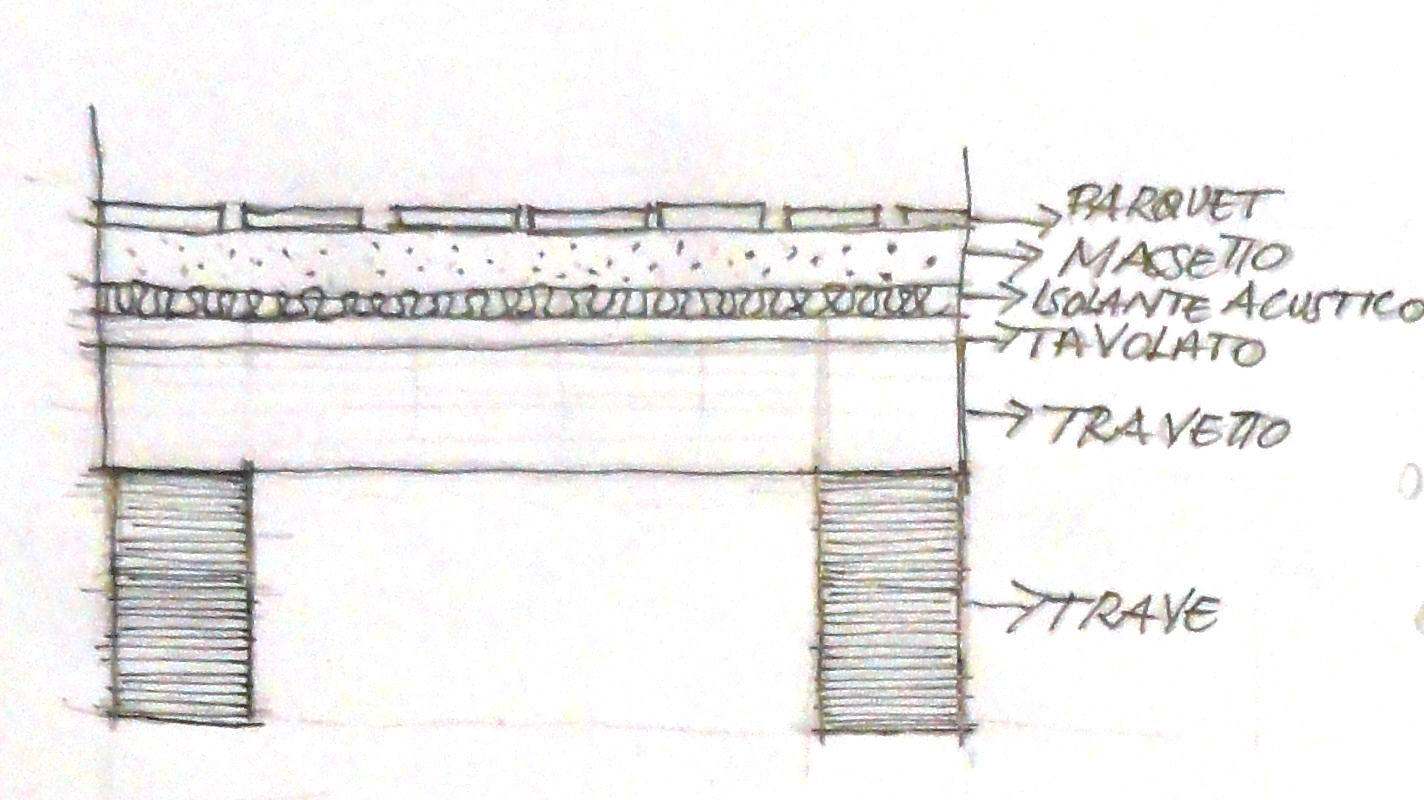
a)Dimensionamento del travetto (interasse 1m, luce 4m):

Partiamo con il dimensionamento del travetto prendendo come carico strutturale iniziale quello del    tavolato.

Qs:

-Tavolato:  

spessore :  0,045 m

peso specifico: 700 Kg/mc

Volume: 0,045 x 1 x 1 = 0,045 mc

Peso: 0,045 x 700 = 31,5 Kg    0,315 Kn

Peso a mq:  0,315 Kn/1 mq

Qp:

-Isolante acustico  (Acustic system 7):(vedi a:http://www.termoisolanti.com/prodotti/isolanti-acustici/sistemi-fonoisol...)

Spessore: 0,007 m

Peso a mq:  3 Kg/mq   0,03 kn/mq   (fornito dalla casa produttrice)

-Massetto in cls:

Spessore:  0,08 m

Peso specifico: 2000Kg/mc

Volume: 0,08 x 1 x 1 =0,08 mc

Peso: 0,08 x 2000 = 160 Kg   1,6 KN

Peso a mq: 1,6 kn/mq

-Parquet in ciliegio:

Spessore: 0,02 m

Peso specifico: 850 Kg/mc

Volume: 0,02 x 1 x 1= 0,02 mc

Peso: 0,02 x 850= 17 Kg    0,17 KN

Peso a mq: 0,17 KN/mq

-Incidenza impianti:

Peso a mq: 0,5 KN/mq

-Incidenza tramezzi:

Peso a mq: 1 Kn/mq

Qp tot: 0,03+1,6+0,17+0,5+1= 3,3 KN/mq

Qa:

-Civile abitazione:    2 KN/mq

Inseriamo i dati nella tabella excel.

La formula presente nella tabella Excel relativa al momento è ql^2/8, che in  questo caso è valida poichè si tratta di una trave doppiamente appoggiata.

Ad esempio se si fosse trattata di una trave  a sbalzo, l'espressione sarebbe stata ql^2/2.

Dalla tabella possiamo leggere che con i carichi inseriti e assumendo una base per il travetto di 0,12m l’altezza deve essere non inferiore a 0,2201 m.

Abbiamo cosi scelto un travetto della casa produttrice Canducci  GL24H  120x240 mm.  (http://www.mmk-canducci.it/)

Dove la classe di resistenza GL24H indica una resistenza  a flessione di 24N/mmq e dove Kmod è il coefficente moltiplicativo in funzione della durata del carico.

Normalmente K mod è compreso tra 0,5 e 1. In questo caso prendiamo un Kmod ipotetico di 0,7 e lo inseriamo nella tabella excel.

Il passo successivo è stato quello di calcolare il peso a mq del travetto scelto e di inserirlo all’interno dei Qs nella nostra tabella excel.

Peso specifico: 550 Kg/mc

Volume: 0,12 x 0,24 x 1= 0,029 mc

Peso: 0,029 x 550= 15,95 Kg      0,1595 KN   

Peso a mq:  P x 1/ interasse     0,1595 x (1/1)= 0,1595 KN/mq

Qs tot:   Tavolato più travetti    0,315 + 0,159 =0,474 KNmq

Inserendo il peso del travetto dalla tabella ci compare che assumendo di nuovo una base di 0,12 m  l’altezza risulta essere di 0,2232 m. Il travetto da noi scelto era di 0,12 x 0,24 m. La sezione è quindi verificata.

 

b) Dimensionamento trave (luce 6 m, interasse 4m)

A questo punto possiamo inserire nella tabella la luce e l’interasse relativi alla trave (mantenendo gli stessi carichi).

Ne risulterà, assumendo come base 0,24 m, un’altezza di 0,4101 m.

Abbiamo proceduto con la scelta di una trave che soddisfacesse le misure richieste.

La trave scelta è una GL32H 240 x 440 mm.

Calcolo il peso della trave:

Volume: 0,24 x 0,44 x 1= 0,1056 mc

Peso specifico: 550 Kg

Peso: 0,1056 x 550= 50,08 Kg     0,5808 KN

Peso a mq:  px1/i=0,5808 x 1/4= 0,1452 KN/mq   dove:i=4 m = interasse trave

A questo punto possiamo sommare il peso della trave agli altri valori in Qs:

Qstot: 0,474 + 0,1452 = 0,619 KN/mq

Abbiamo inserito il nuovo valore del carico strutturale all’interno della tabella excel e ciò che ne risulta è una trave di 24 x 41,52 cm,    trave con dimensioni minori rispetto a quella scelta da noi.

La scelta della trave è quindi verificata.

Struttura in acciaio

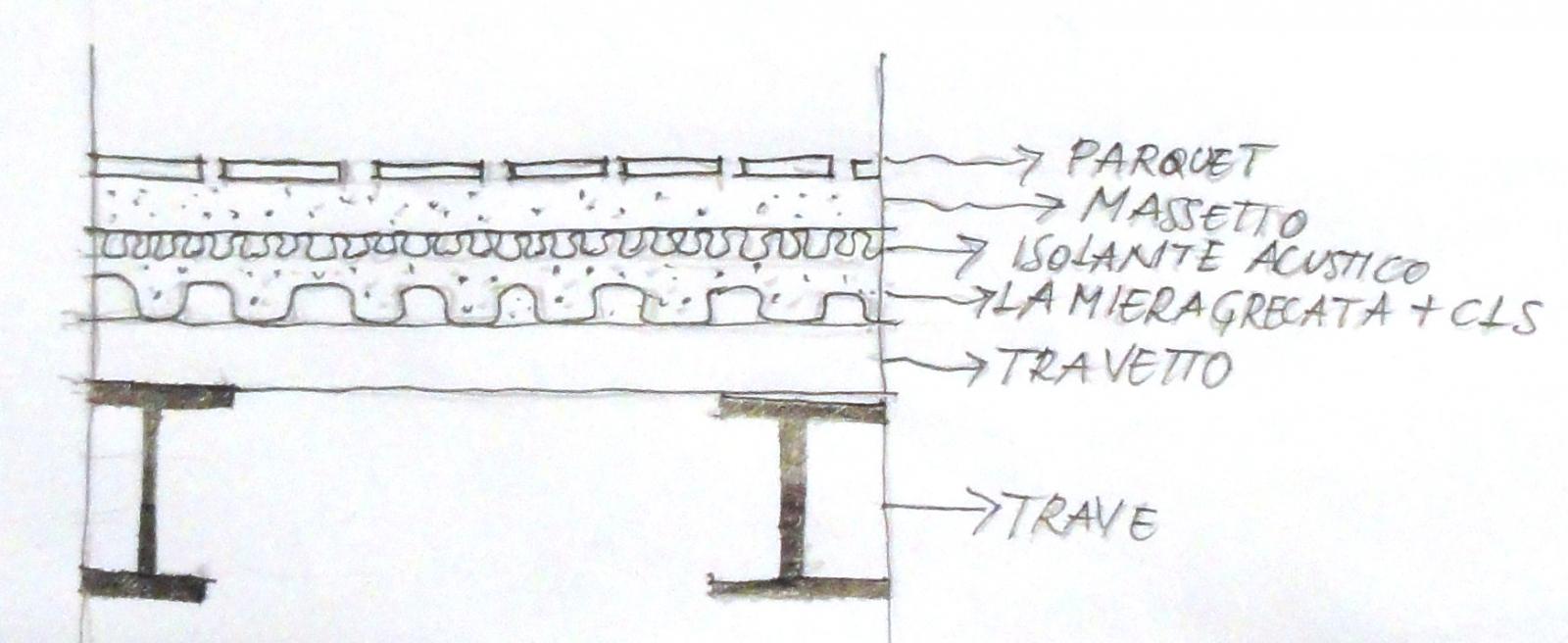
a) Dimensionamento del travetto (interasse 1m, luce 4m):

Partiamo con il dimensionamento del travetto prendendo come carico strutturale iniziale quello del    tavolato.

Qs:

- Lamiera grecata più getto in cls:

Spessore: 0,1 m   tipo: A55/P600 

 

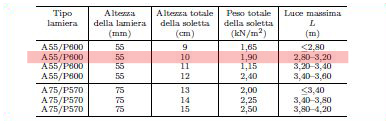
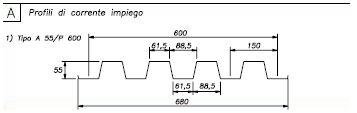
Come tabellato il peso a mq è 1,90 KN/mq

Qp:

-Isolante acustico  (Acustic system 7):

Spessore : 0,007 m

Peso a mq:  3 Kg/mq   0,03 kn/mq   (fornito dalla casa produttrice)

-Massetto in cls:

Spessore:  0,08 m

Peso specifico: 2000Kg/mc

Volume: 0,08 x 1 x 1 =0,08 mc

Peso: 0,08 x 2000 = 160 Kg   1,6 KN

Peso a mq: 1,6 kn/mq

-Parquet in ciliegio:

Spessore: 0,02 m

Peso specifico: 850 Kg/mc

Volume: 0,02 x 1 x 1= 0,02 mc

Peso: 0,02 x 850= 17 Kg    0,17 KN

Peso a mq: 0,17 KN/mq

-Incidenza impianti:

Peso a mq: 0,5 KN/mq

-Incidenza tramezzi:

Peso a mq: 1 Kn/mq

Qp tot: 0,03+1,6+0,17+0,5+1= 3,3 KN/mq

 

Qa:

-Civile abitazione:    2 KN/mq

Inseriamo i dati nella tabella excel

 

Scelgo un profilo IPE 140 con Wx= 77,3 cm^3  h=140 mm b= 73mm  Area= 16,4 cmq

Peso specifico: 7800 kg/mc

Volume: 0,00164 x 1  =0,00164 mc

Peso: 0,00164 x 7800= 12,79 Kg    0,1279 KN

Peso mq: 0,1279x 1/1= 0,1279 KN/mq

Qstot: carico soletta più carico travetto   0,1279+1,9=2,027 KN/mq

A questo punto abbiamo inserito nella tabella il nuovo Qs comprendente anche il peso dei travetti.

Ne risulta una trave con Wx pari a 71,71 cm^3, valore inferiore a quello proprio del travetto da noi scelto.

Il travetto è quindi verificato.

b) Dimensionamento trave

A questo punto possiamo inserire nella tabella la luce e l’interasse relativi alla trave (mantenendo gli stessi carichi).

Abbiamo scelto una trave IPE 330 con Wx= 713cm^3  A=62,6 cmq

Peso specifico: 7800 Kg/mc

Volume: 0,00626 x 1= 0,00626 mc

Peso: 0,00626 x 7800 = 48,8 Kg    0,488 KN

Peso mq: 0,488 x 1/4 = 0,122 KN/mq

Abbiamo sommato il peso a Qs  e aggiunto il nuovo valore alla tabella

Qs tot= 2,027 + 0,122 =2,149 KN/mq

Una volta inserito il peso della trave il nuovo Wx richiesto è di 656,15 cm^3, valore inferiore a quello relativo alla trave da noi scelta. Anche questa sezione è verificata.

 

Struttura in cemento armato

 

Qs:

-Pignatte:

Volume: 0,16 x 0,5 x 1= 0,08 mc

Peso specifico: 600 Kg/mc

Peso: 0,08 x 600= 48 Kg    0,48 KN

Peso mq: 0,48 KN/mq

-Travetti: 

Volume: 0,1 x 0,16 x 1 = 0,016 mc

Peso specifico: 2500 Kg/mc

Peso: 0,016 x 2500 = 40 Kg    0,4 KN

Peso mq: 0,4 KN/mq

-Soletta:

Volume: 0,04 x 1 x 1= 0,04 mc

Peso specifico: 2500 Kg/mc

Peso: 0,04 x 2500= 100 Kg    1 KN

Peso mq: 1 KN/mq

Qs tot: 0,48 + 0,4 + 1 = 1,88 KN/mq

Qp:

-Massetto in cls:

Spessore: 0,04 m

Peso specific0: 2000 Kg/mc

Volume: 0,04 x 1 x 1= 0,04 mc

Peso: 0,04 x 2000 = 80 Kg    0.8 KN

Peso mq: 0,8 KN/mq

-Isolante acustico  (Acustic system 7):

Spessore : 0,007 m

Peso a mq:  3 Kg/mq   0,03 kn/mq   (fornito dalla casa produttrice)

-Allettamento in cls:

Spessore:  0,03 m

Peso specifico: 2000 Kg/mc

Volume: 0,03 x 1 x 1 =0,03 mc

Peso: 0,03 x 2000 = 60 Kg   0,6 KN

Peso a mq: 0,6 kn/mq

-Parquet in ciliegio:

Spessore: 0,02 m

Peso specifico: 850 Kg/mc

Volume: 0,02 x 1 x 1= 0,02 mc

Peso: 0,02 x 850= 17 Kg    0,17 KN

Peso a mq: 0,17 KN/mq

-Intonaco:

Spessore: 0,01 m

Peso specifico: 1200 Kg/mc

Volume: 0,01 x 1 x 1= 0,01 mc

Peso: 0,01 x 1200= 12 Kg    0,12 KN

Peso a mq: 0,12 KN/mq

-Incidenza impianti:

Peso a mq: 0,5 KN/mq

-Incidenza tramezzi:

Peso a mq: 1 Kn/mq

Qp tot: 0,8+0,03+0,6+0,17+1+0,5+ 0,12= 3,22 KN/mq

Qa:

-Civile abitazione:    2 KN/mq

Inseriamo i dati nella tabella excel

Dalla tabella si ricava che, data una base di 25 cm, l’altezza minima deve essere di 38,68cm. Prendiamo una trave  25x45 con classe di resistenza C40/50 (e acciaio B450C per zona sismica).

Aggiungiamo ai carici strutturali a mq il peso a mq della trave P: 2,42 x 1/interasse = 0,605 KN/mq

Qs tot= 1.88 + 0,605= 2,48 KN/mq

Inserendo il nuovo dato nella tabella si ricava che l'altezza necessaria è pari a 40,08 cm, inferiore all’altezza della trave scelta. La nostra sezione è quindi verificata.

 

Seconda Esercitazione:

Travatura reticolare 3D

Per eseguire questa esercitazione abbiamo utilizzato Autocad e Sap 2000.

In Autocad ho disegnato la travatura reticolare composta da 4x6 moduli cubici(2x2)collegati da aste inclinate  nella stessa direzione.

Ho successivamente importato il 3D in Sap.

Per prima cosa assegno le cerniere interne a tutto il corpo e applico i 4 vincoli (cerniere) alle estremità della base

 

Ho in seguito definito il materiale e la sezione scegliendo una sezione tubolare in acciaio.

Definisco quindi un carico che chiamo “concentrato” di 40 KN verso il basso sull’asse Z e lo assegno ad ogni nodo della superficie superiore.

Dopo aver numerato le aste lascio analizzare la mia struttura dal sistema ottenendo così il diagramma dello sforzo normale.

Esporto i dati nella tabella excel prendendo in considerazione solo quelli relativi alla lunghezza totale delle aste dritte (2m) e inclinate (2,8m) essendo i dati relativi a sezioni eseguite in differenti punti della lunghezza totale.

Procedo riordinandomi i valori dello sforzo normale in ordine decrescente. Riesco così ad individuare immediatamente i valori massimi di trazione e di compressione.

Progetto e verifica a compressione per l’asta di 2 m

 

L’asta sottoposta a maggior sforzo di compressione è l’asta n. 189 con sforzo normale pari a 296,438 Kn.

So che σ=N/A ≤ Fd.  Per il progetto dell’asta ponendo  σ= Fd=N/A  ne risulta che, per trovare l’area della sezione, devo applicare la formula A=N/Fd dove Fd indica il valore di design che si calcola attraverso il rapporto tra Fy (valore della tensione di snervamento dell’acciaio) e γ (coefficiente di sicurezza che corrisponde a 1,05). Scelgo un acciaio FE 510 S 355 che ha un Fy di 3550 Kg/cmq

Fd=3550/1,05=3380,96 Kg/cmq = 33,8096 Kn/cmq.

A= 296,438/33,8096= 8,8 cmq

Cerco sulla tabella dei profilati tubolari in acciaio (tratta dal sito www.oppo.it) la sezione subito maggiore che è quella di 9,650 cmq

Per eseguire la verifica della sezione scelta dovrà risultarmi una σ<Fd

σ= 296,438 Kn/9,65 cmq = 30,72 Kn/cmq    Essendo 30,72 Kn/cmq< 33,8096Kn/cmq la sezione è verificata.

E’ ora necessario verificare che la sezione sia stata opportunamente dimensionata per evitare sbandamenti (instabilità Euleriana) e che resista quindi al carico critico Euleriano.

La formula per calcolare il peso critico è ^2 x E x Jmin)/lo^2 dove E è modulo di elasticità che per l’acciaio è 210000 N/mmq, Jmin è il momento d’inerzia della sezione scelta e lo è la lunghezza libera di inflessione che si calcola moltiplicando la lunghezza dell’asta per un coefficiente relativo ai tipi di vincoli applicati all’asta (nel nostro caso il coeff. è 1 trattandosi di un’asta doppiamente incernierata.

P crit= (3,14^2 x 210000 N/mm^2 x 87,90 cm^4)/ 40000 cm= 455014,35 N = 455,01435 KN

Essendo il peso critico maggiore dello sforzo normale, 455,01435 > 296,438, l’asta progettata non andrà in instabilità euleriana.

Progetto e verifica a compressione per l’asta di 2,8 m

L’asta sottoposta a maggior sforzo di compressione è l’asta numero 7 con sforzo normale pari a 307,351 KN.

σ=N/A ≤ Fd    Per il progetto dell’asta ponendo  σ= Fd=N/A  ne risulta che, per trovare l’area della sezione, devo applicare la formula A=N/Fd.

A=307,351Kn/ (338096 Kn/mq)= 9,091 Cmq

Scelgo una trave tubolare a sezione circolare con sezione metallica pari a 10,70 cmq.

Per eseguire la verifica della sezione scelta dovrà risultarmi una σ<Fd

σ= 307,351 Kn/10,7 cmq= 28,73 Kn/cmq       28,52 < 33,80 quindi la sezione è verificata.

Ora verificherò che anche questa  sezione sia stata opportunamente dimensionata e che quindi non sia a rischio sbandamenti.

Ricordo che la formula per calcolare il peso critico è (π^2 x E x Jmin)/lo^2 e sostituisco i miei valori.

(9.86 x (210000 N/mm^2) x96,30cm^2)/78400cm = 254335,18N= 254,335Kn

Il peso critico risulta inferiore al nostro sforzo normale, la sezione non è quindi verificata.

Prendo una sezione più grande. La verifica a compressione non è necessaria perché essendo la sezione maggiore della precedente, verificata a compressione, sarà sicuramente verificata anch’essa.

Scelgo una sezione con A=13,90cmq e Jmin=211cm^4

Passo di nuovo a verificare che non sia sottoposta ad inabilità euleriana.

Peso critico= 9,86 x( 210000 N/mm^2) x 211 cm^4/78400cm= 557266,072 N= 557,267Kn

Questa volta il Peso critico è maggiore del nostro sforzo normale; La sezione è quindi verificata anche per l’instabilità euleriana.

Ora procedo con il progetto e verifica a trazione.

Per il progetto e verifica  a trazione mi basterà progettare e verificare l'asta con lo sforzo a trazione maggiore dal momento che in questo caso non devo verificare le sezioni anche per il peso critico euleriano.

Inoltre avendo già progettato le aste per la compressione, mi basterà verificare che queste sezioni siano resistenti anche per lo sforzo di trazione.

In questo caso lo sforzo maggiore è sull'asta lunga 2,8m ed è pari a:256,572KN.

Dal precedente dimensionamento sul'asta di 2,8 metri avevamo un tubolare con: A=13,90cmq

Per cui per la verifica dovrò avere la σ=N/A ≤ Fd

σ = 256,572 Kn /13,90 cmq= 18,45 Kn/cmq < 33,88 Kn/cmq (che è il mio Fd)

La sezione è quindi verificata a trazione.

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------