FATAL ERROR... non riesco più a modificare il mio blog quindi sto riportando quello vecchio qua..

TRAVE RETICOLARE SIMMETRICA

 

Le travi reticolari sono composte da aste rettilinee, collegate alle estremità mediante cerniere, soggette solo a sforzo normale.

 

 

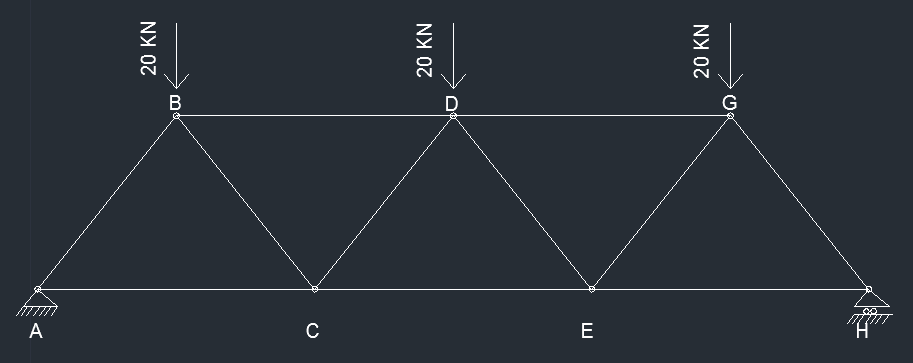
STEP 1 VERIFICA DELL'ISOSTATICITA'

 Per verificare se la struttura è isostatica dobbiamo vedere se il numero dei vincoli è uguale al numero dei gradi di libertà della struttura. V sarà uguale alla somma dei vincoli interni più quelli esterni. Quelli esterni sono facili da individuare, sono 3, quelli interni li calcoliamo con una piccola formula: V_i = 2*(n -1) dove n è il numero di aste che arrivano alla cerniera interna.

Per ogni cerniera avremo:

 

A-H     2*(2-1) = 2

B-G     2*(3-1) = 4

C-D-E     2*(4-1) = 6  La somma dei vincoli interni è 30 quindi V= 33.

Ora bisogna confrontare il n. dei vincoli per i gradi di libertà della struttura (numero di aste presenti nella struttura X per il numero di gradi di libertà di ogni elemento)

V= 33 L =33 la struttura è ISOSTATICA!

STEP 2 CALCOLO DELLE REAZIONI VINCOLARI.

Considerando che la struttura è simmetrica le reazioni saranno anch'esse simmetriche.

Equilibrio alla traslazione verticale: V_A + V_B - 60 kN = 0

Va= 30 KN; Vb= 30 KN

STEP 3 CALCOLO DELLE AZIONI DI CONTATTO CON IL METODO DELLE SEZIONI DI RITTER

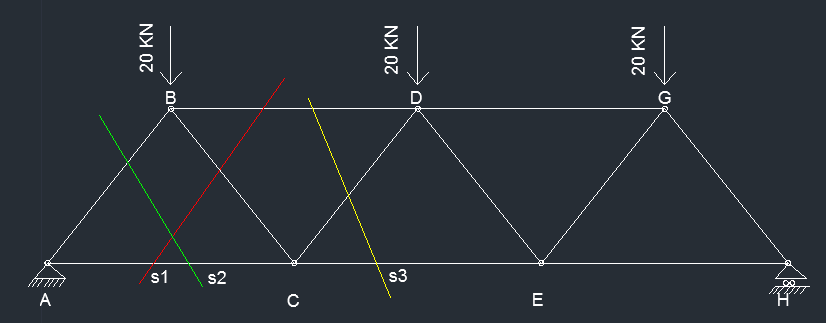
Calcolo gli sforzi lungo le aste usando il metodo delle sezioni di RITTER. Taglio la struttura in più parti tramite sezioni che prendono un numero di aste che non concorrono nello stesso modo; poi si dovrà vedere se le aste saranno soggette a compressione o trazione ( N>0 TIRANTE), (N<0 PUNTONE)

SEZIONE N 1

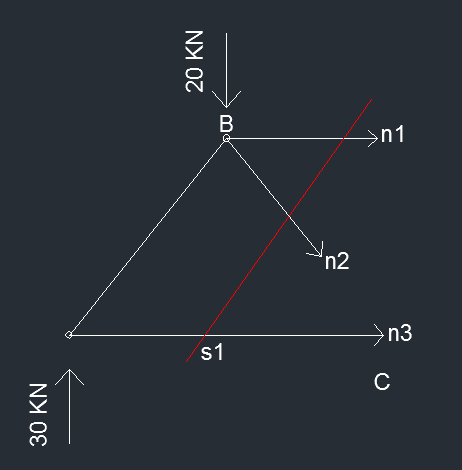
Faccio l'equilibrio dei momenti intorno a C

∑M (c) = 0      -30KN X 4m + 20KN X 2m - N₁ X 2m = 0

N₁ = -40 KN (negativo è un PUNTONE)

Per trovare N₃   faccio l'equilibrio intorno a B

∑M(b) = 0     -30KN x 2m + N₃ x 2m =0    N₃ = 30KN (positivo è un TIRANTE)

Per trovare N₂  lo scompongo come se fosse la diagonale di 1 quadrato.

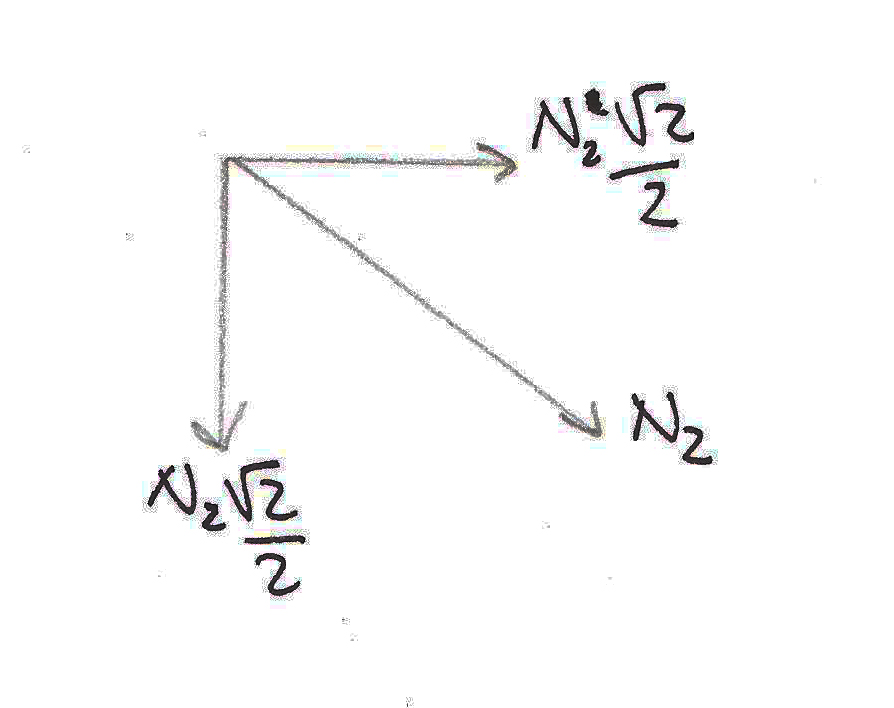
∑y= 0    30KN -20KN - N₂ √2/2 = 0  N₂ = 10√2 KN ( N>0 )

SEZIONE N 2

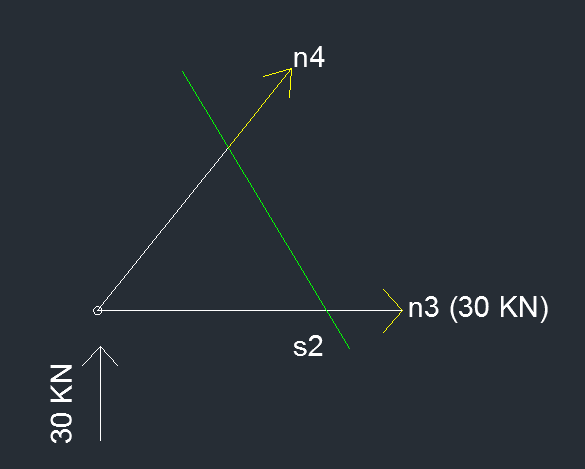
∑y= 0    N₃ + N₄ √2/2 = 0        30KN + N₄ √2/2= 0   N₄ = -30√2 KN

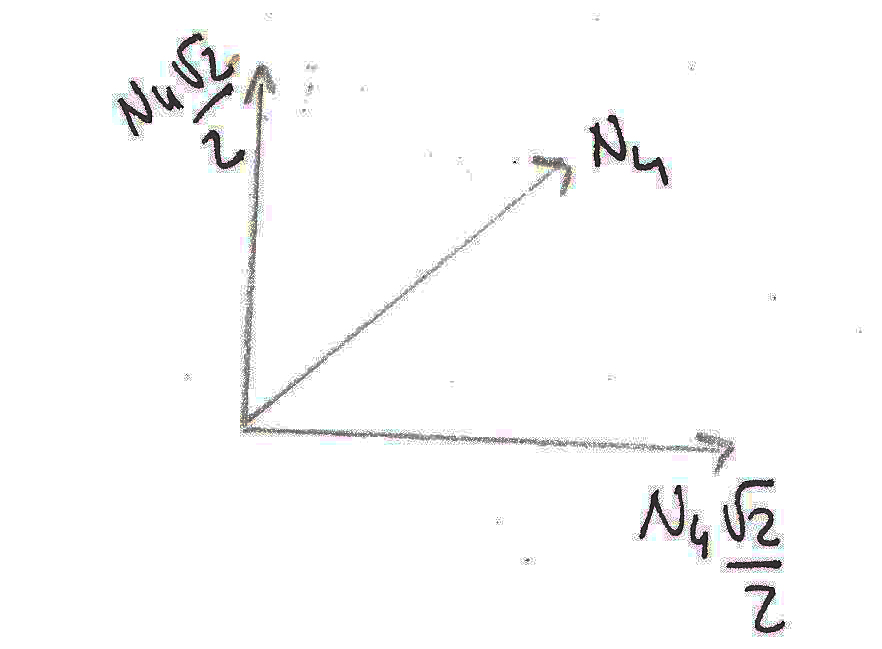
SEZIONE N 3

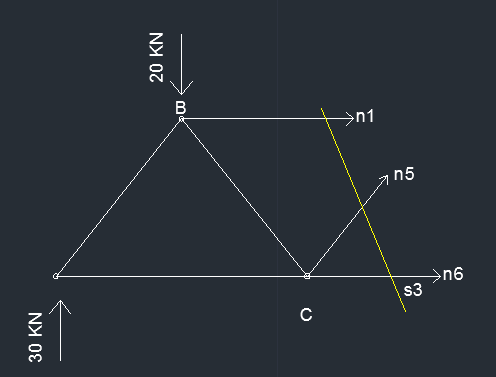
∑M(d) = 0         N₆  x 2m + 20KN x 4m - 30KN x 6m = 0     N₆ = 50 KN

Trovo N₅       

∑y =0         30KN- 20KN + N₅ √2/2 = 0       N₅ = -10 √2 KN

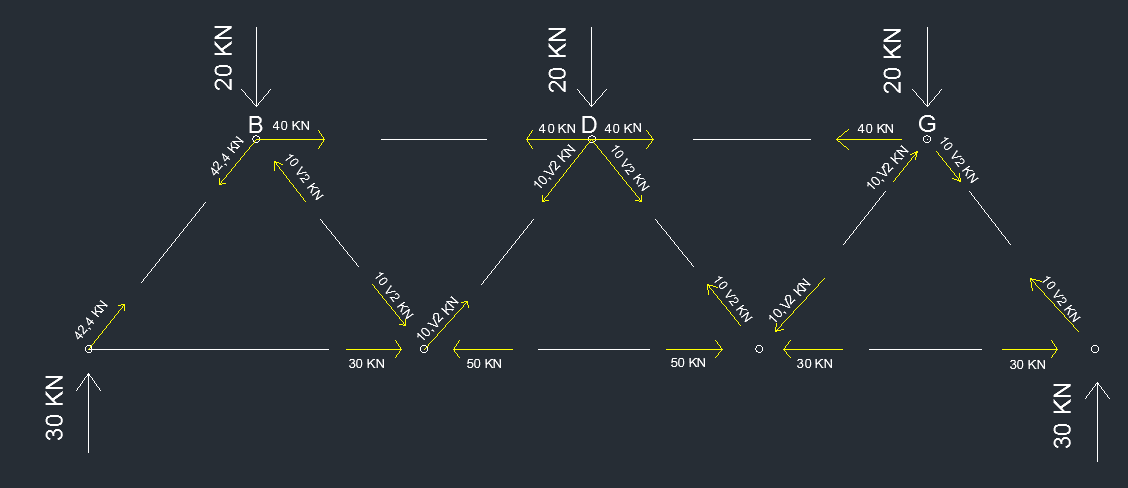
disegno tutte le reazioni nelle aste.

STEP 4 ANALISI IN SAP

Una volta impostete le unità di misura (Kn m C) mi apro la trave reticolare del modello predefinito (n campate 3, ampiezza 2 altezza 1).

Definisco il materiale (DEFINE - MATERIAL -ADD NEW MATERIAL) e la geometria ( TUBOLARE) e assegno il materiale appena creato alla nostra struttura.

Ora la carico nei nodi 5 -6- 7 e faccio partire l'analisi.

la sua deformata

e i rispettivi diagrammi N,T,M

TRAVE RETICOLARE ASIMMETRICA

In questo esercizio la trave reticolare è asimmetrica e lo affronteremo, a differenza dell'altro, con il metodo dei nodi.

Come sappiamo una struttura è in  equilibrio se ognuno dei suoi nodi lo è. Facciamo quindi per ciascuno di essi l'equilibrio a traslazione.

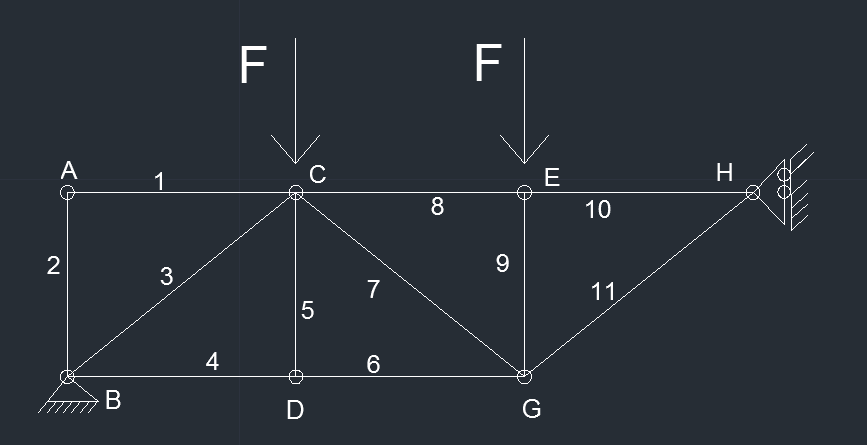
Anche qua mi assicuro che la struttura sia isostatica, dopo di che mi trovo le reazioni vincolari.

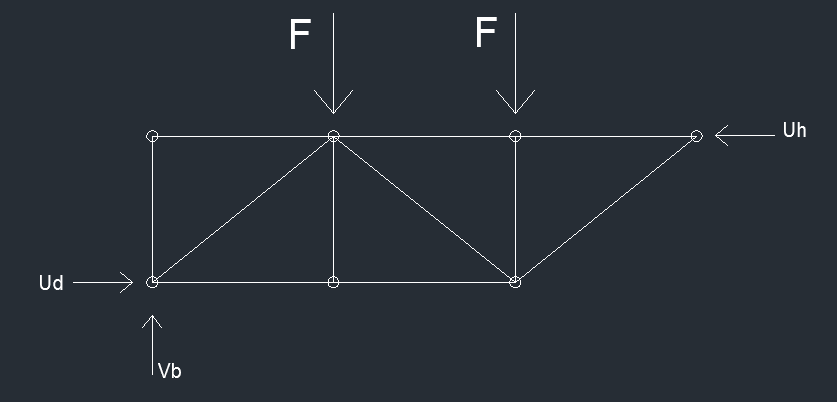
 Equilibrio alla traslazione orizzontale

U_B - U_G = 0 ------------- U_B = U_G

 Equilibrio alla traslazione verticale

V_B - 2F = 0 -------------- V_B = 2F = 20 kN

- Equilibrio alla rotazione in B

- F*l - F*2l + U_G*l = 0 ----> U_G = 30 kN = U_B

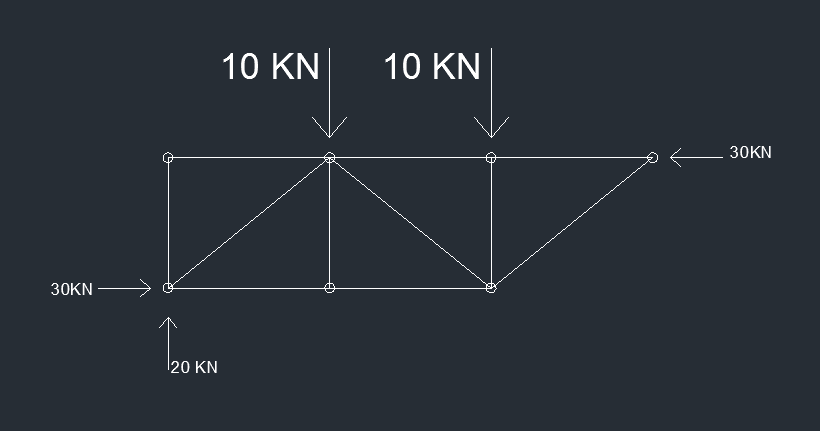
Ora bisogna isolare ogni nodo e calcolarne l'aqeuilibrio.

NODO A

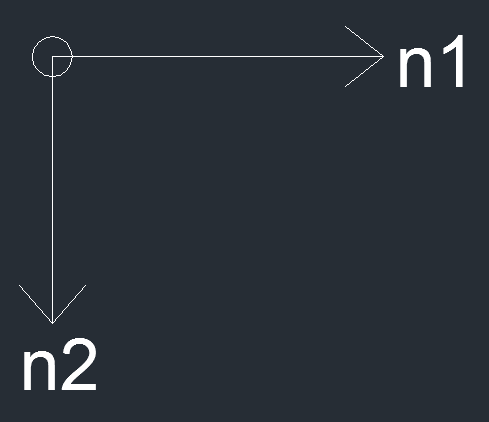
 Equilibrio alla traslazione orizzontale N₁ = 0

 Equilibrio alla traslazione verticale N₂ = 0

NODO B

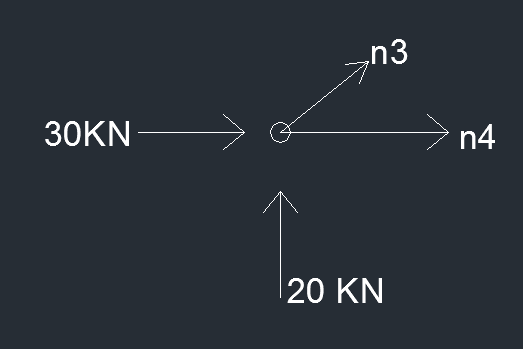
 orizzontale 30 kN + N₄ + N₃* √2/2 = 0

 verticale 20 kN + N₃* √2/2 = 0 ----> N₃ = -20√2 kN

N₄ = - 10 kN

NODO D

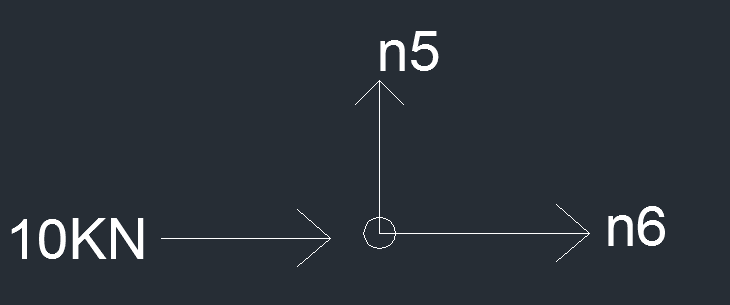
 orizzontale 10 kN + N₆ = 0 ----> N₆ = 10 kN

 verticale N₅ = 0

NODO C

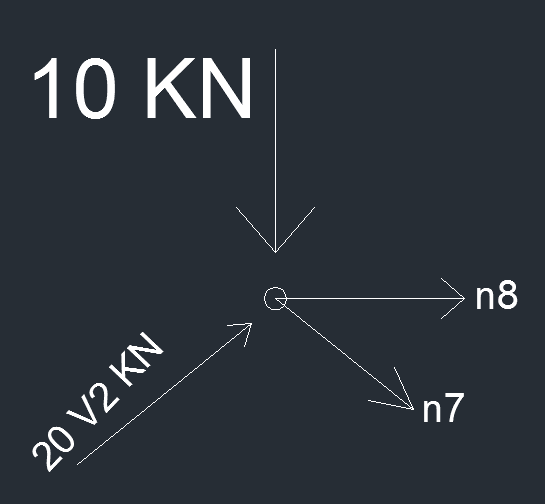
orizzontale 20 kN + N₈ + 10 kN = 0 ----> N₈ = -30 kN

 verticale 20 kN - 10 kN - N₇*√2/2 = 0 ----> N₇ = 10√2 kN

NODO G

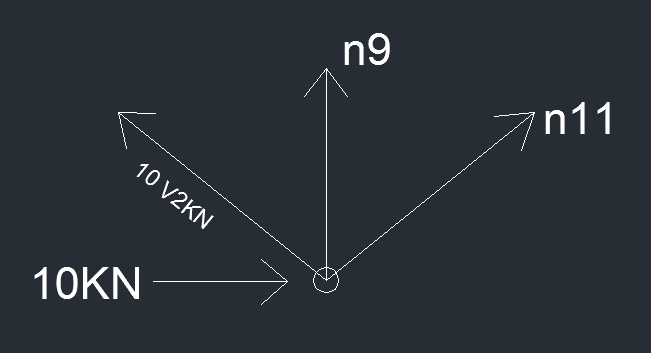
orizzontale 10 kN + N₁₁*√2/2 - 10 kN = 0 ----> N₁₁ = 0

 verticale N₉ + 10 kN = 0 ----> N₉ = -10 kN

NODO H

 

orizzontale N₁₀ = - 30 kN

 

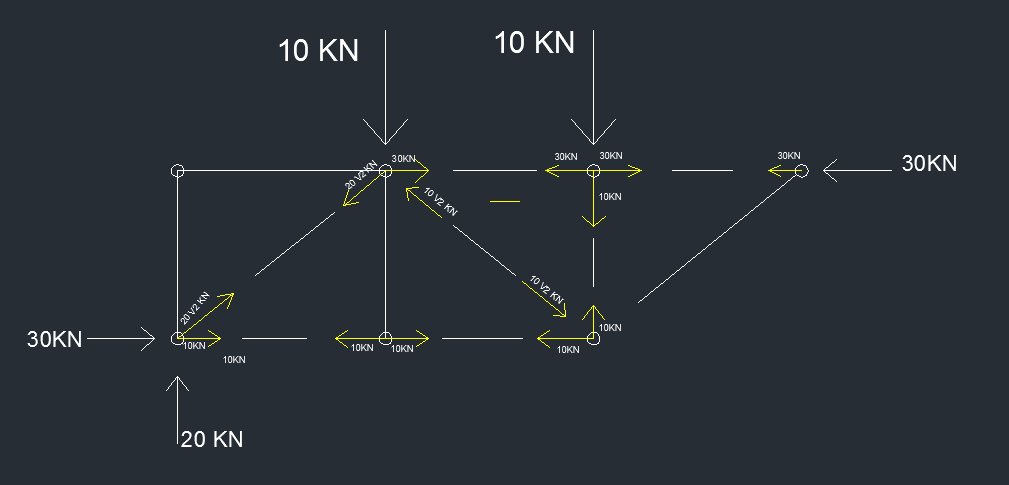
disegno tutti gli sforzi assiali per ogni asta, verifico in sap, e ottengo il mio diagramma delle N.

 

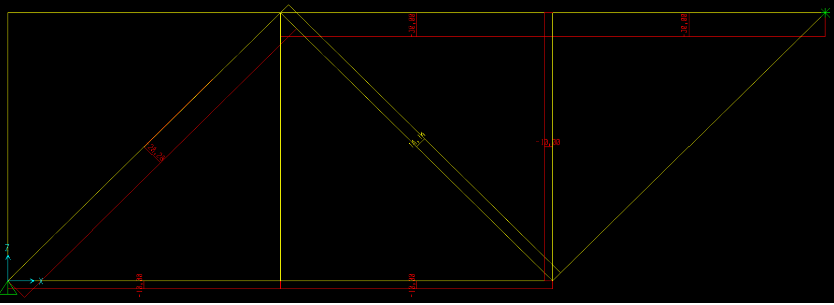
ESERCIZIO IN CLASSE

CALCOLO DELLE REAZIONI VINCOLARI:

Primo corpo

∑y=0       ya+yb=0   ya= -yb

∑M(a)=0    -50+yb x 6m    yb= 50/6 = 8,33    quindi  ya= -8,33

Secondo corpo

∑y= 0       -yb+yc=0    yb=-yc

∑M(b)=0    50 + Yc x 6m=0     yc= -8,33  quindi yb= 8,33

verifica in sap....

DIMENSIONAMENTO TRAVE IN CLS, LEGNO ACCIAIO.

PROGETTO A FLESSIONE

L'esercitazione verte nel dimensionare una trave (o travetti) in tre diverse tipologie con l'aiuto del nostro foglio exel.

Tutto ruota intorno alla formula di flessione (che può essere utilizzata come formula di verifica o di progetto)

                       σ = Mx      y

                          -------

                              Ix

 

Dove Mx è il momento flettente che agisce sulla sezione che la fa ruotare intorno all'asse x, Ix è il momento principale di inerzia intorno all'asse x e y è una variabile che varia sulla sezione.

Questa formula ci fa capire come nel materiale arriva la TENSIONE per effetto della flessione, cioè da l'indicazione, data una sezione, dell'andamento della tensione media.

A noi interssa però la σ max= Mx /Wx  dove Wx= Mx/ fd.

Nel momento in cui faccio il progetto di una sezione, impongo che la tensione massima sia proprio il valore che mi ha datola normativa in funzione del materiale che ho scelto.

fd è il valore di progetto della tensione massima del materiale che è legato al valore di crisi (la crisi va distinta da maeriale a materiale). Noi dobbiamo prendere distanza da questa crisi, grazie ai coeficienti di sicurezza che variano da materiale a materiale.

 

Le formule presenti in exel partono da dati ben precisi: LUCE DELLA TRAVE, MATERIALI E CARICHI.

Utilizziamo le formule come equazione. Tutti i dati che inseriamo nel foglio serviranno ad eliminare un'incognita, perchè abbiamo una sola equazione.

Questa incognita per la sezione di legno sarà L'ALTEZZA, per l'acciaio sarà il MODULO DI RESISTENZA A FLESSIONE  e per il cls sarà L'ALTEZZA UTILE.

 

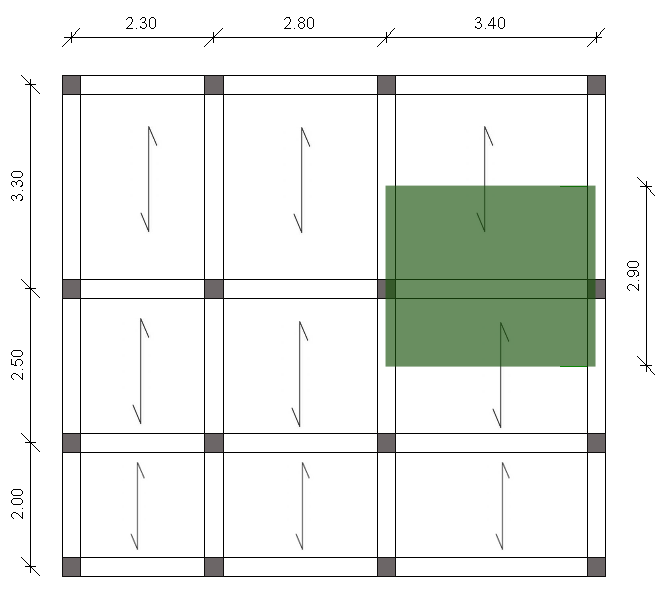
L'impalcato in esame è un'abitazione ad uso residenziale.

ACCIAIO

DIMENSIONAMENTO TRAVETTI:

Luce della campata maggiore: 3,30 m

Interasse: 1 m

 

ANALISI DEI CARICHI: per progettare la sezione dobbiamo definire i carichi.

 

 - VARIABILI

Sovraccarichi accidentali Qa (legati alla funzione dell'edificio)  - un'abitazione ad uso residenziale 2KN/mq

Riporto qui la tabella con le categorie dei tipi di locali previste dalla normativa per la definizione di tali carichi.

 

 

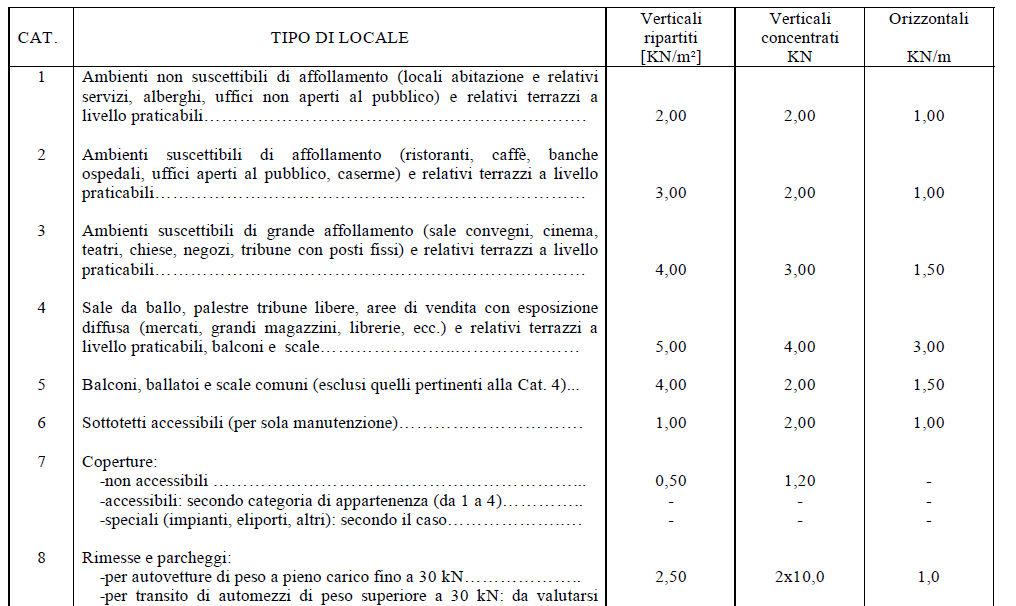
- PERMANENTI

Sovraccarichi di natura permanente: Qp ( carico esercitato sulla struttura dal peso degli elementi costruttivi fissi all'interno del solaio)

                                     - pavimento in gres porcellanato 0,2 KN/mq

                                        - massetto 0,64 KN/mq

                                        - isolante 0,00072 KN/mq

                                        -  incidenza impianti che è 0,50KN/mq

                                        - incidenza tramezzi 1KN/mq

 

Pesi propri delle sturtture: Qs (peso proprio della struttura)  - soletta e la lamiera grecata (10 cm)1,86KN/mq

 

 

 

 

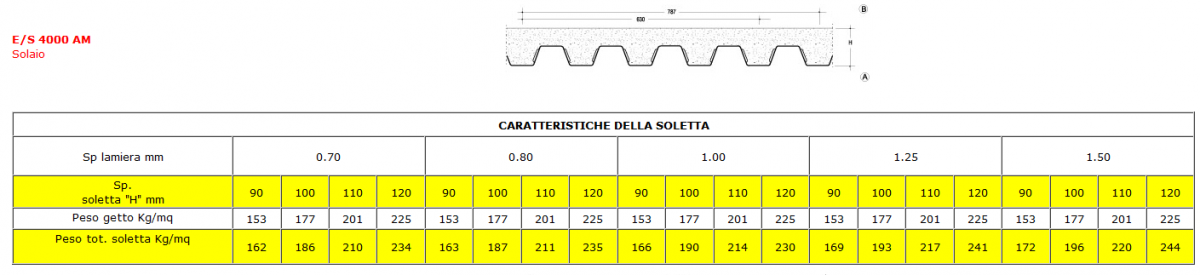
Per trovarmi il carico totale al metro lineare farò: Qa + Qp + Qs x 1 m = 6,21 KN/mq

 

Utilizzo il foglio excel per trovarmi Wx ovvero il modulo di resistenza che mi indicherà il tipo di profilo da utilizzare per i miei travetti.

 

 

Wx = 37,77 cm ³

 

 

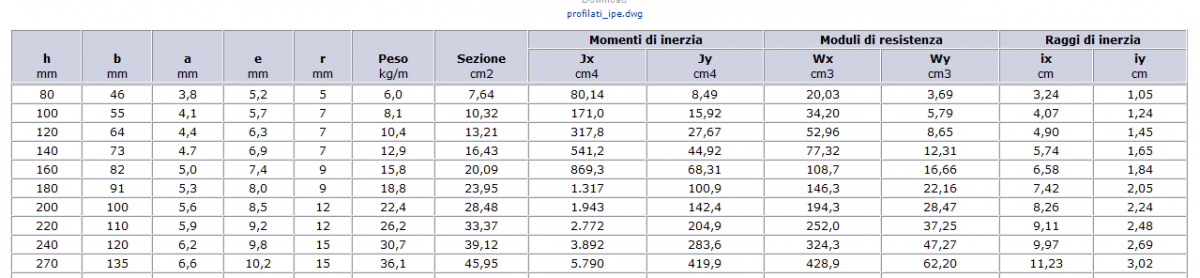
N.B. Nel foglio exel c'è una differenza tra caselle azzurre e bianche. In quelle azzurre dobbiamo NOI mettere i dati, mentre le bianche ci danno il risultato. La colonna E ci da il risultato del Q totale, ottenuto moltiplicando la somma di Qa + Qs + e Qp per l'interasse, per trasformare il carico al mq in carico lineare. Nella colonna G compare il nostro momento massimo (per la trave appoggiata ql / 8, ma si può sempre cambiare la formula). Nella colonna H troviamo la classe di snervamento dell'acciaio che abbiamo scelto. Colonna I c'è il valore di progetto Fd.

 

 

 

Secondo la tabella devo utilizzare una IPE 120 con un peso di 0,104 KN/mq. Ora devo verificare che il modulo di resistenza che viene, sommando il Q con il peso dell'ipe, non sia superiore al modulo di resistenza dell'ipe stessa.

 

0,104 KN/mq + 6,21 KN/mq = 6,314 → Wx = 38,40 ‹ 52,96 LA VERIFICA è SODDISFATTA!

 

DIMENSIONAMENTO TRAVE PRINCIPALE:

 

 

Luce: 3,40 m

Interasse: 2,90 m

Qa: 2 KN/mq

Qs: 1,964 KN/mq (1,86 + 0,104 KN/mq)

Qp: 2,3472 KN/mq

 

Wx= 118,17 cm³ → IPE 180 che pesa 18,8 kg/m

 

Q + 0,188KN/mq = → Wx = 119,12 m³ < 146,3 m³ LA VERIFICA è SODDISFATTA

 

LEGNO

 

DIMENSIONAMENTO TRAVETTI:

 

Luce : 3,30 m

 

Interasse: 0,5 m

 

Qa: 2 KN/mq

 

Qs: tavolato: 350 kg/m³ (legno forte) x 0,035 m (spessore) = 12,25 kg/mq → 0,1225 KN/mq

 

Qp: pavimento (cotto 28 kg/mq) 0,28KN/mq; massetto (1800kg/mc x 0,05 m) 0,9KN/mq; impianti 0,50KN/mq e incidenza tramezzi: tramezzo 8 cm, intonaco 1 cm; peso specifico laterizio 800 kg/mc x 0,08m = 0,64KN/mq – peso specifico intonaco 2000 kg/mc x 0,01m = 0,2 x2 (intonaco da entrambe le parti del tramezzo) = 0,4 KN/mq

 

TOTALE TRAMEZZI: 0,64KN/mq + 0,4 KN/mq x H (altezza) / i (interasse) = 1,07 KN/mq

 

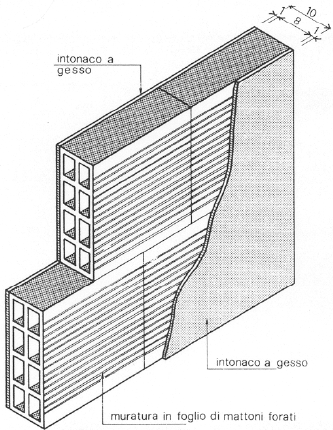
Qa + Qs + Qp = 2,32KN/mq

 

Inserisco i dati nel foglio excel e ipotizzo la base del mio travetto di 10 cm, otterrò un h di 15,13cm.

L'altezza che ho ottenuto la più piccola altezza della sezione della trave.

Quindi scelgo una sezione di 10x16 e un legno GL24h. Ora devo aggiungere il peso del travetto al Q e verificare che la nuova altezza risulti entro i limiti di quella ipotizzata.

 

Il legno GL 24h ha una massa volumica di 380Kg/m³, quindi per un travetto di 10x16cm avrò:

3,8KN/mc x 0,1m x 0,16m x 1m = 0,060KN/m x 2 (perchè in un metro ci sono due travetti) = 0,12 KN/m

Sommando il peso del travetto al Q iniziale ottengo un h di 15,52 che è < di 16 quindi la VERIFICA è SODDISFATTA!!

 

 

N.B nel valore di progetto del legno troviamo un coefficiente moltiplicativo Kmod ,che tiene conto dello scorrere del tempo,(molto basso tipo 0,7-0,6 0,5) in funzione della durata del carico. Se il carico in cui staimo facendo la verifica è permanente, stiamo ammettendo che quel legno deve durare 40-50 anni.

 

Fd = Kmod  Fk/ γ m → Kmod e γ m hanno lo stesso effetto: γ m essendo > 1 e stando al denominatore DIMINUISCE la resistenza, Kmod stando al numeratore e < 1 DIMINUISCE anch'esso la resistenza. Quindi Fk (che è il valore di crisi) viene abbattuto due volte.

 

DIMENSIONAMENTO TRAVE PRINCIPALE:

 

Luce: 3,40 m

 

Interasse: 2,9 m

 

Qa: 2KN/mq

Qp: 2,75 KN/mq

Qs: 0,1225 KN/m + 0,12KN/m = 0,2425KN/mq

 

Dal foglio excel, ipotizzando una base di 25 cm ho un h di 28,02 cm. Scelgo quindi una sezione di 20x30cm

Il legno GL 28h ha una massa volumica di 410 kg/m³. Mi calcolo il suo peso: 4,1KN/mc x 0,2m x 0,3m x 1m = 0,246 KN che vado a sommare a Q. Di seguito avrò la nuova h che è di 28,26cm < a 30 cm. LA VERIFICA è SODDISFATTA.!!