Progetto delle aste della piastra reticolare spaziale.

PROGETTO DELLE ASTE PIU' SOLLECITATE

Per prima cosa apro la tabella in Sap e vedo l' asta con il maggior sforzo di compressione e quella con  maggior sforzo di trazione.

Nmaxcompressione = 307,254 KN (asta n 161)

Nmax trazione = 263,469 KN (asta n 35)

La seconda cosa da fare è scegliere il tipo di acciaio con cui andrò a realizzare le aste. Fe 430 S275 (con tensione di snervamento di 275 MPa).

Prima di tutto si ottiene la tensione ammissibile facendo il rapporto fra la tensione di snervamento e il coefficiente di sicurezza di 1,05 (coefficiente di sicurezza dell'acciaio da carpenteria)

 In fase di progetto considero Fd = Fy/ γm = 275 / 1,05 = 261,90 MPA

La formula che domina lo sforzo normale è  σ = N/A . Questo vuol dire che se uno vuole contrastare lo sforzo normale deve avere un'area adeguata.

Mi devo chiedere quindi: qual'è l'area minima che ci devo mettere per stare in sicurezza.

σ = Fd = N/A -------   Amin = N/ Fd 

- PROGETTO A COMPRESSIONE

A = Nmax(compressione)/fD = 307254 N/261,9 N/mm² = 1173,172 mm² = 11,73 cm²

Dal mio profilaio scelgo un'area maggiore di quella appena trovata.

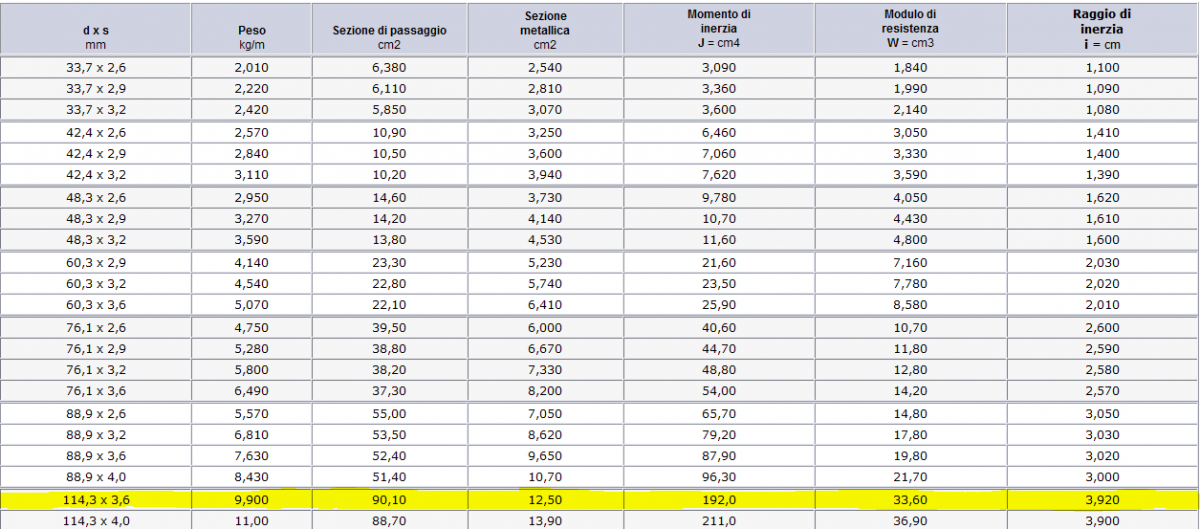
Area = 12,50 cm²

Diametro = 13,97 cm

Spessore = 2,9 mm

VERIFICA A COMPRESSIONE:

Dobbiamo verificare che lo sforzo normale di compressione sia MINORE del carico critico.

L'instabilità Eureliana è quel fenomeno per il quale se prendo un asta che ha un carico di punta (P) applicato alla testa, e questo carico supera una certa soglia, l'asta tenderà a sbandare perchè troppo SNELLA. (snellezza: rapporto tra altezza e lunghezza)

P> Pcritico ---- se il carico di punta P è maggiore di Pcritico la struttura è INSTABILE e il fenomeno si innesca.

Al contrario se P< Pcritico la struttura è STABILE.

Il carico critico si trova tramite questa formula:

Pcrit = (∏²  x  E x Jmin) / l₀²

E = modulo elastico dell' acciaio

 Jmin = momento d’inerzia minore

 l₀ = lunghezza libera d' inflessione (lunghezza dell’asta inclinata, quella soggetta a massimo sforzo normale)  2,828m

Pcrit = (3,14² * 210000N/mm² * 1920000 mm⁴) / 2828² mm = 497073N = 497,586 KN

Nmax 307,254KN < Pcritico 497,586 KN la VERIFICA è SODDISFATTA!!!

PROGETTO A TRAZIONE

A = Nmax(trazione)/fD = 263469 N/261,9 N/mm² = 1006 mm² = 10,06 cm²

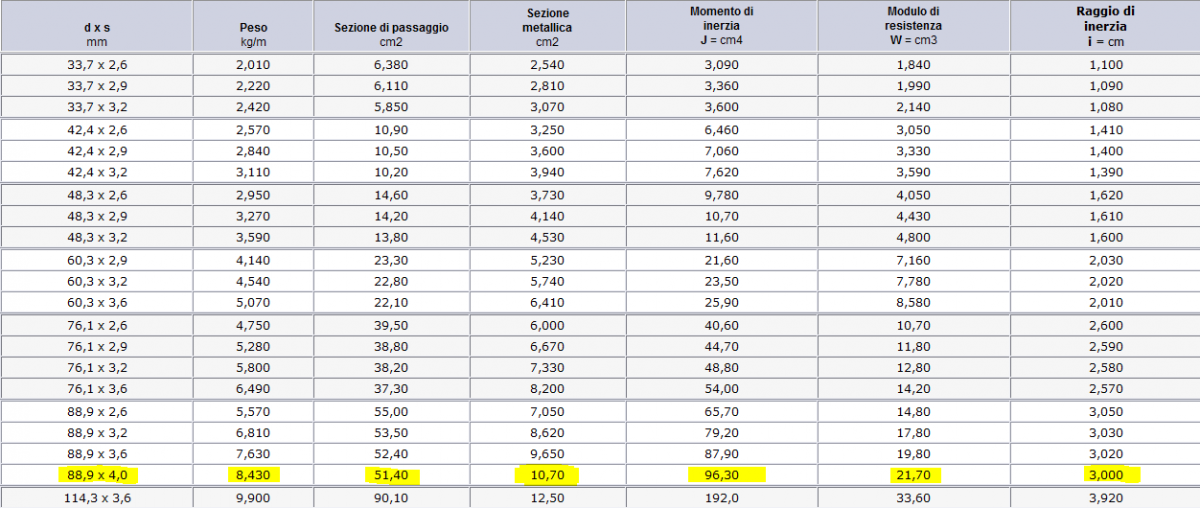
DIAMETRO =  8,89 cm

SPESSORE = 4 mm 

AREA =10,7 cm².

VERIFICA A TRAZIONE

Devo verificare che lo sforzo normale non faccia rompere la sezione.

σ = N/A < Fd ------------------- σ = 263469 N/ 1006mm² = 261,89 Nmm²   <   261,90 MPA

LA VERIFICA è SODDISFATTA!!