blog di Sotirios_Moschovitis

Visto che non era stato possibile pubblicare l'esercizitazione direttamente sul portale, si può trovare il file pdf con la presentazione in allegato.

In questa esercitazione è previsto il dimensiomaneto e la verifica di deformabilità della mensola più sollecitata di un solaio in tre diverse tecnologie, legno, acciaio e cemento armato.
Come nelle esercitazioni precedenti sarà utilizzato un foglio excel, diviso prima nella parte di Stato Limite Ultimo (SLU) e poi in Stato Limite di Esercizio (SLE) che si usa per i valori di spostamento e deformabilità della mensola.

CALCESTRUZZO ARMATO

 

Nella mia struttura di ipotesi, la mensola maggiormento sollecitata è quella al centro con luce 6m e un interasse 6m.
Il solaio utilizzato è lo stesso con l'esercitazione di prima, quindi i valori dei carichi (strutturale, permanente, accidentale) sono gli stessi.
Per trovare il valore di carico limite ultimo dobbiamo moltiplicare ogni carico con il suo coefficiente di sicurezza.
Ottenuto il valore del carico ultimo, è ora possibile trovare il momento massimo, utilizzando la formula ql2/2, per una mensola di lunghezza l sottoposta ad un carico q.

Per progettare la trave scegliamo un calcestruzzo con resistenza fck= 60 MPa insieme con un acciaio di armatura caratterizzato da una resistenza a flessione caratteristica fyk= 450 MPa.
Fatto questo possiamo calcolare le tensioni di progetto dell'acciaio fyd e del cls fcd. Dobbiamo poi impostare la base della trave da calcolare e la dimensione del copriferro per ricavare l'altezza utile e l'altezza minima.
Scegliamo una base di 30 cm e un copriferro di 5 cm, arrivando ad una altezza minima di 35 cm.
Dato che questa sia l'altezza minima, scegliamo un'altezza di 40 cm, ottenendo una trave di sezione 30 x 40 cm.

L'utilizzo di questi dati permette di ricavare l'area e il peso della trave, valori che servono per il calcolo del carico nello SLE, dove il cemento armato ha un peso non trascurabile.
Inserendo i dati e il modulo elastico E otteniamo il valore del carico allo SLE qe, il momento d'inerzia Ix e lo spostamento massimo Vmax = 0.27 cm.
Questo valore conferma il progetto, sapendo che il rapporto tra il momento d'inerzia e lo spostamento è maggiorte di 250
 Ix/ Vmax >250

 

ACCIAIO

Per progettare la nostra trave in acciaio viene scelto un'acciaio S235 con resistenza a flessione caratteristica fyk= 235 MPa
Dato questo è possibile calcolare la tensione ammissibile di progetto fd e il modulo di resistenza Wx minimo 452 cm3.
Scegliamo una IPE 300 con modulo di resistenza Wx= a 557.1 cm3, momento d'inerzia Ix = 8356 cm4 e peso = 42.2 kg/m.
Inserendo i dati e il modulo elastico E = 210000 MPa, otteniamo i valori del carico allo SLE che tiene conto anche del peso proprio della trave e dello spostamento massimo Vmax= 0.171 cm.

        
Questo valore conferma il progetto, sapendo che il rapporto tra il momento d'inerzia e lo spostamento è maggiorte di 250
 Ix/ Vmax >250

 

LEGNO

Per il progetto della nostra trave scegliamo un legno lamellare GL24H, con resistenza a flessione caratteristica fmk= 24 MPa. Scegliamo anche un coefficiente kmod= 0.8 e come coefficiente parziale di sicurezza del materiale γm= 1.45 
Fatto questo è possibile calcolare la tensione ammissibile di progetto fd.

Dobbiamo poi impostare la base della nostra trave per ottenere l'altezza minima.
Scegliamo una base di 25 cm e otteniamo un'altezza minima di 38.73 cm. Dato che questo sia il valore minimo dell'altezza della trave otteniamo una trave di sezione 25 x 40 cm.
Dopo aver fatto la parte relativa allo SLE, inseriamo il valore del modulo elastico del legno E= 8000 MPa, che non tiene però in considerazione il peso proprio della trave (il legno è un materiale leggero), del momento d'inerzia Ix e dello spostamento massimo Vmax= 0.41 cm.
Questo valore conferma il progetto, sapendo che il rapporto tra il momento d'inerzia e lo spostamento è maggiorte di 250
 Ix/ Vmax >250

 

 

La seconda esercitazione prevede il dimensionamento della trave maggiormente sollecitata da individuare nella mia carpenteria di ipotesi, ipotizzando l'utilizzo di tre tipologie per il solaio : calcestruzzo armato, acciaio e legno.

La trave è quella compresa tra i pilastri B1 e B2 avendo i seguenti dati:

l (luce) = 6.05 m

i (interasse) = 6.05 m

A (area d'influenza) = 6.05 x 6.05 = 36.60 mq

 

Per proseguire con il dimensionamento  devo prima calcolare il peso totale dei carichi che agiscono nella mia struttura ipotizzata, per poter determinare il carico lineare di progetto sulla mia trave maggiormente sollecitata.

Facendo riferimento alla normativa NTC D.M. 14/01/2008 posso individuare tre carichi:

- carico strutturale qs [kN/mq], cioè l'insieme dei carichi di tutti gli elementi costitutivi della mia struttura

- carico permanente qp [kN/mq], cioè l'insieme dei carichi di tutti gli elementi che compongono agiscono al solaio (impianti, pavimenti, tramezzi, intonaco, pavimento ecc.)

- carico accidentale qa, che indica carichi che agiscono non costantemente nella mia struttura, avendo un valore fissato in base alla destinazion d'uso dell'edificio. Nella mia esercitazione progetto un edificio ad uso residenziale, quindi il qa = 2kN/mq

Sempre in riferimento con la normativo devo utilizzare coefficienti (γG1, γG2, γQ1) per i rispettivi carichi. Facendo un analisi allo S.L.U. (Stato Limite Ultimo) sono coefficienti di sicurezza.

qu = γG1 x qs + γG2 x qp + γQ1 x qa

Questo serve per poter ricavare il momento massimo che agisce sulla mia trave, che per la mia esercitazione considero come una trave doppiamente appoggiata per cui il momento massimo ha valore 

e si trova alla metà.

 

CALCESTRUZZO ARMATO

 

Per la trave in cls armato ho scelto il solaio del modello UNI SOL - 03 che ha i seguenti carichi

Carico strutturale qs = 2.1 kN/mq

Carico permanente qp = 1.79 kN/mq

Essendo un materiale disomogeneo, il solaio di cls armato ha diversi classi di resistenza per l'acciaio (fyk) e il cls (fck), che mi servono per trovare la mie tensioni di progetto.

fyk = fyk/γs , γs : coefficiente di sicurezza dell'acciaio (=1.5)

fyd = acc x fck/ γc, acc : coefficiente riduttivo della resistenza a lunga durata del cls (=0.85)

                              γc : coefficiente di sicurezza del cls (=1.5)

Per poter ricavare l'altezza utile hu devo prima fissare il valore della base della mia sezione.

Determinata l'altezza utile, posso ricavare l'altezza minima che mi serve per scegliere la mia altezza di progetto.

 

Devo poi introdurre il peso proprio della mia trave nella sezione dimensionata per verificare che la mia altezza di progetto si verifica o se ho bisogno di aumentarla.

Se il risultato è minore rispetto alla mia altezza di progetto la mia sezione è verificata.

 

 

ACCIAIO

Per la trave in acciaio ho scelto il solaio UNI SOL -15 con i seguenti carichi:

Carico strutturale qs = 2.11 kN/mq

Carico permanente qp = 1.59 kN/mq

La prima operazione è quella di scegliere il materiale da utilizzare, per ricavare la sua tensione caratteristica di snervamento fyk sul quale applico il coefficiente di sicurezza dell' acciaio γs per ottenere la tensione di progetto fyd.

La tensione di progetto fyd, insieme con il momento massimo Mmax servono per ricavare il modulo di resistenza a flessione minimo Wxmin.

Questo serve per trovare la sezione della trave che devo poi ingegnerizzare, assicurando che la tensione massima del materiale che ho scelto non supera la tensione di progetto.

 

Dalla tabella dei profilati metallici scelgo l'IPE 360 che soddisfa il mio Wxmin.

 

 

LEGNO

Per il solai di legno ho scelto il modello UNI SOL -12 con i seguenti carichi:

Carico strutturale qs = 0.024 kN/mq

Carico permanente qp = 1.19 kN/mq

Come sempre devo scegliere il mio materiale, riportando la classe di resistenza fmk.

Per il mio solaio scelgo il legno lamellare GL 28h con fmk = 24, che insieme con il coefficiente diminutivo kmod e il coefficiente di sicurezza γm, mi permette di ricavare la mia tensione di progetto 

fd = kmod x fmk / γm

dove kmod: coeff. secondo la durata del carico e la classe di servizio, definito dalla normativa.

        γm: coeff. di sicurezza del mio materiale (=1.45)

Per il dimensione ho bisogno anche della base b della sezione

Wxmin= bh²/6 =Mmax / fmd 

Da questo ricavo hmin verificando sempre che sia superiore della base. Il valore sarà comunque ingegnerizzato.

 

 

 

La struttura che prendo in esame per questa esercitazione è una travatura reticolare spaziale piramidale a base quadrata.

La struttura ipotizzata è soggetta ad un carico concentrato agli spigoli uguale a 100 kN.

Per completare l'esercitazione utilizzo il programma di calcolo strutturale SAP2000 e un foglio Excel.

In seguito sarà spiegato passo per passo il proseguimento:

1) Il primo passo riguarda la modellazione della mia struttura reticolare direttamente nel programma SAP2000. Utilizzo le unità di misura KN, m, C che si può scegliere nel scroll-down menu del programma in alto, facendo NEW MODEL→NEW MODEL INFORMATION→INITIALIZE MODEL WITH DEFAULT UNITS→ KN,m,C.

Vado poi a scegliere l'opzione GRID ONLY sul menu SELECT TEMPLATE.

 

Devo inserire i dati che riguardano i mei NUMBER OF GRID LINES, il numero di campate secondo x,y,z per determinare la mia griglia. Nella selezione GRID SPACING, la lunghezza delle mie aste, inserisco 4m che sarà uguale in tutte le direzioni.

 

Utilizzando il commando FRAME disegno la base della mia trave piramidale controventata alla base quadrata.

 

Seleziono la struttura e facendo Ctrl+C e Ctrl+V formo una struttura 4x6m inserendo sempre le coordinate sugli assi x e y.

 

La modellazione della mia struttura è stata completata.

 

 

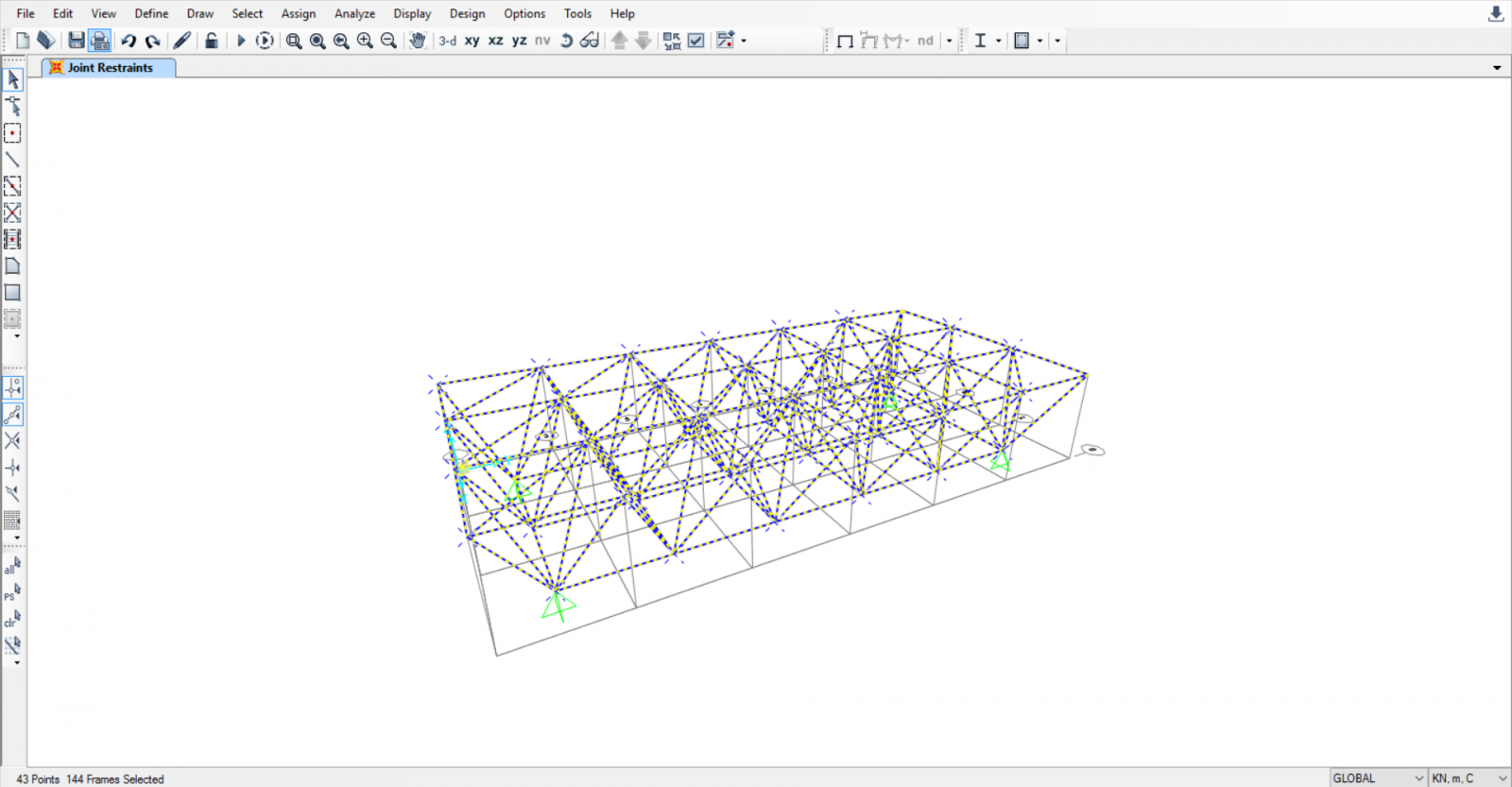
2) Il passo successivo riguarda l'inserimento dei vincoli esterni.

Seleziono i 4 vertici estremi facendo ASSIGN→JOINT→RESTRAINTS e seleziono la ceniera.

 

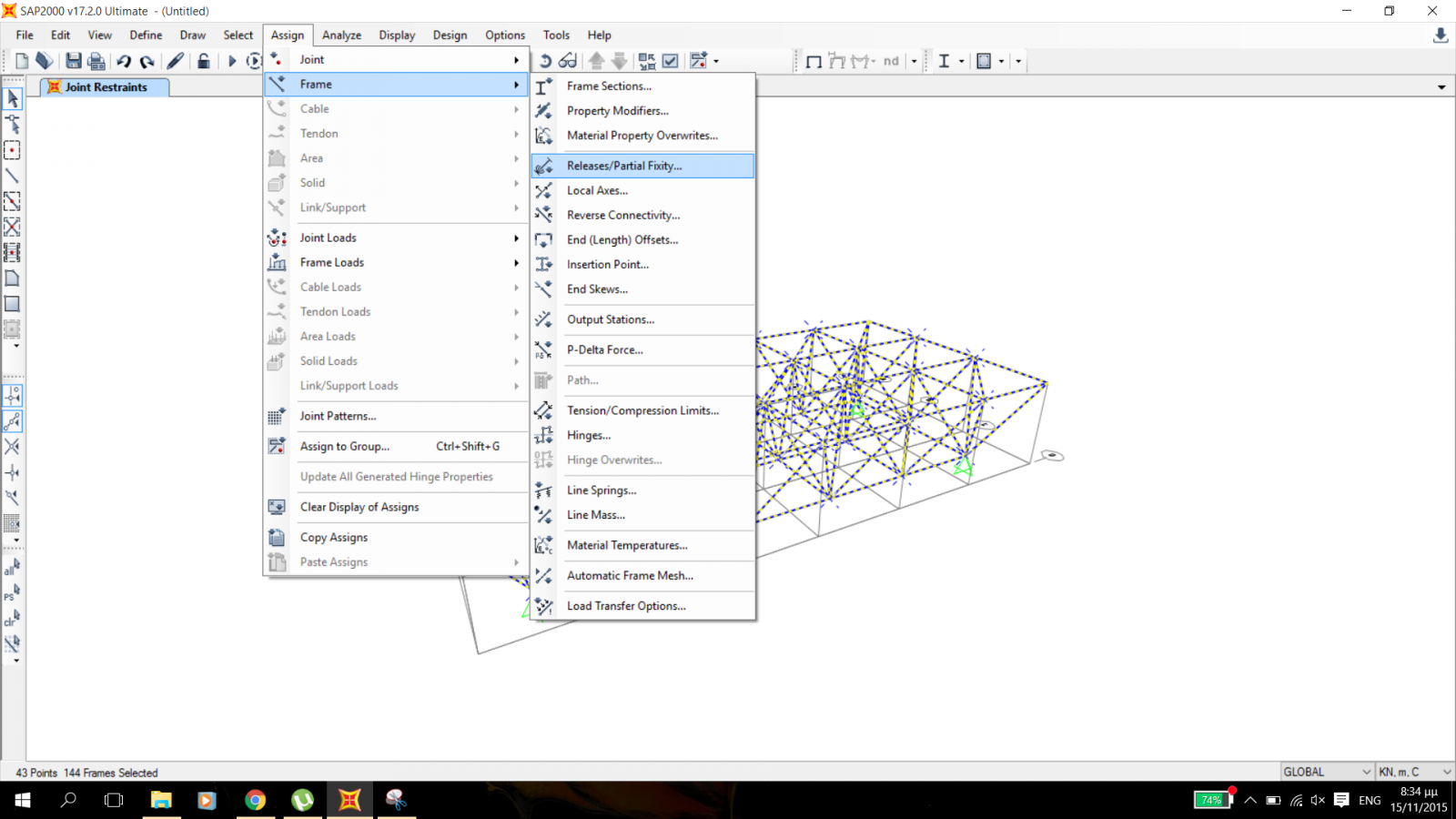
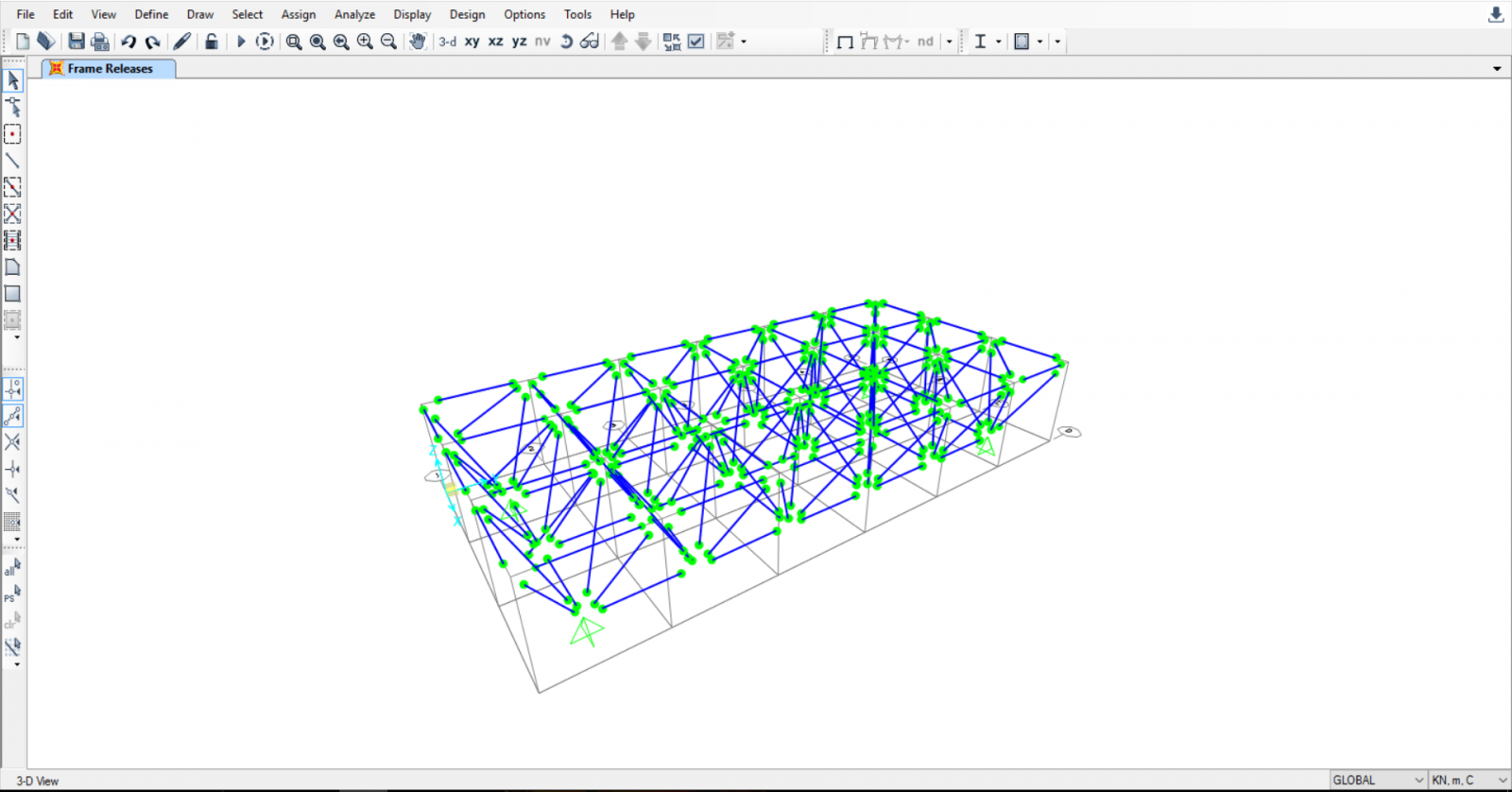
Visto che la mia struttura è una struttura reticolare devo assicurare che i nodi interni sono cerniere interne facendo 

ASSIGN→FRAME→RELEASES/PARTIAL FIXITY e seleziono  Moment 22 e Moment 33, assicurando così che la mia struttura interna sia libera di rotazioni.

 

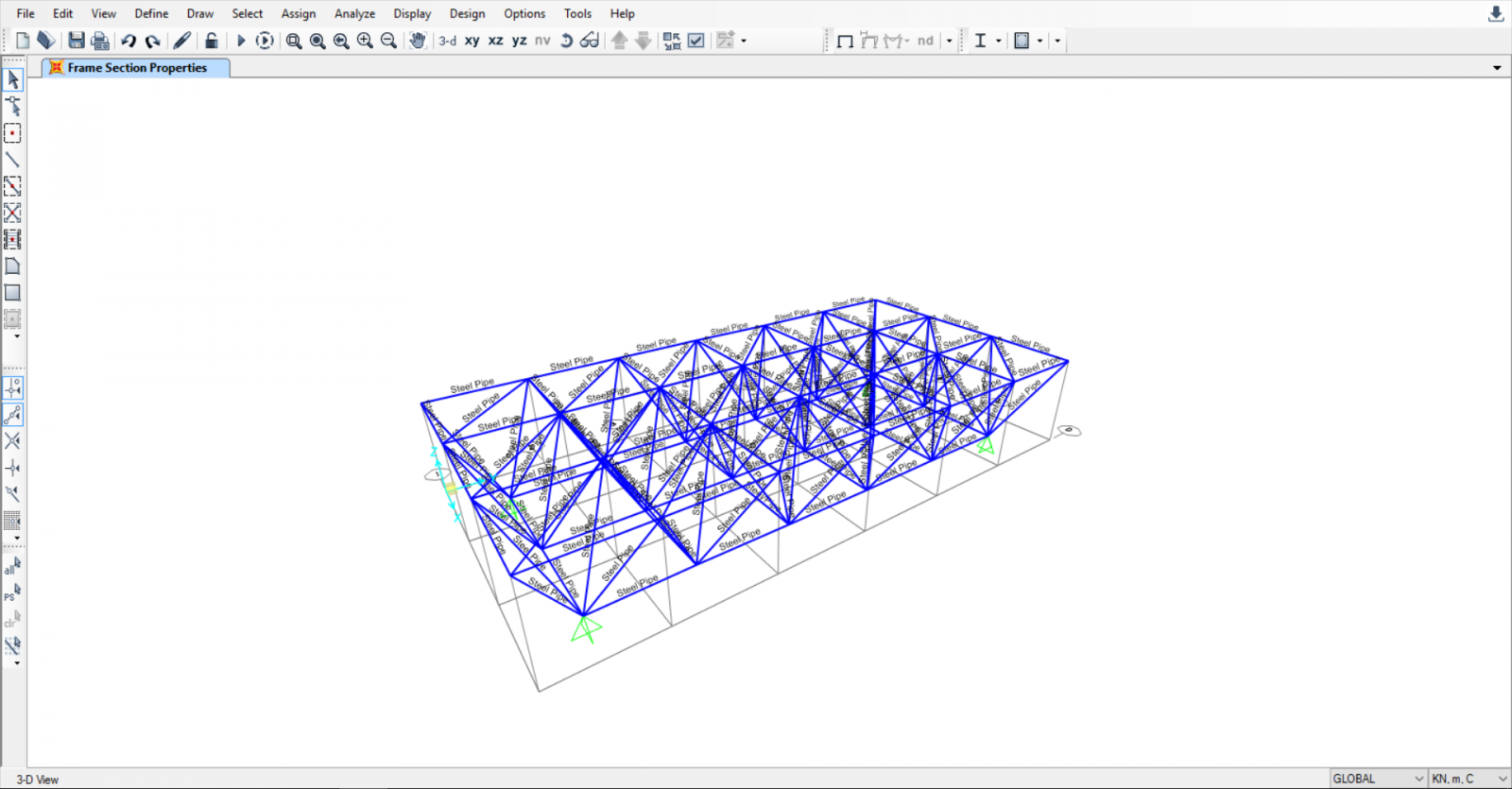
3) Scelgo il materiale della mia sezione facendo 

ASSIGN→FRAME→FRAME SECTION→ADD NEW PROPERTY→FRAME SECTION PROPERTY TYPE→STEEL→ PIPE→OK→OK, inserenedo il nome Steel Pipe per la mia sezione.

 

4) Definisco il carico che assegno alla mia struttura DEFINE→LOAD→LOAD PATTERN→LOAD PATTERN NAME→lo chiamo P→SELF WEIGHT MULTIPLIER inserisco 0 (coefficiente del peso proprio).

 

5) Vado ad assegnare il carico concentrato P sui nodi superiori della struttura.

ASSIGN→JOINT LOADS→FORCES

 

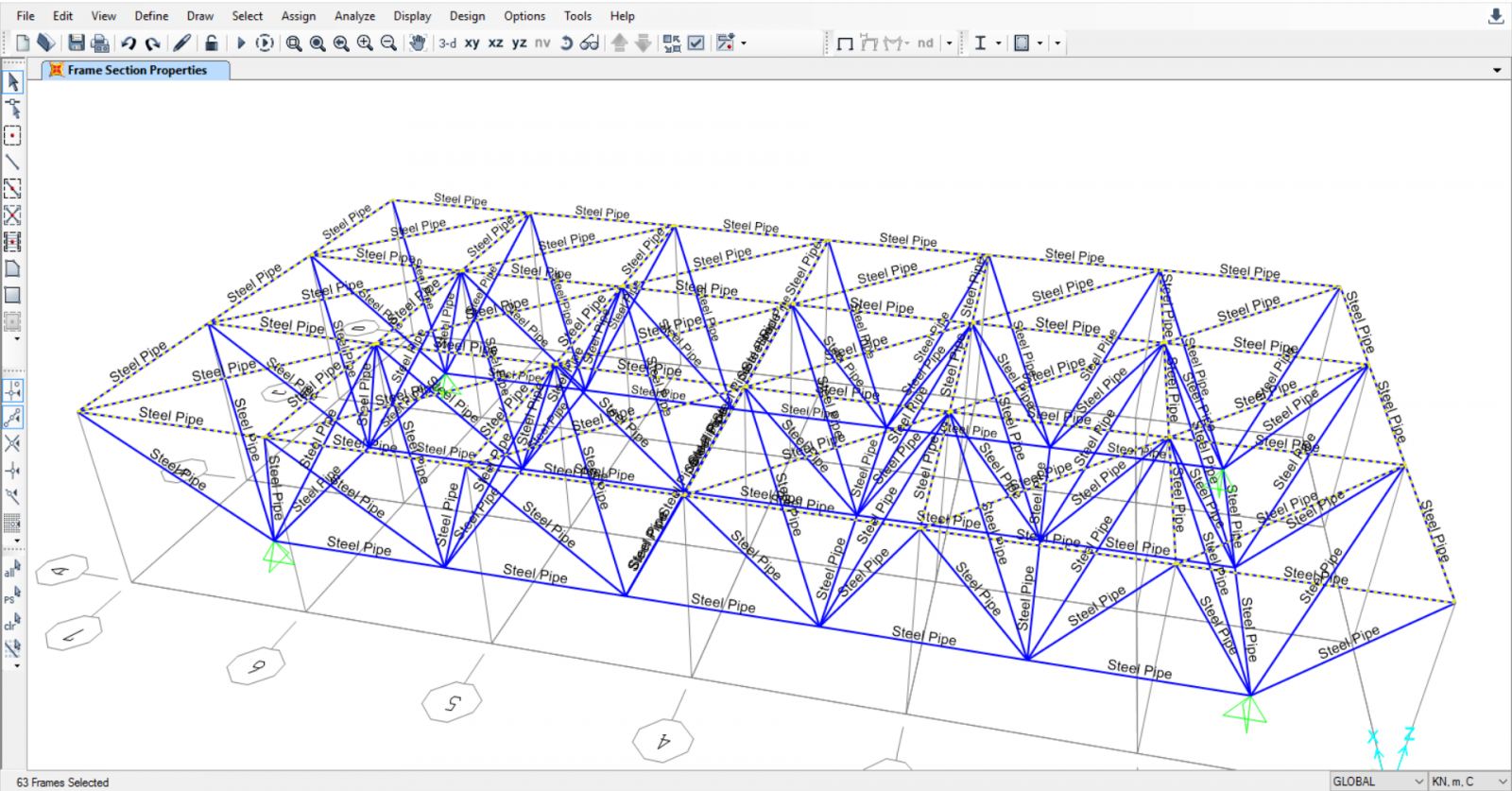
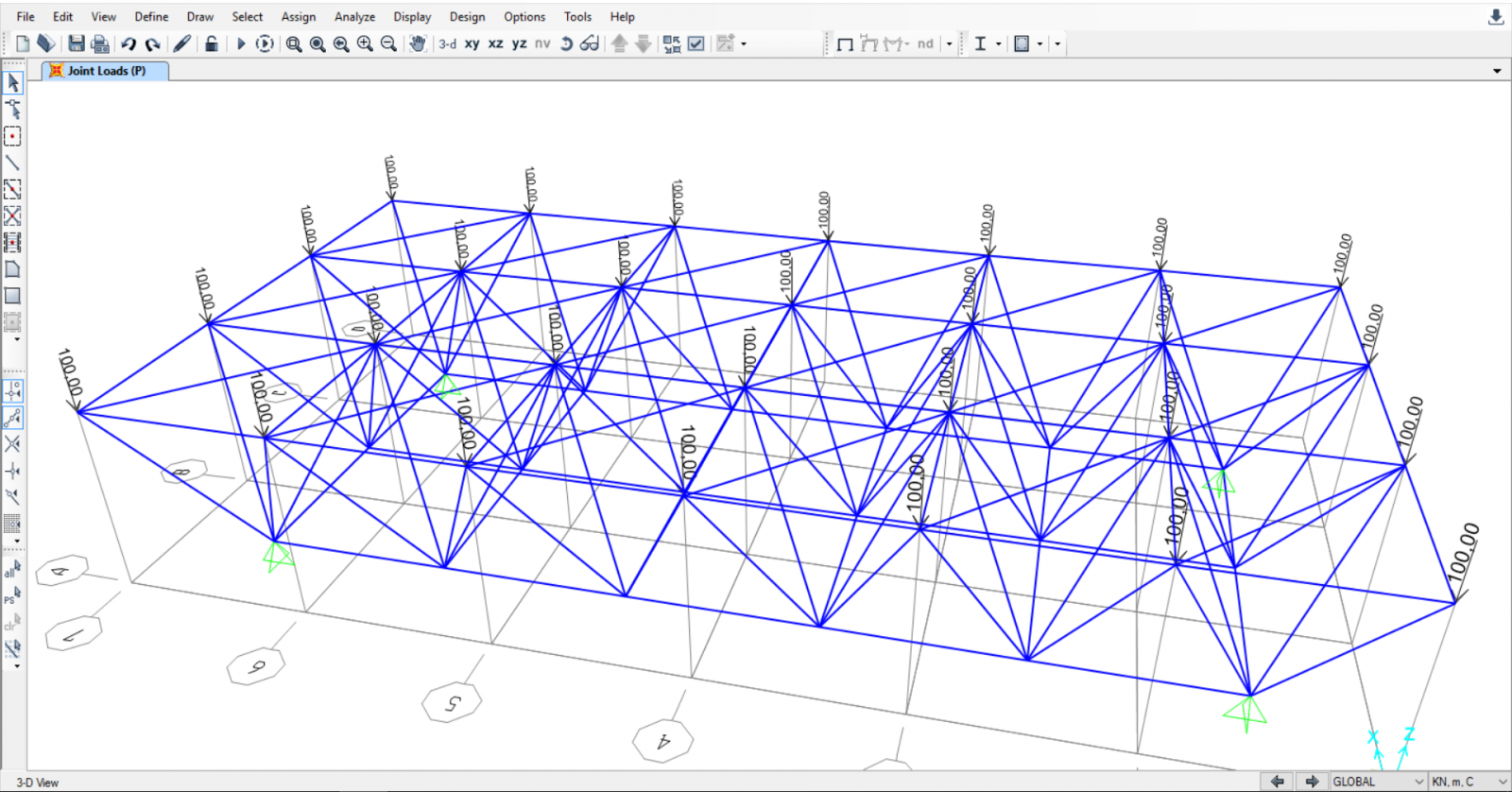
Scelgo il mio carico P, essendo un carico verticale verso il basso (asse z) FORCE GLOBAL Z→ -100 KN

 

Fatto questo è possibile proseguire con l'analisi (il tasto sinistro che si trova sotto il menù scroll down SELECT).

Prendo considerazione solo del mio carico P cliccando DO NOT RUN sul resto.

Clicco RUN NOW

 

La prima informazione che ricavo è la deformata della struttura a causa del carico che ho applicato.

 

Vado pio a verificare che la mia struttura è soggetta solo a SFORZO NORMALE di TRAZIONE se le aste sono TESE o di COMPRESSIONE se sono COMPRESSE. Posso anche sceglire di vedere i valori dei diagrammi.

 

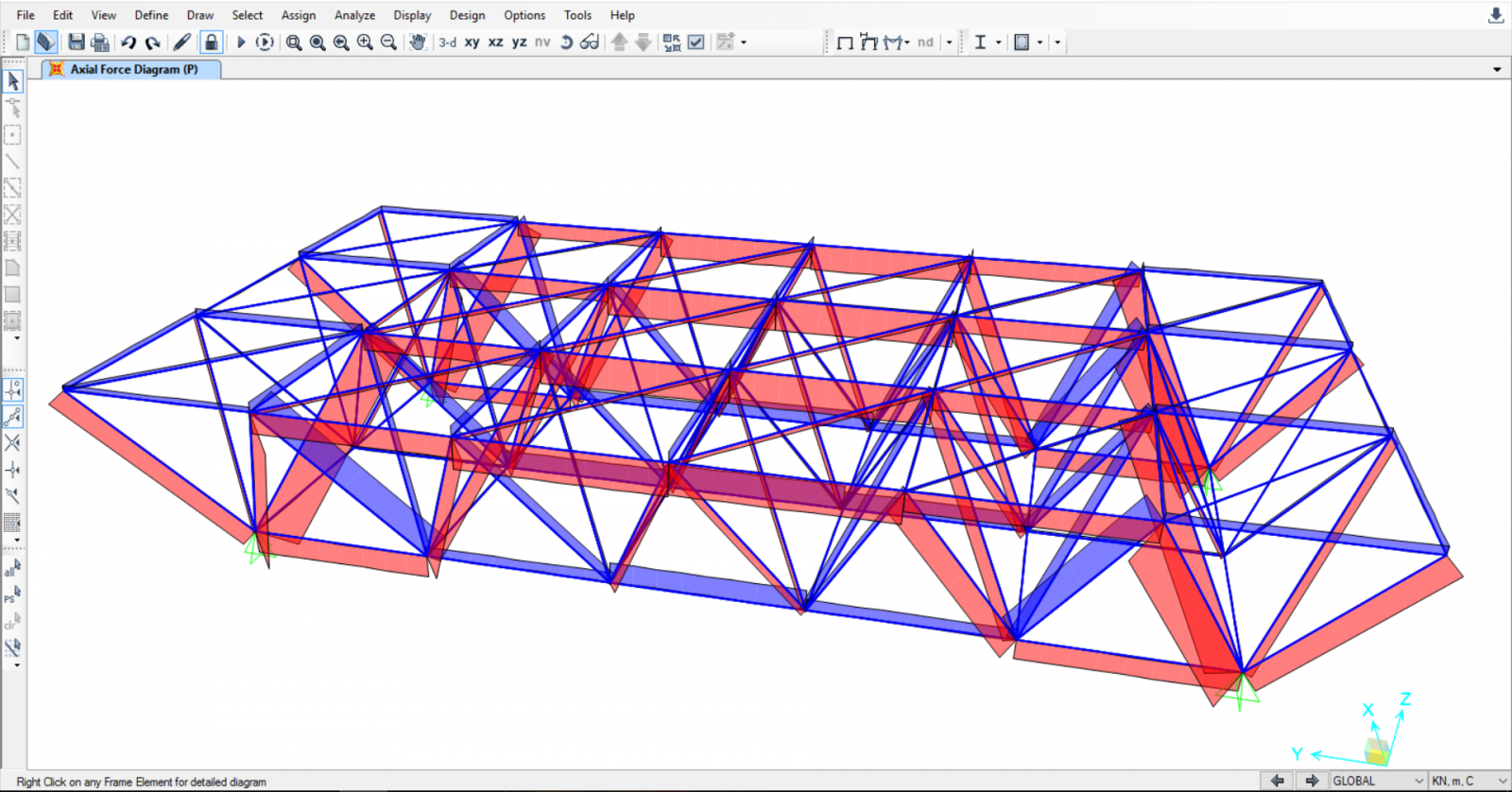
7) Facendo DISPLAY→SHOW (Ctrl+T) vado a prendere tutti i valori di SFORZO NORMALE di ogni asta.

 

Seleziono ANALYSIS RESULTS→ELEMENT FORCES FRAMES

 

Esporto la tabella in Excel

FILE→EXPORT CURRENT TABLE→TO EXCEL

 

8) Dopo l'EXPORT della tabella inserisco in una nuova colonna l le luci delle mia aste e cancello tutto dopo la lettera E nel foglio Excel.

Cancello le parte duplicate facendo DATA→REMOVE DUPLICATES

Ordina la tabella dello SFORZO NORMALE in modo decrescente facendo SORT→FROM HIGHEST TO LOWEST

I valori positivi indicano le aste soggetti a TRAZIONE mentre quelli negativi le aste soggette a COMPRESSIONE

 

 

9) Nel file Excel di TRAZIONE, dopo l'inserimento dello sforzo normale, inserisco anche la resistenza caratteristica dell'acciaio fyk. 

L'acciaio ha lo stesso valore di resistenza sia a trazione che a compressione.

Per la mia struttura ho scelto un acciaio S275.

Poi va inserito il valore del coefficiente di sicurezza dell'acciaio γm, pari a 1.05. Il foglio Excel mi calcola la tensione di progetto fd e l'area minima Amin la ricavo dividendo lo sforzo normale per la tensione di progetto.

Ricavata l'area minima Amin posso ” ingenierizzarla ” per garantire che il materiale resiste allo sforzo maggiore. L'area minima dell'asta maggiormente sollecitata è pari a 7.4 cm2. Vado a cercare nelle tabelle trovando un area di design e trovo il mio profilo. Questa operazione sarà ripetuta per tutte le aste tese della mia struttura.

 

10) Per quanto riguarda la COMPRESSIONE, ordino la tabella FROM HIGHEST TO LOWEST e inserisco le luci di ogni asta.

Il foglio già mi calcola l'area minima ma in più devo inserire il modulo di elasticità E dell'acciaio (210000 MPa) e un coefficiente che dipende dai vincoli esterni delle aste (nel nostro caso, avendo cerniere esterne β =1).

Fatto questo il foglio mi calcola λ, la snellezza della mia asta e Imin, il momento d'inerzia minimo. Questi mi servono per contrastare i due fenomeni di instabilità che sono il  CARICO DI PUNTA e la FLESSO TORSIONE.

Sono tutti parametri che io devo tenere in mente quando faccio la scelta del mio profilo verificando sempre che il mio λ finale sia inferiore di 200.

 

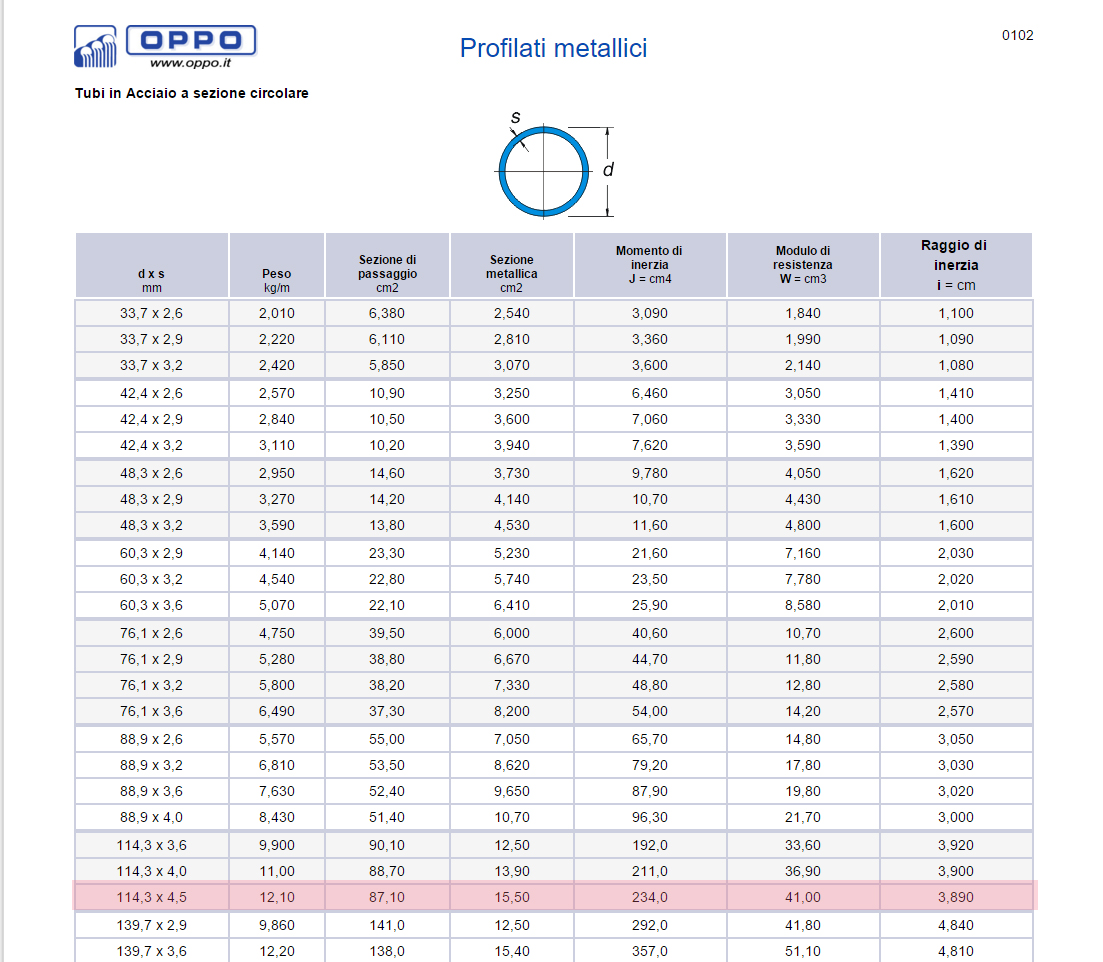
Sia per quelli a TRAZIONE ma anche a COMPRESSIONE cerco di tassonomizzare ed ingegnerizzare i profili e raggruppare in meno profili possibile ma nello stesso tempo verificando che la struttura sia dimensionata in modo corretto.