blog di Valentina.Billardello

 In questa esercitazione bisogna calcolare come viene ripartita una forza orizzontale (sisma o vento), sui diversi telai che compongono la struttura, applicando il metodo delle rigidezze.

Si prende in esame una struttura a telaio in cemento armato e si considera il solaio rigido nel suo piano. Questo è costituito da un insieme di travi e pilastri che permette, oltre a trasmettere carichi verticali alle fondazioni, di sopportare le forze orizzontali svolgendo un ruolo di controventi. Questo sistema di controventi è chiamato telaio SHEAR-TYPE, ovvero, un modello teorico che ha travi infinitamente rigide impedendo che le estremità dei pilastri non ruotino.

Si individuano i telai che compongono la struttura:

Telaio 1v          composto da:        Pilastri 1 e 6

Telaio 2v          composto da:        Pilastri 2, 7 e 11

Telaio 3v          composto da:        Pilastri 3, 8 e 12

Telaio 4v          composto da:        Pilastri 4, 9 e 13

Telaio 5v          composto da:        Pilastri 5 e 10

Telaio 1o          composto da:        Pilastri 1, 2, 3, 4 e 5

Telaio 2o          composto da:        Pilastri 6, 7, 8, 9 e 10

Telaio 3o          composto da:        Pilastri 11, 12 e 13

I controventi vengono schematizzati come molle, aventi un’adeguata rigidezza, poichè rappresentano vincoli cedevoli elasticamente.

STEP 1

Per ottenere la rigidezza traslante degli 8 telai in esame ho bisogno dei seguenti dati:

E = Modulo di Young del cls 21000 MPa

H = altezza dei pilastri 3,50 m

I = momento di inerzia: 266.000 cm⁴ per il pilastro con b 0,50 cm e h 0,40 cm e 416.000 cm⁴ per il pilastro con b 0,40 cm e h 0,50 cm

Applico la seguente formula:

STEP 2

Si riportano nella tabella le rigidezze appena calcolate e le distanze dei  diversi controventi dall’origine 0.

STEP 3

Divido l’impalcato in due figure semplici e trovo il centro di massa e l’area di ognuno di esse.

Si trovano le coordinate del centro di massa tramite la formula:

In realtà questa formula individua il centro d’area dell’impalcato ma poichè la densità dell’impalcato è uniforme il centro d’area e il centro di massa coincidono,  diversamente non utilizzabile.

STEP 4

Possiamo calcolare:

1. Rigidezza totale orizzontale e verticale
2. Coordinate del centro delle rigidezze dell’impalcato
3. Rigidezza torsionale totale

Per la 1 basta sommare tutte le rigidezze traslanti dei controventi orizzontale e poi di quelle verticali.

Per la 2 si utilizza la formula:

e si posiziona così il centro di massa ed il centro delle rigidezze appena trovato all'interno del sistema di riferimento in cui si è disegnato l'impalcato.

Si applicano nel punto G prima una forza orizzontale e poi una verticale.

Se il punto C e il punto G coinciderebbero, l'impalcato soggetto a queste forze (sisma, vento...) traslerebbe nella stessa direzione della forza esterna e non ruoterebbe.

Questi punti non essendo coincidenti tra loro, l'impalcato non solo trasla nella direzione della forza applicata ma subisce una rotazione dovuta dal momento prodotto dalla forza esterna rispetto al centro delle rigidezze.

STEP 5

Definiti i carichi q_s, q_p e q_a agenti sull'impalcato, trovo il carico totale permanente G tramite la formula:

                                                      G = ( q_s +  q_p  ) A_tot

ed il carico totale accidentale Q tramite la formula:

                                                      Q = qa x A_tot

Ora è possibile calcolare il peso sismico W:

                                                      W = G + Ψ_2j x Q 

Ψ_2j = coefficiente di contemporaneità, in questo caso 0,3 categoria B uffici.

Il peso sismico W rappresenta la forza peso dell'edificio, data dal prodotto tra la massa dell'edificio e l'acelerazione di gravità. Poichè il sisma ha un accelerazione mediamente più piccola dell'accelerazione di gravità si introduce un coefficiente di intesità sismica c, che varia a seconda del luogo in cui si progetta il nostro edificio, in questo caso 0,100.

                                                      F = W x c

STEP 6 - 7

Si considera nello STEP 6 una forza sismica che agisce in direzione x provocando una traslazione orizzontale nell'impalcato ed una rotazione rigida.

                                                     u = F / K_{o_tot}

Mentre nello STEP 7 si considera una forza sismica che agisce in direzione y provocando una traslazione verticale nell'impalcato ed una rotazione rigida.

                                                    v = F / K_{v_tot}

rotazione impressa all'impalcato: 

                                                    ϕ = M / K_ϕ

Possiamo ora ricavare la forza sui singoli controventi quando la forza è parallela all'asse x utilizzando le formule :

Possiamo ora ricavare la forza sui singoli controventi quando la forza è parallela all'asse y utilizzando le formule :

L'obiettivo dell'esercitazione è analizzare la deformabilità di una trave a sbalzo maggiormente sollecitata attraverso l'utilizzo di tre tecnologie costruttive differenti: ACCIAO - LEGNO - CLS.

Si prende in esame una pianta destinata ad uso residenziale e tramite l'orditura del solaio si trova:

• Area di Influenza    = 20 mq
• Luce                        = 4 m
• Interasse                 = 5 m

Per prima cosa bisogna trovare le stesse informazioni come nell'esercitazione 2, ovvero, calcolare il dimensionamento della trave. In questo caso però il momento flettente massimo, M_max,  sarà calcolato non più con l'equazione di una trave doppiamente appoggiata ma con l'equazione di una mensola ad incastro:

                                                      M_max = (q_u l²)/2                            

Dopo aver dimensionato la sezione si deve effettuare la verifica a deformabilità controllando l'abbasamento massimo della trave in rapporto alla sua luce. Questo si effettua allo Stato Limite di Esercizio SLE, stato subito dopo il quale la struttura non si rompe, ma a causa di spostamenti e deformazioni cambia nella sua conformazione limitando la possibilità d’utilizzo dell’edificio. 

Si calcolano perciò nuovamente i carichi incidenti sulla struttura moltiplicando il coefficiente di combinazione ψ al q_a :

                                                    q_e = (q_{s +} q_{p +} q_a x ψ) x i 

Nel caso dell'acciaio e del cemento armato si tiene conto del peso propro della trave, dunque si moltiplica al q_e, mentre nel caso del legno no pechè è un materiale leggero e quindi viene trascurato il valore del peso proprio.

Si trova il modulo elastico E ed il momento di Inerzia I_x per poter calcolare successivamente l'abbassamento massimo ν_max :

                                                     ν_max = (q_e l⁴)/8EI_x   

Si può così verificare se il rapporto tra la luce della trave e il suo abbassamento massimo sia maggiore a 250, come imposto dalla normativa. 

Si riprende la stessa tecnologia del solaio studiati nell'esercitazione 2:

SBALZO TRAVE ACCIAIO

q_P =  0,19 + 0,6 + 0,03 + 1,0 + 0,5 =  2,32 KN/m²

• pavimentazione in gres porcellanato: 0,19 KN/m²
• massetto di tipo tradizionale: 0,03 m x 20 KN/m³ = 0,6 KN/m²
• isolamento acustico ACUSTIC SYSTEM 7: 0,03 KN/m²
• tramezzi: 1,0 KN/m²
• impianti: 0,5 KN/m²

q_s = 2,44  + 0,188 = 2,628 KN/m²

• lamiera grecata mod. E/S 4000 e getto di calcestruzzo h 12 cm :  2,44 KN/m²
• travetto IPE 180 :  0,188 KN/m > 0,188 (KN/m)  / 1 (m_interasse) = 0,188 KN/m²

^​q_a =  2 KN/m²   ambienti ad uso residenziale

Calcolo il q_u e trovo M_{max .} 

Scelgo la classe di resistenza dell'acciaio f_yk = 275 MPa e trovo  f_yd e W_xmin .

Il valore W_xmin è 1511,45 cm³, dunque trovo sulla tabella dei profilati IPE il valore successivamente maggiore a quest'ultimo per definire il W_x di design, che è uguale a 1930,0 cm³ IPE 500.

Si aggiunge il peso della trave al q_s:

q_s = 2,44  + 0,188 + 0,181 = 2,8 KN/m²

• lamiera grecata mod. E/S 4000 e getto di calcestruzzo h 12 cm :  2,44 KN/m²
• travetto IPE 180 :  0,188 KN/m > 0,188 (KN/m)  / 1 (m_interasse) = 0,188 KN/m²
• trave IPE 300 :  0,907 KN/m > 0,907 (KN/m)  / 5 (m_interasse) = 0,181 KN/m²

​Calcolo ora il q_e  e nonostante il carico sia stato modificato, il rapporto tra la luce di libera inflessione e l'abbassamento massimo è maggiore di 250.

l/νmax=412,846 > 250  

Il dimensionamento risulta corretto.

SBALZO TRAVE LEGNO

q_P =  0,216 + 0,6 + 0,03 + 1,0 + 0,5 + 0,9 =  3,306 KN/m²

• pavimentazione in parquet di rovere:  0,03 m x 7,2 KN/m³  = 0,216 KN/m²
• massetto di tipo tradizionale: 0,03 m x 20 KN/m³ = 0,6 KN/m²
• isolamento acustico ACUSTIC SYSTEM 7: 0,03 KN/m²
• caldana: 0,04 m x 24 KN/m³ = 0,96 KN/m²
• tramezzi: 1,0 KN/m²
• impianti: 0,5 KN/m²

^​q_s =  0,21 + 0,036 =  0,246  KN/m²

• assito:  0,21 KN/m²
• travetti :  1m x 0,20m x 0,30m x 0,6 KN/m³ = 0,036 KN/m²

 q_a =  2 KN/m²   ambienti ad uso residenziale

Calcolo il q_u e trovo M_{max .} 

Scelgo il legno lammellare GL24h con f_mk = 24 con k_mod= 0,60 e γ_m= 1,45.

Posso calcolare la tensione di progetto f_d = 9,93

Imposto una base di 40 cm trovando così un h_min = 70,72 cm e la ingegnerizzo portandola a un H = 75 cm. Ottengo una trave 40x70cm.

In questo caso, come già detto, il legno è un materiale leggero e quindi il peso proprio della trave viene trascurato.

Calcolo il q_e = 23 KN/m e il rapporto tra la luce l e l'abbassamento risulta  > 250.

l/vmax= 617,86 >250.

Il dimensionamento risulta corretto.

SBALZO TRAVE C.A.

q_P =  0,19 + 0,6 + 0,03 + 0,13 + 1,0 + 0,5 =  2,45 KN/m²

• pavimentazione in gres porcellanato: 0,19 KN/m²
• massetto di tipo tradizionale: 0,03 m x 20 KN/m³ = 0,6 KN/m²
• isolamento acustico ACUSTIC SYSTEM 7: 0,03 KN/m²
• intonaco: 0,13 KN/m²
• tramezzi: 1,0 KN/m²
• impianti: 0,5 KN/m²

q_s = 3,19  +  0,053 = 3,243 KN/m²

• pignatta 20x40x25 + caldana 5 cm :  3,19 KN/m²
• rete elettrosaldata (maglia 15cmx15cm  ø8): 5,3 Kg/m² = 0,053 KN/m²

^​q_a =  2 KN/m²   ambienti ad uso residenziale

Calcolo il q_u e trovo M_{max .} 

Per l'acciaio scelgo la classe B450C che ha una resistenza di snervamento f_yk = 450 MPa e trovo: f_yd = 391,30 N/mm²

Per trovare invece la tensione di progetto del calcestruzzo scelgo come classe di resistenza f_ck (C 40/50) e trovo: f_cd = 17 N/mm²

Si trova  h_u, impostando una base di 45 cm, si aggiunge il valore δ per trovare H_min =62,65 cm. 

Questo valore si ingegnerizza portandolo alla decina superiore dunque : H = 70 cm.

Calcolo il q_e = 41,34 KN/m e il rapporto tra la luce l e l'abbassamento risulta  > 250.

l/vmax= 816,74 >250.

Il dimensionamento risulta corretto.

L'obiettivo dell'esercitazione è dimensionare la trave più sollecitata attraverso l'utilizzo di tre tecnologie costruttive differenti: ACCIAO - LEGNO - CLS.

Si prende in esame una pianta destinata ad uso residenziale e tramite l'orditura del solaio si trova:

• Area di Influenza    = 30 mq
• Luce                        = 6 m
• Interasse                = 5 m

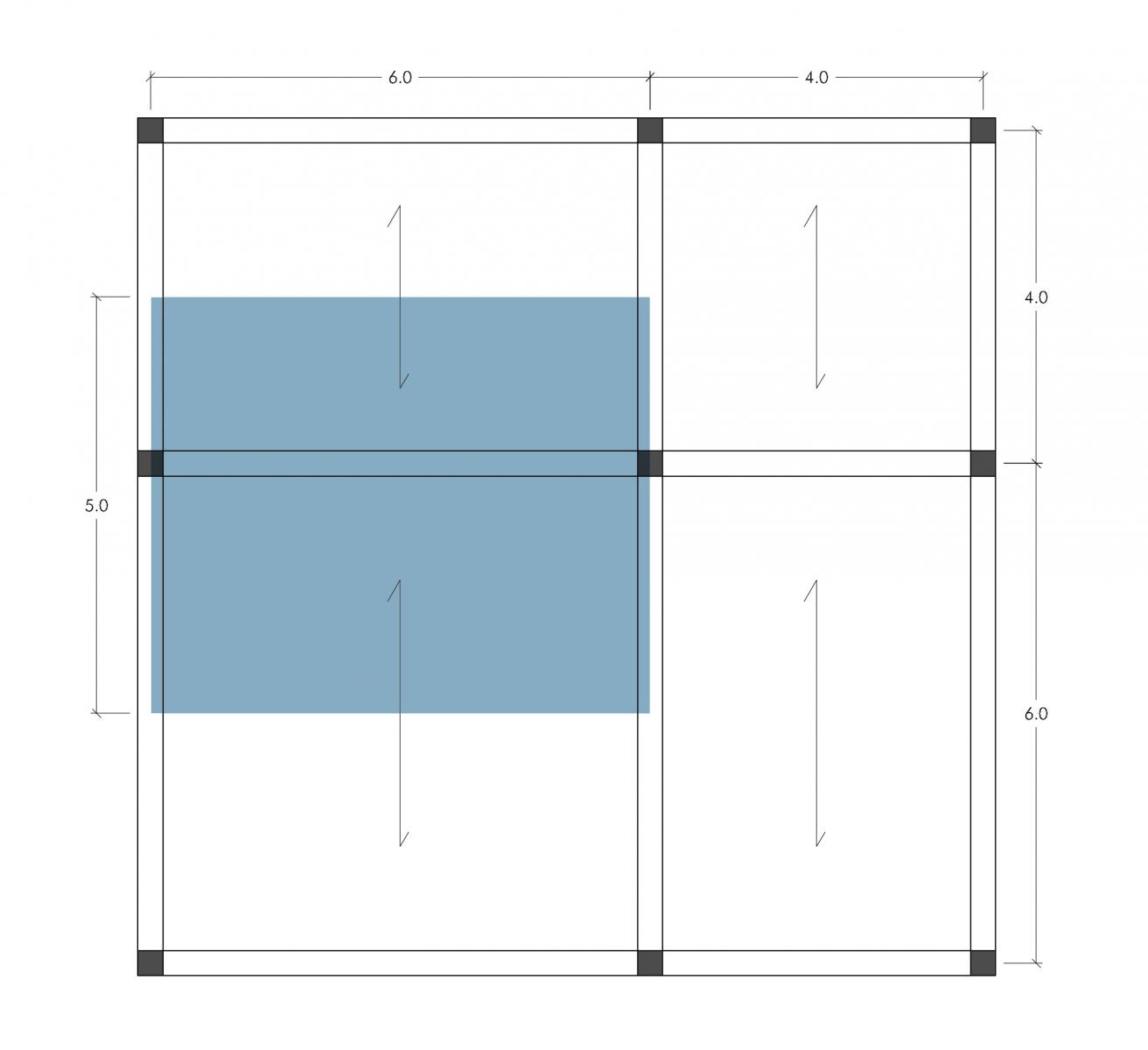
Per prima cosa bisogna determinare tutti i carichi agenti sulle tre tipologie di solaio, prendendo in analisi 1m² di solaio, rappresentato in sezione:

• q_s_carico strutturale: è il carico dovuto al peso proprio di tutti gli elementi strutturali.
• q_p_carico permanente: è il carico dovuto al peso proprio di tutti gli elementi che gravano sulla struttura del solaio e non hanno funzione portante. 
• q_a_carico accidentale: è il carico definito dalla normativa NTC20008-Norme tecniche per le costruzioni-D. M. 14 Gennaio 2008 e definisce i carichi d'esercizio che l'edificio svolge.

Per ricavare il q_tot non si può solamente sommare i diversi carichi trovati ma bisogna moltiplicarli con dei coefficienti moltiplicativi come vuole la normativa:

                                    q_tot = 1,3xq_s + 1,5xq_p + 1,5xq_a = KN/m²

Per ricavare il carico agente sulla trave in esame bisogna moltiplicare il qtot con l'interasse, così facendo si ricava q_u.

                                     q_u = q_tot x i =  KN/m

Si determina il momento massimo che agisce sulla trave, ed essendo la nostra trave doppiamente appoggiata già sappiamo il valore di M_{max= (}q_u l²)/8. 

Adesso ricavo tutti i valori elencati per ogni differente tecnologia utilizzata in modo da poter dimensionare correttamente la sezione della trave.

Dimensionamento trave in ACCIAIO:

Per prima cosa trovo la dimensione dei travetti con interasse=1m e luce=5m

q_P =  0,19 + 0,6 + 0,03 + 1,0 + 0,5 =  2,32 KN/m²

• pavimentazione in gres porcellanato: 0,19 KN/m²
• massetto di tipo tradizionale: 0,03 m x 20 KN/m³ = 0,6 KN/m²
• isolamento acustico ACUSTIC SYSTEM 7: 0,03 KN/m²
• tramezzi: 1,0 KN/m²
• impianti: 0,5 KN/m²

q_s = 2,44  KN/m²

• lamiera grecata mod. E/S 4000 e getto di calcestruzzo h 12 cm : 2,44 KN/m²

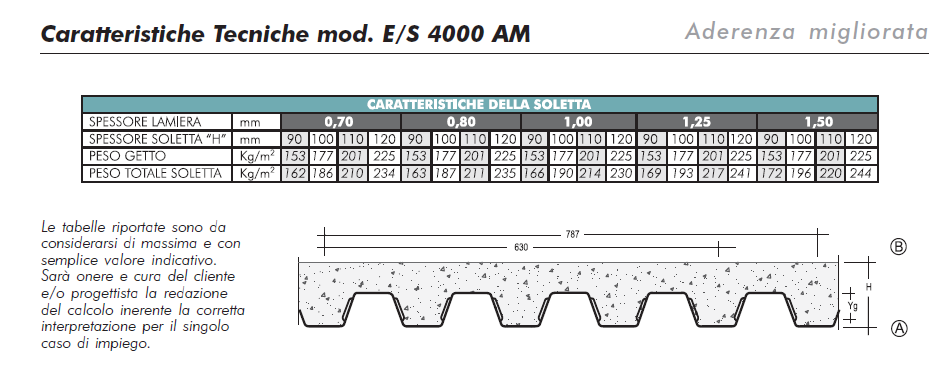
q_a =  2 KN/m²   ambienti ad uso residenziale

Calcolato il q_u, moltiplicato per l’interasse_, e il M_max   scelgo il tipo di acciaio con cui andrò a progettare i travetti.

Il valore che distingue un acciaio dall’altro è la tensione caratteristica di snervamento, f_yk, che individua la classe di resistenza del materiale.

                                                       f_yk = 275 MPa.

Questo valore dovrò dividerlo con il coefficiente parziale di sicurezza γ_s= 1,05 per ottenere la tensione di progetto f_yd.

                                                                 f_{yd =} f_yk / γ_s

Adesso posso dimensionare il travetto perchè i dati richiesti per trovare il modulo di resistenza a flessione minimo sono f_yd e M_max.

                                                      W_xmin = M_max / f_yd

W_xmin è il valore minimo che la sezione deve avere affinchè nessuna fibra del materiale superi la tensione dl progetto. Questo valore viene ingegnerizzato andando ad aggiungere il peso proprio nei successivi calcoli e scelto un valore del modulo di resistenza a flessione superiore a  W_xmin , compatibile con i profili esistenti sul mercato (profilati IPE).

                            W_xmin =115,17 cm³              W_x di progetto è IPE 180

Calcolo con il peso proprio dei travetti:

q_s = 2,44  + 0,188 = 2,628 KN/m²

• lamiera grecata mod. E/S 4000 e getto di calcestruzzo h 12 cm :  2,44 KN/m²
• travetto IPE 180 :  0,188 KN/m > 0,188 (KN/m)  / 1 (m_interasse) = 0,188 KN/m²

Ottengo W_xmin =118,08 cm³    e quindi il dimensionamento risulta corretto.

Adesso effettuo gli stessi calcoli per andare a trovare la sezione della TRAVE con interasse=5m e luce=6m.

                            W_xmin =850,41 cm³              W_x di progetto è IPE 360

Calcolo con il peso proprio della trave:

q_s = 2,44  + 0,188 +0,1142 = 2,742 KN/m²

• lamiera grecata mod. E/S 4000 e getto di calcestruzzo h 12 cm :  2,44 KN/m²
• travetto IPE 180 : 0,188 KN/m²
• travetto IPE 180 :  0,571 KN/m > 0,571 (KN/m) / 5 (m_interasse) = 0,1142 KN/m²

Ottengo W_xmin =823,06 cm³    e quindi il dimensionamento risulta corretto.

Dimensionamento trave in LEGNO:

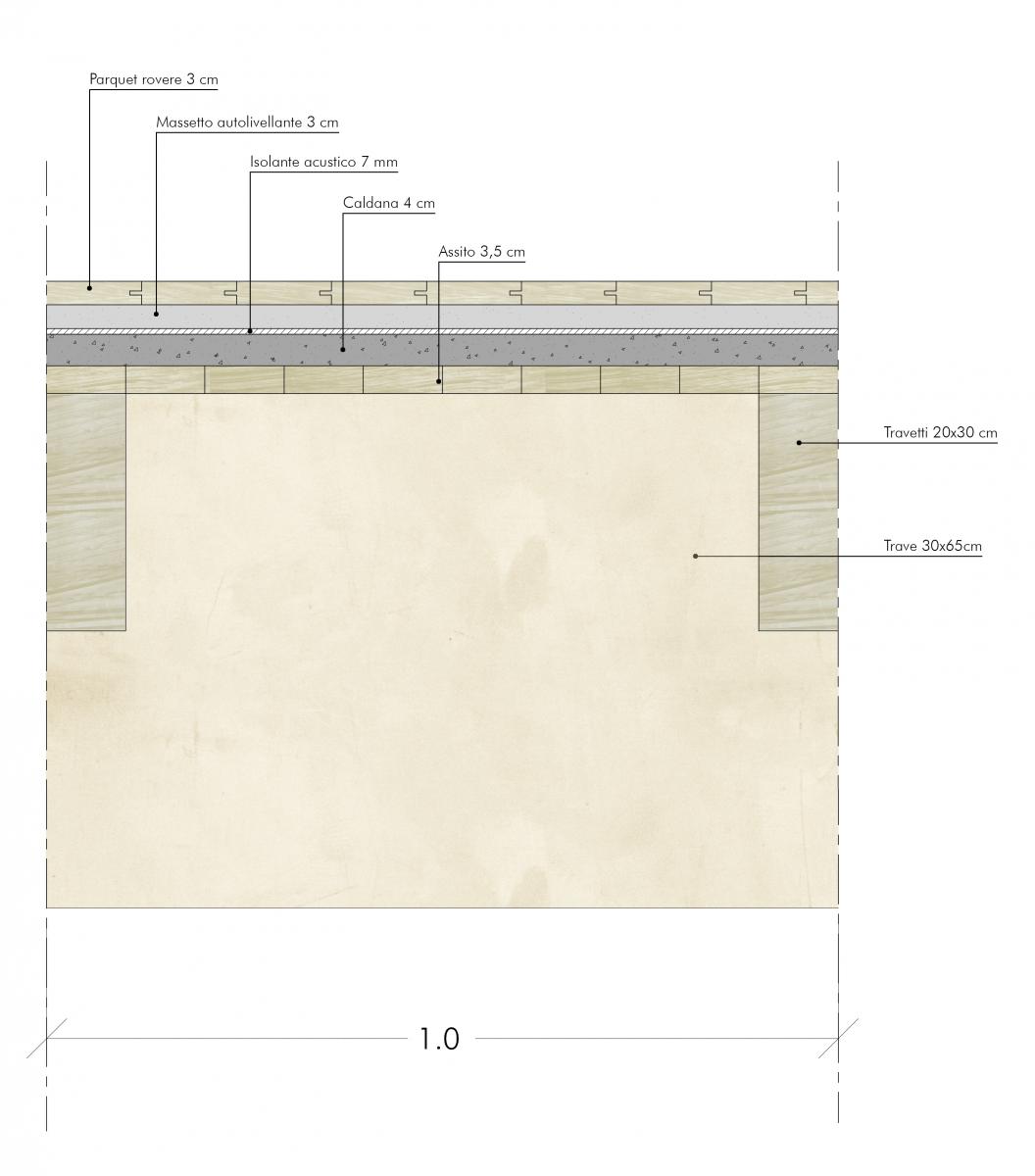
Per prima cosa trovo la dimensione dei travetti con interasse=1m e luce=5m:

q_P =  0,216 + 0,6 + 0,03 + 1,0 + 0,5 + 0,9 =  3,306 KN/m²

• pavimentazione in parquet di rovere:  0,03 m x 7,2 KN/m³  = 0,216 KN/m²
• massetto di tipo tradizionale: 0,03 m x 20 KN/m³ = 0,6 KN/m²
• isolamento acustico ACUSTIC SYSTEM 7: 0,03 KN/m²
• caldana: 0,04 m x 24 KN/m³ = 0,96 KN/m²
• tramezzi: 1,0 KN/m²
• impianti: 0,5 KN/m²

q_s =   0,21  KN/m²

• assito:  0,21 KN/m²

^​q_a =  2 KN/m²   ambienti ad uso residenziale

Calcolato il q_u , moltiplicato per l'interasse, e il M_max   scelgo la tecnologia del legno, in questo caso lamellare, in modo da ricavare la resistenza a flessione f_mk guardando la normativa.

Si sceglie il legno lammellare GL24h con f_mk = 24.

Il k_mod  è un coefficiente diminuitivo dei valori di resistenza del materiale che tiene conto l’effetto della durata del carico e delle condizioni di umidità dove la struttura viene esercitata. Questo si ricava dalla normativa scegliendo la durata del carico (Permanente più di 10 anni) e la classe di servizio ( classe di servizio 1, appartengono a tale classe gli elementi lignei protetti contro le intemperie come quelli posti all’esterno degli edifici in ambienti condizionali). Trovo k_mod= 0,60.

γ_m è il coeficiente parziale di sicurezza relativo al materiale e lo ritroviamo in questa tabella.

Prendo  γ_m= 1,45.

Trovati questi valori posso calcolare la tensione di progetto f_d, attraverso la formula:

                                                   f_d=  (k_modxf_mk)/γ_m

Posso ricavare la sezione rettangolare dei travetti sapendo che nel legno i dati necessari per calcolare l’altezza sono b, M_max e f_d.

                                                  h_min = (M_max/b)^^0.5 x (6/ f_d)^^0.5

Approssimando le dimensioni  trovate ottengo un travetto di dimensioni 20x30cm.

Effettuo nuovamente i calcoli con il foglio elettronico aggiungendo il carico dei travetti al carico strutturale per verificare il risultato precedentemente ottenuto:

q_s =  0,21 + 0,036 =  0,246  KN/m²

• travetti :  1 x 0,20m x 0,30m x 0,6 KN/m³ = 0,036 KN/m²

Ottengo un’altezza pari al dimensionamento precedentemente ipotizzato, risulta corretto. 

Adesso effettuo gli stessi calcoli per andare a trovare la sezione della TRAVE con interasse=5m e luce=6m.

Trovo la trave ingegnerizzata 30x65 cm. Ricalcolo aggiungendo il peso proprio al q_s , quindi si calcola il nuovo momento e così si verifica la resistenza della trave. 

Il peso specifico del legno lamellare classe GL 24 h è 3,80 kN/ mc

q_s =  0,21 + 0,036 + 0,74 =  0,986   KN/m²

• trave: 0,3 m x 0,65 m x 3,80 KN/m³ =   0,74 KN/m² 

 Il dimensionamento risulta corretto.

Dimensionamento trave in CLS:

1. Costruisco una travatura reticolare spaziale su SAP costituita da piramidi rovesciate, controvettate, di dimensioni 2x2x2 sviluppata su una maglia ortogonale con modulo 8x6 .

2. Aggiungo  tramite l'operazione Define > Section Properties > Frame Section una nuova sezione, in questo caso Tubolare Cava (PIPE), rinominandola "asta", poichè questa sarà la sezione scelta per tutta la travatura reticolare.

3. Tramite il comando Assign > Frame > Frame Section assegno su tutta la struttura la sezione "asta" appena creata.

4.  Per trasformare i nodi delle aste in cerniere, bisogna effettuare il rilascio dei momenti tramite il comando Assign > Frame > Release/Partial fixity > Release, si spunta su Moment 22 e Moment 33 e nello start e nell’end inserisco i valori 0, rendendo libera la rotazione all’inizio e alla fine di ogni asta.

5. Inserisco le cerniere in modo casuale lungo il piano x,y, (aiutandomi con la vista 2d tramite View > Set View 2d (piano x,y  z=0) ) utilizzando il comando Assign > Joint > Restrain.

6. Assegno delle forze concentrate nei nodi strutturali. Creo prima la forza F : Define > Load Pattern  inserendo dove è scritto DEAD la lettera F e il valore 0 al posto di 1, clicco su Add New Load Pattern.

7. Seleziono la parte interna superiore della struttura, aiutandomi sempre con Set View 2d, ed eseguo il comando: Assign > Joint Loads > Forces assegnando la forza F precedente creata inserendo il valore -100 su Force Global Z. Successivamente seleziono il perimetro superiore della struttura inserendo una forza dimezzata di -50, poichè l'area di influenza dei nodi laterali perimetrali sono la metà dei nodi interni alla struttura. 

8. Inserite tutte le forze necessarie per l’Avvio dell’Analisi vado sul tasto Play (triangolo sulla toolbar) e seleziono prima DEAD e Modal dove imposto RUN/DO NOT RUN CASE, e dopodichè seleziono la forza F e clicco su Run NOW.

9. Adesso, per vedere cosa è successo alla mia struttura clicco prima su Show Deformed Shape (sempre sulla toolbar) e vedo la deformazione, poi su Show forces > Frame/Cables.. e vedo gli sforzi assiali lungo le aste reticolari.

10. Per visualizzare le tabelle con tutti i valori della struttura vado su : Display > Show Tables > Analysis Result. Spunto la casella Analysis Result. Vado su Select Load Pattern e seleziono la forza F. La tabella che a noi servirà sarà: Element Forces-Frames perchè fornisce il numero delle aste e le loro caratteristiche di sollecitazione a sforzo Normale.

11. Essendo questa struttura composta da aste di 3 lunghezza differente, creo 3 tabelle Excel differenti, ognuna la quale ha le sue rispettive misure in modo tale da sapere quale sforzo normale agisce su di essa. Per fare ciò vado su Select > Select > Select Lines Parallel To > Click Straight Line Objet e seleziono le aste con la stessa misura: per esempio, incomincio con le aste che misurano tutte 2 (aste dei rettangoli), poi 2,4495 (le diagonali delle piramidi) e infine 2,8284 (le diagonali dei rettangoli).

12.  Eseguo le stese operazioni per le tre diverse tabelle Excel ricavate dalla struttura :

1. Ordino i valori di Station, eliminando i valori diversi da 0.
2. Cancello i valori dopo la casella P (sforzo Normale).
3. Scrivo il dato L, lunghezza dell’asta in esame.

​​

13. Scaricata la tabella Excel fornita da questo sito, copio i dati che vanno dalla casella L in poi su un nuovo foglio Excel. Unifico i dati forniti da SAP e i dati della tabella scaricata. Ordino i valori di P (sforzo normale) dal più piccolo al più grande, in modo da avere aste compresse (valore negativo-blu) separate dalle aste in trazione (valore positivo-rosso). Sul dato N inserisco i valori del dato P tutti col segno positivo, per farlo inserisco la funzione: =E3*(-1) e la riporto fino a dove i valori di P sono negativi.

14. DATI:

      fyk  rappresenta la classe dell'Acciaio  scelta S235 e quindi il valore è 235 MPa per tutte le aste.

      γ_m  è il coefficiente di sicurezza e vale 1,05.

      β   è il coefficiente di vincolo e vale 1 perchè l'asta è vincolata da due                                      cerniere.

      E   è il modulo di elasticità dell'acciaio e vale 210000MPa.

      l   è la lunghezza delle aste e quindi avendole già riportate scrivo la                                       funzione =F3.

15. FORMULE: queste formule vanno scritte nel linguaggio Excel sotto i dati richiesti.

     f_yd = f_yk / γ_m          resistenza allo snervamento del materiale di progetto

     A_min= N / f_yd​          Area minima della sezione

     I_min= A_min x ρ²_min      momento di Inerzia minmo

      ρ_min= l₀ / λ*         raggio di Inerzia minimo

     λ*= π (E/f_yd)^1/2         coefficiente di snellezza massimo

     I_min, ρ_min,  λ*        questi valori sono importanti da calcolare nelle aste soggette a compressione ma                           no in quelle a trazione

16. SEZIONE: 

Per trovare le sezioni delle aste, vado sul sito http://www.oppo.it/tabelle/profilati-tubi-circ.htm  e trovo i valori di A_design, I_design  e  ρ_min  che li troviamo scritti sulla tabella OPPO su Sezione metallica, Momento di Inerzia e Modulo di Resistenza. Il Profilo corrisponde a dxs.

L'Area di design deve essere superiore all'Area minima e uguale per Inerzia di design che deve essere superiore all'Inerzia minima.

IMPORTANTE: il valore della snellezza λ non deve superare il valore 200.