blog di Ilaria.Mattioli

In questa terza esercitazione dimensioneremo una mensola verificando che il valore del rapporto tra la luce e l’abbassamento v_max sia maggiore di 250.

La mensola in questione ha luce di 3 m e interasse di 6 m. La sua area di influenza (segnata in verde) è di 18 mq.

Per poter dimensionare la mensola abbiamo bisogno di determinare i carichi gravanti su di essa, che si distinguono in carichi strutturali (qs), carichi permanenti non strutturali (qp) e infine carichi accidentali (qa). Questi carichi sono già stati calcolati per la precedente esercitazione.

Altro dato determinante ai fini del dimensionamento è il valore del momento massimo M_max. Trattandosi di una mensola il momento massimo sarà pari a ql²/2. 

ACCIAIO

TOTALE CARICHI STRUTTURALI qs = q1 + q2  = 2,492 KN/m²

TOTALE CARICHI PERMANENTI qp:  q1 + q2+ q3 + q4 + q5 = 2,9 KN/m²

TOTALE CARICHI ACCIDENTALI qa: Carico secondo normativa: 2 KN/m²

Combinazione allo SLU per 1mq di solaio: q = 2,492 (1,3) + 2,9 (1,5) + 2 (1,5) = 10,6 KN/m²
Carico totale agente sulla trave: qtot = q x A = 10,6 KN/m² x 18 m² = 190,8 KN
Carico lineare agente sulla trave: qu = q x i= 10,6 x 6m = 63,6 KN/m
Momento massimo della trave: Mmax = (qu x l²)/2 = (63,6 x 3²)/2 = 286 KNm

Tensione caratteristica di snervamento (acciaio S275): f_yk =235 MPa
Tensione caratteristica di progetto: f_yd = 223,81 MPa
Modulo di resistenza a flessione (minimo): W_x,min = 1277,5 cm³

DAL SAGOMARIO SCELGO IPE 450 => Wx,min = 1500 cm3  

Inserisco nella tabella Excel il valore del momento di inerzia Ix = 33740 cm4

Posso verificare che la sezione scelta rispetti i limiti di abbassamento, calcolando il Qe con cui è possibile calcolare l’abbassamento massimo della trave vmax e verificare che il rapporto tra luce e abbassamento sia maggiore di 250 (come da normativa). 

CALCESTRUZZO ARMATO

TOTALE CARICHI STRUTTURALI qs = q1 + q2 + q3 = 3,42 KN/m²

TOTALE CARICHI PERMANENTI qp:  q1 + q2+ q3 + q4 + q5 + q6 + q7 = 4,38 KN/m²

TOTALE CARICHI ACCIDENTALI qa: Carico secondo normativa: 2 KN/m²

Combinazione allo SLU per 1mq di solaio: q = 3,42 (1,3) + 4,38 (1,5) + 2 (1,5) = 14 KN/m²
Carico totale agente sulla trave: qtot = q x A = 14 KN/m² x 18 m² = 252 KN
Carico lineare agente sulla trave: qu = q x i= 14 x 6m = 84 KN/m
Momento massimo della trave: Mmax = (qu x l²)/2 = (84 x 3²)/2 = 378 KNm

Resistenza caratteristica dell’acciaio: f_yk= 450 MPa  
Resistenza caratteristica del cls: f_ck = 30 Mpa
Resistenza di progetto dell’acciaio: f_yd = f_yk / 1,15 = 391,30 Mpa
Resistenza di progetto del cls: f_cd = 0,83 x (f_ck/ 1,15) = 17 Mpa

Valore della base della trave (ipotizzato): b = 40 cm
Altezza utile della trave: hu = r (Mmax x 100 / f_cd x b))0,5 = 56,99 cm
Altezza minima della trave: hmin = hu + δ = 61,99 cm  dove δ è uguale alla distanza tra il baricentro dell’armatura ed il filo del cls teso
Valore di H scelto: H = 65 cm

A questo punto posso ottenere il peso unitario della trave e il Qe e verifico che:
l/v_max > 250
In questo caso è pari a 960 quindi la sezione è verificata

LEGNO

TOTALE CARICHI STRUTTURALI qs = q1 + q2 = 0,84 KN/m²

TOTALE CARICHI PERMANENTI qp:  q1 + q2+ q3 = 2 KN/m2

TOTALE CARICHI ACCIDENTALI qa: Carico secondo normativa: 2 KN/m2

Combinazione allo SLU per 1mq di solaio: q = 0,84 (1,3) + 2 (1,5) + 2 (1,5) = 7,092 KN/m²
Carico totale agente sulla trave: qtot = q x A = 7,092 KN/m² x 18 m² = 127,65 KN
Carico lineare agente sulla trave: qu = q x i= 7,092 x 6m = 42,55 KN/m
Momento massimo della trave: Mmax = (qu x l²)/2 = (42,55 x 3²)/2 = 191,5 KNm

Resistenza a flessione caratteristica: f_m,k = 24 MPa (dipende dal tipo di legno) 
Coefficiente di durata del carico: k_mod= 0,6 
Coefficiente parziale di sicurezza del materiale: γm= 1,50 
Tensione ammissibile: f_d = f_m,k x k_mod / γm = 9,60 MPa

Valore della base della trave (ipotizzato): b = 35 cm
Altezza minima della trave: hmin = (interasse x Mmax x 1000 / (b x f_d)^0,5 = 54,70  cm
Valore di H scelto: H = 60 cm
 

Devo calcolare l’abbassamento della trave v_max, in quanto il rapporto tra luce ed abbassamento deve essere, per normativa, maggiore di 250

l/v_max > 250

In questo caso è di 740,24 quindi la sezione è verificata

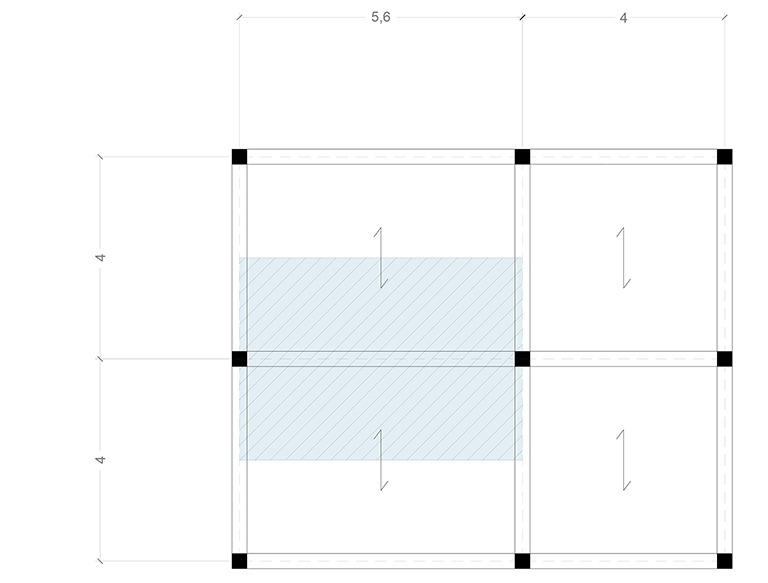
Questa seconda esercitazione prevede l’individuazione, in una pianta di carpenteria, della trave maggiormente sollecitata e il suo conseguente dimensionamento (in base al materiale impiegato).

In questo caso la trave maggiormente sollecitata ha luce di 5,6 m e interasse di 4 m. La sua area di influenza (segnata in celeste) è di 22,4 mq.

Per poter dimensionare la trave abbiamo bisogno di determinare i carichi gravanti su di essa, che si distinguono in carichi strutturali (qs), carichi permanenti non strutturali (qp) e infine carichi accidentali (qa).

Altro dato determinante ai fini del dimensionamento è il valore del momento massimo M_max. Trattandosi di una trave appoggiata il momento massimo si troverà in corrispondenza della mezzeria e sarà pari a ql²/8. 

ACCIAIO

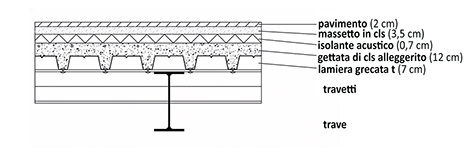
Carichi strutturali (qs)
-Lamiera grecata tipo HI BOND A55/P600:   
                                  s = 0,07 m
                                  q1 =0,092 KN/m²

Gettata di cls alleggerito: γ = 20,00 KN/m³
                                     stot = 0,12 m
                                     q2 = 2,4 KN/m²

TOTALE CARICHI STRUTTURALI qs = q1 + q2  = 2,492 KN/m²

Carichi permanenti (qp)
- Pavimento: γ = 20,00 KN/m³
                    s = 0,02 m
                    q1 = 20 x 0,02 = 0,4 KN/m²

- Massetto in cls:  γ = 20,00 KN/m³
                           s = 0,035 m
                           q2 = 20 x 0,035 = 0,7 KN/m²

- Isolante acustico Fonoroll pb: γ = 10 KN/m³
                                              s = 0,03 m
                                              q3 = 0,3 KN/m²

- Incidenza impianti: q4 = 0,5 KN/m²

- Incidenza tramezzi: q5 = 1 KN/m²

TOTALE CARICHI PERMANENTI qp:  q1 + q2+ q3 + q4 + q5 = 2,9 KN/m²

Carichi accidentali (qa)
Carico secondo normativa: 2 KN/m²

Combinazione allo SLU per 1mq di solaio: q = 2,492 (1,3) + 2,9 (1,5) + 2 (1,5) = 10,6 KN/m²
Carico totale agente sulla trave: qtot = q x A = 10,6 KN/m² x 22,4 m² = 237,44 KN
Carico lineare agente sulla trave: qu = q x i= 10,6 x 4m = 42,4 KN/m
Momento massimo della trave: M_max = (qu x l²)/8 = (42,4 x 5,6²)/8 = 166 KNm

Tensione caratteristica di snervamento (acciaio S275): f_yk =275 MPa
Tensione caratteristica di progetto: f_yd = 261,90 MPa
Modulo di resistenza a flessione (minimo): W_x,min = 633,99 cm³

DAL SAGOMARIO SCELGO IPE 330 => W_x,min = 713 cm³  

Per la verifica si aggiunge il peso proprio della sezione ai carichi strutturali, si ricalcola M_max e si ridetermina W_x,min che dovrà essere minore di 713 cm³

p.p. IPE = 0,49 KN/m
q = 2,982 (1,3) + 2,9 (1,5) + 2 (1,5) = 11,22 KN/m²
qtot = q x A = 11,22 KN/m² x 22,4 m² = 251,3 KN
qu = q x i= 11,22 x 4m = 44,9 KN/m
Mmax = (qu x l²)/8 = (44,9 x 5,6²)/8 = 176 KNm
Wx,min = 672,13 cm³      VERIFICATO

LEGNO

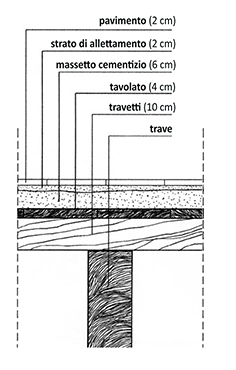
Carichi strutturali (qs)
-Tavolato in legno (abete):   γ = 6,00 KN/m³
                                         s = 0,04 m
                                         q1 = 6 x 0,04 = 0,24 KN/m²

- Travetti: γ = 6,00 KN/m³
               s = 0,1 m
               q2 = 6 x 0,1 = 0,6 KN/m²

TOTALE CARICHI STRUTTURALI qs = q1 + q2 = 0,84 KN/m²

Carichi permanenti (qp)
- Pavimento: γ = 20,00 KN/m³
                    s = 0,02 m
                    q1 = 20 x 0,02 = 0,4 KN/m²
- Strato di allettamento:  γ = 20,00 KN/m³
                                    s = 0,02 m
                                    q2 = 20 x 0,02 = 0,4 KN/m²
- Massetto: γ = 20,00 KN/m³
                  s = 0,06 m
                  q3 = 20 x 0,06 = 1,2 KN/m2

TOTALE CARICHI PERMANENTI qp:  q1 + q2+ q3 = 2 KN/m²

Carichi accidentali (qa)
Carico secondo normativa: 2 KN/m²

Combinazione allo SLU per 1mq di solaio: q = 0,84 (1,3) + 2 (1,5) + 2 (1,5) = 7,092 KN/m²
Carico totale agente sulla trave: qtot = q x A = 7,092 KN/m² x 22,4 m² = 158,86 KN
Carico lineare agente sulla trave: qu = q x i= 7,092 x 4m = 28,37KN/m
Momento massimo della trave: Mmax = (qu x l²)/8 = (28,37 x 5,6²)/8 = 111,20 KNm

Resistenza a flessione caratteristica: fm,k = 24 MPa (dipende dal tipo di legno) 
Coefficiente di durata del carico: kmod= 0,8 (normativa - NTC 2008) 
Coefficiente parziale di sicurezza del materiale: γm= 1,45 (caratteristica del legno lamellare)
Tensione ammissibile: fd = fm,k x kmod / γm = 13,24 MPa

Valore della base della trave (ipotizzato): b = 35 cm
Altezza minima della trave: hmin = (interasse x Mmax x 1000 / (b x fd)^0,5 = 37,94  cm
Valore di H scelto: H = 50 cm
  

CALCESTRUZZO ARMATO

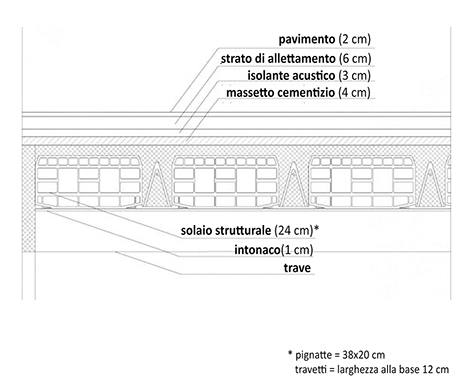
Carichi strutturali (qs)
-Soletta in cls:   γ = 25,00 KN/m³
                        s = 0,04 m
                        q1 = 25 x 0,04 = 1 KN/m²

- Travetti: γ = 25,00 KN/m³
               smedio = 0,12 x 0,2 / 0,5 =  0,048 m
               q2 = 25 x 0,048 = 1,2 KN/m²

- Pignatte: γ = 8,00 KN/m³
                smedio = 0,38 x 0,2 / 0,5 = 0,152 m 
                q3 = 8 x 0,152 = 1,22  KN/m²

TOTALE CARICHI STRUTTURALI qs = q1 + q2 + q3 = 3,42 KN/m²

Carichi permanenti (qp)
- Pavimento: γ = 20,00 KN/m³
                    s = 0,02 m
                    q1 = 20 x 0,02 = 0,4 KN/m²

- Strato di allettamento:  γ = 20,00 KN/m³
                                    s = 0,06 m
                                    q2 = 20 x 0,06 = 1,2 KN/m²

- Isolante acustico Fonoroll pb: γ = 10 KN/m³
                                              s = 0,03 m
                                              q3 = 0,3 KN/m²

- Massetto: γ = 20,00 KN/m³
                  s = 0,04 m
                  q4 = 20 x 0,04 = 0,8 KN/m²

- Intonaco: γ = 18,00 KN/m³
                 s = 0,01 m
                 q5 = 18 x 0,01 = 0,18 KN/m²

- Incidenza impianti: q6 = 0,5 KN/m²

- Incidenza tramezzi: q7 = 1 KN/m²

TOTALE CARICHI PERMANENTI qp:  q1 + q2+ q3 + q4 + q5 + q6 + q7 = 4,38 KN/m²

Carichi accidentali (qa)
Carico secondo normativa: 2 KN/m²

Combinazione allo SLU per 1mq di solaio: q = 3,42 (1,3) + 4,38 (1,5) + 2 (1,5) = 14 KN/m²
Carico totale agente sulla trave: qtot = q x A = 14 KN/m² x 22,4 m² = 313,6 KN
Carico lineare agente sulla trave: qu = q x i= 14 x 4m = 56 KN/m
Momento massimo della trave: Mmax = (qu x l²)/8 = (56 x 5,6²)/8 = 219,77 KNm

Resistenza caratteristica dell’acciaio: fyk= 450 MPa  
Resistenza caratteristica del cls: fck = 45 Mpa
Resistenza di progetto dell’acciaio: fyd = fyk / 1,15 = 391,30 Mpa
Resistenza di progetto del cls: fcd = 0,83 x (fck/ 1,15) = 25,50 Mpa

Valore della base della trave (ipotizzato): b = 30 cm
Altezza utile della trave: hu = r (Mmax x 100 / fcd x b))^0,5 = 37,30 cm
Altezza minima della trave: hmin = hu + δ = 42,30 cm  dove δ è uguale alla distanza tra il baricentro dell’armatura ed il filo del cls teso

Valore di H scelto: H = 50 cm

Con il software Sap 2000 possiamo modellare una travatura reticolare spaziale e ottenere dati necessari al dimensionamento, che verrà effettuato con l’ausilio dei fogli di calcolo di Excel.

1 – Dalla schermata iniziale clicchiamo sul File -> New model -> Grid Only (solo dopo essersi accertati che le unità di misura siano impostate su KN,m,C) e successivamente impostiamo la geometria della griglia.

2 – Si apre la schermata in pianta e in 3D. Con il comando Draw Frame/Cable disegniamo il modulo

3 – Quando il modulo è stato completato, selezioniamo gli elementi da copiare e con i comandi Ctrl+C -> Ctrl+V  si apre la schermata su cui impostare le coordinate dell’elemento che si va ad aggiungere a quello copiato. Una volta raggiunto  il numero di moduli desiderati lungo l’asse Y copiamo gli stessi in direzione X, selezionandoli e con Ctrl+C -> Ctrl+V  inseriamo il valore per l’asse X nella schermata delle coordinate.

4 – A questo punto la struttura è completata 

5 -  Selezioniamo tutto e assegniamo una sezione alla struttura cliccando su Assign -> Frame -> Frame section. Scegliamo il tipo di materiale e il tipo di sezione da assegnare

6 – Per i rilasci selezioniamo tutto e clicchiamo su Assign -> Frame -> Releases/Partial Fixity. Spuntiamo moment 22 minor (start-End) e moment 33 major (start-End). Sulla struttura vengono visualizzati i rilasci.

7 – Per assegnare i vincoli clicchiamo su View -> Set 2D view e impostiamo Z=0. Selezioniamo i nodi in corrispondenza dei quali posizionare i vincoli. Andiamo su Assign -> Joints -> Restraints, clicchiamo sull’icona della cerniera e diamo Ok. Nella vista 3D sono visibili i vincoli appena assegnati.

8 -  Per assegnare i carichi, ci posizioniamo in pianta a quota 2 e selezioniamo con una finestra da sinistra verso destra i nodi centrali. Clicchiamo su Assign -> Joint Loads -> Forces e clicchiamo sul + accanto al menu a tendina DEAD per aggiungere un nuovo carico. Aggiungiamo il nuovo carico che chiameremo F. Assegniamo il valore del carico su Force Global Z (con il meno perché rivolto verso il basso).

9 – Sulla vista 3D è possibile verificare l’effettiva assegnazione del carico. Per i carichi sui nodi perimetrali proseguiamo con lo stesso procedimento ma assegniamo al carico un valore dimezzato (perché l’area di influenza è la metà). Ora posso visualizzare sulla struttura tutti i carichi assegnati.

10 – A questo punto abbiamo tutti gli elementi per avviare l’analisi, quindi clicchiamo sull’icona Play (Run Analysis) in alto a sinistra e quindi Run Now (per i carichi DEAD e Modal scegliere l’opzione Do Not Run). E’ ora possibile visualizzare la deformata della struttura e i diagrammi delle sollecitazioni. Trattandosi di una struttura reticolare, le aste dovranno essere soggette solo a sforzo normale.

11 -  Per visualizzare le tabelle di calcolo da esportare su Excel è sufficiente digitare Ctrl+T e spuntare Analysis Results, cliccare su Select Load Patterns e quindi selezionare F e dare OK.

12 – Dalla tabella apriamo il menù a tendina in alto a destra e selezioniamo Element Forces – Frames e esportiamo su Excel. Da questa tabella eliminiamo tutti i dati che non ci servono o che sono ripetuti. Evidenziamo in rosso i dati delle aste compresse, lasciando in nero i dati delle aste tese e procediamo al dimensionamento. 

13 - Per prima cosa dimensioniamo le aste tese, avvalendoci del foglio di calcolo Excel per il dimensionamento dei pilastri, nel quale andiamo ad inserire i valori dello sforzo normale di trazione per ciascuna asta.

Inseriamo il tipo di acciaio che vogliamo impiegare (in questo caso S235) e i relativi valori f_yk, il coefficiente di sicurezza γ_m (pari a 1,05) e il conseguente f_yd, cioè la tensione di progetto (che viene calcolata in automatico nella tabella excel in quanto rapporto tra la resistenza caratteristica f_yk e il coefficiente di sicurezza). Possiamo quindi trovare l’area minima di ogni asta.

A questo punto abbiamo i valori delle aree minime per le aste tese, che posso raggruppare per poter scegliere almeno due tipi di profilati in modo tale da evitare un sovradimensionamento. 

14 – Per le aste compresse oltre ad f_yk, γ_m, e f_yd devo tener conto anche del momento di inerzia I_x e del raggio giratore di inerzia ρ_x

Come prima, inseriamo i valori dello sforzo normale (in questo caso il modulo in quanto i valori sono negativi trattandosi di compressione), il β (in questo caso equivalente ad 1 perché si tratta di aste incernierate) e la lunghezza espressa in metri di ciascuna asta. In base ai valori di Area Minima, Momento d’Inerzia minimo e raggio giratore di inerzia minimo scegliamo il profilato adatto da un sagomario e inseriamo i valori corrispondenti.  

Fatto ciò controllo che il valore della snellezza λ non sia superiore a 200.