Esercitazione 1
Un accenno sulle Travature Reticolari
Le travature reticolari sono strutture composte da un insieme di aste appartenenti allo stesso piano che generano un forma in grado di coprire ampie luci. La generica travatura reticolare è caratterizzata da correnti superiori e correnti inferiori, montanti e diagonali. Inoltre la struttura reticolare prevede nel suo sistema un insieme di cerniere, “nodi”, che sono gli unici punti che ricevono le forze e le ridistribuiscono sulle aste attraverso le azioni di contatto, in questo caso solo attraverso gli sforzi assiali N perché sono gli unici ad agire su questo tipo di strutture. Altra peculiarità è che le aste possono essere tese o compresse a seconda del tipo di forze che agiscono sulla struttura o scariche se queste hanno solamente la funzione di completamento geometrico della struttura.
Travatura reticolare simmetrica
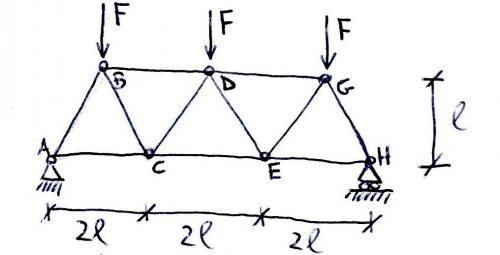
Questo tipo di travatura reticolare presenta un struttura regolare con dei carichi concentrati nei nodi e la sua geometria presenta una simmetria rispetto all’asse centrale, quello passante per il nodo D. Per questo motivo, prima di eseguire l’esercizio, si deduce che al fine di calcolare le azioni di contatto sulla trave, sarà necessario sezionare solamente metà struttura perché questa è simmetrica.
Prima di procedere con il calcolo delle reazioni vincolari, verifico che la struttura sia isostatica attraverso la formula: V = L (gradi di vincolo = gradi di libertà)
I gradi di vincolo a loro volta sono: V = Ve + Vi (Gradi di vincolo = vincoli esterni + vincoli interni)
I vincoli esterni sono 3, 2 per la cerniera (traslazione orizzontale e verticale) e 1 per il carrello (traslazione verticale); quelli interni invece si calcolano con la formula: 2 (n-1)(n numero di aste che la cerniera collega).
Nodi A-H: 2 (2-1)= 2 x 2= 4
Nodi B-G: 2 (3-1)= 4 x 2= 8
Nodi C-D-E: 2 (4-1)= 6 x 3= 18; quindi i gradi di vincolo interni sono: 30 Vi + 3 Ve = V.
Essendo V = L (struttura isostatica); allora L = 33.
Un’ altra formula ancora più rapida per verificare l’isostaticità è: Ve + a = 2n(vincoli esterni + numero di aste = 2 numero dei nodi). In questo caso abbiamo 3+11=2 (7). .jpg)
A questo punto possiamo calcolare le reazioni vincolari attraverso gli equilibri alle traslazioni orizzontale e verticale. Da questi otteniamo che Ru1= 0 perché non deve equilibrare alcuna forza orizzontale; mentre le reazioni Rv1 e Rv2 equilibrano le tre forze concentrate F quindi saranno pari a: Rv1=Rv2=3/2F.
Ottenuti i valori delle reazioni vincolari si può procedere al calcolo delle azioni di contatto sulla travatura reticolare attraverso due metodi:
1)METODO DELLE SEZIONI DI RITTER
2) METODO DEI NODI
1)con questo metodo si opera una sezione che tagli 3 aste NON CONVERGENTI SULLO STESSO NODO e si determinano le azioni di contatto su ogni asta attraverso gli equilibri alle traslazioni verticali e orizzontali, e l’equilibrio dei momenti rispetto ad un polo scelto;
2)con questo metodo invece si isolano i nodi della struttura e si calcolano le azioni di contatto solo attraverso gli equilibri alle traslazioni verticali e orizzontali.
In entrambi i casi le azioni di contatto, di compressione o di trazione, sono raffigurate con semplici frecce la cui punta può essere uscente dall’asta/nodo o entrante nell’asta/nodo; la differenza tra i due metodi è che nel primo, quello delle sezioni, la freccia uscente dall’asta indica per convenzione la trazione quindi uno sforzo positivo, nel caso opposto indica compressione quindi sforzo negativo; nel metodo dei nodi il ragionamento è lo stesso in quanto le frecce uscenti dai nodi indicano la trazione e quelle entranti la compressione. .jpg)
Scegliendo il metodo delle sezioni di Ritter, analizzo il nodo B e attraverso l’equilibrio dei momenti rispetto al nodo C ricavo lo sforzo assiale
N1= -2F (il meno indica che il verso della freccia precedentemente ipotizzato di trazione, è di compressione quindi lo cambio). Eseguendo invece l’equilibrio dei momenti rispetto al nodo B ottengo lo sforzo assiale N3= 3/2 F (essendo positiva la forza, il verso della freccia ipotizzato è corretto, quindi di trazione). Infine eseguendo l’equilibrio alla traslazione verticale ottengo il valore dello sforzo assiale N2= F
/2dato dalla scomposizione dello sforzo N2 nelle sue due componenti orizzontale e verticale..jpg)
Avendo già determinato lo sforzo assiale N3, analizzo il nodo A eseguendo l’equilibrio alla traslazione orizzontale. Da questo ricavo il valore dello sforzo assiale N4= -3/2 F, dato dalla scomposizione nelle sue due componenti orizzontale e verticale. .jpg)
Infine studio l’ultima sezione di Ritter, quella che fa riferimento al nodo D e determino attraverso il momento rispetto al polo D e l’equilibrio alla traslazione verticale, gli ultimi due sforzi assiali N5= 5/2 F e N6= -F/2.
Attraverso il grafico elaborato dal software SAP, è possibile ottenere una conferma su quali siano i carichi conferiti a ciascuna asta e quali di queste siano compresse o tese. Ciò è possibile perché questo software ci permette di disegnare interamente la struttura assegnando alle singole aste i vincoli predisposti (cerniere, carrelli o incastri) nonché i carichi (distribuiti o concentrati) su qualsiasi trave o nodo. 
Il compito più grande svolto da SAP è di determinare la deformata qualitativa della struttura in esame che per strutture così semplici è abbastanza palese mentre per altre più complesse no.
Travatura reticolare asimmetrica
Lo scopo di questo esercizio è quello di risolvere una struttura reticolare asimmetrica attraverso il METODO DEI NODI, precedentemente enunciato.
Come per quella simmetrica, anche qui dobbiamo preventivamente verificare l’isostaticità della struttura.
V = L(gradi di vincolo = gradi di libertà)
V = Ve + Vi (Gradi di vincolo = vincoli esterni + vincoli interni)
2 (n-1) (n numero di aste che la cerniera collega)
Nodi A-G: 2 (2-1)= 2 x 2= 4
Nodi B-D-F: 2 (3-1)= 4 x 3= 12
Nodo E: 2 (4-1)= 6 x 1= 6
Nodo C: 2 (5-1)= 8 x 1= 8 quindi i gradi di vincolo interni sono: 30 Vi + 3 Ve = V V=L=33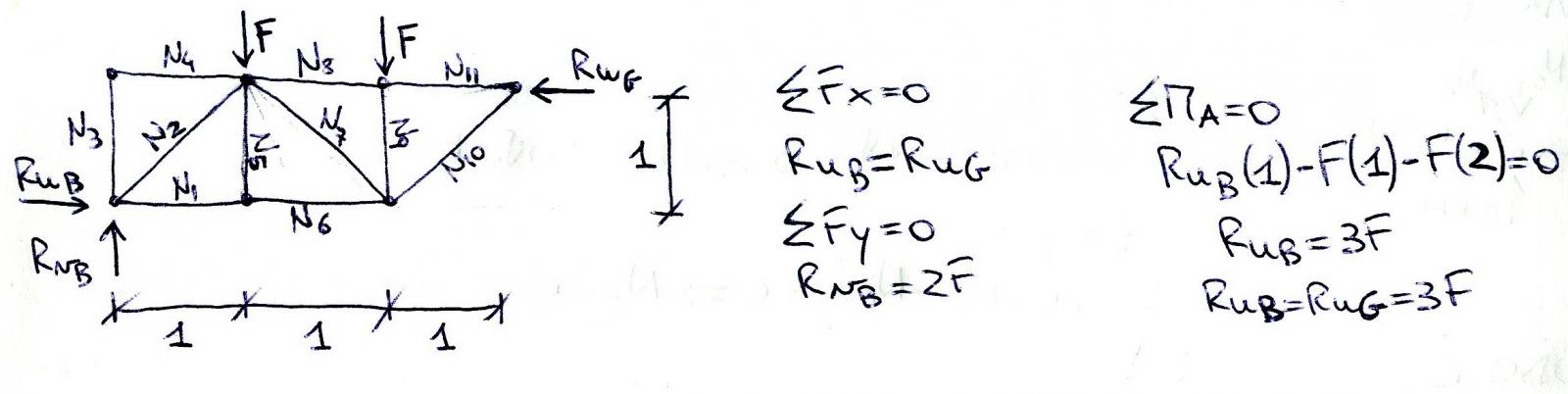
Ora possiamo procedere al calcolo delle reazioni vincolari attraverso gli equilibri alle traslazioni orizzontale e verticale e all’equilibrio dei momenti rispetto ad un polo prefissato. Dall’equilibrio alla traslazione orizzontale otteniamo che Rub=Rug quindi sappiamo che le due reazioni sono uguali e opposte; dalla traslazione verticale invece troviamo il valore di Rvb= 2F verso l’alto, quindi a bilanciare le due forze concentrate F, infine attraverso l’equilibrio dei momenti rispetto al polo in A stabiliamo il valore di Rub e Rug= 3F.
A questo punto, avendo calcolato tutte le reazioni vincolari, procediamo al calcolo delle azioni di contatto attraverso il METODO DEI NODI. Assegniamo a F il valore di 10KN e a L il valore di 1m. Ricordo che essendo una travatura reticolare, le azioni di contatto che andremo a calcolare saranno tutti sforzi normali N.
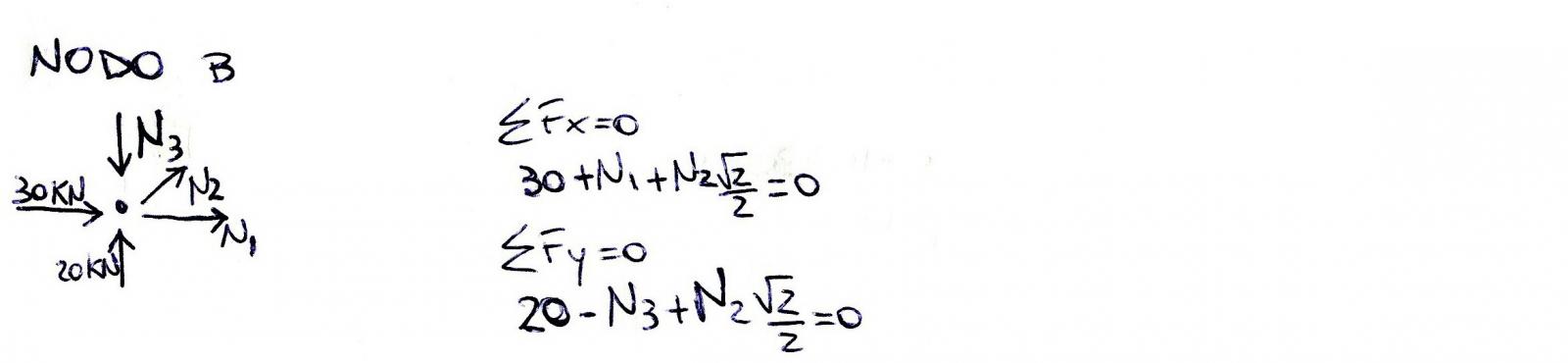
Partiamo dal nodo B perché sono note le reazioni vincolari Rub (30KN) e Rvb (20KN) e facciamo gli equilibri alle traslazioni orizzontale e verticale per determinare gli sforzi N1, N2 e N3. Eseguendo i calcoli ci rendiamo subito conto che non è possibile ottenere dei risultati perchè i due equilibri (traslazione orizzontale e verticale) prevedono due sistemi ognuno in due incognite quindi irrisolvibile. .jpg)
Proviamo quindi con il nodo G, altro nodo dove insiste la reazione vincolare Rug (30KN) e qui notiamo che per l’equilibrio alla traslazione verticale abbiamo solo la componente verticale dello sforzo assiale N10 che non è bilanciata da alcuna forza quindi il suo contributo è 0 sia in direzione orizzontale che verticale, ovvero l’asta è SCARICA (N10= 0). A questo punto possiamo facilmente calcolare lo sforzo N11= 30KN..jpg)
Procedendo verso sinistra vi è il nodo F dove abbiamo le due traslazioni, verticale e orizzontale, espresse ognuna con un sistema ad una incognita quindi banalmente risolvibile. Da questo infatti ricaviamo N8= 30KN e N9= 10KN..jpg)
Nel nodo E invece, scompongo lo sforzo assiale N7 nelle sue due componenti (orizzontale e verticale) ottenendo il valore di N7= 10KN e di conseguenza sfrutto la sua componente orizzontale pari a 10KN per calcolare lo sforzo assiale N6= -10KN (il meno, come al solito, indica che bisogna cambiare il verso della freccia). 
Il nodo D invece presenta nel suo equilibrio un’altra asta scarica, eseguendo infatti gli equilibri alle due traslazioni orizzontale e verticale, si ottengono N1= -10KN e N5= 0.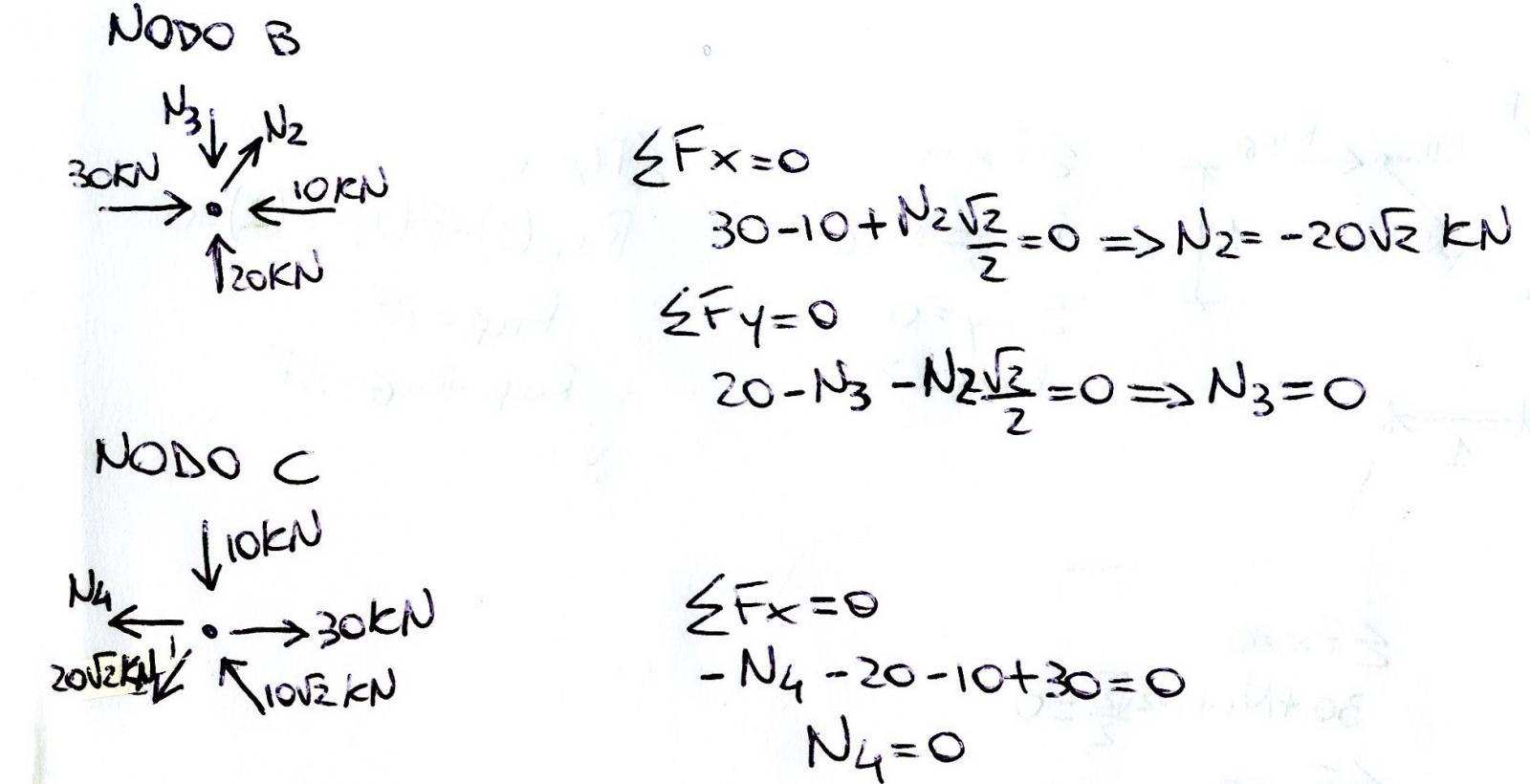 
Infine dal nodo B otteniamo altri due sforzi assiali N2= -20KN e N3= 0 mentre dal nodo C, ultima cerniera rimasta, deduciamo dai calcoli che N4= 0.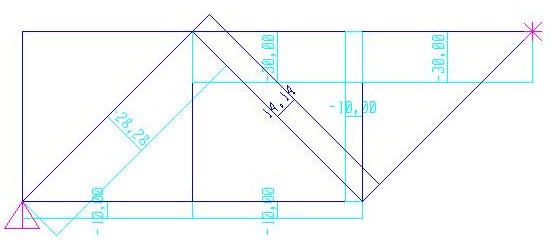 
Una volta determinati i valori di N su ogni singola asta, ridisegno la struttura su SAP facendo uso della griglia alla quale abbiamo precedentemente assegnato le campate lungo l’asse x (ascissa) e lungo l’asse z (ordinata) e i loro valori in metri. Impongo, fissati gli appoggi della travatura (cerniera e carrello), che ogni asta sia incernierata all’altra ma che venga impedita la trasmissione del momento da un’ asta all’altra. Infine assegno i carichi concentrati sui nodi C ed F e faccio partire l’analisi della deformazione.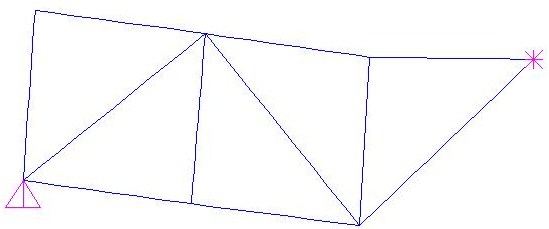 
Esercizi sugli archi a tre cerniere e vari
Esercizio n°1
In questo esercizio, è stata analizzata una “mensola” alla quale sono sovrapposti due carichi assiali: ql (carico concentrato all’estremo libero) e q (carico distribuito lungo la trave ma solo nel tratto che va dall’incastro fino a l). Come sappiamo i carichi concentrati e distribuiti danno risultati ben diversi che ora vedremo.
Per prima cosa notiamo che i gradi di vincolo e di libertà coincidono: v= l (3=3). Determiniamo quindi le reazioni vincolari che in questo caso sono molto semplici da calcolare in quanto, avendo solo forze assiali, non sono previsti l’equilibrio alla traslazione verticale e ai momenti perchè non gravano forze verticali o momenti concentrati sulla struttura.
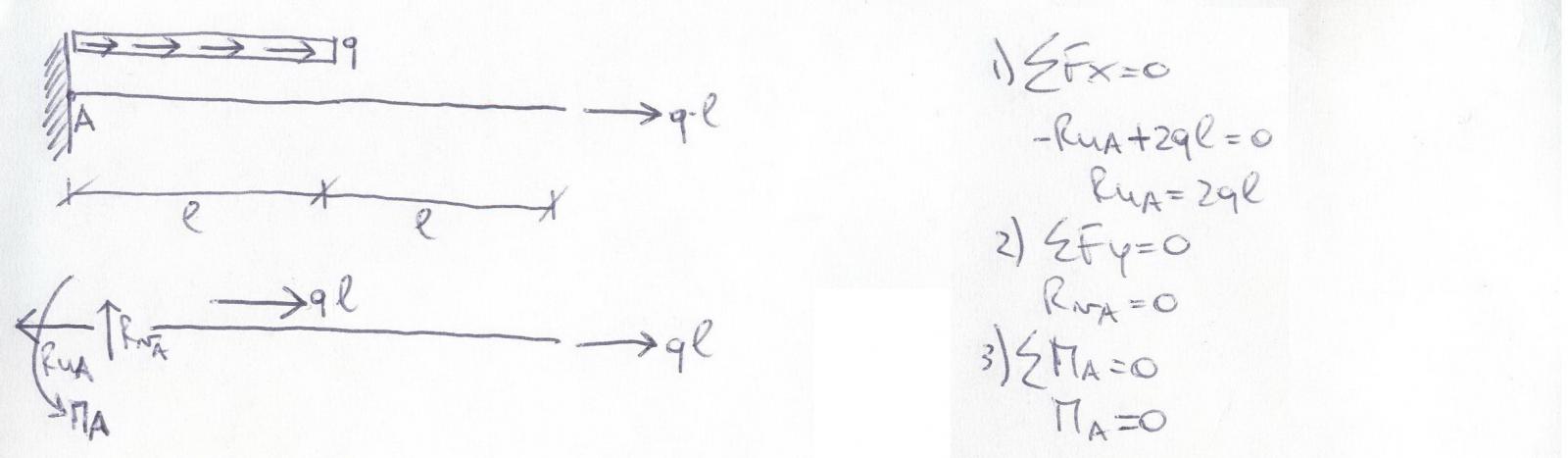
Dalle reazioni vincolari infatti otteniamo che dall’equilibrio alla traslazione orizzontale (ΣFx = 0) Rua= 2ql reazione derivante dall’incastro e atta ad equilibrare le due forze mentre dall’equilibrio alla traslazione verticale (ΣFy = 0) Rva= 0 perché non deve equilibrare alcuna forza verticale e così anche (ΣMa = 0) Ma=0.
Analizzando le azioni di contatto sulla trave possiamo quindi dire che l’unica tensione che si sviluppa all’interno della trave è quella Normale ed è N=2ql.
Analizzando la struttura ai “bordi”, notiamo che all’incastro la N= 2ql data dalla sovrapposizione del carico concentrato ql, che dà un grafico di N costante, e del carico distribuito q, che invece dà un grafico di N lineare in quanto varia dalla mezzeria all’incastro. All’estremo libero invece, lo sforzo normale è equilibrato da una sola forza di trazione, il carico concentrato ql, che determina di conseguenza un grafico costante di N su tutta la lunghezza della trave.
Esercizio n°2
L’argomento di questo esercizio è una trave su 3 appoggi con due momenti concentrati sull’appoggio centrale che tuttavia funge da cerniera quindi non permette il passaggio del momento flettente (o “di continuità”) e di conseguenza nemmeno la rotazione relativa, rotazioni uguali a sinistra e a destra della cerniera (φs=φd). Anche per questa struttura, essendo isostatica, v= l.
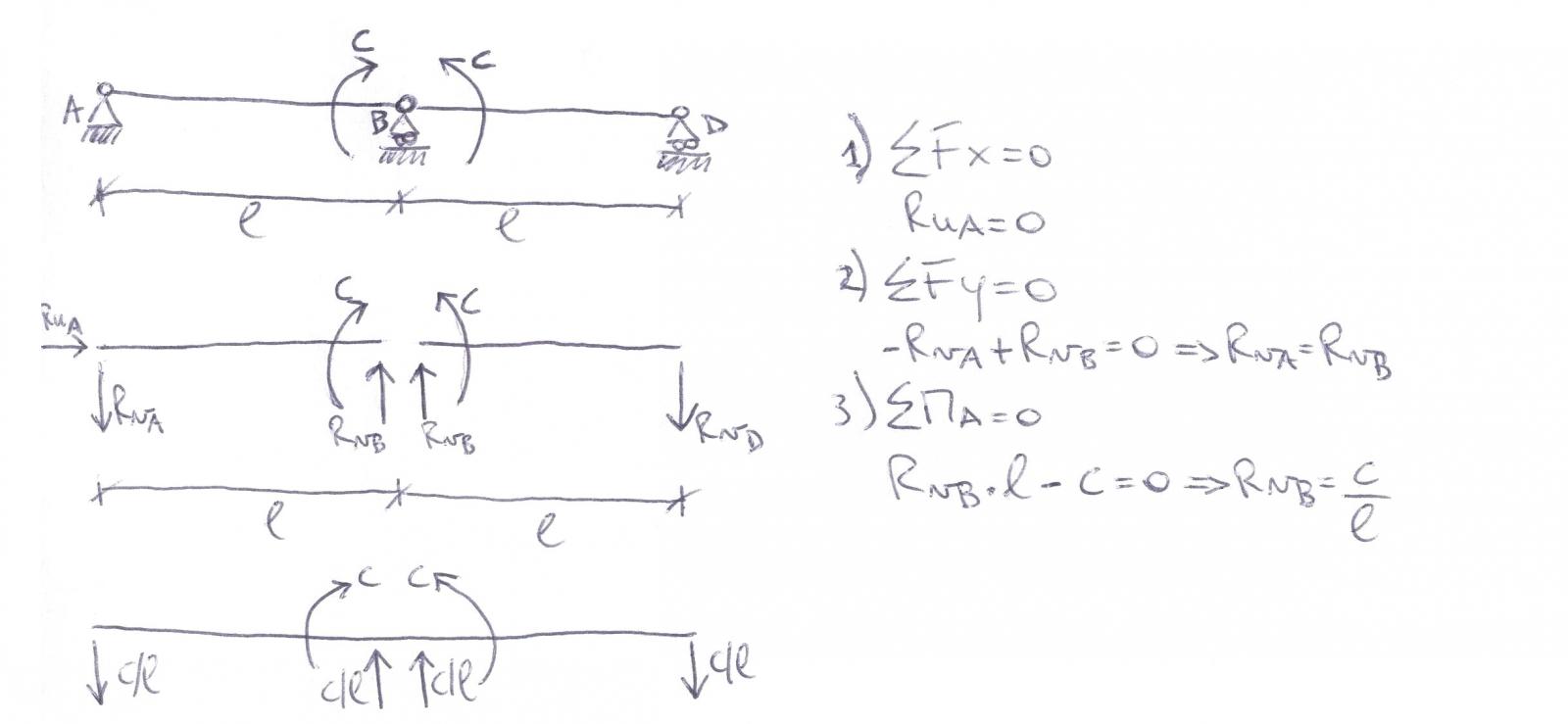
Dagli equilibri alle traslazioni orizzontali, verticali e di momento, otteniamo che Rua= 0 in quanto non insistono forze assiali sulla struttura; Rva= Rvb e Rvb= Rvd in quanto coppie di forze che controbilanciano i due momenti esterni c. La coppia Rva-Rvb è antioraria per controbilanciare c orario mentre la coppia Rvb-Rvd è oraria perché deve controbilanciare l’altro momento antiorario c. In valore assoluto Rva, Rvb e Rvd hanno tutte lo stesso valore c/l.
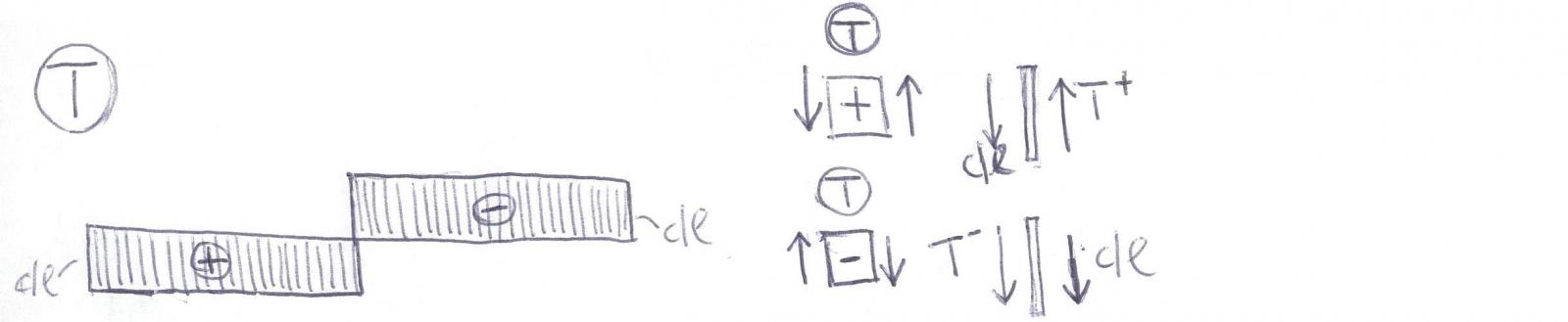
Dal grafico del taglio si può notare come vi sia un salto nel punto in cui sono concentrati i due momenti pari proprio a c, il valore del momento. Questo comporta nel grafico del momento un punto angoloso (di spigolo o “cuspide”) che corrisponde ad un cambio di pendenza in quanto punto di incrocio dei due momenti lineari negativi perché tendono le fibre superiori della trave.
Esercizio n°3
Analizziamo ora un arco a 3 cerniere con una forza concentrata F in mezzeria, ovvero sulla cerniera. Prima di svolgere l’esercizio però è necessario fare alcuni ragionamenti di carattere qualitativo che permettono di risolvere più facilmente e velocemente l’equilibrio della struttura.
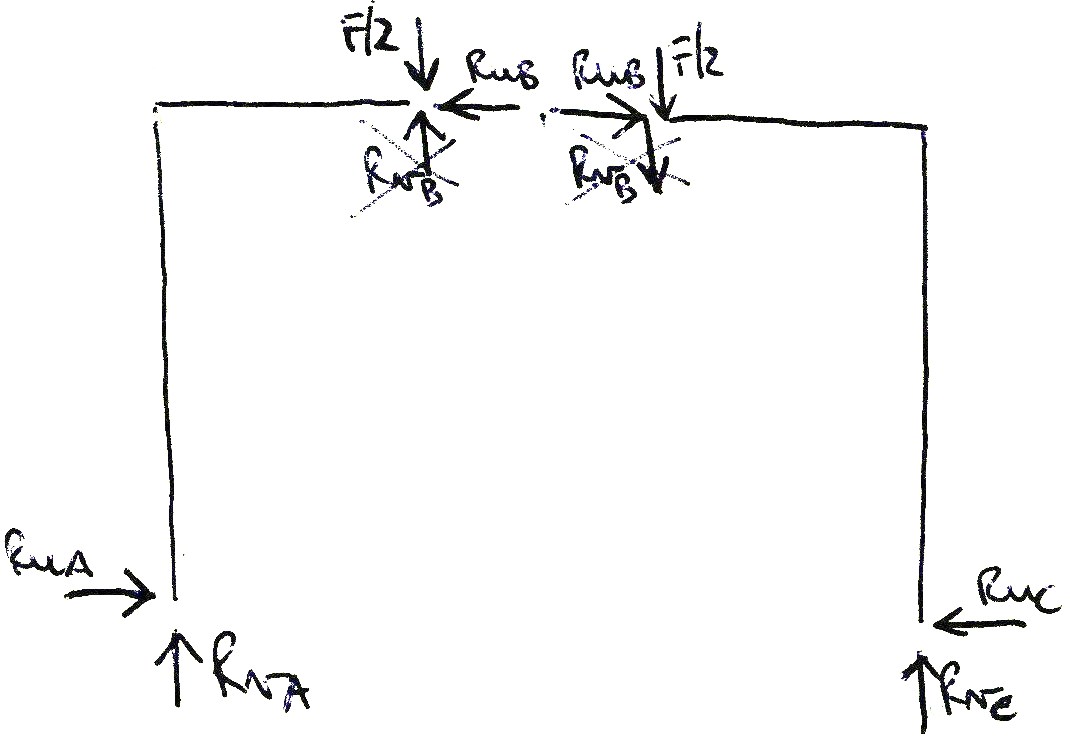
Come sappiamo, l’arco a tre cerniere è chiamato così perché presenta, oltre quelle alla base, anche una terza cerniera collocata sul tratto orizzontale che ci da 2 reazioni vincolari verticali e 2 orizzontali, tutte uguali e opposte. In questo caso però, essendo il portale simmetrico sia per geometria che per carico, la forza verticale F è equilibrata dalle sole 2 reazioni verticali date dalle 2 cerniere agli appoggi perché le reazioni della cerniera centrale essendo opposte causerebbero solo antisimmetria.
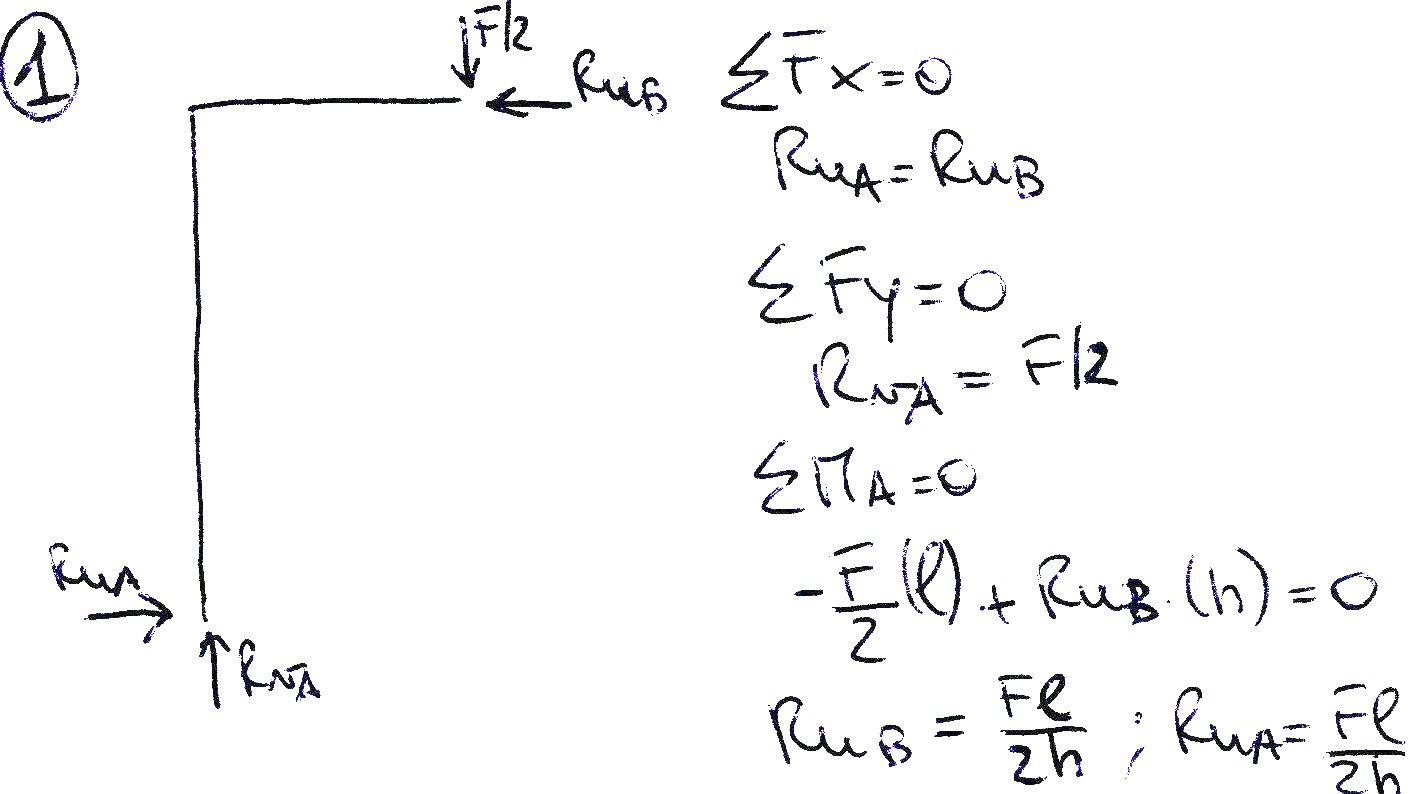
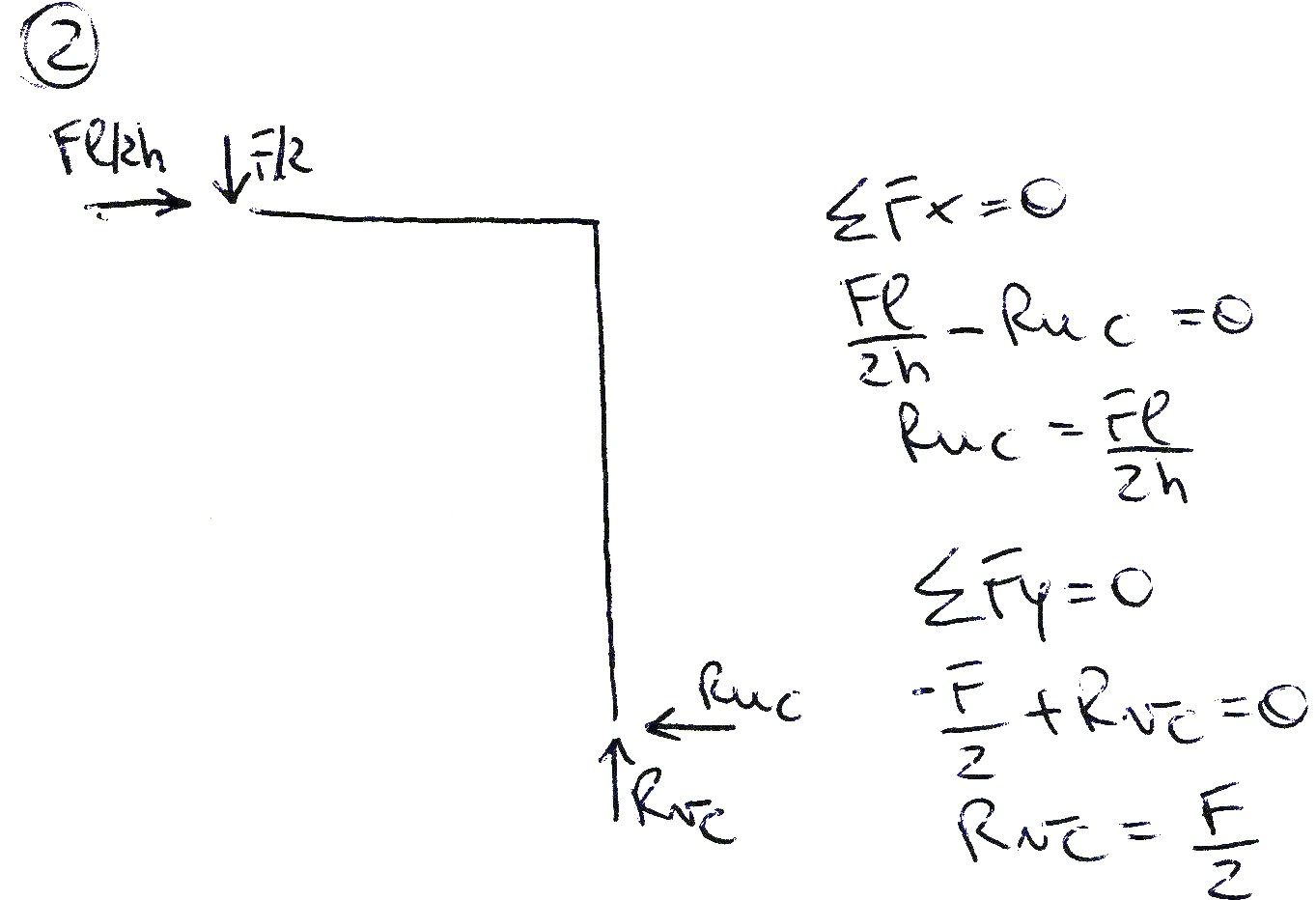
Spesso per le strutture come i portali, può risultare utile analizzare la struttura per porzioni più ridotte come in questo caso dove il portale, essendo simmetrico, è stato diviso a metà rendendo più semplice e rapido il calcolo delle reazioni vincolari. Dal primo corpo infatti troviamo che Rva= F/2, il risultato è giusto in quanto è l’unica reazione verticale che deve equilibrare la forza F/2 mentre dall’equilibrio dei momenti rispetto al polo A ricaviamo che Rub=Rua= Fl/2h. Questo ci fa capire che le reazioni orizzontali non sono nulle come invece si potrebbe pensare non essendoci carichi orizzontali; esse infatti servono ad equilibrare il momento orario generato dalla forza F per il braccio l/2. Allo stesso modo nel secondo corpo troviamo che Rub=Ruc= Fl/2h eRvc= F/2. Trovate le reazioni vincolari, analizziamo le azioni di contatto sul portale. Per fare ciò utilizziamo il metodo qualitativo dei “bordi”. Partendo infatti dalla cerniera in A troviamo che lo sforzo N è costante e di compressione in tutti i tratti ma assume il valore N= F/2 sui tratti verticali e N= Fl/2h sul tratto orizzontale. Anche il taglio presenta un grafico costante nei due tratti verticali pari a T=Fl/2h, positivo nel primo tratto verticale e negativo nel secondo; nel tratto orizzontale invece, vi è un grafico costante del taglio T=F/2, negativo nel primo tratto e positivo nel secondo mentre sulla cerniera, essendoci la forza concentrata F, vi sarà un salto pari alla forza F.
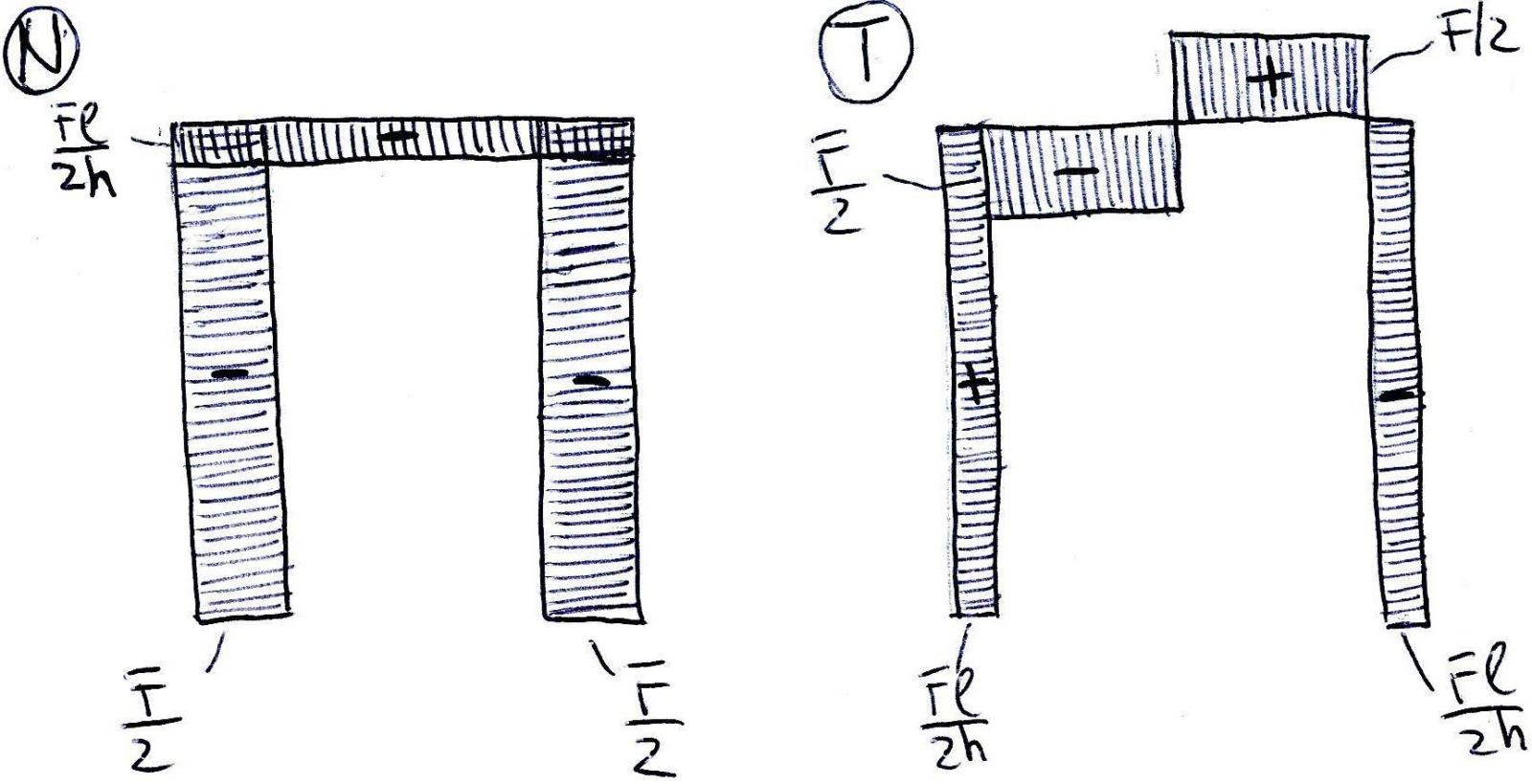
Infine nel grafico dei momenti vi sono andamenti lineari, dovuti ai grafici costanti del taglio, pari a M=Fl/2. I momenti sono tutti negativi in quanto tendono le fibre superiori e vi è un punto angoloso che coincide con la cerniera orizzontale che è dovuto al salto del taglio.
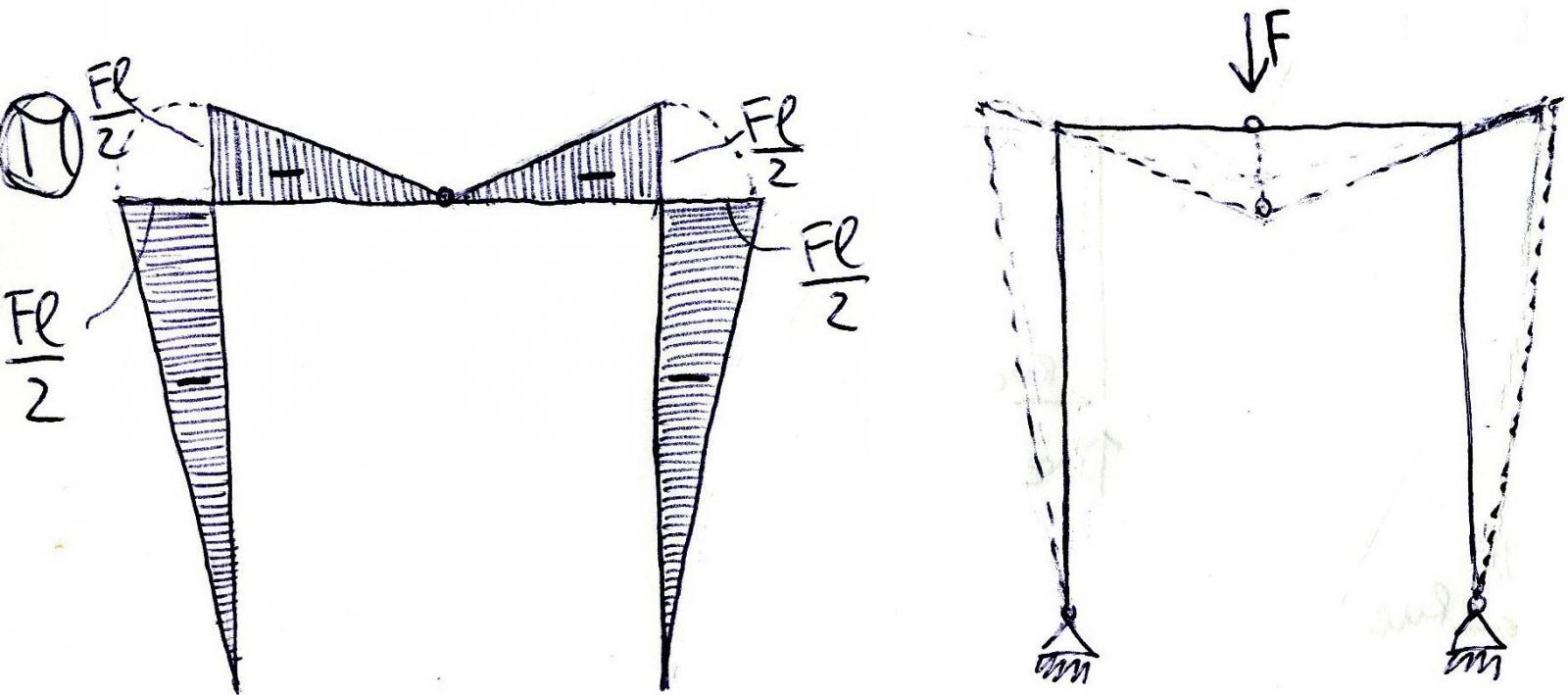
Attraverso il software di calcolo SAP è stato possibile riscontrare gli stessi risultati per le azioni di contatto e la deformata qualitativa. Questo infatti, essendo uno strumento immediato e semplice da utilizzare, spesso è stato utile anche come punto di partenza per risolvere strutture complesse che a mano avrebbero richiesto parecchio tempo. Non è il caso dei portali.
DEFORMATA QUALITATIVA GRAFICO DEL TAGLIO
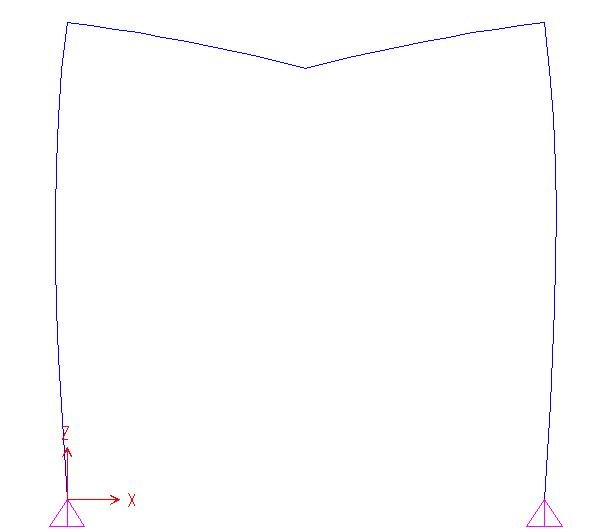
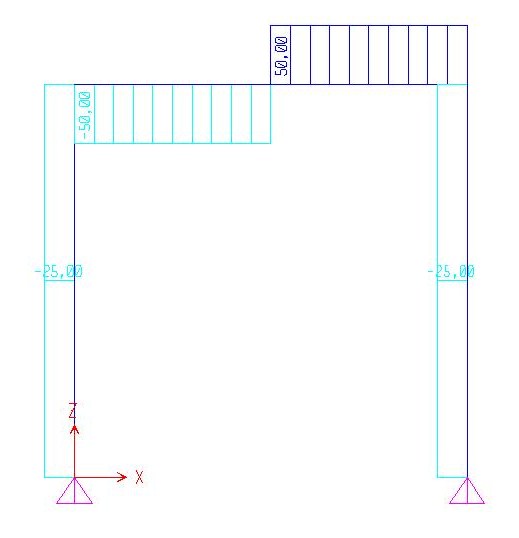
GRAFICO DELLA NORMALE GRAFICO DEL MOMENTO
Esercizio n°4
Svolto il portale con il carico concentrato in mezzeria, possiamo passare ad un portale più complesso per il quale assegneremo anche dei valori numerici al carico q e alle luci l e h.
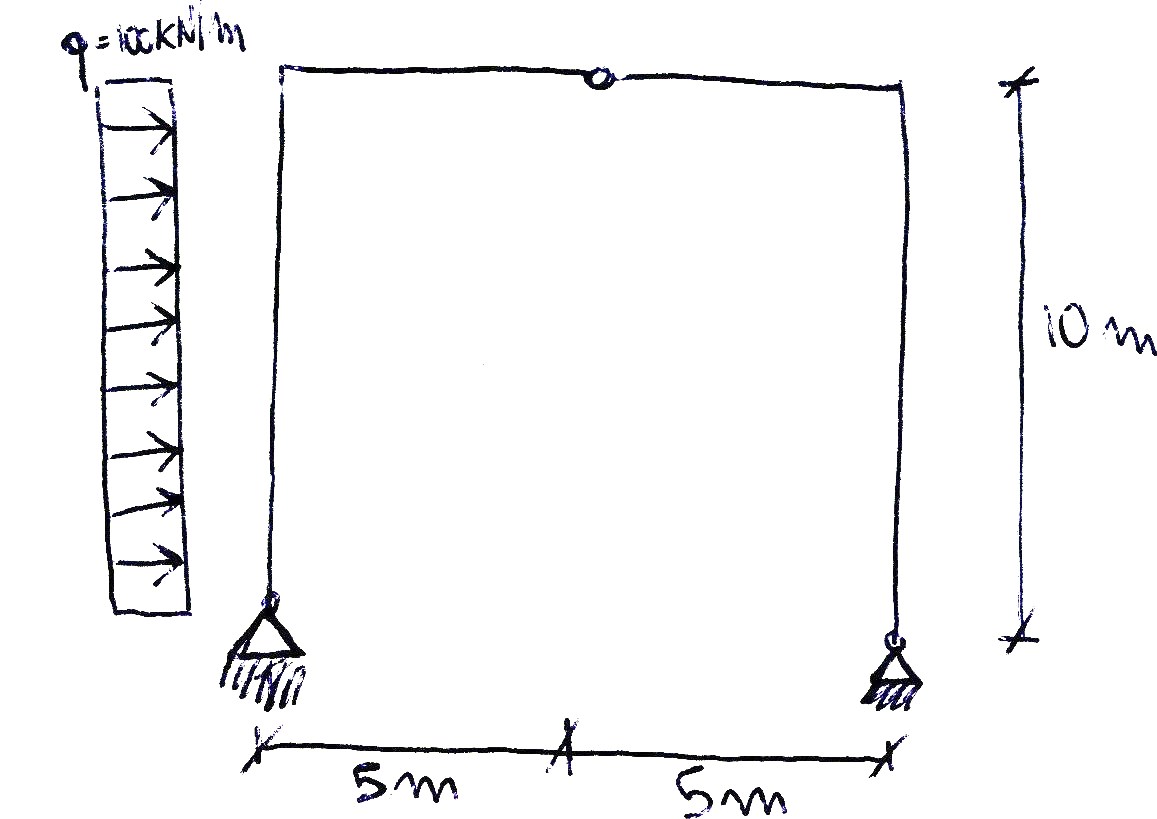q=100KN/m h=10m l=5m
In questo caso può essere utile analizzare il portale in due parti separate e farne l’equilibrio dei momenti rispetto ai poli A e B. Dai due equilibri ricaviamo che Ruc= 250KN e Rvc= 500KN.
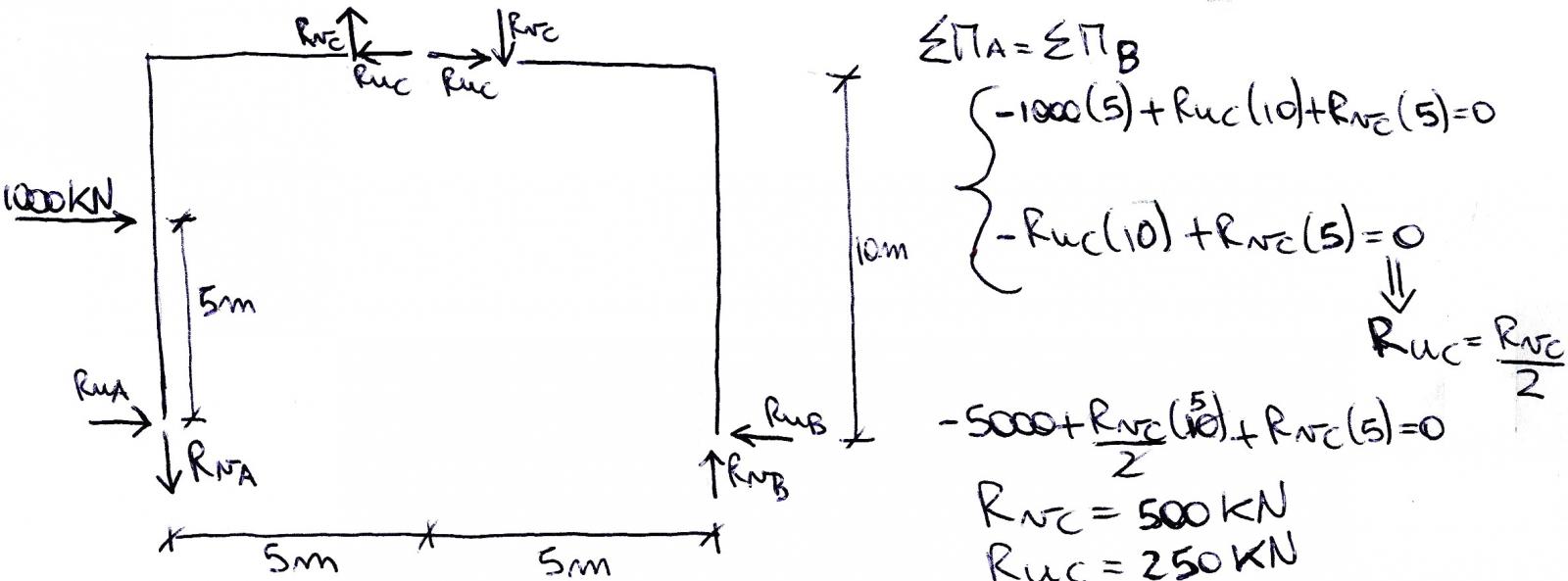
A questo punto, una volte determinate Ruc e Rvc, con le equazioni di equilibrio alle traslazioni verticali e orizzontali dei due corpi, posso ricavare velocemente Rva, Rua, Rvb e Ruc.
Dall’equilibrio alla traslazione orizzontale del primo corpo ottengo infatti che:
Rua= 1000-Ruc (250KN)= 750KN mentre dall’equilibrio alla traslazione verticale ottengo che
-Rva= Rvc (500KN) quindi anche Rva=500KN.
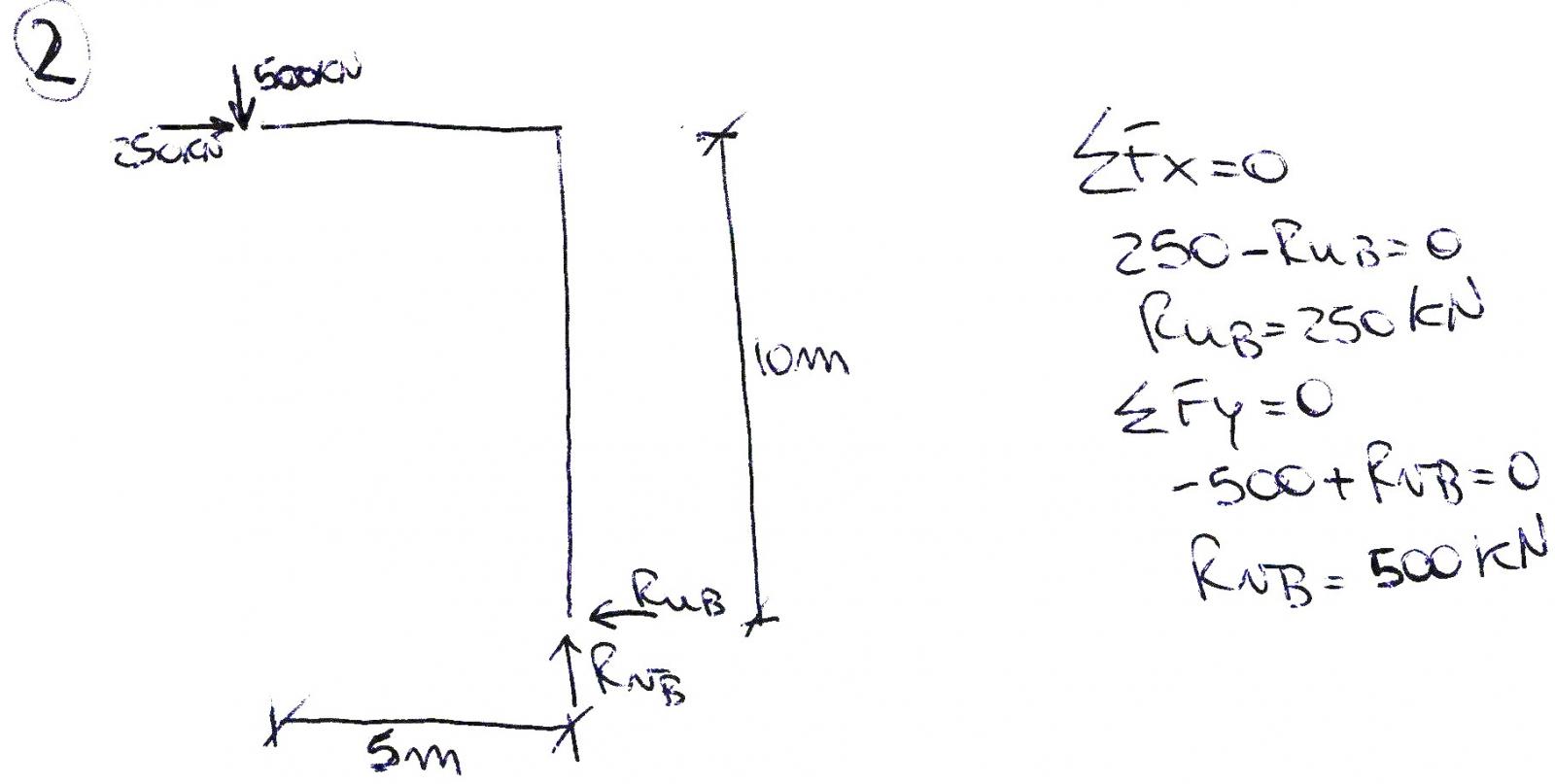
Dall’equilibrio alla traslazione orizzontale del secondo corpo ottengo che:
Ruc (250KN)= -Rub quindi Rub= 250KN mentre dall’equilibrio alla traslazione verticale ottengo che –Rvc (500KN)= Rvb quindi anche Rvb= 500KN.
Ultimo step sono le azioni di contatto dalle N,T e M. Dallo sforzo normale otteniamo un valore costante per i tratti ascendenti pari a N= 500KN positivo nel primo tratto e negativo nel secondo, mentre in quello orizzontale lo sforzo normale è costantemente positivo e pari a N= 250KN. Dal grafico del taglio invece otteniamo dei grafici più particolari, nel primo tratto verticale infatti il grafico ha un andamento lineare o “a farfalla”, effetto del carico distribuito che assume in A il valore T= 750KN e al nodo T= 250KN. Sul tratto orizzontale invece l’andamento è costante ed è pari a T=500KN mentre sul secondo tratto verticale il taglio assume un valore negativo pari a T=250KN.
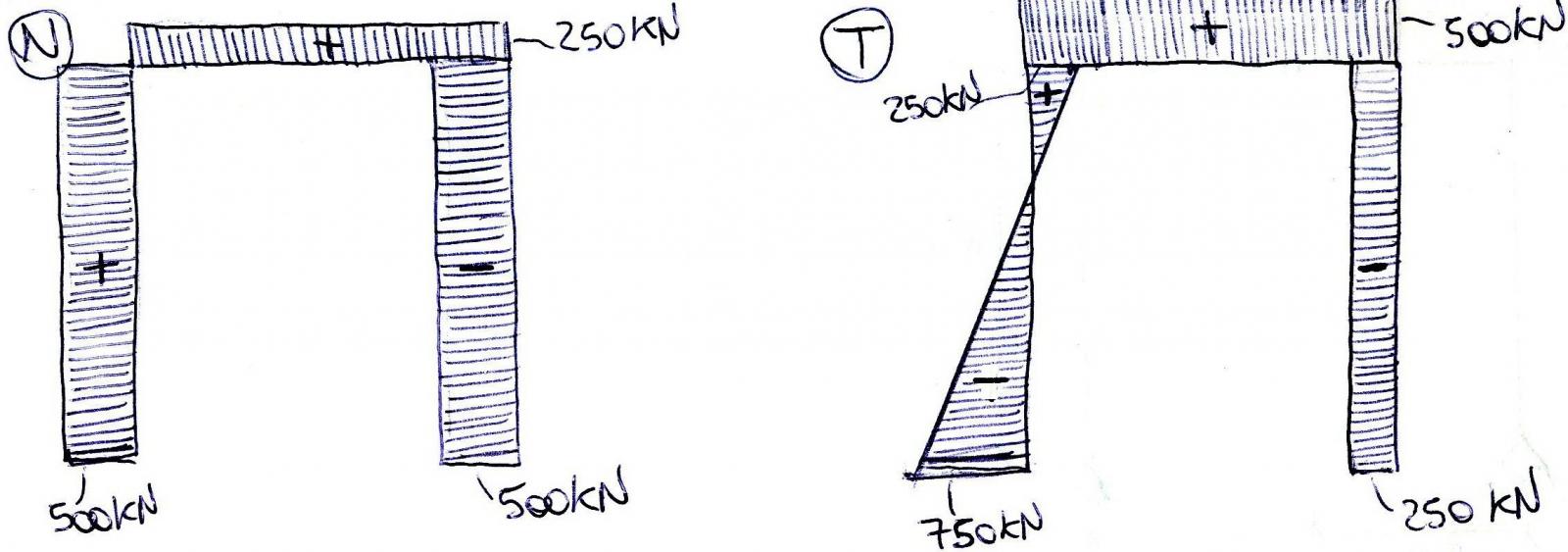
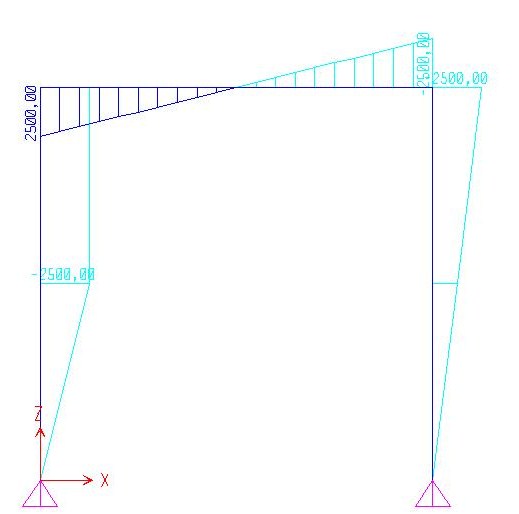
Il momento invece presenta un andamento parabolico positivo (fibre tese sotto) nel primo tratto verticale e il valore massimo lo assume dove il taglio è nullo (perché il momento è la derivata del taglio) mentre al nodo termina con un valore di M= 2500KN che viene ribaltato sul tratto orizzontale dove invece l’andamento è a farfalla. Infine sul secondo tratto verticale vi è un andamento lineare negativo (fibre tese sopra) che mantiene al nodo il valore di M= 2500KN e che rappresenta la continuità tra tratto orizzontale e verticale.
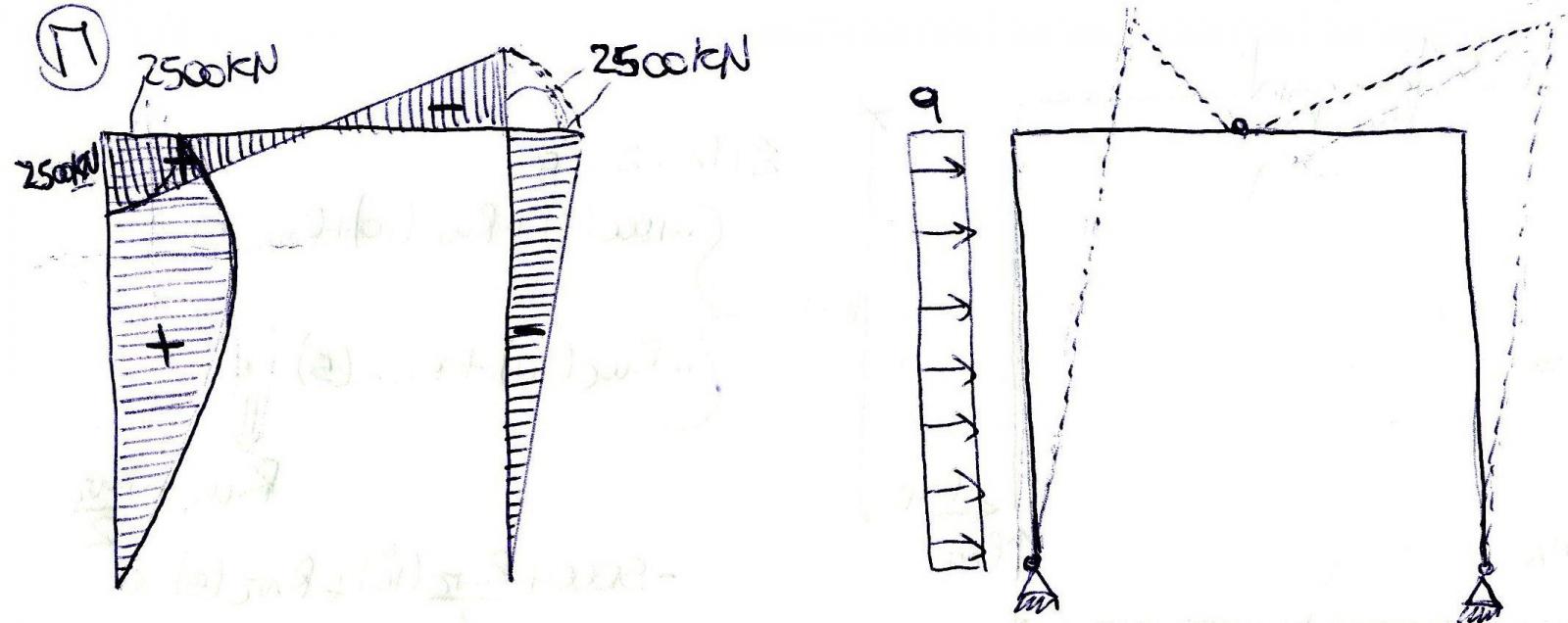
DEFORMATA QUALITATIVA GRAFICO DELLA NORMALE
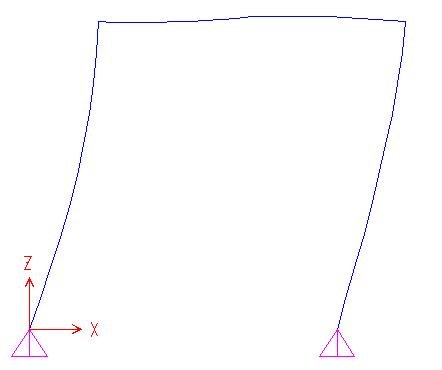
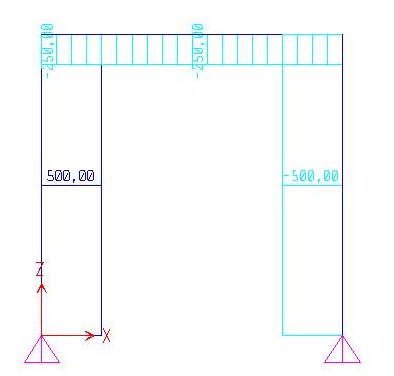
GRAFICO DEL TAGLIO GRAFICO DEL MOMENTO
Esercizio n°5
Come per il portale con un carico distribuito, analizziamo adesso il portale con due forze concentrate F.
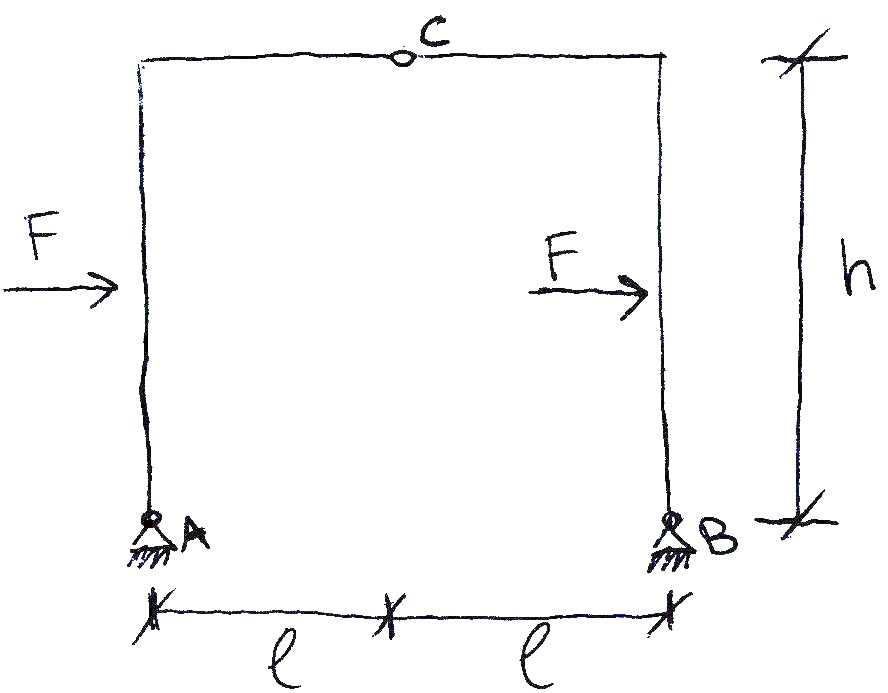
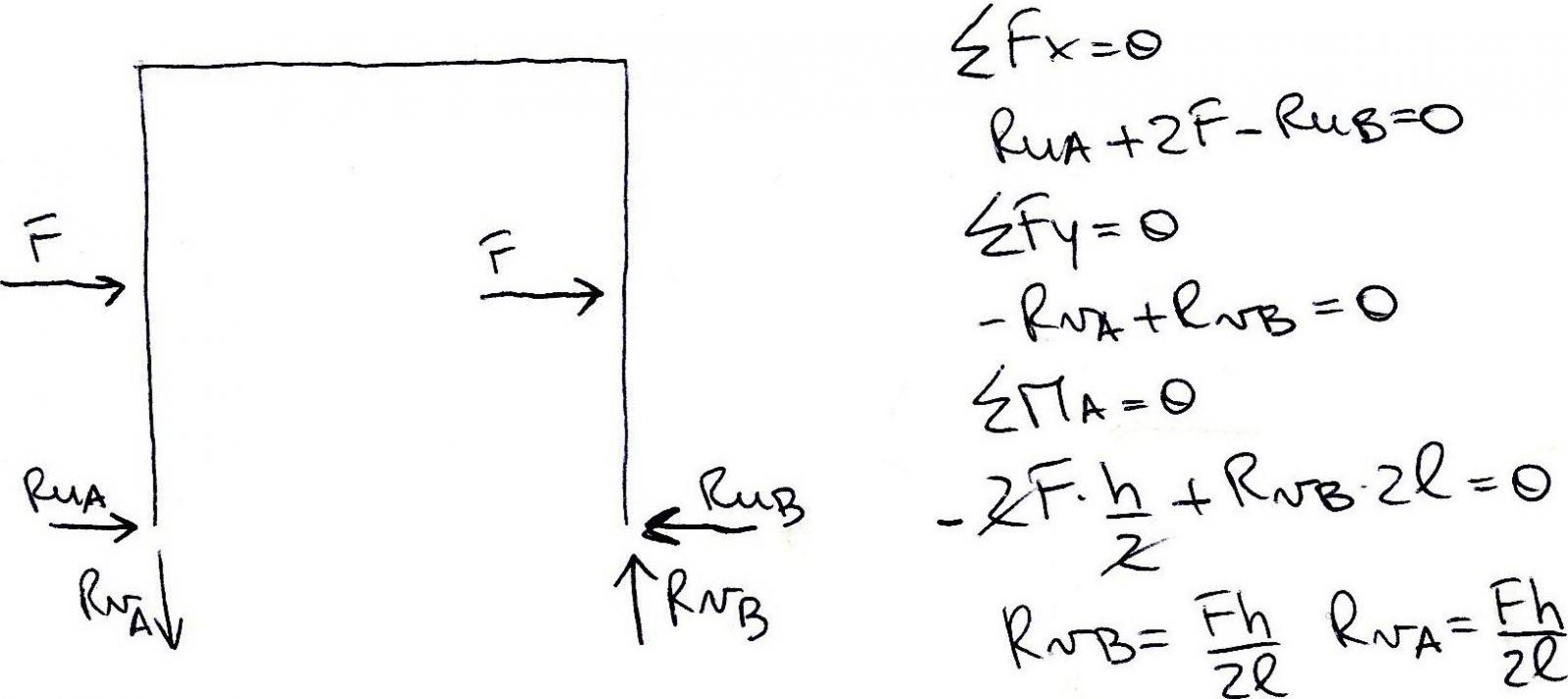
Anche per questa struttura è vantaggioso analizzare le due parti che la compongono separatamente ma solo per le reazioni orizzontali Rua, Rub e Ruc. Infatti per le reazioni verticali Rva e Rvb, non dovendo controbilanciare alcuna forza, è possibile fare il solo equilibrio dei momenti rispetto ad un polo scelto (A in questo caso) e determinare i valori delle singole reazioni. Rva=Rvb= Fh/2l.
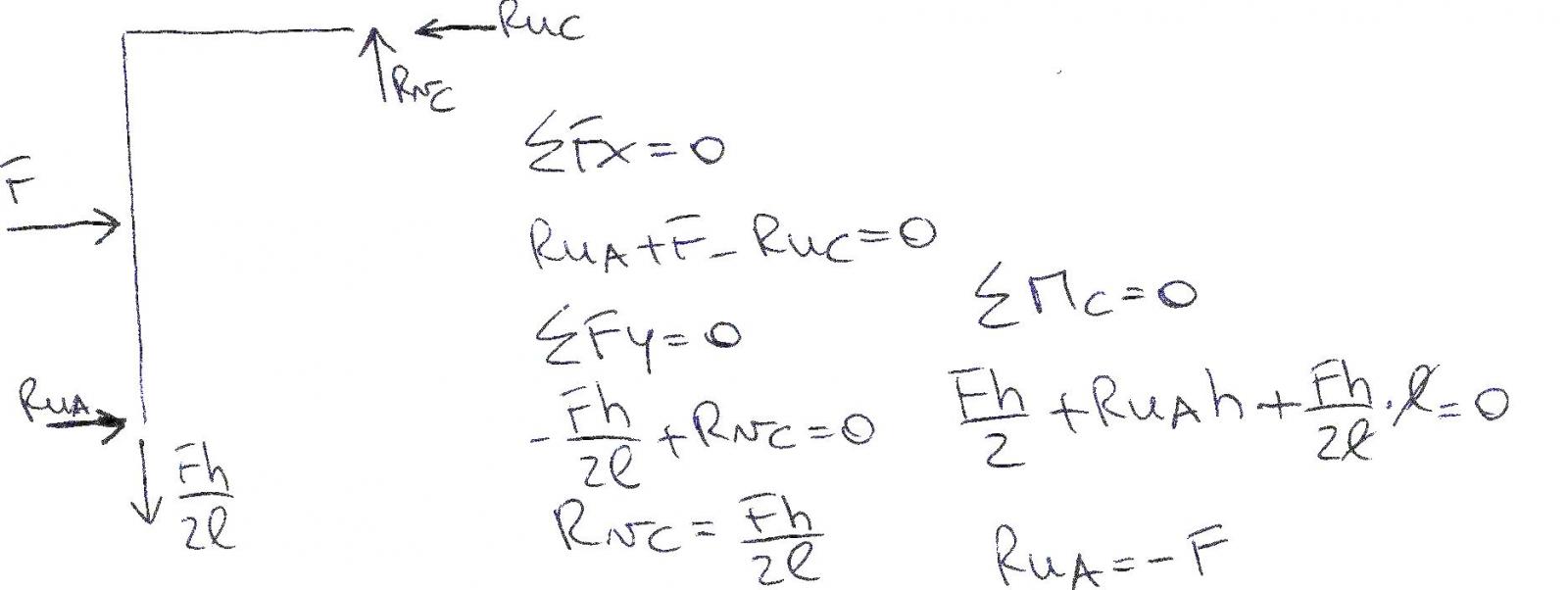
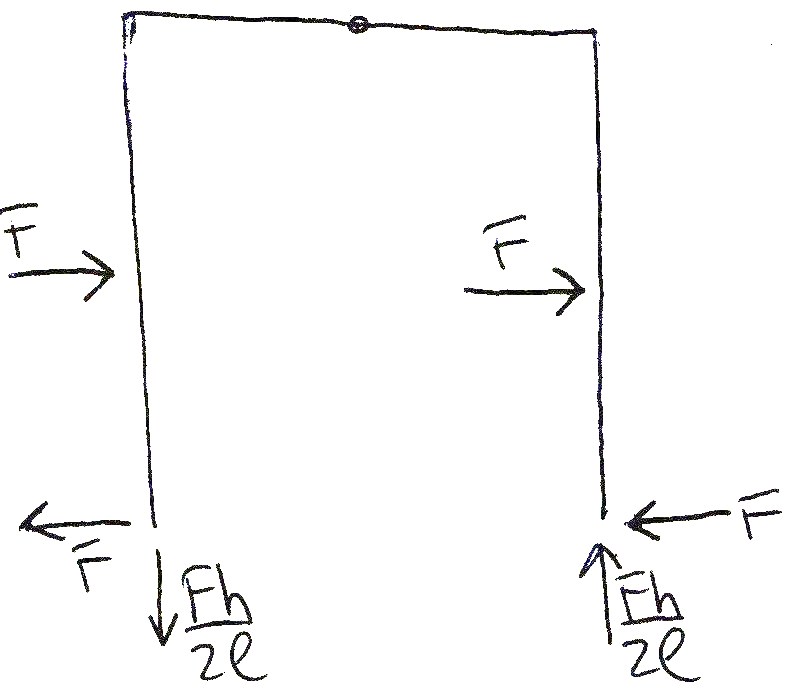
Dalla prima parte otteniamo che Rvc (reazione della cerniera interna)= Fh/2l ad equilibrare la reazione Rva. Invece dalla sommatoria dei momenti rispetto al polo C ricaviamo la reazione Rua= -F quindi cambio il verso che è giustamente opposto a quello della forza F. Per il secondo tratto della struttura andrà fatto lo stesso ragionamento della prima parte ricavando l’ultima reazione incognita che è Rub= F.
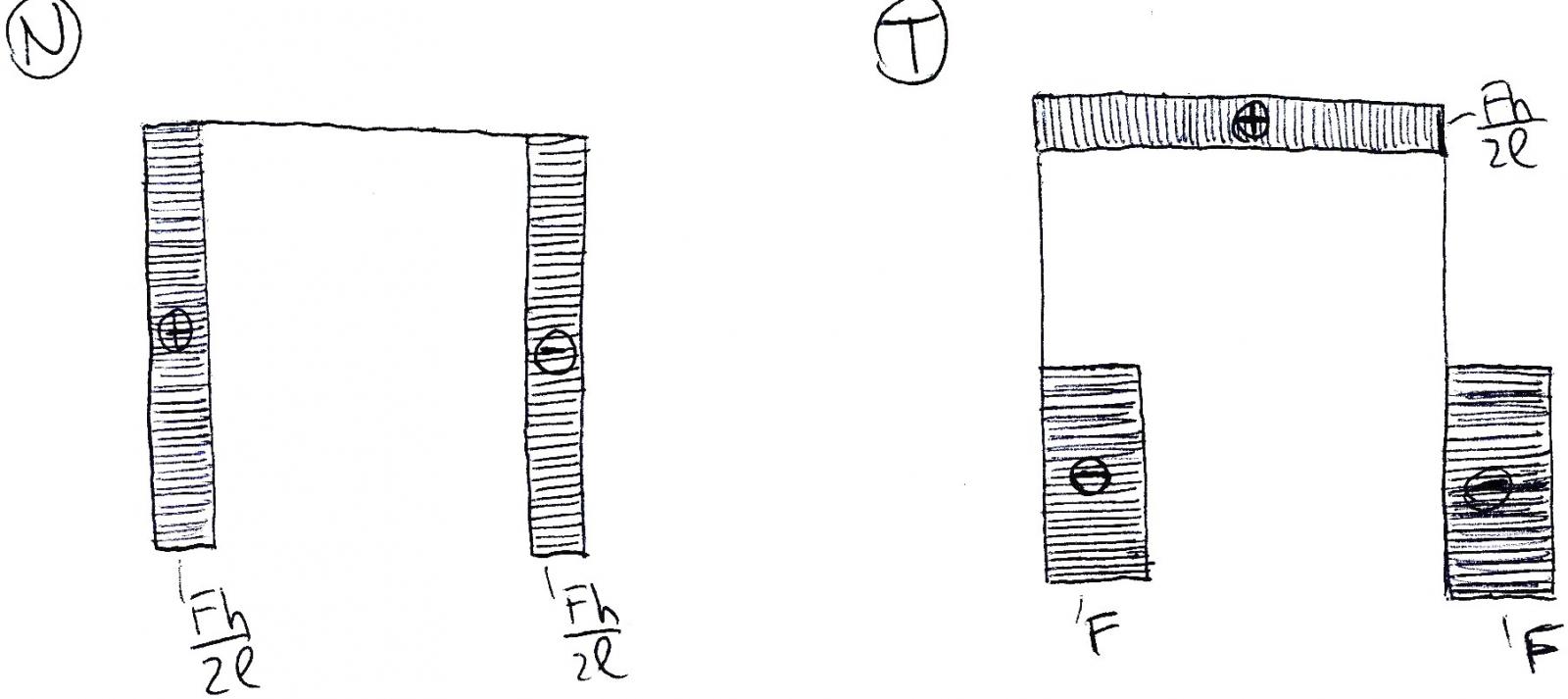
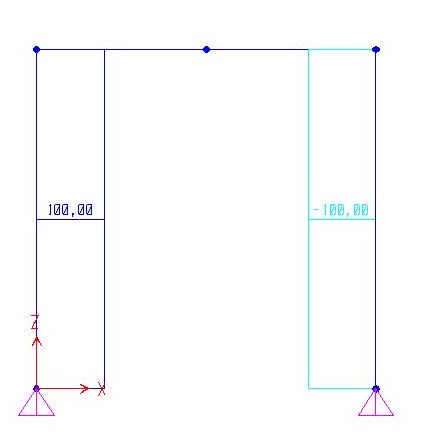
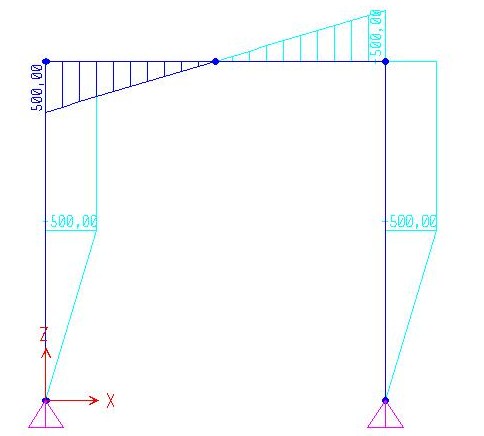
Dai grafici delle azioni di contatto notiamo che i due tratti verticali sono sollecitati da uno sforzo N= Fh/2l pari alle reazioni vincolari Rva e Rvb. Il primo positivo perché di trazione, il secondo negativo di compressione. Sul tratto orizzontale non vi sono sforzi normali in quanto non vi sono forze che agiscono sull’asse della trave e le due forze F concentrate sono applicate ad h/2 creando così un salto nel grafico del taglio. Rua e Rub generano un grafico di T costante e negativo ma fino ad h/2 dove le forze concentrate F generano il salto. Sul tratto orizzontale invece il taglio è costantemente T= Fl/2h ed è generato dalla coppia Rva e Rvb.
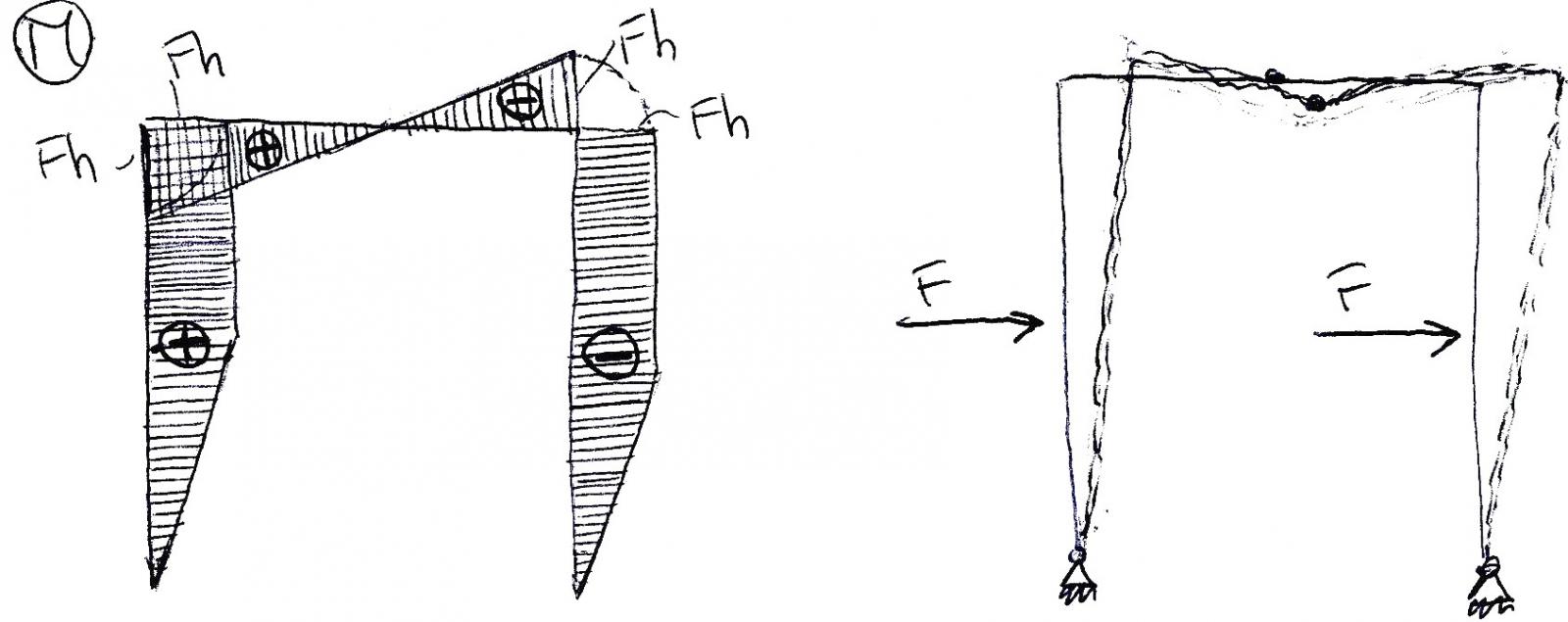
Analizzando invece il grafico dei momenti riscontriamo sui tratti verticali un andamento lineare da 0 ad h/2 che corrisponde ad un grafico costante del taglio, ad h/2 avviene il salto nel taglio quindi un punto di spigolo nel grafico dei momenti che implica un cambio di pendenza della retta che diventa verticale assumendo un valore di M= Fh. Sul tratto orizzontale invece il momento si annulla nella cerniere interna e assume un andamento a farfalla del valore di M=Fh e tendendo le fibre inferiori nel primo tratto e superiori nel secondo.
DEFORMATA QUALITATIVA GRAFICO DEL TAGLIO
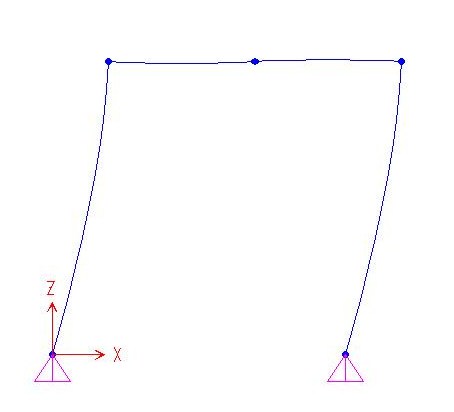
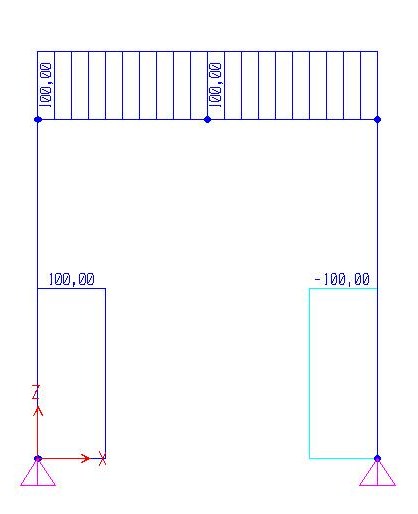
GRAFICO DELLA NORMALE GRAFICO DEL MOMENTO
Esercizio n°6
Per terminare lo studio sui portali analizziamo invece un particolare arco a 3 cerniere chiamato “portale zoppo” (ovvero le cui altezze variano nei due tratti verticali).
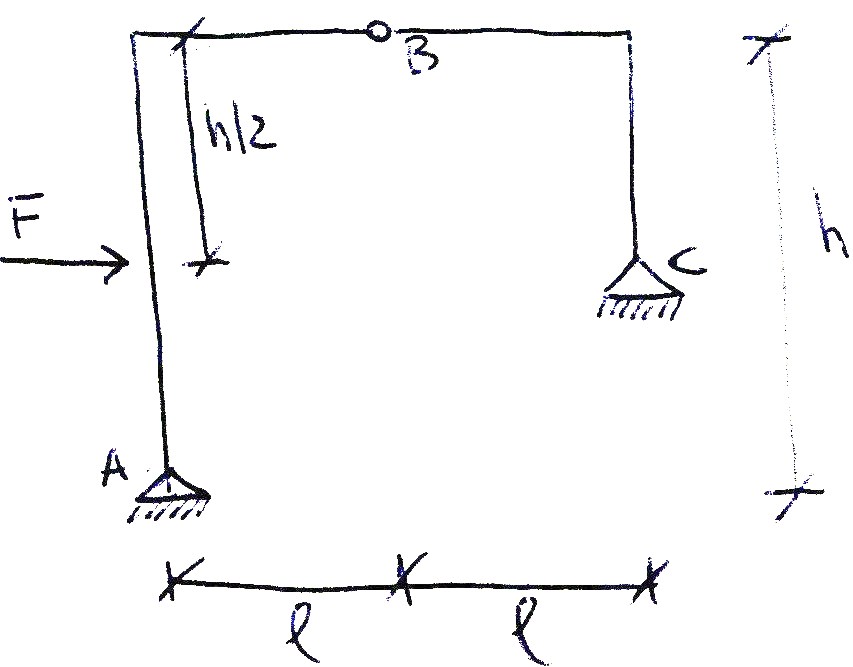
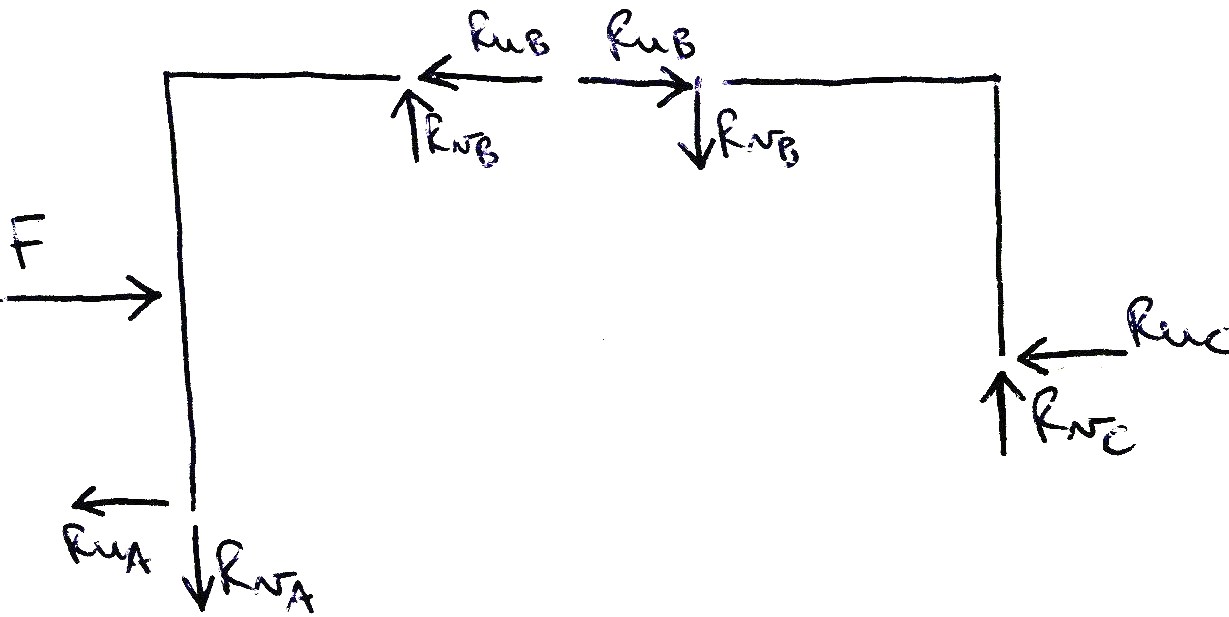
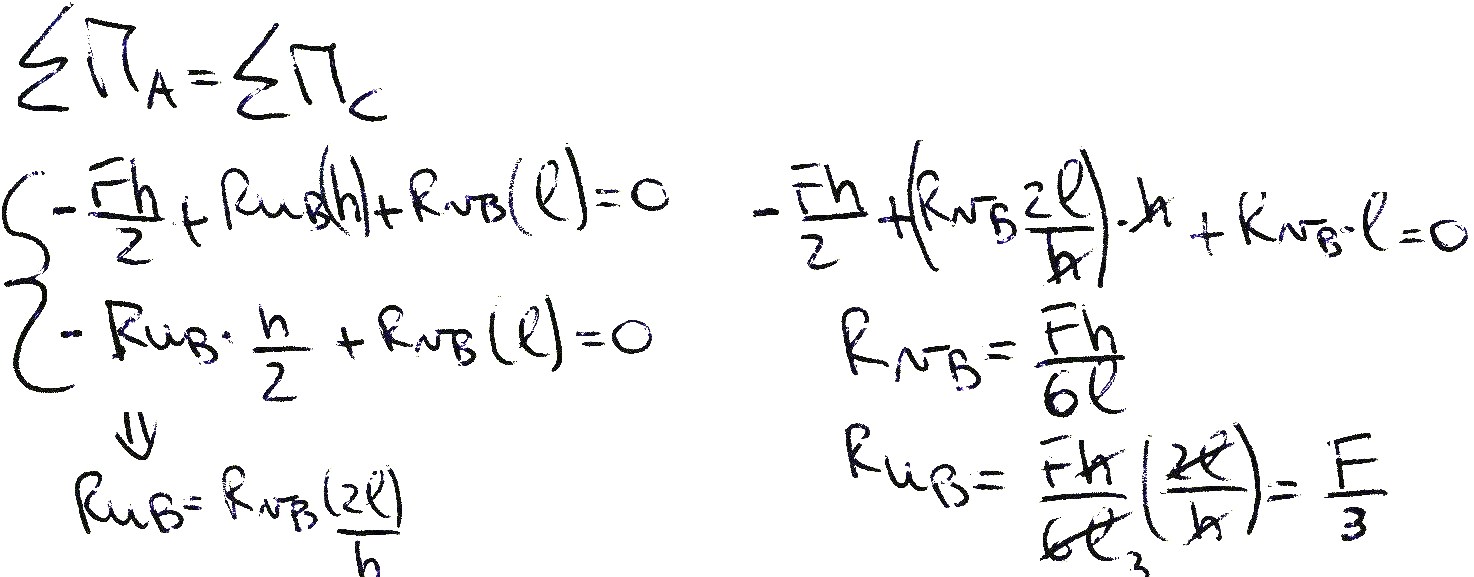
Per determinare le reazioni vincolari sono stati eseguiti due equilibri ai momenti rispetto ai poli A e C che messi a sistema hanno reso più semplice il calcolo delle reazioni vincolari della cerniera centrale, Rub e Rvb. Una volte determinata Rvb, i corpi sono stati analizzati separatamente e quindi attraverso l’equilibrio alla traslazione verticale è stato possibile determinare i valori delle altre due reazioni Rva e Rvc entrambe di valore Fh/2l. Anche per le reazioni orizzontali i corpi sono stati studiati separatamente infatti dall’equilibrio alla traslazione orizzontale del primo corpo abbiamo ottenuto Rua= 2/3F; mentre dall’equilibrio alla traslazione orizzontale del secondo corpo la reazione Ruc è proprio uguale a Rub, Rub=Ruc= F/3.
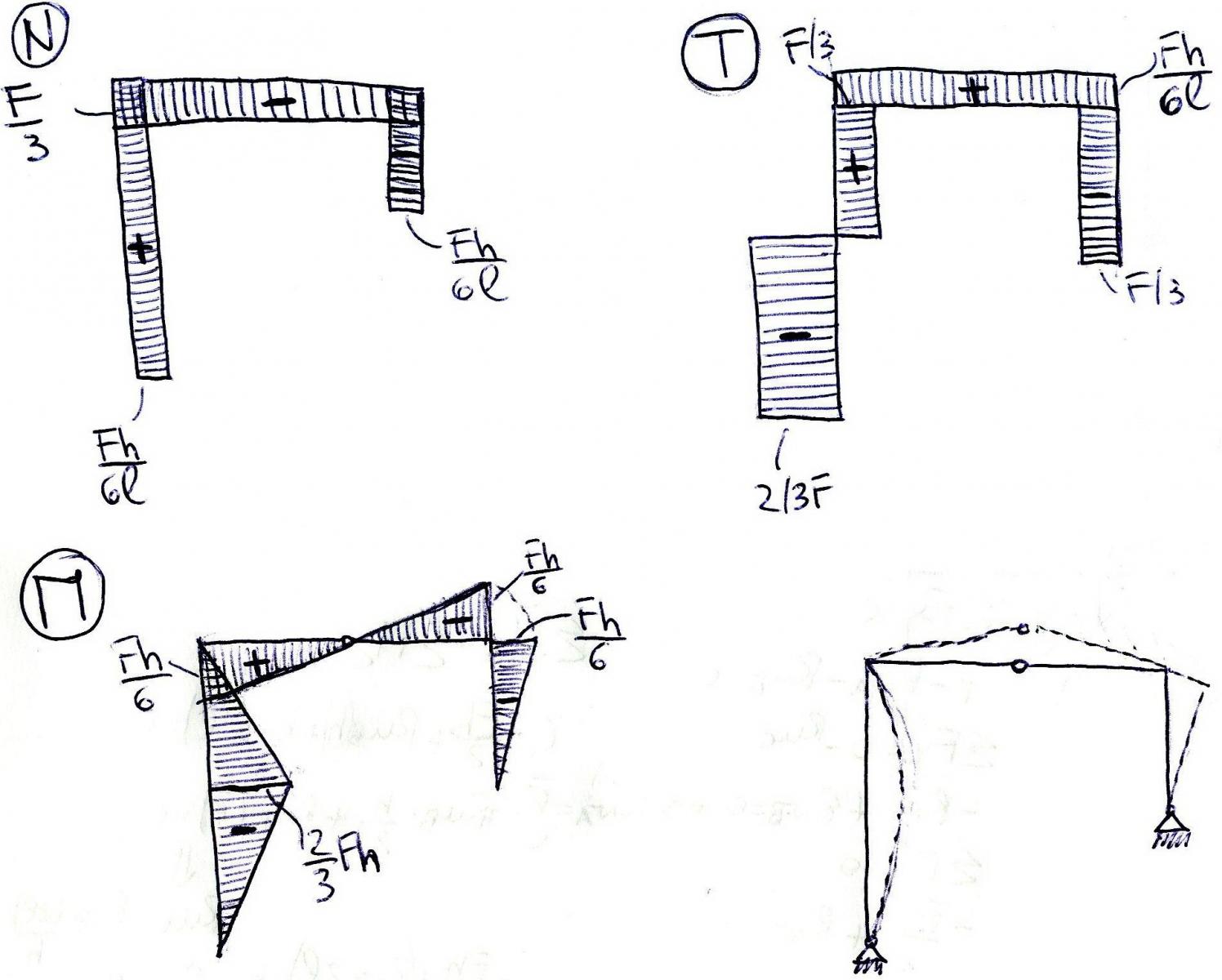
Come si nota dal grafico delle azioni di contatto, nella struttura in esame si genera un sforzo Normale costante pari Fh/6l di trazione nel primo tratto e di compressione nel secondo. Sul tratto orizzontale invece il valore di N è negativo perché di compressione e pari a F/3.
Nel grafico del Taglio invece è facilmente distinguibile il salto dovuto alla forza concentrata F applicata ad h/2 che da un T= -2/3F e un T= F/3 mentre sul tratto orizzontale il grafico è costantemente positivo e pari a T= Fh/6l mentre sul secondo tratto verticale è pari a T= F/3.
Nei portali in ultima analisi possiamo quindi dire che gli sforzi Normali verticali diventano di Taglio sui tratti orizzontali e viceversa per la continuità del nodo. Allo stesso modo i momenti assumono gli stessi valori nei nodi perché sono proprio questi i punti dove il momento flettente viene trasferito da un tratto orizzontale ad uno verticale.
Il punto più interessante nel grafico dei Momenti coincide con il punto in cui avviene il salto nel Taglio che causa nel grafico dei momenti un punto angoloso o di cuspide e quindi un cambio di pendenza della retta o meglio di derivata nulla.
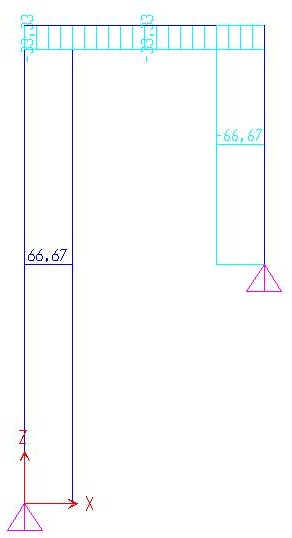
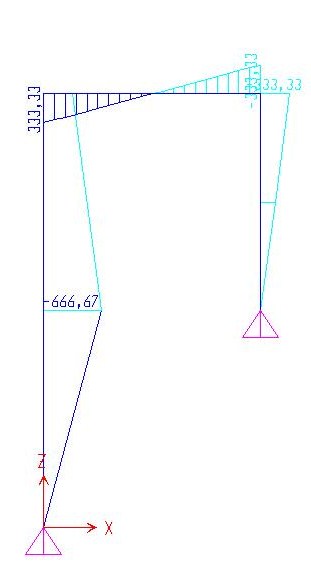
DEFORMATA QUALITATIVA GRAFICO DEL TAGLIO
GRAFICO DELLA NORMALE GRAFICO DEL MOMENTO
Esercitazione 2
L’argomento di questa esercitazione è il progetto di una trave dimensionata con il sussidio del foglio elettronico excel da cui ho potuto ricavarne un dimensionamento adeguato. L’edificio scelto è il progetto di Laboratorio 1 di una casa unifamiliare a Fiumicino e ho stabilito di progettare la trave del solaio maggiormente sollecitata nei tre materiali: legno, acciaio e cls.
SOLAIO IN LEGNO
Per questo tipo di solaio i passi da eseguire sono i seguenti:
1)calcolo di tutti i carichi che gravano sulla trave (Qs, Qp e Qa)
2)calcolo delle dimensioni del travetto in legno a partire da un dato ipotizzato, la base e relativa verifica.
3)calcolo delle dimensioni della trave in legno a partire da un dato ipotizzato, la base e relativa verifica.
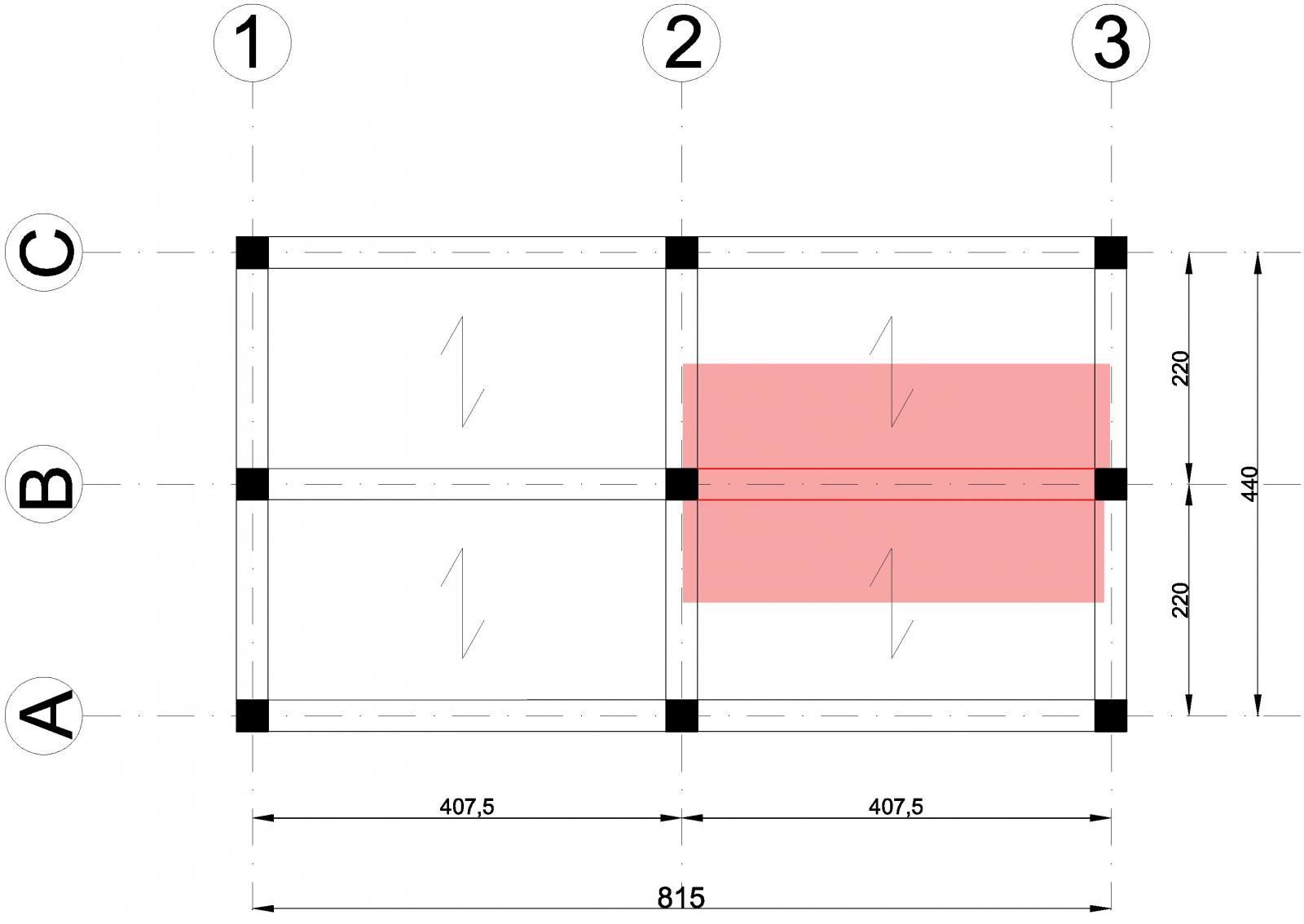
Progetto della Trave sull’allineamento B2-B3
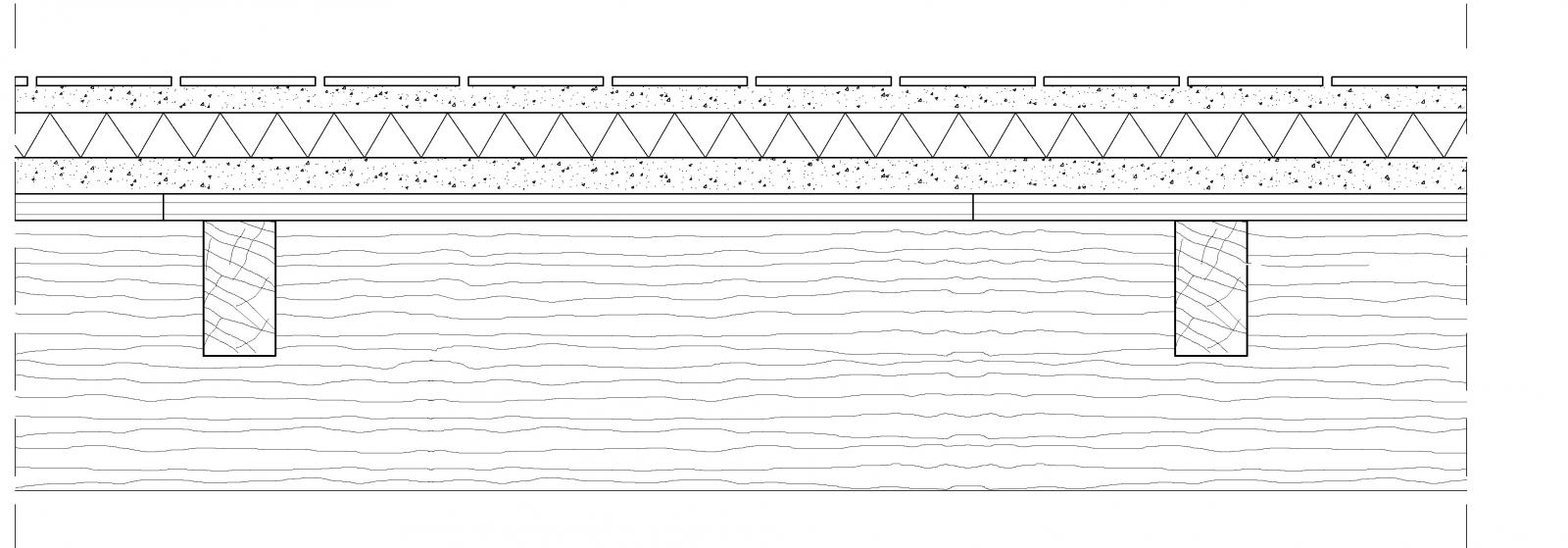
Progetto dei travetti di interasse 1m e luce 2.2m
Calcolo dei carichi per i travetti
Qs = 0,21 KN/mq Carico Strutturale
Assito in legno (s = 0.035) P = V x g = Volume x Peso specifico = (1m x 1m x 0,035m) calcolato per un’area di 1m x 1m) x 6KN/mc
Qa = 2KN/mq Sovraccarico accidentale per una civile abitazione
Qp = 1,73KN/mq Carico permanente non strutturale
Pavimento in gres porcellanato (s = 0,01)= 20KN/mc = 0,2KN/mq
Massetto (cls con calcarenite) (s =0,03) = 20KN/mc = 0,6KN/mq
Isolante termo-acustico (s= 0,05) = 0,6KN/mc = 0,03 KN/mq
Caldana (s= 0,04) = 10KN/mc = 0,4KN/mc
Impianti 0,5KN/mq
Q tot= 0,21+2+1,73= 3,94KN/mq Carico totale al mq
A questo punto inserisco i valori dei 3 carichi nel foglio di calcolo excel e ottengo il valore del carico totale al metro lineare:
3,94KN/mq x 1m = 3,94KN/m
Con il carico al metro lineare e l’interasse, ottengo il momento massimo che per una trave doppiamente appoggiata è pari a ql^2/8; impostate poi la resistenza a snervamento fmk e il suo coefficiente moltiplicativo kmod, ottengo la tensione di progetto fd.
Adotto una base ragionevole pari a 8cm e ottengo l’altezza attraverso la formula:
h = (6 x M x 1000/(bfd ))^0,5
Verifica del travetto
Ottenute le dimensioni del travetto, aggiungo al carico strutturale quello dei travetti
(0,08m x 0,15m x 6KN/mc)/1m = 0,072KN/mq e verifico che dal punto di vista dimensionale la sezione sia corretta.
Q’s = 0,21+0,072= 0,282KN/mq
Momento = ql^2/8= (4,012 x 2,2 x 2,2)/8= 2,427KNm
h’= (6M/bfd )^0,5 = (6 x 2,43 x 1000/8 x 9,66)^0,5= 13.7cm il dimensionamento precedentemente eseguito è corretto Trave GH28 8x15
Progetto della trave di interasse 2,2m e luce 4,075m
Calcolo dei carichi per la trave
Qs = 0,282KN/mq Carico Strutturale
Assito in legno (s = 0.035) P = V x g = Volume x Peso specifico = (1m x 1m x 0,035 m) calcolato per un’area di 1m x 1m) x 6KN/mc -> 0,21 KN/mq
Travetti in legno (0,08m x 0,15m x 6KN/mc)/ 1m = 0,072KN/mq
Qa = 2KN/mq Sovraccarico accidentale per una civile abitazione
Qp = 1,73KN/mq Carico permanente non strutturale
Pavimento in gres porcellanato (s = 0,01)= 20KN/mc = 0,2KN/mq
Massetto (cls con calcarenite) (s =0,03) = 20KN/mc = 0,6KN/mq
Isolante termo-acustico (s= 0,05) = 0,6KN/mc = 0,03 KN/mq
Caldana (s= 0,04) = 10KN/mc = 0,4KN/mc
Impianti 0,5KN/mq
Q tot= 0,282+2+1,73= 4.012KN/mq
Come per i travetti, inserisco i valori dei 3 carichi nel foglio di calcolo excel e ottengo il valore del carico totale al metro lineare:
3,94KN/mq x 2,2m = 8,826KN/m
Con il carico al metro lineare e l’interasse, ottengo il momento massimo che per una trave doppiamente appoggiata è pari a ql^2/8; impostate poi la resistenza a snervamento fmk e il suo coefficiente moltiplicativo kmod, ottengo la tensione di progetto fd.
Adotto una base ragionevole pari a 15cm e ottengo l’altezza attraverso la formula:
h = (6 x M x 1000/(bfd ))^0,5
Verifica della trave
Ottenute le dimensioni della trave, aggiungo al carico strutturale quello della trave
(0,15m x 0,30m x 6KN/mc)/2,2m = 0,123KN/mq e verifico che dal punto di vista dimensionale la sezione sia corretta.
Q’s = 0,282+0,123= 0,405KN/mq
Momento = ql^2/8= (9,097 x 4,075 x 4,075)/8= 18,88KNm
h’= (6M/bfd )^0,5 = (6 x 18,88 x 1000/15 x 9,66)^0,5= 27,97cm il dimensionamento precedentemente eseguito è corretto Trave GH28 15x30cm
SOLAIO IN ACCIAIO
Anche per questo tipo di solaio i passi da eseguire sono i seguenti:
1)calcolo di tutti i carichi che gravano sulla trave (Qs, Qp e Qa)
2)calcolo delle dimensioni del travetto in acciaio a partire da un dato ipotizzato, la base e relativa verifica.
3)calcolo delle dimensioni della trave in acciaio a partire da un dato ipotizzato, la base e relativa verifica.
Progetto della Trave sull’allineamento B2-B3
Progetto dei travetti di interasse 1m e luce 2.2m
Qs = 1,65KN/mqCarico Strutturale
Lamiera grecata in acciaio A55/P600 h = 0,055m e s = 0,02 cm
Getto di completamento in cls armato h = 0,045 m
Qa = 2KN/mqSovraccarico accidentale per una civile abitazione
Qp = 1,43KN/m Carico permanente non strutturale
Pavimento in gres porcellanato (s = 0,01)= 20KN/mc = 0,2KN/mq
Massetto (cls con calcarenite) (s =0,03) = 20KN/mc = 0,6KN/mq
Isolante termo-acustico (s= 0,05) = 0,6KN/mc = 0,03 KN/mq
Pannello in cartongesso (s= 0,12) = 0,1KN/mq
Impianti 0,5KN/mq
Q tot= 1,65+2+0,2+0,6+0,03+0,1+0,5= 5,08KN/mq
A questo punto inserisco i valori dei 3 carichi nel foglio di calcolo excel e ottengo il valore del carico totale al metro lineare:
3,94KN/mq x 1m = 3,94KN/m
Con il carico al metro lineare e l’interasse, ottengo il momento massimo che per una trave doppiamente appoggiata è pari a ql^2/8.
Impostata la resistenza a snervamento fyk = 235N/mmq, ottengo la tensione di progetto
fd = 204,35N/mmqe il modulo di resistenza a flessione Wx = 15,04cm^3.
Scelgo un Wx = 20,03cm^3 a cui corrisponde una profilato
IPE80 b = 4,6cm h = 8cm P = 0,06KN/m.
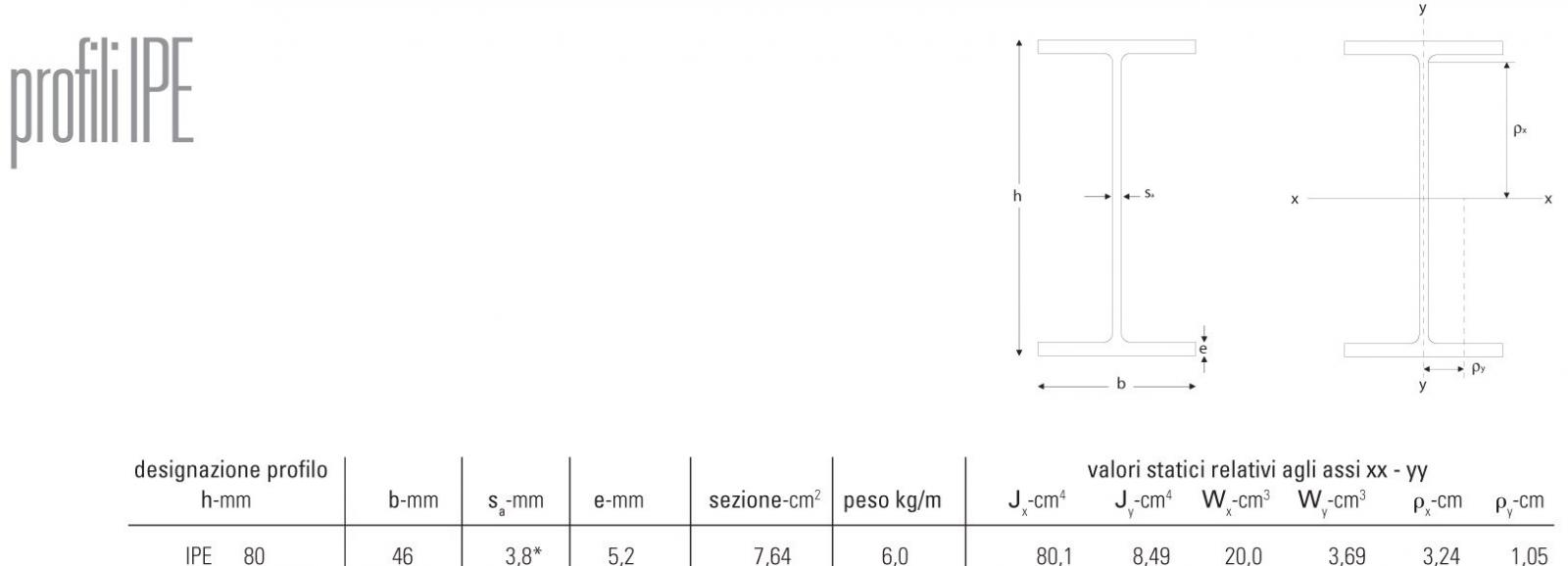
Verifica del travetto
Ottenute le dimensioni del travetto, aggiungo al carico strutturale quello del travetto 0,06KN/m/1m = 0,06KN/mq e verifico che dal punto di vista dimensionale la sezione sia corretta.
Q’s = 0,06+1,65=1,71KN/mq
Momento = ql^2/8= (5,14 x 2,2 x 2,2)/8= 3,109KNm
Con il nuovo valore di momento ottengo un modulo di resistenza a flessione
Wx = 15,22cm^3 che è minore del modulo di resistenza scelto Wx = 20,03cm^3 quindi la sezione è verificata.
Progetto della trave di interasse 2,2m e luce 4,075m
Q’s = 1,71KN/mqCarico Strutturale
Lamiera grecata in acciaio A55/P600 h = 0,055m e s = 0,02 cm
Getto di completamento in cls armato h = 0,045 m
Trave IPE80 0,06KN/m2
Qa = 2KN/mqSovraccarico accidentale per una civile abitazione
Qp = 1,43KN/mCarico permanente non strutturale
Pavimento in gres porcellanato (s = 0,01)= 20KN/mc = 0,2KN/mq
Massetto (cls con calcarenite) (s =0,03) = 20KN/mc = 0,6KN/mq
Isolante termo-acustico (s= 0,05) = 0,6KN/mc = 0,03 KN/mq
Pannello in cartongesso (s= 0,12) = 0,1KN/mq
Impianti 0,5KN/mq
Q tot= 1,71+2+0,2+0,6+0,03+0,1+0,5= 5,14KN/mq
A questo punto inserisco i valori dei 3 carichi nel foglio di calcolo excel e ottengo il valore del carico totale al metro lineare:
5,14KN/mq x 2,2m = 11,308KN/m.
Con il carico al metro lineare e l’interasse, ottengo il momento massimo che per una trave doppiamente appoggiata è pari a ql^2/8.
Impostata la resistenza a snervamento fyk = 235N/mmq, ottengo la tensione di progetto
fd = 204,35N/mmqe il modulo di resistenza a flessione Wx = 114,86cm^3. Scelgo un
Wx = 146,3cm^3 a cui corrisponde una profilato
IPE180 b = 9,1cm h = 18cm P = 0,188KN/m.
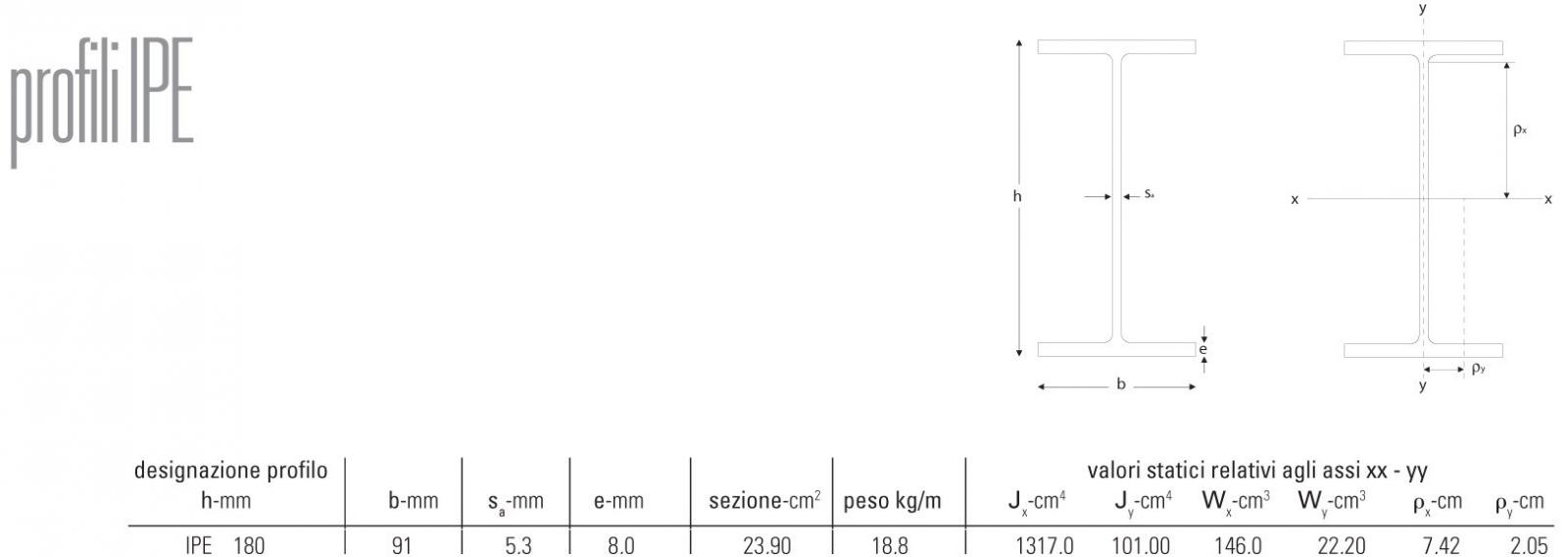
Verifica della trave
Ottenute le dimensioni della trave, aggiungo al carico strutturale quello della trave 0,188KN/m/2,2m = 0,085KN/mq e verifico che dal punto di vista dimensionale la sezione sia corretta.
Q’s = 0,085+1,71=1,795KN/mq
Momento = ql^2/8= (11,495 x 4,075 x 4,075)/8= 23,86KNm
Con il nuovo valore di momento ottengo un modulo di resistenza a flessione Wx = 116,76cm^3 che è minore del modulo di resistenza scelto
Wx = 146,3cm^3 quindi la sezione è verificata.
SOLAIO IN CLS
Per questo tipo di solaio i passi da eseguire sono i seguenti:
1)calcolo di tutti i carichi che gravano sulla trave (Qs, Qp e Qa)
2)calcolo delle dimensioni della trave in cls armato a partire dal solaio e relativa verifica.
Progetto della Trave sull’allineamento B2-B3
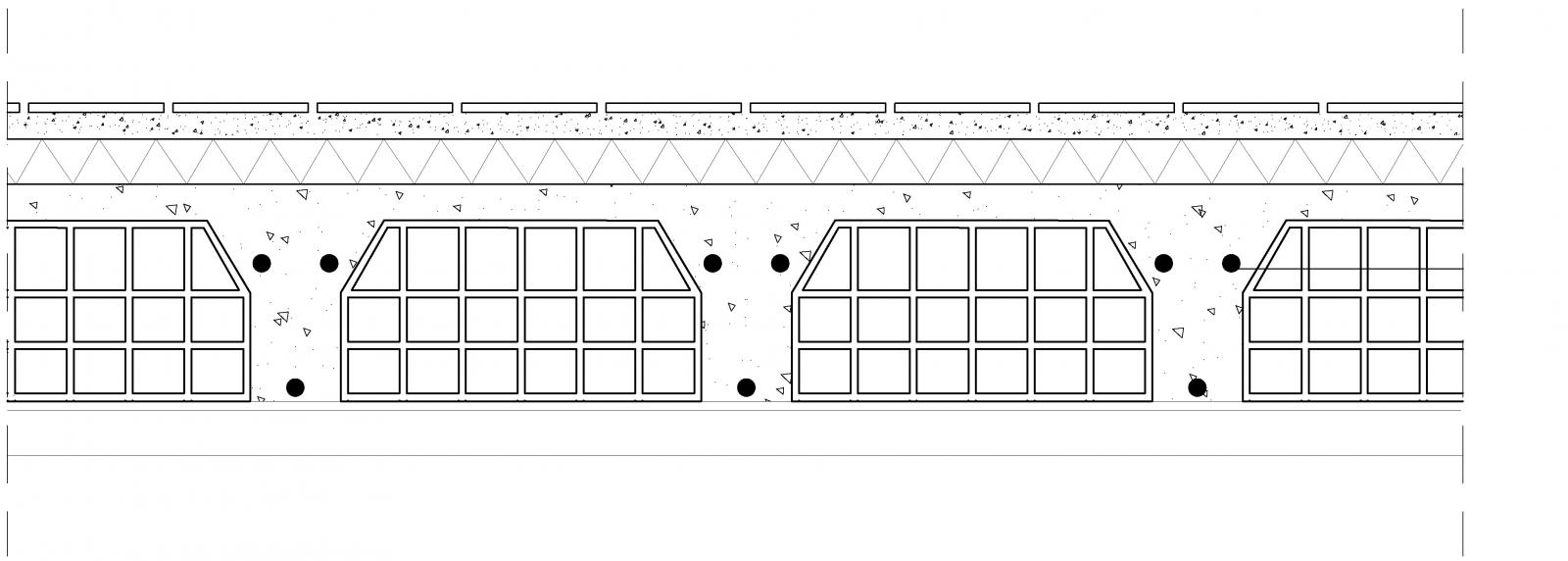
Imges impalcato e particolare
Progetto della trave di interasse 2,2m e luce 4,075m
Qs = 2,66KN/mq
Getto di completamento in cls armato h = 0,04 m
Pignatta h = 0,2 m l = 0.4 m
Travetti in acciaio l = 0.1 m
Qp = 1,43KN/mCarico permanente non strutturale
Pavimento in gres porcellanato (s = 0,01)= 20KN/mc = 0,2KN/mq
Massetto (cls con calcarenite) (s =0,03) = 20KN/mc = 0,6KN/mq
Isolante termo-acustico (s= 0,05) = 0,6KN/mc = 0,03 KN/mq
Pannello in cartongesso (s= 0,12) = 0,1KN/mq
Impianti 0,5KN/mq
Q tot= 2,66+2+0,2+0,6+0,03+0,1+0,5= 6,09KN/mq
A questo punto inserisco i valori dei 3 carichi nel foglio di calcolo excel e ottengo il valore del carico totale al metro lineare:
6,09KN/mq x 2,2m = 13,398KN/m.
Con il carico al metro lineare e l’interasse, ottengo il momento massimo che per una trave doppiamente appoggiata è pari a ql^2/8.
Impostata la resistenza a snervamento fyk = 235N/mmq e la classe del cls C40/50, ottengo la tensione di progetto dell’acciaio fyd = 391,3N/mmq e del cls fcd = 22,86N/mmq.
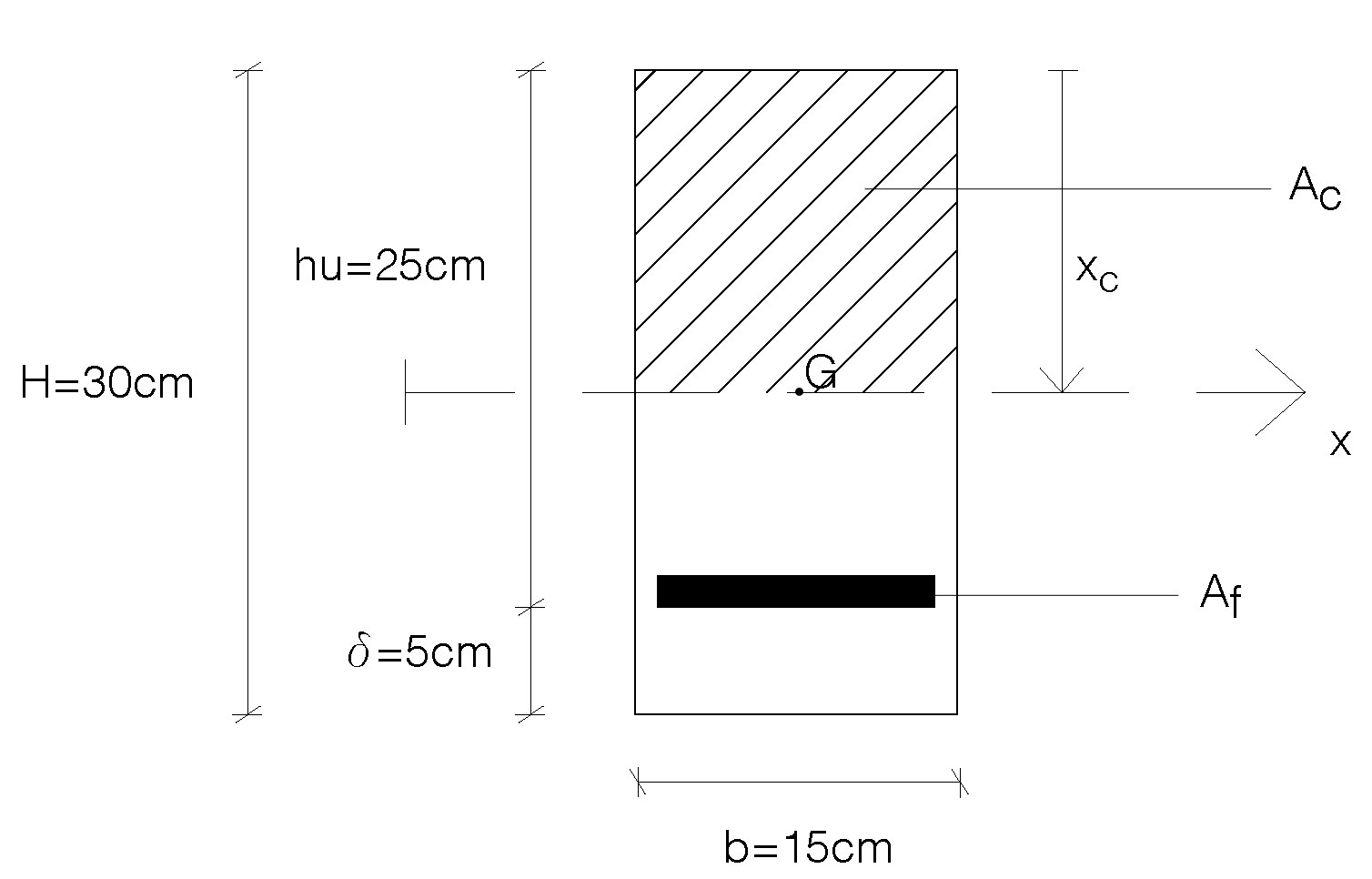
Ipotizzata una base ragionevole b = 15cm, ottengo un h utile = 20,28cm dalla formula
h = r(Mx1000/(fcd xb))^0,5. Dall’altezza che mi occorre non è quella utile ma quella della trave che è la somma dell’altezza utile più il copriferro (non resiste alla flessione ma è importantissimo perché ci “avverte” attraverso la fessurazione, del raggiungimento da parte della trave del collasso):
H = h utile + delta. Essendo il copriferro pari a 5cm e avendo ottenuto un H = 25,28cm, adotto un H = 30cm perché comunemente le altezze delle travi hanno valori interi che possono incrementare solo di un valore di 5 in 5cm.
Verifica della trave
Ottenute le dimensioni della trave, aggiungo al carico strutturale quello della trave (0,15m x 0,30m x 25KN/mc)/2,2m = 0,51KN/mq e verifico che dal punto di vista dimensionale la sezione sia corretta.
Q’s = 2,66+0,51= 3,17KN/mq
Momento = ql^2/8= (30,14 x 4,075 x 4,075)/8= 62,56KNm
h’ utile = r(Mx1000/(fcd xb))^0,5 = 2,25 (62,56 x 1000/(22,86 x15) = 21,12cm.
H’ = h utile + delta = 21,12 + 5= 26,12 cm quindi il dimensionamento precedentemente eseguito è corretto. Trave in cls C40/50 15x30cm
Esercitazione 3
Travatura reticolare spaziale
Disegno e analisi su SAP
L’argomento di questa esercitazione è il progetto di una travatura reticolare spaziale, di 4 moduli ripetuti per 6 file adottando un modulo di base di 2x2x2m, disegnata prima su Autocad e poi importata su SAP 2000. Prima di eseguire il disegno della struttura sono state impostate l’unità di misura in metri e le coordinate x,y,z nell’origine, per esportare con più facilità il file su SAP.
Con il comando polilinea disegniamo una trave a C con un’asta diagonale al suo interno, che rappresenta il modulo base da dover replicare per ottenere quello più complesso della travatura reticolare spaziale.
Tenendo premuti shift e la rotella del mouse passiamo alla vista 3D che ci mostra il nostro disegno “schiacciato” lungo la pianta, il piano xy. Volendo riprodurre la struttura in 3D, quindi disporre in verticale il nostro modulo, usiamo il comando ruota 3D e digitiamo l’asse x che corrisponde all’asse di rotazione e poi clicchiamo sull’asse y che corrisponde all’asse da ruotare.
Una volta ruotato il disegno, lo selezioniamo e adottando il comando serie lo riproduciamo 4 volte (righe = 1, colonne = 4, distanza 2m) lungo l’asse x che è l’asse lungo il quale ci interessa eseguire la serie. Quadruplicato il modulo, chiudiamo con una linea l’ultimo perché come detto prima, il modulo base è una C con un linea diagonale.
Adesso disegniamo la stessa struttura in direzione y ricordandoci di non duplicare le aste verticali già disegnate per la prima serie. Con il comando serie quadruplichiamo anche queste aste ottenendo una “parvenza” di travatura reticolare spaziale. Completiamo questa prima fila inserendo anche le diagonali per i correnti superiori e inferiori aiutandoci con il comando orbita (shift e tasto sinistro del mouse).
Ora che la prima fila è completata possiamo replicarla in serie ma dobbiamo ricordarci di cambiare l’UCS collocando l’asse x al posto dell’asse y così da facilitare il lavoro (UCS -> 3p e selezioniamo le direzioni che vogliamo assegnare agli assi x,y,z). Riproduciamo 7 volte la riga dei 4 moduli precedentemente creati con il comando serie (righe = 1, colonne = 7, distanza 2m) perché anche se la nostra struttura è composta da 4 moduli x 6 file è più semplice una volta eseguita la serie rimuovere linee aggiuntive piuttosto che aggiungerle.
Disegnata la struttura, il modello è stato esportato nel formato .dxf per poter esser letto dal software di calcolo SAP.
Una volta importato il modello, sono stati assegnati i vincoli agli estremi della struttura, 4 cerniere che costituiscono gli appoggi (seleziono il nodo -> assign -> joint -> restraints -> translation 1 e 2 che indicano l’impedimento delle traslazioni verticale e orizzontale), mentre per tutti gli altri nodi sono state selezionate le aste e sono state spuntate le caselle che indicano il rilascio dei momenti flettente e torcente quindi sono state inserite cerniere sferiche, perché operiamo in 3D (assign -> frame -> releases/partial fixity -> moment 22, moment 33 start e end che indicano l’inizio e la fine dell’asta).
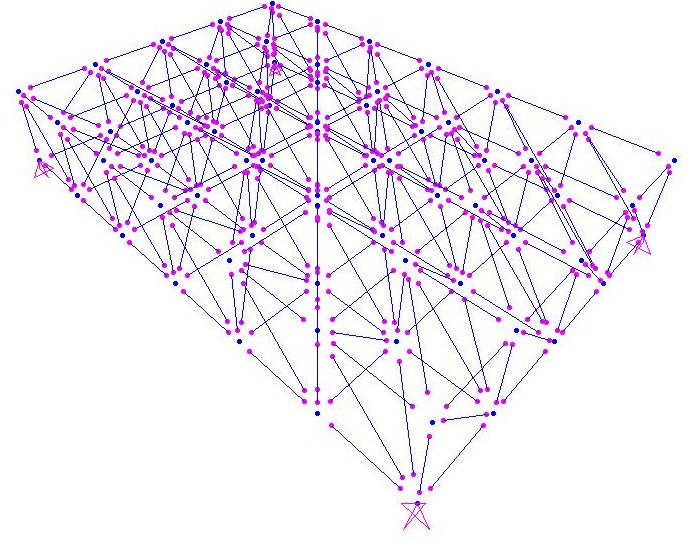
A questo punto abbiamo definito il materiale di cui sono composte le aste, l’acciaio (define -> materials -> add new material ->acciaio) e dopo averle selezionate lo abbiamo assegnato (assign -> frame -> frame sections -> add new property -> pipe (profilo cavo circolare) -> materiale acciaio).
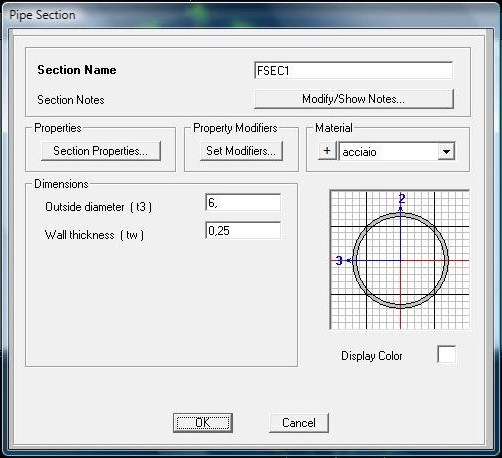
Infine attraverso la vista 2D dall’alto, piano xy, abbiamo selezionato i nodi ma solo dopo aver scrupolosamente spuntato la casella che rende invisibili le aste per poter assegnare facilmente i carichi che gravano sulla struttura (set display options -> frame/cables/tendons -> frames not in view).
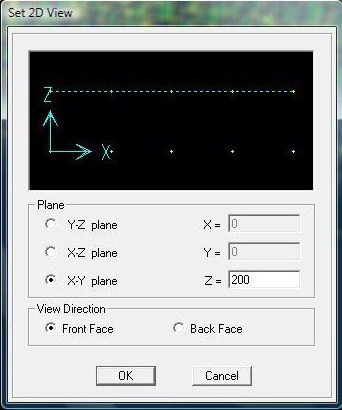
N.B.Non basta semplicemente selezionare i nodi dalla vista xy ma bisognare imporre a SAP che i carichi vengano assegnati sui nodi superiori quindi sempre con i nodi selezionati (view -> set 2D view -> plane xy -> z=2 perché 2 è l’altezza della travatura reticolare spaziale).
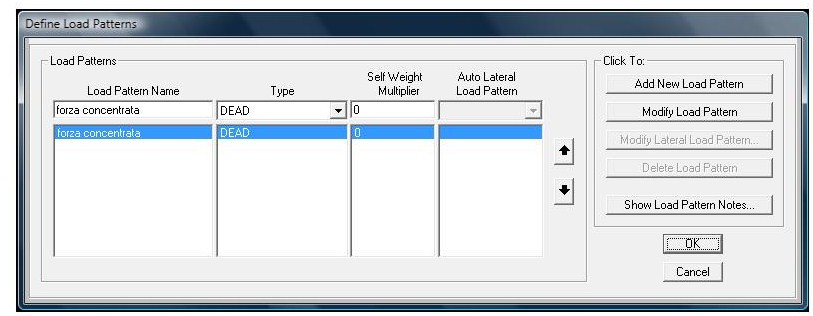
Definiamo quindi il carico con il nome di forza concentrata (define -> load patterns -> add new load pattern -> forza concentrata -> dead -> self weight multiplie = 0 perché non vogliamo che nell’analisi venga considerato il peso proprio).
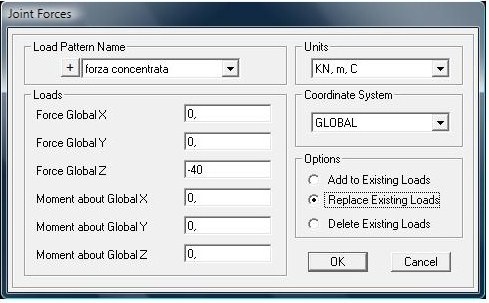
Selezionati i nodi, assegniamo il carico F = -40KN sull’asse z, asse ortogonale alla travatura e negativo perché rivolto verso il basso come una forza gravitazionale (assign -> joint loads -> forces -> load pattern name = forza concentrata -> force global z = -40KN).
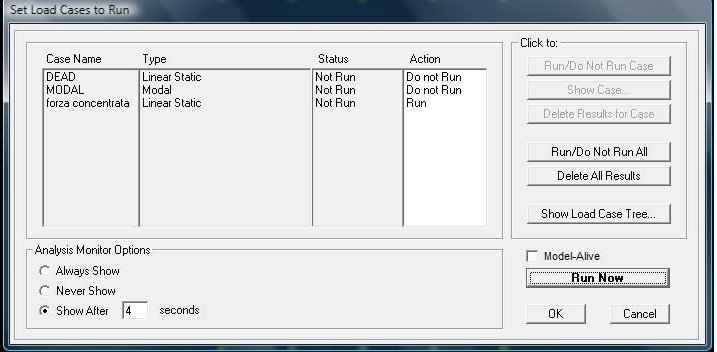
Ora che sono stati assegnati anche i carichi possiamo lanciare l’analisi ricordandoci però di limitarla alle sole forze concentrate che abbiamo collocato sulla struttura e non agli altri carichi che compaiono nella tabella (run analysis -> modal e dead -> do not run case -> forza concentrata -> run case -> run now).
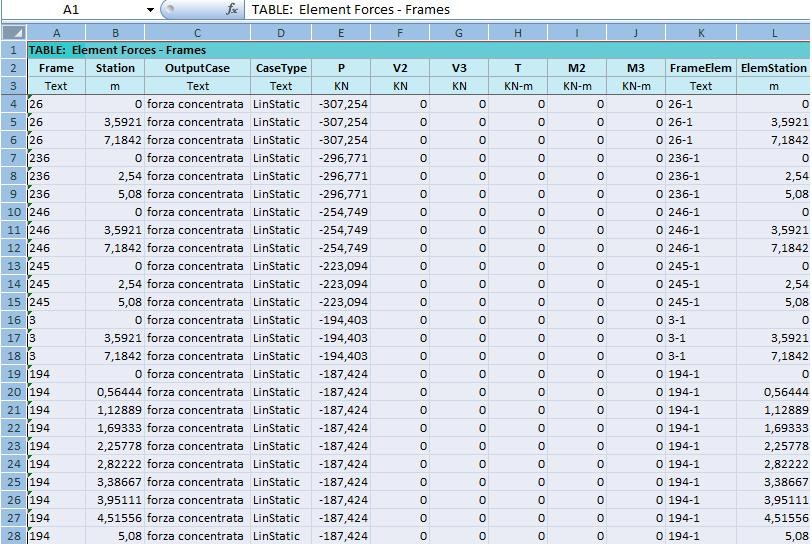
Sempre su SAP è possibile ricavare la tabella formato Excel che raffigura gli sforzi assiali che gravano su ogni singola asta (display -> show tables -> analysis results -> element output -> file -> export current table -> to excel).
N.B.= questo è possibile farlo solo dopo aver lanciato l’analisi e aver spuntato il comando che permette di visualizzare gli sforzi assiali sulle aste.
Di questi sforzi prenderemo in considerazione solamente i due valori massimi di trazione e compressione per eseguire il dimensionamento delle aste e farne le opportune verifiche a resistenza, snellezza e stabilità.
Per dimensionare l’asta di una struttura reticolare, si adotta la formula σ= N/A perché si considera semplicemente la tensione derivante dallo sforzo normale N che agisce su un’area A.
Dimensionamento dell’asta tesa e relativa verifica a resistenza.
In questo caso, per dimensionare l’asta tesa, è necessario prima calcolare l’area minima, A min e poi farne la verifica a resistenza. Adottando infatti un acciaio da carpenteria S275 quindi con un fyk = 275MPa (N/mmq), un gm₁=1,05 e tenendo in considerazione lo sforzo normale massimo di trazione ricavato dalla tabella excel di SAP, N = 258,93KN, otteniamo che A min = 258,93KN x 1000 x 1,05/275 N/mmq = 988 mmq = 9,9 cm².
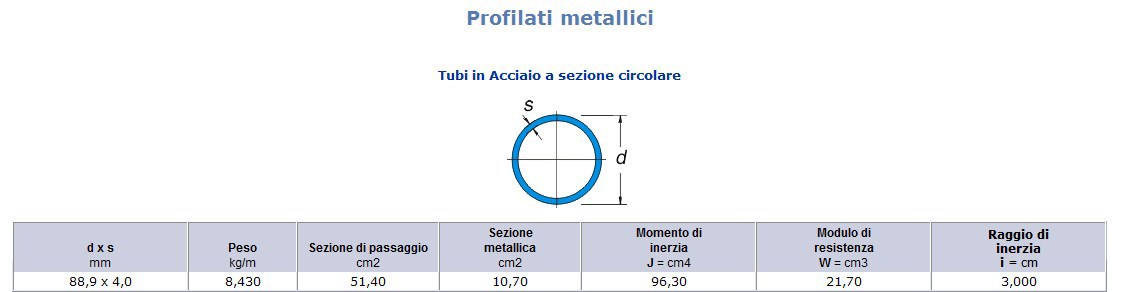
Consultando la tabella dei profili cavi a sezione circolare in acciaio, adottiamo quello la cui area è di poco maggiore al valore ottenuto dal calcolo per stare in sicurezza. Adotto un profilo con un dxs (diametro x spessore)= 88,9 x 4,0 mm A = 10,7 cm² Jx (momento d’inerzia) = 96,3 cm⁴ Wx (modulo di resistenza) = 21,7cm³ ρ (rho, raggio d’inerzia) = 3,0 cm.
A questo punto, dopo aver dimensionato l’asta tesa, ne eseguo la verifica a resistenza perché per l’acciaio teso l’unica verifica veramente significativa è quella a resistenza. Molto semplicemente si calcola la tensione di progetto fd e si verifica che questa sia minore/uguale alla tensione a snervamento dell’acciaio fyk. -> fd ≤fyk
fd = 258,93KN x 1000/10,7cm²x 100 = 241,99 MPa (N/mm²) -> 241,99MPa ≤ 275MPa -> asta verificata a resistenza.
Dimensionamento dell’asta compressa e relative verifiche a resistenza, snellezza e stabilità.
Per dimensionare correttamente l’asta compressa invece, non basta eseguire la verifica a resistenza perché essendo compressa è soggetta al carico di punta o meglio conosciuto come carico critico euleriano che provoca lo sbandamento dell’asta. Per ovviare allo sbandamento dovuto ad un valore elevato del rapporto h/l della trave, si stabilisce come è vincolata la trave e in base a quello si trova il P critico (carico critico).
Quindi oltre alla verifica a resistenza, vanno eseguite altre due verifiche, quella a snellezza e quella a stabilità. Per dimensionare l’asta compressa svolgiamo gli stessi passaggi di quella tesa perché se pur compressa, sempre di acciaio parliamo.
Adottiamo l’acciaio S275 quindi con un fyk = 275MPa (N/mmq), un gm₁=1,05 e teniamo in considerazione lo sforzo normale massimo di compressione ricavato dalla tabella excel di SAP, N = 307,25KN.
Dalla formula σ= N/A otteniamo che A min = 307,25KN x 1000 x 1,05/275 N/mmq = 1117 mmq = 11,17 cm².
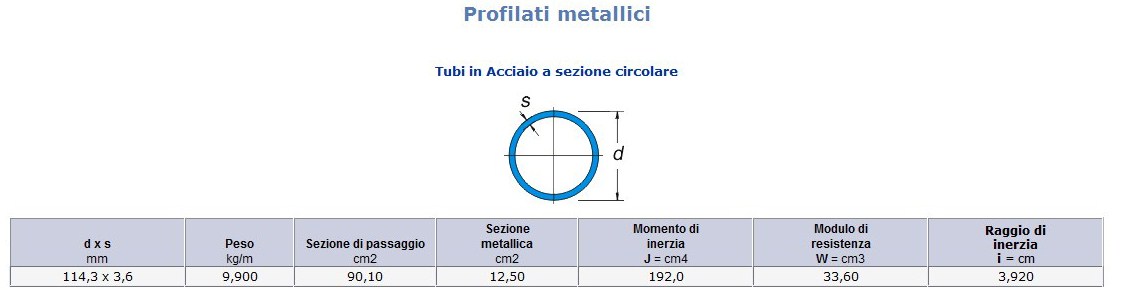
Consultando la tabella dei profili cavi a sezione circolare in acciaio, adottiamo quello la cui area è di poco maggiore al valore ottenuto dal calcolo per stare in sicurezza. Adotto un profilo con un dxs (diametro x spessore)= 114,3 x 3,6 mm A = 12,5 cm² Jx (momento d’inerzia) = 192 cm⁴ Wx (modulo di resistenza) = 33,6cm³ ρ (rho, raggio d’inerzia) = 3,92 cm.
Verifica a resistenza
fd ≤fyk
fd = 307,25KN x 1000/12,5cm²x 100 = 245,8 MPa (N/mm²) -> 245,8MPa ≤ 275MPa -> asta verificata a resistenza.
Verifica a snellezza
λ<200
λ= l₀/ρconl₀= βx l e ρ= raggio d’inerzia della sezione in esame
β= numero di semionde visibili per il tipo di vincolo in esame
Nel nostro caso, l’asta della travatura reticolare, va considerata come una trave doppiamente incernierata quindi la β = 1 e di conseguenza l₀= l. Il raggio d’inerzia lo desumiamo dalle tabelle ed è ρ= 3,92 cm. λ = 283 cm x 1 /3,92 cm = 72,2<200 -> asta verificata a snellezza.
Verifica a stabilità
Nd ≤Nbrd dove Nd è lo sforzo assiale che agisce sull’asta in esame mentre Nbrd è la resistenza all’instabilità per l’asta compressa ed è pari a Nbrd = χA fyk/gm₁. A loro volta χ = 1/Φ+(Φ²-⁻λ²)^0,5≤1 ;
⁻λ= (Afyk / Pcritico)^0,5 ;
Φ= 0,5[1+α (⁻λ– 0,2)+ ⁻λ²] e α è un coefficiente chiamato fattore di imperfezione ed è α=0,21
A sua volta, perché l’asta sia verificata,Nbrd<P critico dove P critico = p² E Jmin/l₀².
Eseguendo i calcoli ottengo che:
P critico = (3,14²x 210000N/mm²x 192 cm⁴ x 10000 / 283²cm x 10)/1000 = 496,4KN
⁻λ² = 12,5cm²x 100 x 275MPa/496,4 x 1000 = 0,69
Φ = 0,5[1+0,21(√0,69-0,2)+0,69] = 0,9
χ = 1/ 0,9+(0,9²-0,69²)^0,5 =0,68≤1
Nbrd = (0,68 x 12,5cm²x 100 x 275MPa/1,05)/1000 = 222,62KN
N.B. = il risultato ottenuto non è accettabile perchè Nd deve essere ≤Nbrd mentre invece in questo caso Nd = 307,25KN ≥222,62KN = Nbrd. Quindi bisogna adottare un’area maggiore, quindi un profilo più grande per garantire la verifica a stabilità.
Eseguiamo nuovamente i calcoli:
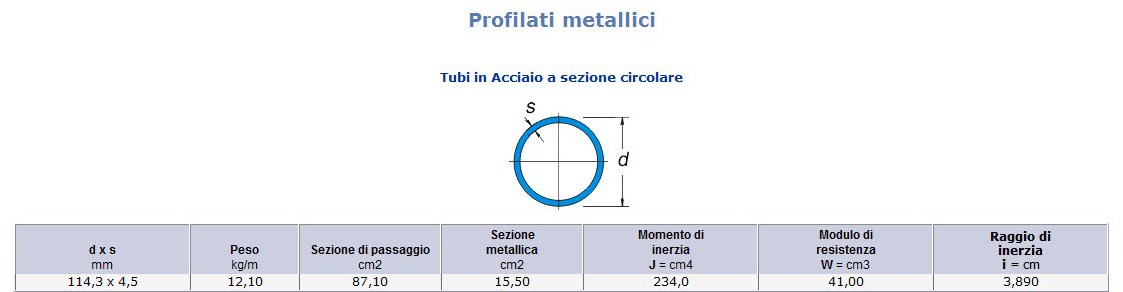
Consultando la tabella dei profili cavi a sezione circolare in acciaio, adottiamo quello la cui area è superiore al valore adottato precedentemente. Prendiamo quindi un profilo con un dxs (diametro x spessore)= 114,3 x 4,5 mm A = 15,5 cm² Jx (momento d’inerzia) = 234 cm⁴ Wx (modulo di resistenza) = 41cm³ ρ (rho, raggio d’inerzia) = 3,89 cm.
Verifica a resistenza
fd ≤fyk
fd = 307,25KN x 1000/15,5cm²x 100 = 198,225 MPa (N/mm²) -> 198,225MPa ≤ 275MPa -> asta verificata a resistenza.
Verifica a snellezza
λ<200
λ= l₀/ρ con l₀= βxl e ρ= raggio d’inerzia della sezione in esame
β= numero di semionde visibili per il tipo di vincolo in esame
quindi la β = 1 e di conseguenza l₀= l. Il raggio d’inerzia lo desumiamo dalle tabelle ed è
ρ= 3,89 cm. λ = 283 cm x 1 /3,89 cm = 72,75<200 -> asta verificata a snellezza.
Verifica a stabilità
Nd ≤Nbrd
P critico = (3,14²x 210000N/mm²x 234 cm⁴ x 10000 / 283²cm x 10)/1000 = 606,24KN
⁻λ² = 15,5cm²x 100 x 275MPa/604,95 x 1000 = 0,703
Φ = 0,5[1+0,21(√0,7-0,2)+0,7] = 0,9186
χ = 1/ 0,9168+(0,9168²-0,69²)^0,5 =0,769≤1
Nbrd = (0,769x 15,5cm²x 100 x 275MPa/1,05)/1000 = 312,2KN
Adesso anche la verifica a stabilità risulta corretta infatti Nd≤Nbrd ovvero 307,25KN≤312,2KN -> asta verificata a stabilità.
Esercitazione 4
Ripartizione delle forze sismiche (in collaborazione con Beatrice Nanni, Flavia Valdarnini, Sabrina Zhu)
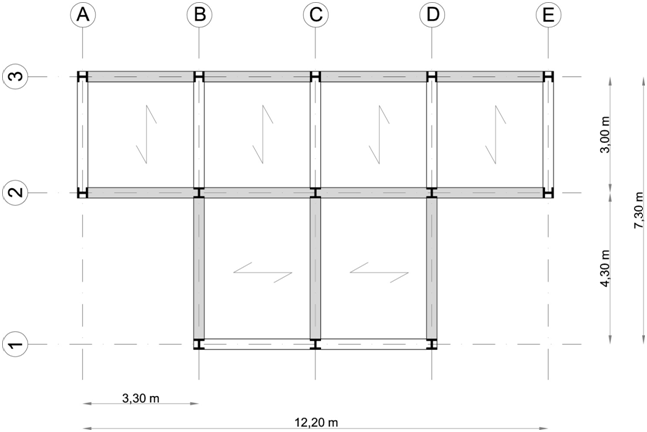
(le travi in grigio corrispondono alle travi portanti, ovvero quelle che portano tutti i carichi gravanti sul solaio)
L'impalcato in esame è una struttura a forma di T composta da 5 telai shear type in direzione verticale e 3 telai shear type in direzione orizzontale. Di questi telai, 5 sono i controventi determinati in base all’orditura del solaio.
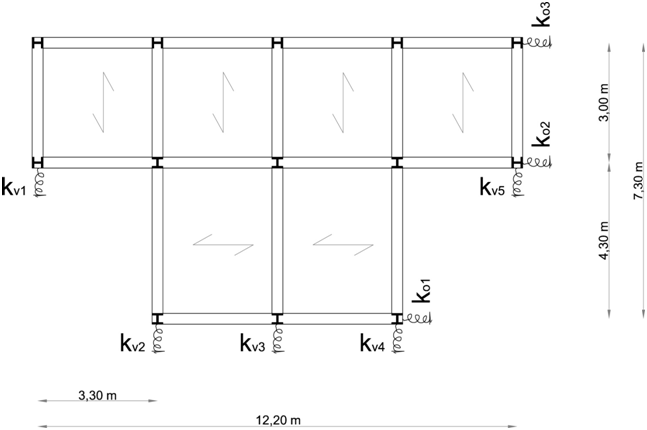
La struttura è 2 volte iperstatica quindi per risolvere il sistema è stato necessario definire il solaio come un corpo rigido piano (per il quale vale traslazione orizzontale, verticale e rotazione rigida attorno ad un punto) e introdurre vincoli elastici (molle) che si comportano secondo la legge di Hooke F= K δ. I pilastri sono stati posizionati in modo tale da avere il momento d’inerzia massimo nella direzione del momento flettente derivante dal carico del solaio.
Con il sussidio del foglio di calcolo excel, che permette un riscontro in termini numerici rapido e completo, è stato possibile analizzare lerigidezze dei controventi, il centro di massa, il centro delle rigidezze, l’analisi dei carichi sismici e la ripartizione del sisma lungo l’asse X e Y.
Rigidezze dei controventi
Primo Step
In questa tabella è stata calcolata la rigidezza di ogni singolo controvento attraverso la formula:
K = 12 EJ/H³dove E (modulo di Young, per l’acciaio 210000 MPa; per il cls 21000 MPa), J (momento d’inerzia, in direzione X = bh³/12 ; in direzione Y = hb³/12) e H (altezza del solaio interpiano pari a 4m).
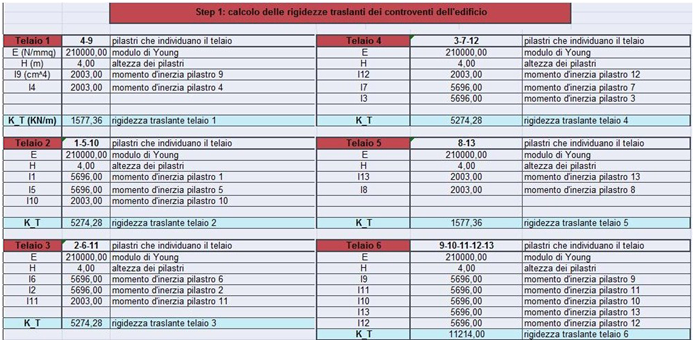
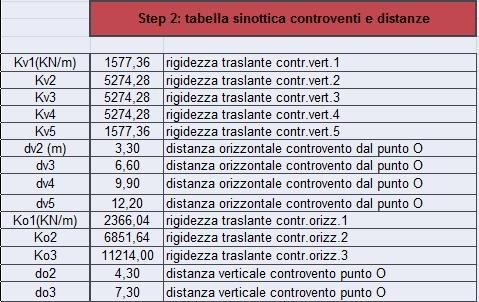
Secondo Step
Stabilite le rigidezze dei controventi sono state calcolate le distanze di questi da un punto fisso chiamato O (origine). Per il telaio verticale 4-9 e il telaio orizzontale 1-2-3 le distanze dall’origine sono pari a 0 in quanto i telai sono collocati sulla retta che congiunge con l’origine O.
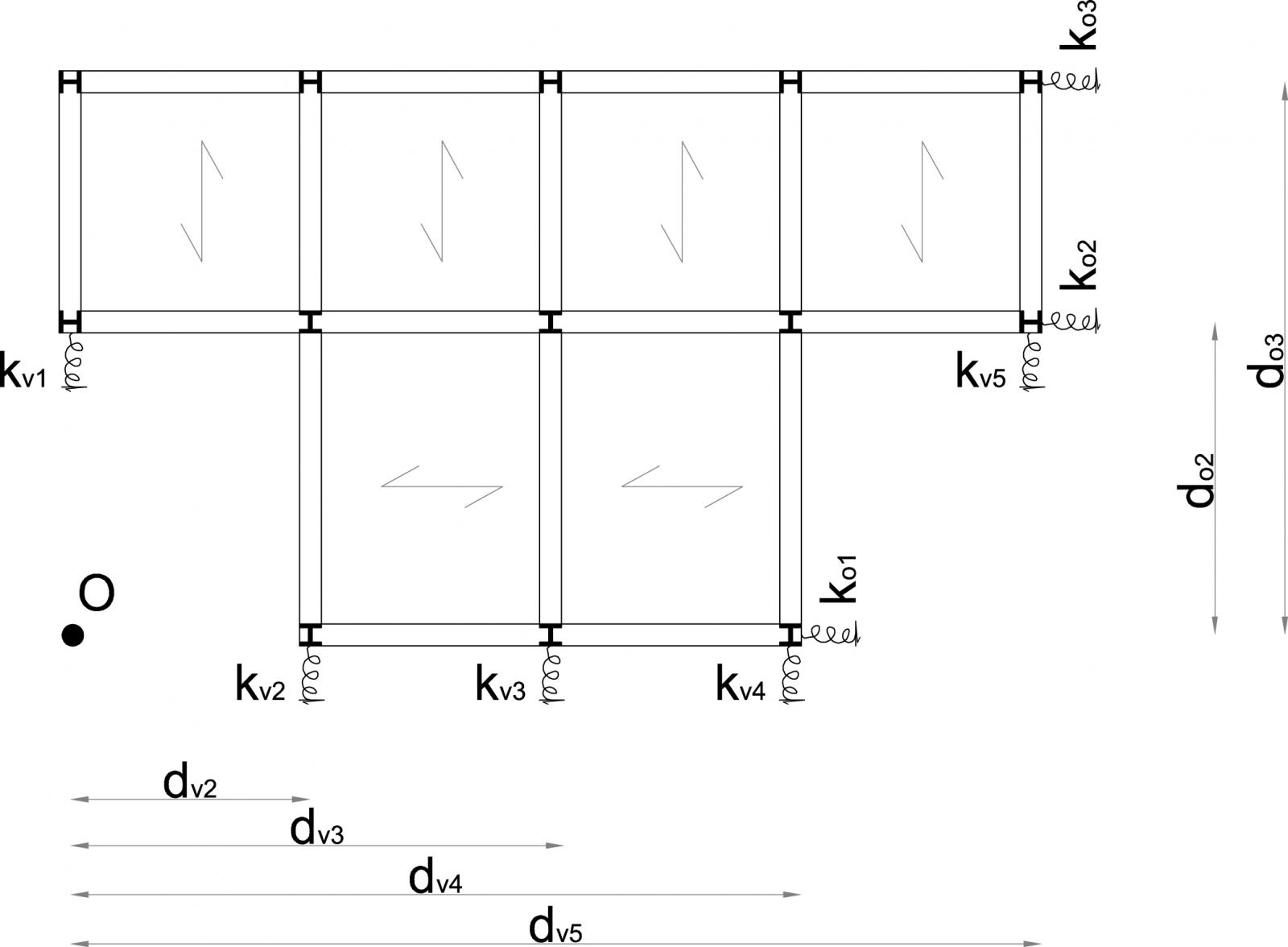
Centro di massa
Terzo Step
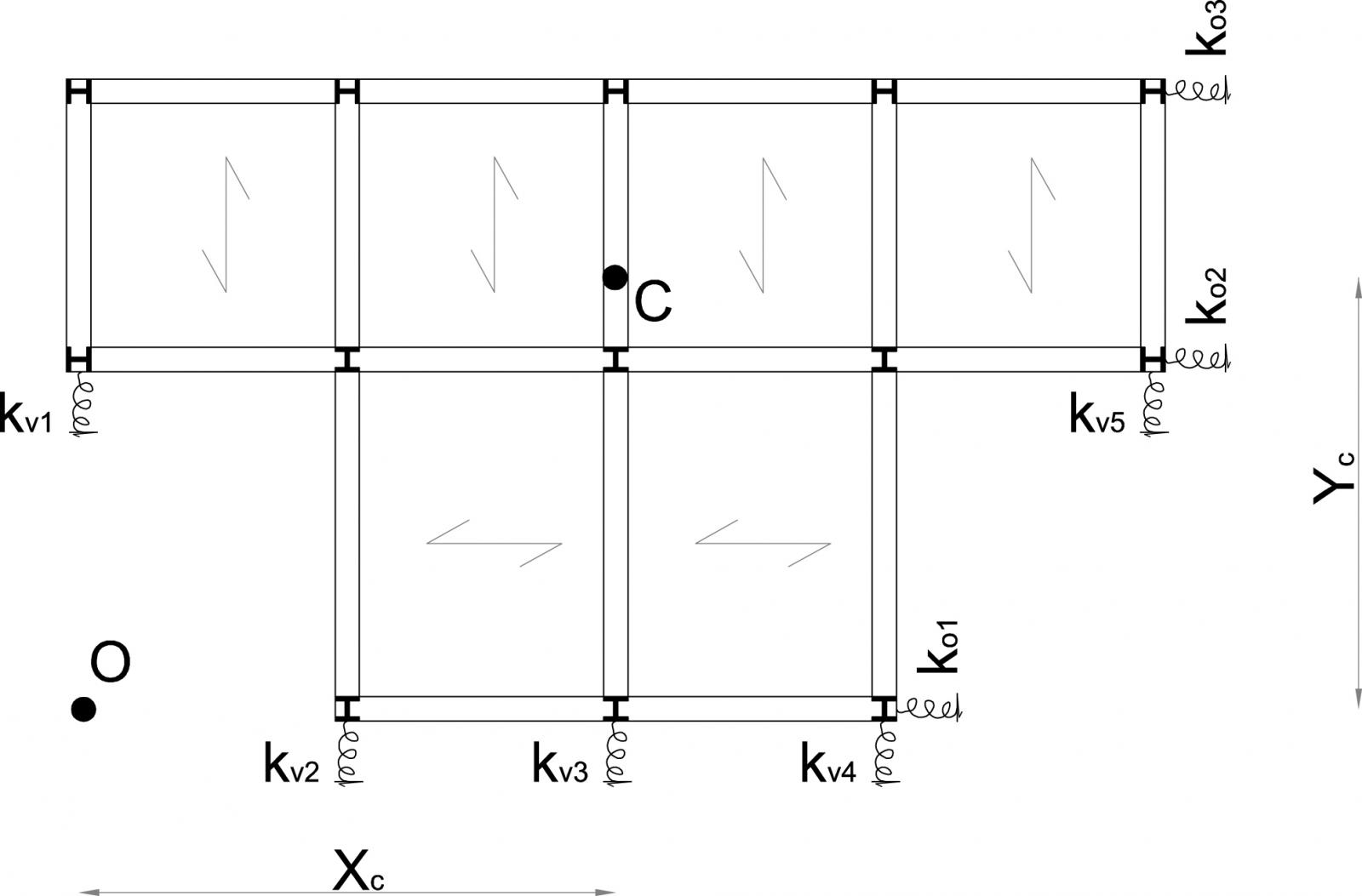
Una volta stabilite le rigidezze dei telai e le loro distanze dall’origine O, l’impalcato è stato suddiviso in due aree A1= 36,6m² e A2 = 28,38m² delle quali sono stati calcolati i centri di massa. Per determinare i centri di massa è stato preso come punto di riferimento l’origine O e sono state determinate le distanze (x_G1,y_ G1) e le distanze (x_ G2,y_ G2). Infine è stato calcolato il centro di massa dell’intera struttura secondo le sue coordinate
X_G: (A1x_G1)+(A2x_G2)/A1+A2= 6,60m
Y_G: (A1y_G1)+(A2y_G2)/A1+A2= 4,28m
Calcolo del centro di rigidezze e delle rigidezze globali
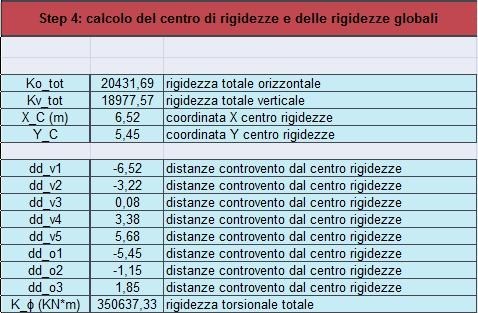
Quarto Step
Determinate tutte le rigidezze dei controventi (vedi Step 1) orizzontali e verticali, è stata calcolata la rigidezza totale traslante verticale e quella totale traslante orizzontale : Kvtot e Kotot. Dalle due rigidezze totali si è ottenuto il centro delle rigidezze in base alla formula:
X_C=(kv1 dv1)+(kv2 dv2)+(kv3 dv3)+(kv4 dv4)+(kv5 dv5)/kvtot = 6,52m
Y_C=(ko1 do1)+(ko2 do2)+(ko3 do3)/kotot = 5,45m
Una volta determinata la posizione del centro delle rigidezze, sono state invece determinate le distanze dei controventi verticali (ddv) e quelli orizzontali (ddo) dal centro delle rigidezze.
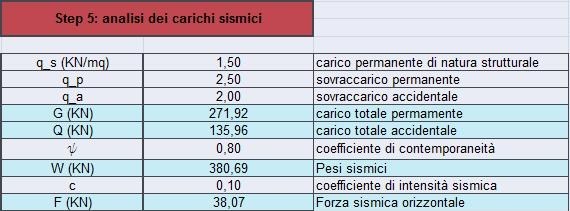
Analisi dei carichi sismici
Quinto Step Attraverso questa tabella è stata determinata la forza sismica che corrisponde al prodotto tra la massa dell’edificio per l’accelerazione che il corpo subisce per effetto del trascinamento (dato dalla Normativa in riferimento alla tipologia strutturale): F= ma dove a= cg, c <1 (coeff. di intensità sismica, più è alto maggiore è il sisma) e g (accelerazione gravitazionale).
F= mcg= c(mg)= cPdove P o W (forza peso) = G (sovraccarico tot. permanente (qs+qp)Atot) x Ψ (coefficiente di contemporaneità = 0.80) x Q (sovraccarico accidentale dato dalla destinazioned’uso dell’edificio).
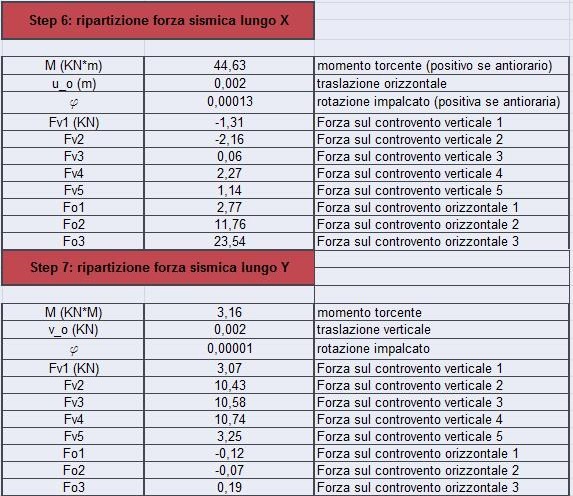
Ripartizione forza sismica lungo X e Y
Sesto e Settimo Step
Con questo step è stata studiata la ridistribuzione della forza sismica sui controventi orizzontali. Prima di stabilire la distribuzione della forza sui controventi, è stato necessario determinare il valore del momento torcente (rotazione dell’impalcato dovuta alla mancata coincidenza tra centro delle masse e centro delle rigidezze): Mt= Fxb dove F (Forza sismica) e b (distanza dal punto C (centro delle rigidezze) al punto G (centro delle masse)). Bisogna fare attenzione però perché essendo la forza sismica ripartita lungo X e Y, il braccio b cambia se si considera il Momento torcente lungo X o lungo Y. Infatti nel caso di X: b= (Y_C - Y_G); nel caso di Y: b= (X_C – X_G). Per determinare invece la traslazione orizzontale dell’impalcato la formula è: Uo= F/kotot mentre per quella verticale si ha: Vo= F/kvtot.
Commenti recenti