blog di SERENA.MARIUCCI

L'esercitazione consiste nell'analisi del telaio di un piano tipo dell'edificio progettato, nell'individuazione del centro di massa e del centro delle rigidezze. Per una buona progettazione il centro di massa e quello delle rigidezze devono essere più vicini possibile, in modo che sotto azione di forze orizzontali si evitino  rotazioni e traslazioni dell'impalcato. Il fine dell'esercitazione è quello di garantire una resistenza strutturale dell'impalcato sottoposto all'azione di una forza sismica.

La struttura utilizzata per il progetto è una travatura reticolare spaziale, quindi sono stati rappresentati soltanto gli elementi strutturali, quali travi e setti murari.

 

Per determinare la posizione del centro di massa suddivido la struttura in tre rettangoli e vado a definire le coordinate x e y di ogni area.

C1_ (9-24)                    A1_ 864

C2_(9-6)                      A2_216

C3_(7,5-21)                 A3_630

Xc= (A1 X1+A2 X2+A3 X3) / (A1+A2+A3) = 8,44

Yc=(A1 Y1+A2 Y2+A3 Y3) / (A1+A2+A3) = 20,62            

Quindi le coordinate del centro di massa saranno:           X= (8,44 - 20,62)

Disegno quindi il centro di massa come un punto sulla pianta strutturale.

Disegnato il centro di massa assegno a tutti gli elementi la condizione di nodo rigido, questo affinché non si verifichino spostamenti e rotazioni relative.
Per calcolare il peso proprio dell'impalcato eseguo l'analisi considerando soltanto il peso proprio e verificando i valori sulle tabelle.

 

        Dalla tabella ricavo il peso proprio sommando tutti i valori della voce F3.

Il peso proprio dell'impalcato risulta   Pp= 4438,202 KN

La normativa mi fornisce il coefficiente di sicurezza da applicare alla struttura che è pari al 20% del peso dell'impalcato e che varia a seconda della zona in cui viene studiato il progetto.

quindi: 4438,202 x 0,2= 887,64              

Definisco ora idue casi di carico Fx ed Fy, ovvero le due componenti della forza orizzontale che andrò ad applicare nelle due differenti direzioni sul centro di massa. Una volta assegnati i carichi avvio l'analisi senza considerare il peso proprio e verifico la posizione del centro delle rigidezze.

   COMPONENTE X_         

 

COMPONENTE Y_

Dall'analisi risulta che il centro delle rigidezza non è coincidente con quello di massa.

 

 

Per un corretto comportamento dell'impalcato bisegerà far coincidere i due punti, effettuando delle modifiche sulla posizione degli elementi strutturali.

Per il progetto della travatura reticolare ho costruito su SAP un modello con modulo di 2x2 ripetuto più volte sul modello. Per impedire il passaggio di momento all'interno della sezione ho inserito in tutti i nodi delle cerniere interne, ho impostato poi delle cerniere esterne che vanno ad indicare i punti di appoggio della mia travatura reticolare. Assegnata la sezione ho definito un caso di carico con delle forze concentrate nelle cerniere, per ricavare la forza concentrata ho tenuto conto di questi parametri:

numero piani:3

Peso per piano: 10 KN/mq

Mq: 96 mq

Peso piano: 96x5= 960 KN

da cui ricavo il peso totate: 2880 KN

La forza che andò ad applicare sarà divisa su tutti i nodi quindi :

F= 2880/35= 82 KN  

dove 35 corrisponde al numero di nodi.

Terminata l'assegnazione delle forze si può procedere con l'analisi dalla quale ricavo i valori dellosforzo assiate e, facendo attenzione che quelli corrispondenti a taglio e momenti siano nulli.

A questo punto esporto direttamente da sap una tabella excell che riassume tutti gli sforzi normali agenti sulle diverse aste.

 

Utilizzo Tabelle di profilati metallici a sezione circolare, che è quella che ho impostato inizialmente su sap.

ASTE COMPRESSE

Ho effettuato il dimensionamento delle aste compresse prendendo in esame le più sollecitate.

In questo caso prendiamo in considerazione alcuni fattori, come la lunghezza dell'asta (l), il modulo di elasticità (E), resistenza di design(f_yd)e la tipologia del vincolo (β) , in quanto per le aste compresse dobbiamo calcolare il modulo di inerzia minima (Imin), l'area minima (Amin), ed il raggio di inerzia (ρ_min), ed inoltre verificare che la snellezza (λ) non dovrà superare il valore 200. 

ASTE TESE

Anche in questo caso ho preso in considerazione le aste più sollecitate, che sono quelle che riportano il valore positivo dall'analisi sap.

una volta trovati i profili per le sezioni si procede all'analisi su sap, inserendo il profilato corretto.

 

 

 

L'esercitazione prevede il dimensionamento della trave più sollecitata nelle differenti tipologie: acciaio, cemento armato e legno. Nel seguente schema di carpenteria la trave più sollecitata risulta quella comresa tra i pilastri B2 e B3.

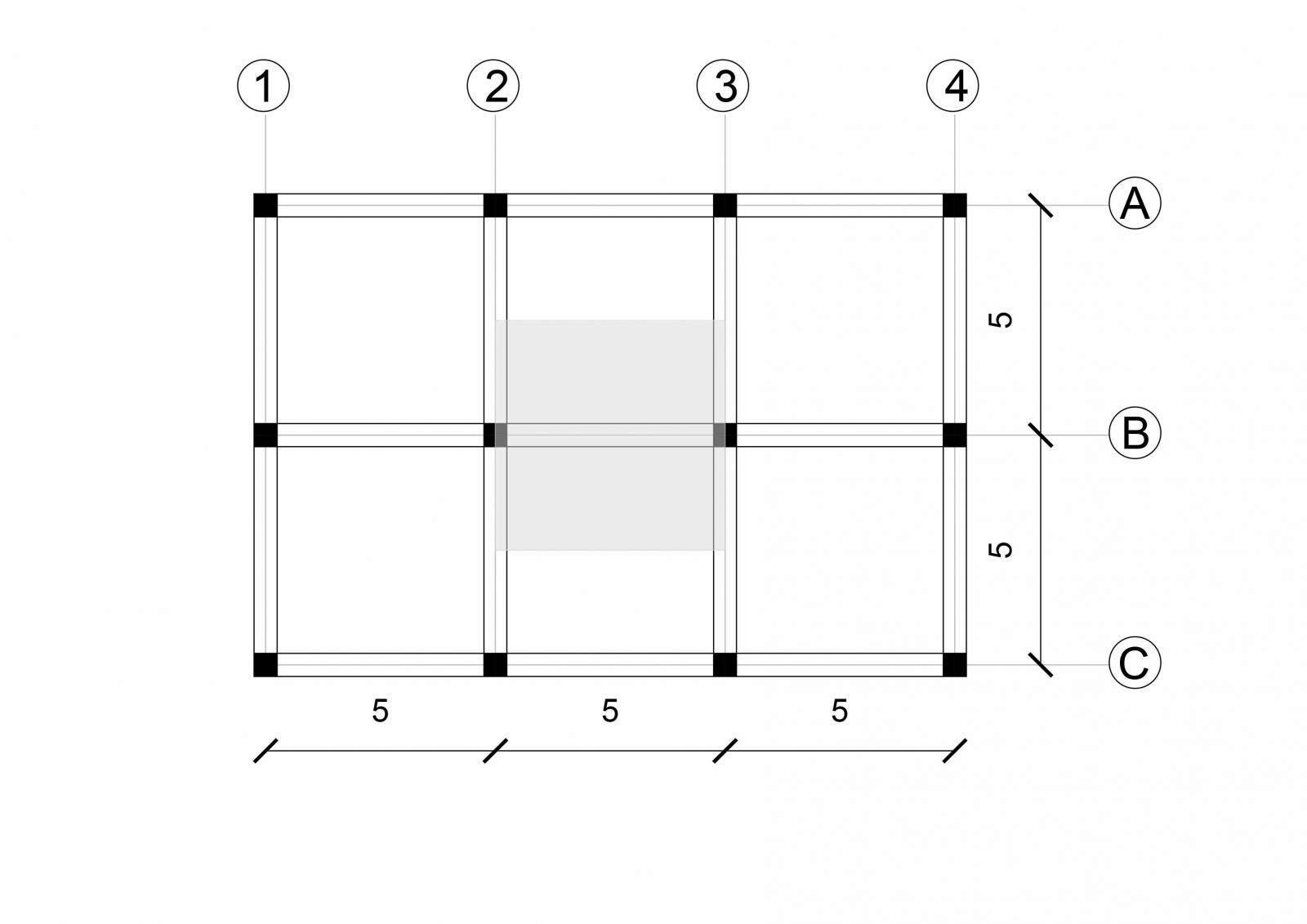
Luce della trave- 5 m

Interasse- 5 m

Area di influenza- 25 mq

Come prima cosa dobbiamo determinare tutti i carichi agenti sul solaio:

- Qs- carico strutturale, dovuto al peso propsio di tutti gli elementi strutturali.

- Qp-carico permanente, è il carico dovuto al peso proprio di tutti gli elementi che  gravano sul solaio e che non hanno funzione strutturale.

- Qa- carico accidentale, carico definito dalla normativa, che dipende dalla destinazione dìuso dell'edificio.

Una volta determinati i diversi tipi di carico, li vado a moltiplicare per dei coefficienti presi dalla normativa, quindi:

                Qtot= 1,3 x Qs+ 1,5 x Qp + 1,5 x Qa = KN/m^2

Per poter ricavare il carico che agisce direttamente sulla trave moltiplico il Qtot per l'interasse, ricavando così un Qu.

Essendo una trave doppiamente appoggiata il nostro Mmax= (Qu x l^2)/8

A questo punto vado a ricavare tutti i valori necessari per le diverse tipologie.

 

SOLAIO IN ACCIAIO:

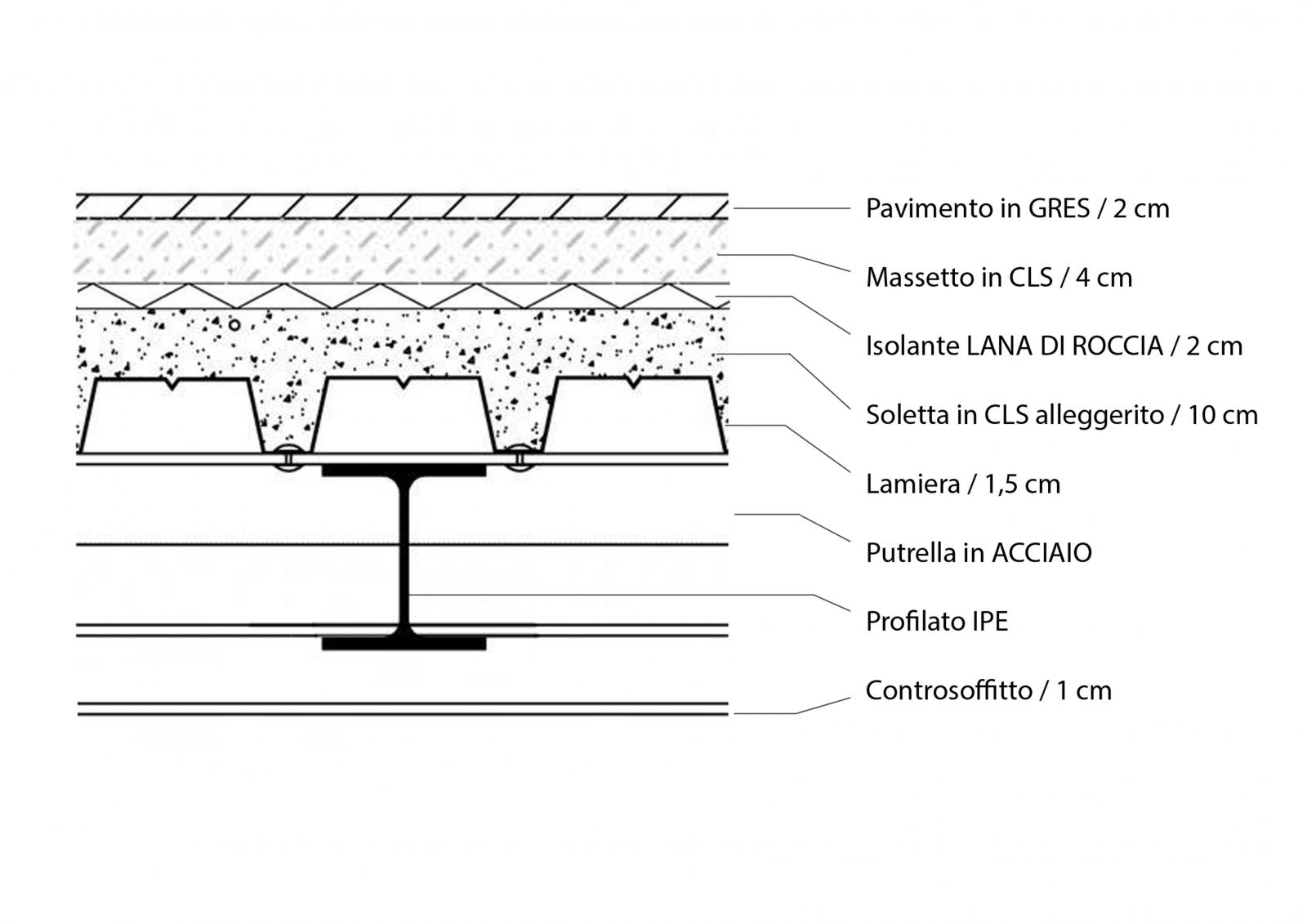
Carico strutturale (Qs)

- Soletta: S=100mm  ý=1500 Kg/mc

     pp: 0,1x1,5 =1,5 KN/mq

- Lamiera grecata: S=1,5mm    ý=7860 Kg/mc

   pp: 0,015x7,860= 0,119 KN/mq

  Qs= 1,6179 KN/mq

Sovraccarico Permanente (Qp)

- Pavimentazione: S=0,02m  ý=0,40 KN/mq

    pp: 0,02x0,4=0,008 KN/mq

- Massetto: S=0,4 m   ý=2100Kg/mc

   pp: 0,04x21=0,84 KN/mq

- Isolante Lana di roccia:  S=0,02m  ý=30 Kg/mc

     pp: 0,02x0,3=0,006KN/mq

- Controsoffitto:  S=0,01 m   ý= 1325 Kg/mc

     pp: 0,01x13,25=0,1325KN/mq

- Incidenza impianti= 0,5 KN/mq

- Incidenza tranmezzi= 1,00 KN/mq

Qp= 2,486 KN/mq

Sovraccarico accidentale (Qa)

Qa= 2KN/mq

Qu= 1,3 x Qs+ 1,5 x Qp + 1,5 x Qa =44,161 KN/mq

Il processo è stato eseguito utilizzando un foglio excell dal quale è stato possibile calcolare il valore del Mmax agente sulla trave e il Wxmin della sezione con il quale è stato scelto un profilato, in questo caso una IPE 330. Nella seconda riga excell aggiungo al valore di Qs il peso della trave IPE 330 diviso per l'interasse, quindi:

Qs: (1,6179+0,49)/ i= 1,7159 KN/mq

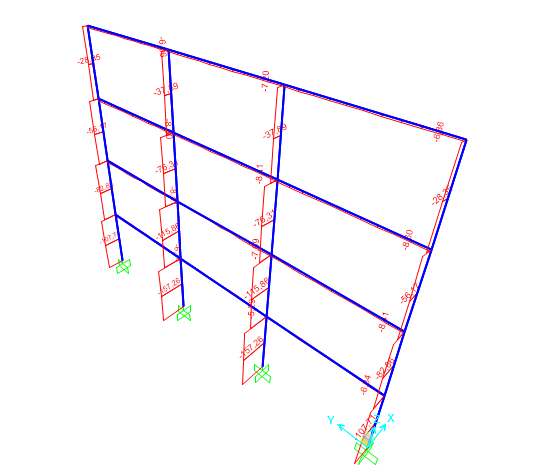
Utilizzando SAP abbiamo poi verificato che Mmax dato dal programma fosse veramente inferiore, nel mio caso ho ottenuto un valore di:

Mmax = 53 KN*m

che, rispetto al momento utilizzata in excell risulta verificata.

 

PILASTRO 

Il dimensionamento è stato eseguito anche per il pilastro più sollecitato, trovato lo sforzo normale, sono stati calcolati tutti i parametri necessari a definire la sezione, ho ricavato il momento di inerzia minimo ed ho cercato sul profilario una sezione con I>Imin. In base a questi dati è stato scelto un profilo HEB 240.

 

 

 

 

SOLAIO IN CALCESTRUZZO ARMATO

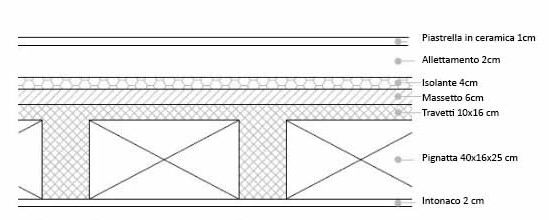
Sovraccarico strutturale (Qs)

- Soletta : S= 40mm    ý= 25,00 KN/mc

   pp: 25x0,04=1 KN/mq

- Travetti : S=20 mm     ý= 25,00 KN/mc

  pp: (0,16x0,1x1)x 25KN/mc= 0,4 x 2= =,8 KN/mq

- Pignatte: ý=8,00 Kg

  pp: 2x8= 16Kg = 0,16KN 

Qs= 1,96 KN/mq

 

Sovraccarico Permanente (Qp)

- Piastrelle: S=0,01m  ý=0,2 KN/mq

  pp: 0,01x0,2= 0,002 KN/mq

- Malta: S=0,02 m    ý=20 KN/mq

  pp: 0,02x20= 0,4 KN/mq

- Massetto: S= 0,06m   ý=25,00 KN/mc

    pp:25x0,06= 1,5 KN/mq

-Intonaco: S=0,02 m    ý=16 KN/mc

     pp: 0,02x16= 0,32 KN/mq

 

Incidenza tramezzi= 1,00 KN/mq

Incidenza impianti= 0,5 KN/mq

Qp= 3,762 KN/mq

 

Sovraccarico accidentale (Qa)

Qa= 2 KN/mq

 

Qu= 1,3 x Qs+ 1,5 x Qp + 1,5 x Qa =55,955 KN/mq

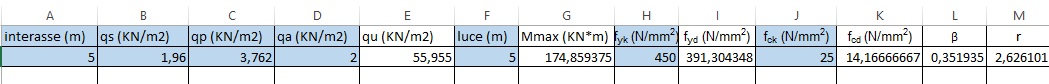
Anche per la tipologia in calcestruzzo armato è stato calcolato Mmax, che, ancora una volta è stato trovato considerando la trave doppiamente appoggiata quindi:

Mmax= q x l ^2 /8

Una volta inserita la resistenza caratteristica dell'armatura (fyk= 450 N/mmq) e, la resistenza caratteristica a complessione del CLS (fck= 25 N/mmq), ho ricavato l'altezza della mia trave ipotizzando una base di partenza di 40 cm, quindi H > Hmin. Ho scelto una sezione con B=40 cm ed H= 55 cm.

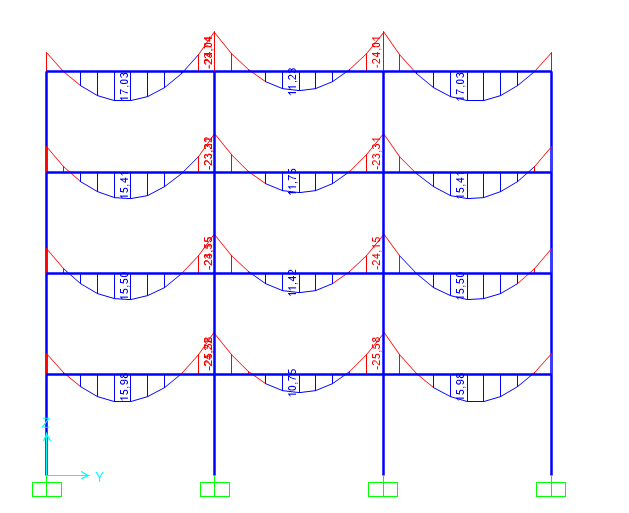
Il Mmax agente sulla trave ricavato dal modello SAP è di 25 KN* m e quindi è verificato per la mia sezione.

 

PILASTRO

Per dimensionare il pilastro più sollecitato in CLS sono sempre partita dallo sforzo normale ed ho calcolato i vari parametri, la scelta della sezione ha tenuto conto del fatto che ð < fcd, tenendo conto di  questa condizione posso verificare la sezione scelta che in questo caso è:

b= 30 cm      h= 50 cm.

 

 

 

SOLAIO IN LEGNO

 

 

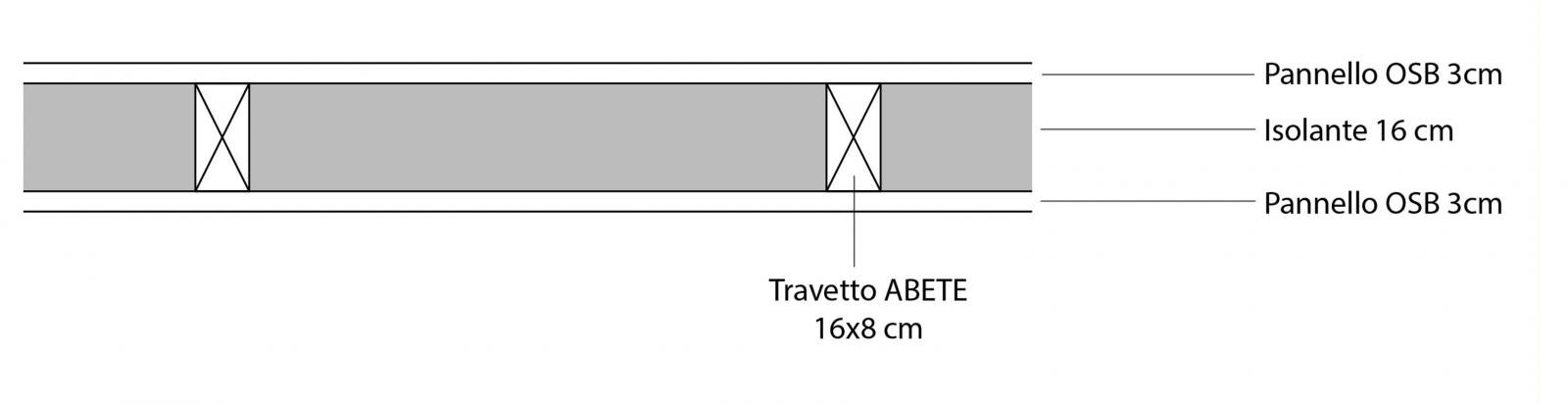
Sovraccarico Strutturale (Qs)

- Travetto in abete: S= 16x8 cm    ý= 450 Kg/mc

     pp:0,128x4,5= 0,576 x 2= 1,152 KN/mq

Qs= 1,152 KN/mq

 

Sovraccarico Permanente (Qp)

- OSB: S=0,03 m    ý= 650 Kg/mc

   pp: 0,03x6,5=0,195 x 2= 0,39 KN/mq

- Isolante: S=16 cm    ý= 15 Kg/mc

    pp: 0,15x0,16= 0,024 KN/mq

Incidenza impianti= 0,5 KN/mq

Incidenza impianti= 1 KN/mq

Qp= 1,914 KN/mq

Sovraccarico accidentale (Qa)

Qa= 2 KN/mq

Qu= 1,3 x Qs+ 1,5 x Qp + 1,5 x Qa =36,843 KN/mq

Scelta la tipologia del legno posso ricavare alcuni valori caratteristici del materiale.

Imposto una base della trave b = 35 cm e tramite Hmin = √6 x Mmax / fmd x b ricavo il valore dell’altezza minima che dovrà avere la trave.
Quindi H > Hmin      Hmin = 24,48 cm
H = 50 cm

Dalla figura precedente si puù vedere il valore di Mmax agente sulle trave ricavato da SAP.

 

PILASTRO

Per quanto riguarda il dimensionamento del pilastro più sollecitato abbiamo  calcolato lo sforzo Normale su ogni piano,

N.1 piano = (A inf x Qu) + Peso Travi
formula in cui il Peso delle Travi è pari a = (A trave x La + A trave x Lb) x γ

Successivamente abbiamo moltiplicato lo sforzo Normale per ogni piano x il numero di piano ed ottenuto Nmax= 1784,81 KN

In un ulteriore foglio excel si è inserito come dato di partenza proprio lo sforzo Normale max per andare a ricavare le dimensioni della base e dell’altezza del pilastro in legno. In questo caso b = 35 cm e h = 50 cm 

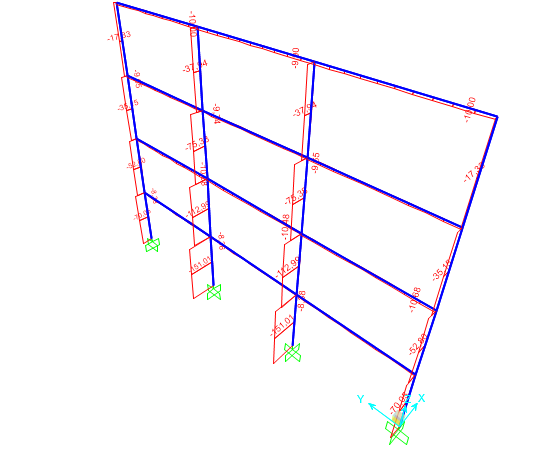
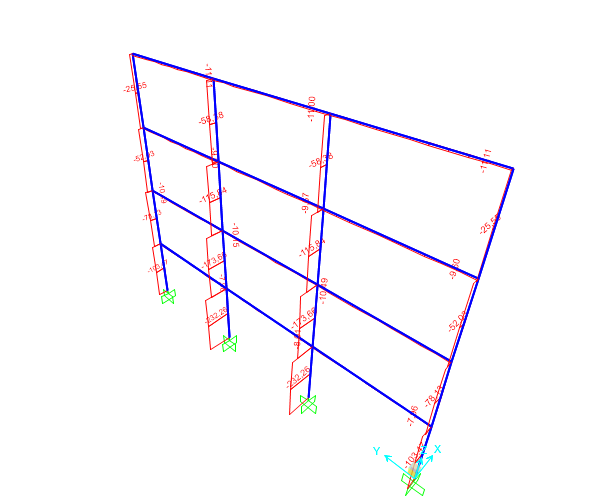
Per ogni tipologia costruttiva è stato analizzato lo sforzo assiale agente sui pilastri attraverso SAP, per verificarne la correttezza delle diverse sezioni scelte.

 

Elaborato svolto in coppia: Mariucci Serena-Taiariol Beatrice