-trave principale: luce 6m, interasse 3m, legno gl28h
Come nel caso precedente procedo al dimensionamento della trave principale mantenendo il valore dei carichi calcolati per il travetto integrando Qs con il carico relativo alla travatura secondaria.
Qs:
Tavolato 6 KN/mc*0,03m= 0,18 KN/mq
Travetto 10X16 3,8*0,1*0,16*1*1/0,5= 0,08 KN/mq
Di nuovo con il foglio elettronico, scegliendo questa volta una base di 28cm, ottengo un’altezza minima di 37,21cm. Cercando quindi sempre di mantenere un rapporto ideale tra base e altezza scelgo una sezione 28X40.
Aggiungendo infine il peso della trave al peso a mq (q) e ricalcolando l’altezza con la medesima base constato anche in questo caso di ottenere sempre un’altezza inferiore a quella scelta e quindi la sezione è verificata.

3 | STRUTTURA IN CLS ARMATO
Dimensionamento
-trave principale: luce 6m, interasse 3m, acciaio B450c (per zone sismiche), cls C40/50
Qa:
Locali d’abitazione 2,00 KN/Mq
Qp:
Pavimento linoleum 0,10 KN/mq
Massetto 18 KN/mc*0,04m= 0,72 KN/mq
Isolante 7 KN/mc*0,01m= 0,07 KN/mq
Intonaco 10 KN/mc*0,015m= 0,15 KN/mq
Incidenza tramezzi e impianti 1,50 KN/mq
Totale 2,54 KN/mq
Qs:
Pacchetto 16+4
travetti/pignatte+soletta 2,36 KN/mq
Inserisco i valori nel foglio elettronico e, scegliendo una base di 20cm, ottengo un’altezza totale minima di 29,73cm. Vista la stretta prossimità al valore 30 scelgo un valore superiore altrimenti la sezione non verrebbe verificata. Perciò la mia scelta ricade sul 20X35 e, aggiungendone il peso ai carichi (q), otteniamo un’altezza minore di quella adottata. Tutto è quindi verificato.
2 | ESERCITAZIONE DIMENSIONAMENTO RETICOLARE SPAZIALE
Lo scopo della presente esercitazione è dimensionare le aste di una reticolare spaziale. Il procedimento inizia in ambiente CAD dove viene disegnata la reticolare partendo da un modulo bidimensionale di aste lineari e diagonali per poi arrivare dapprima ad un modulo tridimensionale ed infine ad una maglia di dimensioni 4X6.
Una volta completata la struttura la importiamo in Sap tramite file DXF al fine di ricavarne gli sforzi di trazione e compressione nelle aste.
1 - Inizialmente occorre definire i vincoli interni concretizzando quindi i nodi della reticolare;
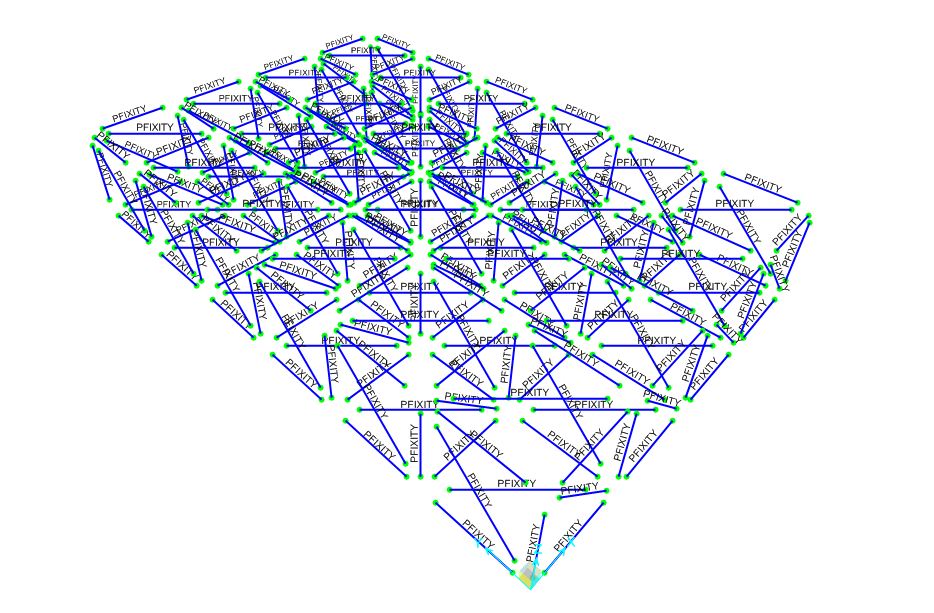
2 - Definisco poi i vincoli esterni posizionando le cerniere nelle quattro estremità inferiori;

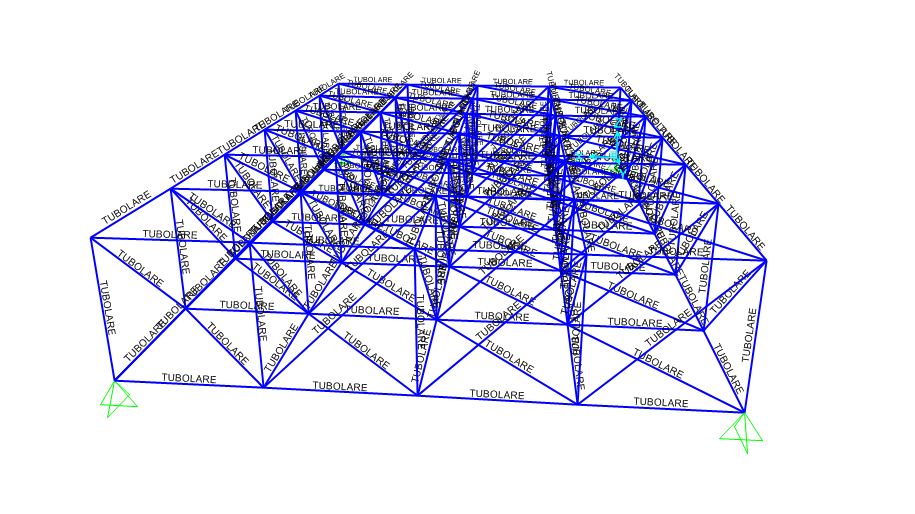
3 - A questo punto definisco materiale e sezione dei profili delle aste, che nel mio caso assumeranno una forma tubolare in acciaio;
4 - Non resta quindi che sottoporre la struttura a dei carichi e nel mio caso a forze concentrate su tutti i nodi superiori di intensità 40 KN.
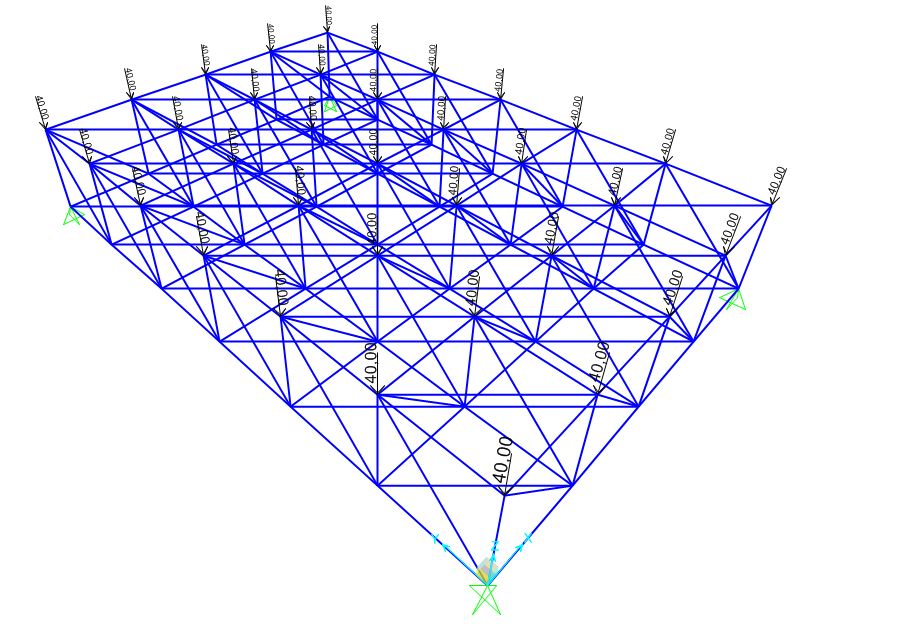
Analizzando la struttura e le sue deformazioni posso ora osservare la distribuzione delle tensioni che, opportunamente tabellate, mi consentono di individuare le aste maggiormente sollecitate a trazione e a compressione.
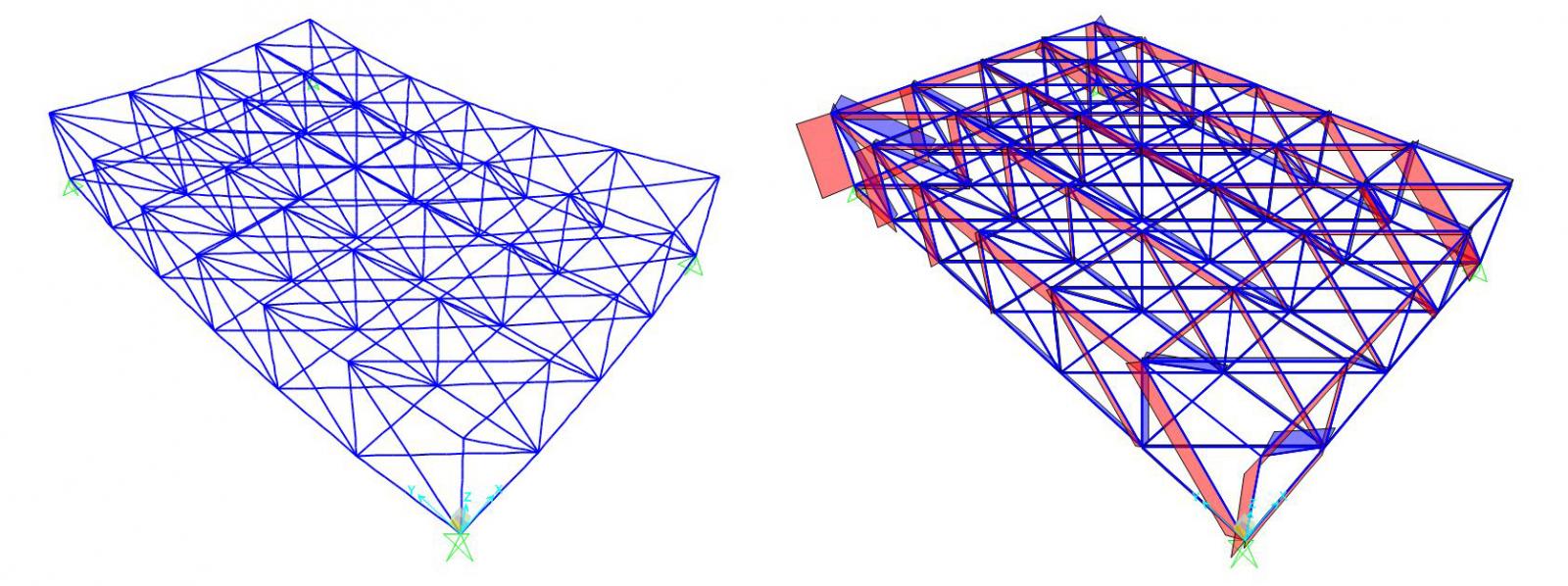
VALORI TENSIONI MASSIME
ASTA LINEARE
296,4 KN | compressione
ASTA DIAGONALE
307,3 KN | compressione
256,6 KN | trazione
COMPRESSIONE
1- Asta lineare ( l=2m ) | acciaio FE510 S355
PROGETTO:
Inizialmente si ottiene la tensione ammissibile ricavandola dal rapporto fra la tensione di snervamento e il coefficiente di sicurezza di 1,05:
fd = 35,5 / 1,05= 33,80 KN/cmq
L’area minima che ne risulta è pari a
Amin= N/fd= 296,4/33,80= 8,77 cmq
Scelgo quindi in questo caso una sezione TUBOLARE di 9,65cmq
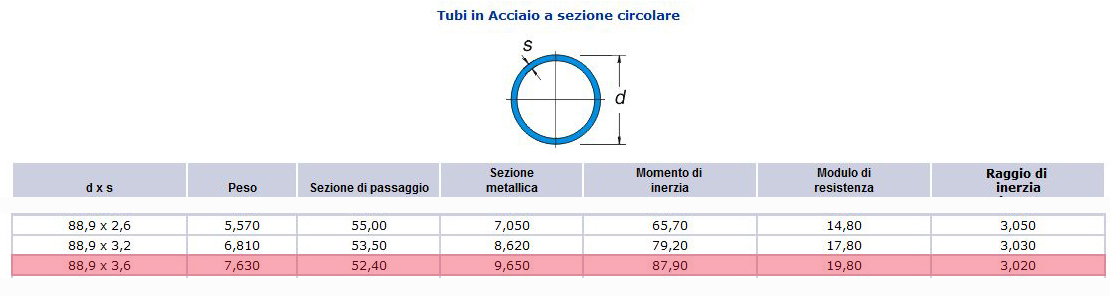
VERIFICA:
La tensione massima pari al rapporto fra il carico massimo e l’area della sezione scelta vale
σ=N/A= 296,4/9,65= 30,72KN/cmq < 33,8 e quindi VERIFICATO
CARICO CRITICO EULERIANO:
Nel caso di sforzo a compressione occorre tener presente il fenomeno del carico di punta e quindi calcolare la situazione di carico massimo che non bisogna raggiungere ovvero Pcrit= (π2*E*J)/lo2 dove E è il modulo elastico a compressione, J il momento d’inerzia minore e lo la lunghezza libera di inflessione.
Pcrit= (3,142*210000N/mmq*879000mmq)/20002mm= 454995N= 455KN
Pcrit risulta molto più grande del carico a compressione e quindi le aste non risultano soggette a carico di punta.
2- Asta diagonale ( l=2,83m ) | acciaio FE510 S355
PROGETTO:
Si utilizza lo stesso tipo di acciaio del caso precedente e quindi fd ha sempre valore 33,80 KN/cmq
In questo caso, troviamo un risultato che poco si discosta dal caso dell'asta lineare
Amin= N/fd= 307,3/33,80= 9,09cmq
E di conseguenza anche in questo caso scelgo una sezione TUBOLARE di 9,65cmq
VERIFICA:
σ=N/A= 307,3/9,65= 31,84KN/cmq < 33,8 e quindi VERIFICATO
CARICO CRITICO EULERIANO:
Anche in questo caso per ovviare al problema del carico di punta calcolo il Pcrit che in questo caso risulta maggiore del carico cui è sottoposta l’asta.
Pcrit= (3,142*210000N/mmq*879000mmq)/28302mm= 227245N= 227KN<307KN NON VERIFICATO
Pertanto occore scegliere una nuova sezione di dimensioni maggiori e controllare nuovamente il carico critico.
Scelgo una sezione TUBOLARE di 12,5cmq
VERIFICA NUOVA SEZIONE:
σ=N/A= 307,3/12,5= 24,58KN/cmq < 33,8 e quindi VERIFICATO
CARICO CRITICO EULERIANO NUOVA SEZIONE:
Ora il carico critico è più basso del carico effettivo agente e quindi possiamo affermare con sicurezza che non si verificheranno problemi di carico di punta.
Pcrit= (3,142*210000N/mmq*1920000mmq)/28302mm= 496371N= 496KN>307KN VERIFICATO
TRAZIONE
Asta diagonale ( l=2,83m ) | acciaio FE510 S355
PROGETTO:
Analogamente alla compressione si ottiene la tensione ammissibile ricavandola dal rapporto fra la tensione di snervamento e il coefficiente di sicurezza di 1,05:
fd = 35,5 / 1,05= 33,80 KN/cmq
L’area minima che ne risulta ora è pari a
Amin= N/fd= 256,6/33,80= 7,59 cmq
Scelgo quindi in questo caso una sezione TUBOLARE di 8,62cmq
VERIFICA:
La tensione massima pari al rapporto fra il carico massimo e l’area della sezione minima scelta vale
σ=N/A= 256,6/8,62= 29,77KN/cmq < 33,8 e quindi VERIFICATO
Verificando l’asta diagonale che è sottoposta al maggior valore di trazione non risulta necessario verificare la trazione massima dell’asta lunga lineare.
3 | ESERCITAZIONE RIPARTIZIONE FORZE SISMICHE
L’esercitazione prevede la comprensione di come le forze sismiche si ripartiscono su un impalcato costituito da un certo numero di controventi. Abbiamo dunque una struttura simmetrica in cemento armato composta da 5 telai posti verticalmente e da 3 telai orizzontalmente.

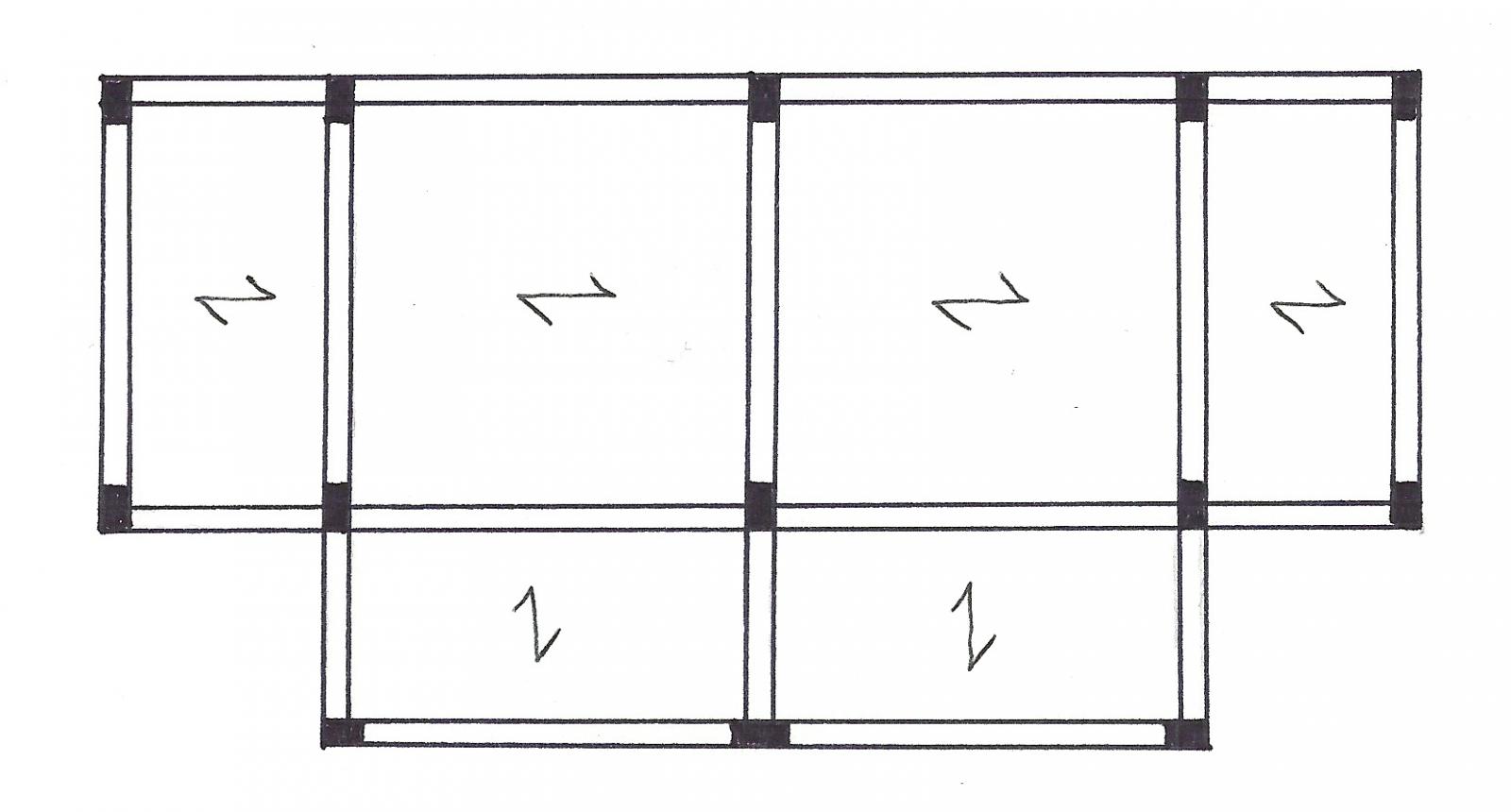
Lo schema dell’impalcato risulta quindi composto da 13 pilastri (30x40cm), disposti ed orientati parallelamente alla direzione delle travi principali su cui viene tessuto il solaio in modo tale che il momento d’inerzia maggiore della sezione del pilastro agisca sulla trave più lunga e maggiormente inflessa.
A questo punto mi rendo conto che la struttura con cui ho a che fare è iperstatica e per poterla risolvere sfrutto il fatto che i vincoli si comportano in maniera elastica e possono pertanto essere assimilati a delle molle la cui rigidezza è legata alla legge di Hooke (F = Kδ δ= F/K) ed è pari alla somma delle rigidezze dei singoli pilastri che si comportano come telai Sheat Type.
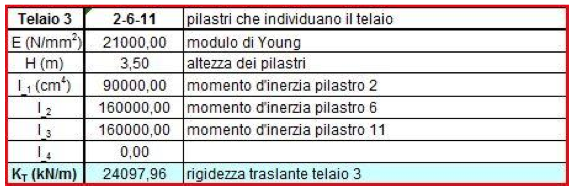
La rigidezza traslante in un telaio Shear Type è per ogni pilastro pari a K = 12EI/h3 con I pari al momento d'inerzia del relativo pilastro. Pertanto stabilito che l’altezza dei pilastri sarà pari a 3,50 m, la sezione 30 x 40 cm ed il materiale il cemento armato (il modulo di young sarà 21000 N/mm2), il calcolo della rigidezza traslante del controvento formato, ad esempio, dai pilastri 1-5-10 risulterà:
12x21000(90000+160000+160000)/3,5^3=24097,96 KN/m


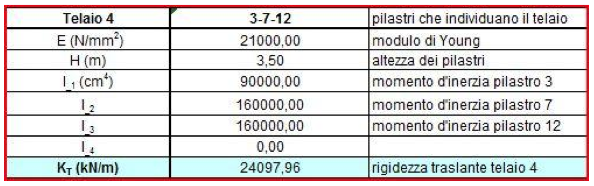
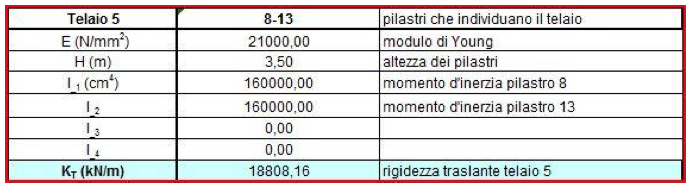

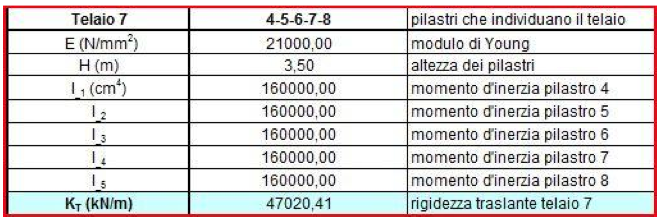
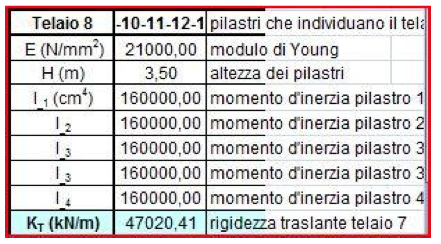
Assegnamo ora un origine di riferimento 0. Questa ci tornerà utile per definire inanzitutto le distanze da questa delle rigidezze traslanti verticali e orizzontali dv e do e le coordinate delle aree in cui abbiamo scomposto la figura principale.


Sfruttando a questo punto le diverse aree e le relative coordinate sono in grado di ricavare il centro di massa della struttura (punto in cui agisce la forza sismica):
XG=(A1*XG1+A2*XG2)/(A1+A2)= 18
m
YG=(A1*YG1+A2*YG2)/(A1+A2)= 9,75 m
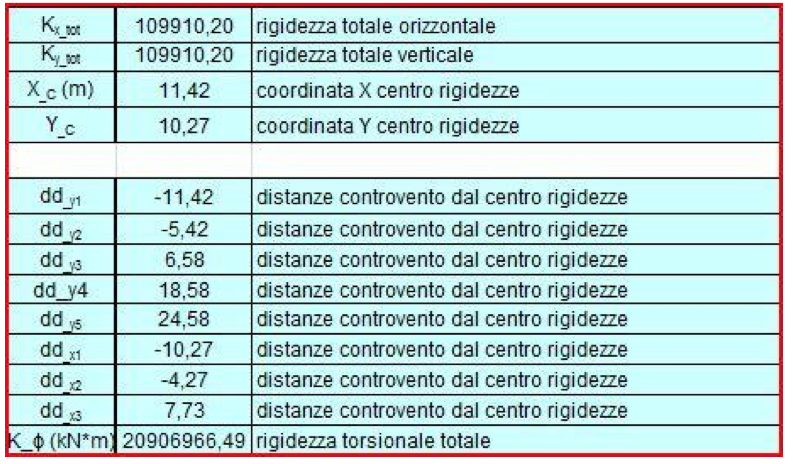
I controventi vengono inseriti per vincolare la struttura alle forze orizzontali. Essi sviluppano delle forze alle quali i pilastri reagiscono con la loro rigidezza. Per capire come la struttura ruoterebbe è necessario individuare il centro delle rigidezze, centro di rotazione che rimane fermo mentre il resto della struttura ruota.
Le formule per calcolarne le coordinate sono le seguenti:
Xc= (K2y*d2y+K3y*d3y+ K4y*d4y)/Ky tot
Yc=( K2x*d2x+K3x*d3x+ K4x*d4x)/Kx tot
Una volta trovate le coordinate del centro delle rigidezze si potrà trovare la distanza di ciascun controvento da tale centro sottraendo la distanza orizzontale dal punto di riferimento di ciascun controvento verticale alla coordinata x del centro delle rigidezze, e la distanza verticale dal punto di riferimento di ciascun controvento orizzontale alla coordinata y del centro delle rigidezze.
Si potrà ora conoscere la rigidezza torsionale totale moltiplicando la rigidezza traslante di ciascun controvento per la propria distanza al quadrato dal centro delle rigidezze utilizzando quindi la formula ∑i Ki ddi^2
A questo punto possiamo calcolare il peso sismico grazie alla formula W=G+yQ dove G=(qs+qp)*Atot
è il sovraccarico permanente comprensivo della struttura e dei carichi fissi mentre Q=qa*Atot è comprensivo dei carichi accidentali e viene moltiplicato per il coefficiente di contemporaneità pari a 0,8 e dovuto al fatto che i carichi accidentali possono anche non essere presenti durante il sisma.
Trovato il peso sismico possiamo calcolarci la forza sismica orizzontale , forza d’inerzia dovuta al movimento del suolo, che può essere definita come massa del corpo per accelerazione di trascinamento.
Sappiamo che F=ma e che a=c*g dove c è il coefficiente di intensità sismica. Possiamo quindi scrivere F=(mg) c dove mg è il peso della struttura, quindi la forza sismica è una porzione di tale peso.
Visto che il nostro peso corrisponde al W possiamo riscrivere l’equazione come F=W*c
La rotazione della struttura può avvenire se la forza non passa per il centro delle rigidezze. Quando la struttura ruota viene a crearsi un momento torcente.
M=F(Yc-Yg) dove F è la forza sismica precedentemente calcolata e yg-yc è il braccio dato dalla differenza tra la coordinata del centro delle rigidezze e quella del centro di massa.
Infine attraverso le ultime due tabelle, una relativa alla ripartizione delle forze sismiche lungo x e l’altra lungo y, possiamo ricavarci il MOMENTO TORCENTE la TRASLAZIONE DELL’IMPALCATO nelle due direzioni (F/Ktot), e la ROTAZIONE DELL’IMPALCATO ψ=M/Kψtot, e permettono di vedere come la forza sismica si ripartisce su ciascun controvento attraverso la formula:
Rx=Kx(Ux+ψddx) per i controventi orizzontali
Ry=Ky(Uy+ψddy) per i controventi verticali
_______________________________________________________________________________________________________________________ SCILLA FRANCESCO | bilancia | 453412
Commenti recenti