blog di alice.zaratti

Dato l'impalcato in figura, progettato in cemento armato, si procede all'individualizzazione del centro delle rigidezze.

Per trovare il centro delle rigidezze, bisogna trovare il centro di massa.

La struttura non ha una forma geometrica di base, quindi per conoscere il suo baricentro si deve suddividere in superfici più piccole con geometrie di cui si conosce la posizione del centro di massa.

Si disegna l'impalcato su SAP con il suo centro di massa e si assegnano le sezioni.

Trave: 30x50m

Pilastro: 35x35m

Si impone a tutti i nodi dell'impalcato e al centro di massa la condizione di nodo rigido, in modo che tutti i punti ruotano dello stesso valore.

Si procede ad una prima analisi per trovare il peso della struttura.

Per trovare la forza sismica, si dovrà moltiplicare il peso dell'impalcato per un coefficente di intensità sismica, dato dalla normativa.

In questo caso, si considera l'edificio costruito in una zona a basso rischio sismico, prendendo come coefficente 0,2.

Applico la forza sismica al centro di massa, nelle due direzioni principali x ed y.

Facendo l'analisi si nota come, lungo x e lungo y l'impalcato subisce delle rotazioni.

Lungo x Lungo y 

Ci si rende conto che il centro di massa ed il centro delle rigidezze non coincidono, quindi si sposta il centro di massa fino ad annullare la rotazione in entrambe le direzioni.

Il centro delle rigidezze dell'impalcato è distante dal centro di massa, in particolare ha coordinate:

In questo caso si procede all'avvicinamento del centro delle rigidezze al centro di massa, agendo o sulla geometria della struttura, per esempio rendendola più simmetrica spostando un setto o aumentando la rigidezza degli elementi nella parte meno rigida della struttura.

Si procede al dimensionamento di un graticcio 12x18m, con modulo 1x1m.

Si considera, per questa esercitazione, che non si conosce il posizionamento dei pilastri, ma si conosce il numero di piani che il graticcio deve sorreggere.

Per questo motivo si andranno ad applicare dei carichi distribuiti sulle travi.

Si sceglie il tipo di solaio da utilizzare e con il foglio excel si calcolano i carichi qp, qa e qs.

Il carico iniziale da applicare sulle travi è dato dai soli qp e qa in modo da progettare una sezione che sia in grado di sorreggere i carichi alla quale sarà sottoposta.

qp*1,5+qa*1,5= 11,778kN/m²

Per applicare il carico si tiene conto dell'area d'influenza di ogni trave, che ai bordi sarà dimezzata.

qu*Anf*n°piani=q1

Facendo l'analisi con SAP si avrà una deformata e delle sollecitazioni pari a quelle di una trave doppiamente incastrata, avendo vincolato solo i lati al bordo, quindi le sezioni più sollecitate saranno quelle all'estremità.

 Dalle tabelle di SAP si individua il valore massimo, che servirà per dimensionare la struttura.

Si procede al dimensionamento, prendendo in considerazione sia il calcestruzzo sia i tondini d'armatura.

Il foglio troverà l'altezza utile, ed infine l'altezza minima della sezione.

La trave trovata ha una sezione di 30x80m.

Come conferma del giusto dimensionamento, si assegna su SAP la sezione appena ingegnerizzata e si verifica che sia in grado di sorreggere il proprio peso, oltre a quello dei carichi, applicando come carico qs, con il peso proprio. 

Si trova il momento massimo e si procede al nuovo dimensionamento.

La trave progettata in precedenza è in grado di sorreggere la struttura, ci si rende conto che è anche sovraddimensionata, quindi si può ridurre la sezione a 30x75m.

Per ultimo si procede alla verifica dell'SLE (stato limite d'esercizio).

L'abbassamento massimo non deve superare 1/200 della luce.

Vmax: -0,02253m

l/200: 0,055m

Vmax<l/200, la struttura è verificata.

L'esercitazione prevede il dimensionamento della Trave e del Pilastro più sollecitati di un telaio, considerando tre soluzioni tecnologiche differenti: Legno, Acciaio e Cls armato.

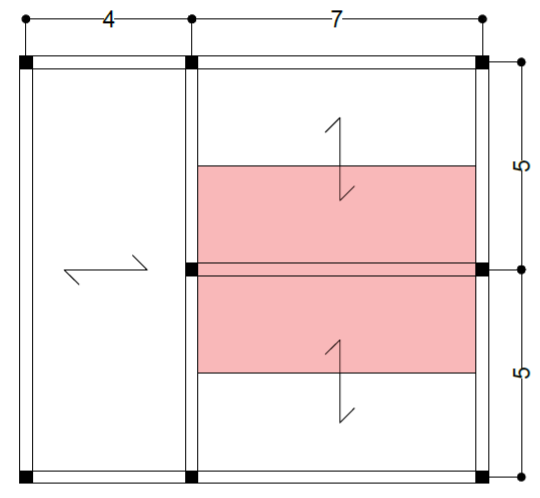
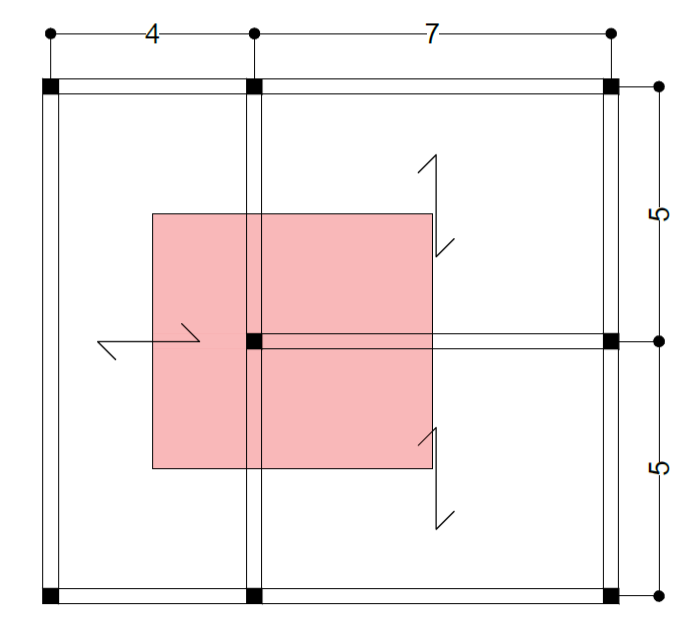
LEGNO

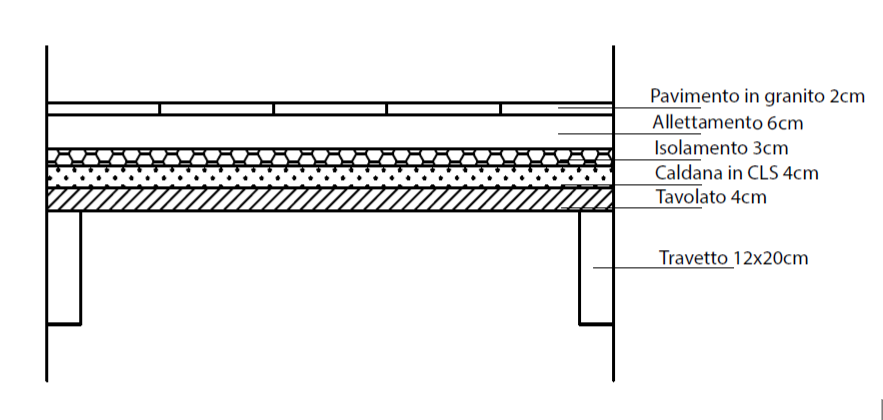
Dopo aver scelto la tipologia di solaio, iniziamo calcolando i carichi che agiscono su di esso.

Questi si dividono in:

qs, carichi strutturali, dati da tutti gli elementi che hanno funzione strutturale

qp, carichi permanenti, dati da tutti gli elementi presenti nel solaio ma che non hanno funzione strutturale

qa, carichi accidentali, dati dalla normativa, in questo caso qa=2kN/m² perchè si considera la destinazione d'uso abitativa

il valore dei carichi si ottiene moltiplicando il volume di tutti gli elementi, a m², per il loro peso specifico, in particolare:

qs:

Travetto in legno: 0,16 kN/m²

Tavolato in legno: 0,20 kN/m²

Gettata in CLS: 1,00 kN/m²

TOT: 1,36 kN/m²

qp:

Pavimento: 0,02mx0,6kN/m³=0,012 kN/m² 

Allettamento: 0,06mx19kN/m³=1,14 kN/m²

In questo caso si tiene conto anche dell'incidenza dei tramezzi e degli impianti, per un valore pari a 2,5 kN/m²

TOT: 2,68 kN/Mm²

TRAVE

Fissata la luce il foglio calcola il momento massimo della trave, pari a q_ul²/8

 

Ora scelgo la classe di resistenza del materiale, in questo caso C24, dove F_mk=24 N/mm² .

conoscendo F_mk, il foglio calcola la tensione di progetto che è pari a F_md .

K_mod è un fattore che tiene conto del degrado del materiale.

Trovata la resistenza di progetto posso fissare una base, presa da un profilario e trovo il profilo con resistenza subito maggiore a quella trovata.

Fissata la base, i dati mi permettono di trovare l'altezza minima, infine la ingegnerizzo.

PILASTRO

Parto calcolando l'area d'influenza del pilastro e inserendo l'area della trave precedentemente trovata.

Assegnato il peso specifico del materiale, in particolare 6 kN/m³ (Abete rosso) posso calcolare il peso delle travi agenti sul pilastro.

Avendo il carico ed il peso delle travi agenti sul pilastro, il foglio calcola inizialmente lo sforzo normale per un piano.

Poi aggiungendo il numero dei piani trovo lo sforzo normale massimo, N_max 

Dato N_max e F_md posso trovare l'area minima che il pilastro deve avere per sopportare i carichi agenti.

Fissati E ( dato dalla classe di resistenza) , la luce e ß (coefficente che dipende dalla condizione di vincolo) posso trovare: la snellezza, il raggio d'inerzia minimo che mi permetteranno poi di trovare la base e l'altezza minima della sezione del pilastro. 

Ora posso ingegnerizzare, ovvero dare alla base e all'altezza dei valori reali che si possono trovare sul mercato.

Ora calcolo A_design , ovvero l'area della sezione progettata che, per essere verificata deve essere maggiore dell'area minima trovata in precedenza.

In questo caso A_min < A_design , quindi la sezione è verificata.

 

ACCIAIO

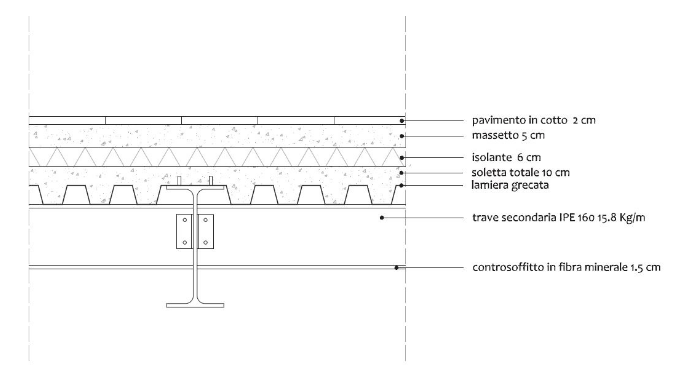
Si procede con il calcolo dei carichi 

qs: 1,8 kN/m²

qp: 2,15 kN/m²

TRAVE

Trovo il momento massimo della trave come q_ul²/8.

Scelta la classe di resistenza del materiale, S275, avrò f_yk=275 N/mm²

Il foglio calcola la tensione massima di progetto f_yd

Nel caso dell'acciaio è necessaria una verifica a flessione della trave e solo trovando il modulo di resitenza a flessione minima, W_min, potrò scegliere il profilo in grado di sopportare i carichi agenti

Trovata W_min, la ingegnerizzo, andando sul tabulario e prendendo il profilo con resistenza a flessine subito maggiore a quella trovata. 

In questo caso si tratta di un IPE400

PILASTRO

Come visto in precedenza, il foglio calcola l'area d'influenza del pilastro, inserendo le luci, e il peso delle travi, inserendo il peso specifico del materiale e l'area della trave.

Successivamente il foglio calcolerà il carico ultimo q_u 

Con i dati inseriti il foglio calcolerà prima lo sforzo normale per un piano, poi per tutti i piani della struttura (Nmax)

Dato Nmax e f_yk il foglio calcolerà f_yd e A_min

Fissati E, la luce e ß posso trovare: la snellezza, il raggio d'inerzia minimo che mi permetteranno poi di trovare il momento l'inerzia minimo della sezione del pilastro.

Con i dati ottenuti dal profilario delle travi HE trovo il profilo con I_min appena superiore a quello trovato, facendo attenzione che l'area della sezione sia comunque superiore a quella trovata in precedenza.

In base a queste considerazioni il profilo trovato per il pilastro è HEA120

CALCESTRUZZO

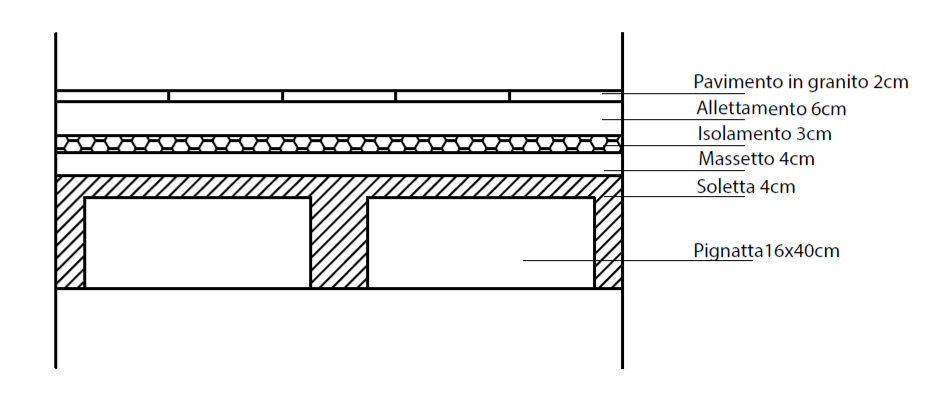
Trovo i carichi

qs:2,5 kM/m²

qp:3,85 kN/m²

TRAVE

Il foglio calcolerà il carico ultimo q_u e, successivamente, inserendo la luce, M_max

 Nel caso del calcestruzzo il dimensionamento è diverso perchè nella trave abbiamo due materiali, il calcestruzzo e l'acciaio (i tondini d'armatura), quindi nella progettazione della trave bisogna tener conto di due resistenze:

f_yk la resistenza caratteristica a flessione dell'acciaio

f_ck la resistenza caratteristica a compressione del calcestruzzo

Il foglio calcolerà le due resistenze di progetto f_yd e f_cd

Successivamente calcolerà due fattori: r e alfa , che sono due coefficenti che ci permettono di calcolare l'altezza utile, cioè l'altezza reagente della sezione, che si basa sull'ipotesi della conservazione delle sezioni piane e sul fatto che il calcestruzzo reagisca solo a compressione.

Fissata la base il foglio calcolerà h_u.

Si troverà infine l'altezza minima della trave, aggiungendo ad h_u il contributo del copriferro e del raggio del tondino.

Infine la ingegnierizziamo.

PILASTRO

Il procedimento iniziale del pilastro è uguale agli altri materiali presi in considerazione in precedenza.

Calcolati A_inf,P_travi e q_u il foglio calcolerà, prima N1piano (relativo ad un piano solo) e, successivamente, Nmax.

Con N_max e f_cd il foglio calcola A_min

Fissati E, la luce e ß, il foglio calcolerà, prima la snellezza ed il raggio d'inerzia minima, con i quali, successivamente, il foglio calcolerà la base e l'altezza minime della sezione del pilastro.

Ora si ingegnerizza la sezione, trovando b_design, h_design ed infine A_design

Il pilastro deve essere sottoposto alla verifica di presso-flessione, per questo motivo, inserendo il momento massimo generato dalla struttura precedentemente analizzata, 

si procede al calcolo del modulo di resistenza a flessione massimo e, successivamente, della tensione massima ammissibile, che per essere verificata non deve essere maggiore della tensione di progetto del materiale.