blog di Angelo.Mizzon

Esercitazione svolta con Marta Massacesi e Alessandra Tagliatesta 

In questa esercitazione dobbiamo studiare un piano di un edificio e trovare la posizione del centro delle rigidezze, e vedere che sia il più possibile vicina al centro di massa, in modo che, in caso di sisma, vengano evitate le rotazioni dell’edificio.

L’edificio analizzato presenta una struttura di travi in acciaio che poggiano su due blocchi scala/ascensore in cemento armato, che svolgono una funzione portante. 

Disegno la struttura su SAP2000 e assegno le sezioni ai vari elementi strutturali: per le travi scelgo delle travi IPE400 in acciaio S355, mentre per i setti portanti ipotizzo il calcestruzzo C35/45 con uno spessore di 30 cm. Poi vincolo la struttura a terra attraverso degli incastri

Per calcolare il carico relativo al sisma devo prima calcolare il peso proprio della struttura, poi moltiplico il peso strutturale per 0,2 (coefficiente per zone a basso rischio sismico).

Successivamente calcolo il centro di massa dell’edificio scomponendolo in figure semplici e calcolando il baricentro di ogni figura, con cui poi posso calcolare il baricentro totale della figura.

Xg = 26,71 m

Yg = 8,33 m 

Una volta disegnato il centro di massa su SAP2000 imposto nei nodi trave-trave e trave-setto la condizione di impalcato rigido, in modo che la struttura del solaio si comporti come un corpo rigido.

Dopo di che assegno il carico alla struttura nel centro di massa lungo l’asse x e lungo l’asse y. Poi faccio partire l’analisi per vedere come reagisce la struttura ai carichi orizzontali. 

Come possiamo vedere dai risultati dell’analisi la struttura subisce solo traslazioni orizzontali e verticali, per cui possiamo dedurre che il centro di massa coinciderà con il centro delle rigidezze

Per iniziare scelgo di prendere in considerazione una trave reticolare di modulo 4 m x 4 m appoggiata su due corpi scala e la modello su sap. 

Inserisco come appoggi delle cerniere esterne e decido di utilizzare come materiale l’acciaio S355 e come sezione un tubolare cavo circolare da 0.15 m di diametro

Nelle travi reticolari i nodi interni si comportano come cerniere interne per cui applico alla trave il rilascio dei momenti 

 

Dopo di che eseguo l’analisi della trave applicando soltanto il peso proprio della struttura. Poi esporto le tabelle su excel in modo da poter calcolare il peso proprio della struttura sommando tutti i valori F3.

Calcolato il peso proprio della struttura devo stabilire il carico che grava su ogni nodo della struttura portato dai solai appesi.

Decido di analizzare un edificio alto 4 piani. Il peso del solaio è di 6,37 kN/m^2 e lo moltiplico per la superficie di un piano per trovare il carico di un singolo piano Q= 6,37 kN/m^2 x 288 m^2 = 1834,56 kN

Moltiplico Q per il numero dei piani e trovo il carico totale, a cui devo sommare il peso della struttura

F = Q x 4 =( 1834,56 kN x 4) + F3  = 7546,85 kN

Per trovare il carico da applicare ad ogni nodo divido F per il numero dei nodi   f= F/28 = 269,54 kN

Eseguo di nuovo l’analisi stavolta però facendo partire soltanto il carico puntuale sui nodi. Poi estraggo le tabelle e nella colonna P troverò i valori relativi allo sforzo normale, con cui poi andrò a dimensionare le aste tese e le aste compresse

    

Con questi valori vado a dimensionare le aste tese e le aste compresso su excel

ASTE COMPRESSE

ASTE TESE

 

Per questa esercitazione vogliamo dimensionare trave e pilastro maggiormente sollecitati di un telaio generico, che venga realizzato in c.a., acciaio e legno.

1.DEFINIZIONE DELL’IMPALCATO DEL SOLAIO

Il telaio strutturale presenta una maglia regolare di 5,00 m x 5,00 m. La trave centrale e il pilastro centrale sono gli elementi maggiormente sollecitati in quanto risultano essere quelli con la maggiore area di influenza del solaio. Per ogni tecnologia avremo delle stratigrafie e dei carichi agenti differenti, quindi considereremo i tre materiali separatamente.

2.CALCESTRUZZO ARMATO

2.a ANALISI DEI CARICHI

Qs (KN/m^2) = carichi strutturali

• Travetti (12x20 cm) = 25 kN/m^3 x 0,024 m^2 x 1/0,5 m = 1,2 kN/m^2
• Pignatte = 0,076 m^2 x 1/0,5 m x 6 kN/m^3 = 0,92 kN/m^2
• Soletta di completamento = 25 kN/m^3 x 0,04 = 1,00 kN/m^2
• TOT. = 3,12 kN/m^2

Qp (kN/m^2) = carichi permanenti

• Pavimento in grès ceramico (sp. 0,02 m x 20 kN/m^3) = 0,4 kN/m^2
• Isolante termico ( sp. 0,05 m) = 0,05 kN/m^2
• Incidenza dei tramezzi = 1 kN/m^2
• Incidenza degli impianti = 0,5 kN/m2
• TOT. = 1,95 kN/m^2

Qa (kN/m^2) = carico accidentale

• Civile abitazione = 2,00 kN/m^2
• TOT. = 2,00 kN/m^2

Qu =  (1,3qs x 1,5qp x 1,5qa) x 5,00 m =  49,91 kN/m

2.b DIMENSIONAMENTO A FLESSIONE DELLA TRAVE  

Uso lo schema semplice di trave doppiamente appoggiata quindi calcolo il momento come

Mmax = Qu x l^2 / 8 = 155,95 kNm

Poi scelgo quali classi di materiali usare sia per l’acciaio che per il calcestruzzo, che influenzeranno sia le proprietà che la geometria della sezione. Materiali scelti:

• ACCIAIO B450C  ( resistenza caratteristica acciaio fyk=450,00 Mpa)
• CLS C35/45 (resistenza caratteristica cls fck=35,00 Mpa)

Con questi valori posso calcolare le tensioni di progetto del calcestruzzo compresso e dell’acciaio.

Dai valori delle tensioni di progetto definisco hu per poi calcolare Hmin come Hmin= hu + δ

• δ (copriferro)
• hu (altezza utile della sezione)

Ponendo b=30 cm e δ=5 cm ottengo hmin=48,89 cm. Nel calcestruzzo armato si ingegnerizzano le sezione arrotondando per difetto per cui scelgo H=50 cm e verifico la sezione aggiungendo il peso delle travi.

2.c DIMENSIONAMENTO DEL PILASTRO IN CLS ARMATO

Comincio analizzando tutto il carico agente sul pilastro più sollecitato. All’analisi dei carichi effettuata in precedenza aggiungo il peso delle travi che incidono sul pilastro

Ptravi = (Atrave x l x γ) x 2 = (0,165 x 5 x 25 ) x 2 = 41,25 kN

Ora posso stimare il carico del solaio Qsolaio= qu x Ainf = 249,53 kN a cui aggiungo il peso delle travi. Poi moltiplico per il numero dei piani e ottengo il valore di Nmax.

Dal valore di Nmax posso calcolare l’area minima del pilastro facendo A=N/fcd. Successivamente procedo con il calcolo del raggio di inerzia minimo, che per il cls avendo sezione rettangolare ci permette di calcolare la base minima del pilastro. I parametri che inserisco sono:

E = modulo di elasticità

β=parametro legato ai vincoli del pilastro analizzato (in questo caso β=1)

l = lunghezza dell’elemento

Questi parametri ci permettono di calcolare il valore della snellezza e il raggio di inerzia minimo rispettivamente definite come:

λ=3,14 x (E/fyd)^0,5     e       ρmin = β x l / λ

Dopo aver calcolato il raggio di inerzia minimo posso calcolare la base minima della sezione facendo bmin=2x(3)^0,5xρmin. Ora possiamo calcolare anche l’altezza minima facendo la formula inversa hmin=A/bmin. Cosi facendo troviamo dei valori minimi che vanno ingegnerizzati. In questo caso scelgo di utilizzare una sezione 30 cm x 30 cm. 

2.d VERIFICA DELLA TRAVE E DEL PILASTRO IN CALCESTRUZZO ARMATO

Creo il modello del telaio su sap2000 ed oltre ai carichi qs, qp e qa aggiungo alla struttura la forza del vento Fv = 0,7 x i = 0,7 x 5 = 3,5 kN/m, e calcolo il valore delle sollecitazioni, per vedere se quest’ultima forza influisce sulla struttura.

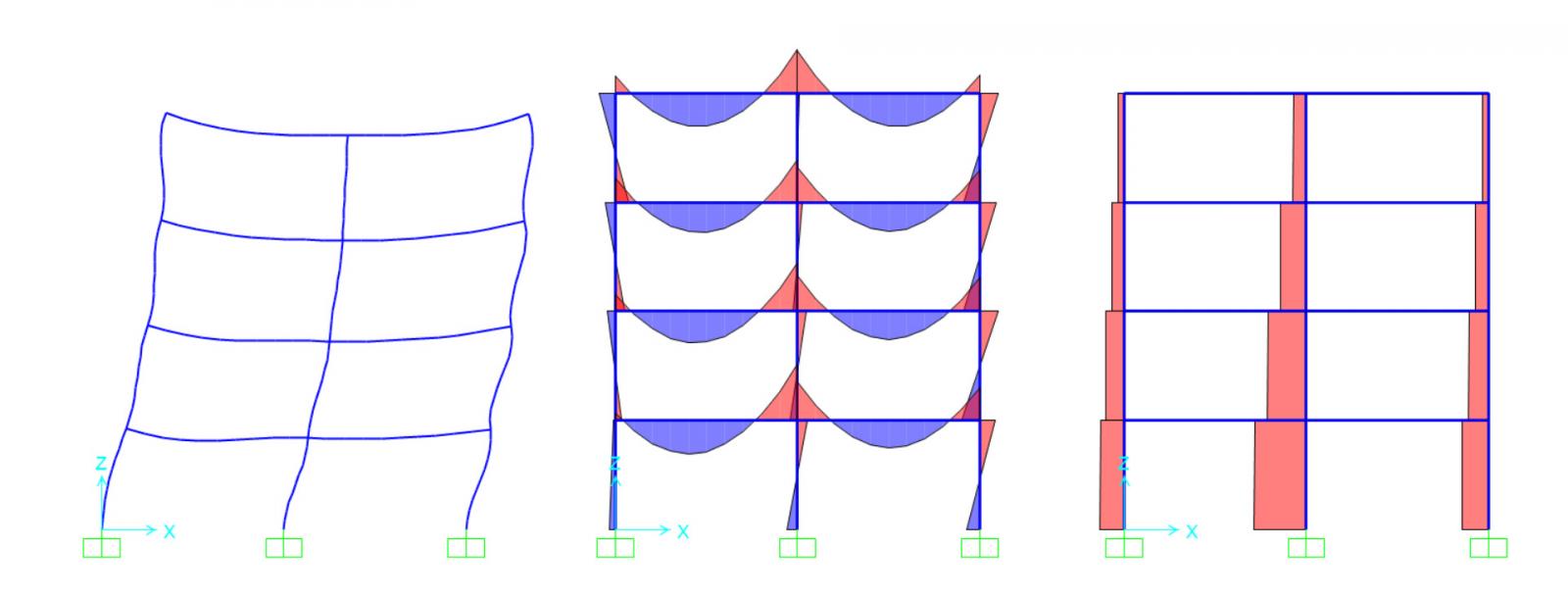
Controllo i valori sia del momento sia dello sforzo normale e verifico attraverso il foglio di calcolo se la sezione della trave e quella del pilastro che ho dimensionato sono sufficienti o dovranno essere incrementate.

verifica trave

verifica pilastro

Però per il calcestruzzo devo procedere anche con la verifica a pressoflessione in quanto siccome i nodi dei pilastri sono incastri c’è una trasmissione dei momenti, che sottopone i pilastri a pressoflessione.

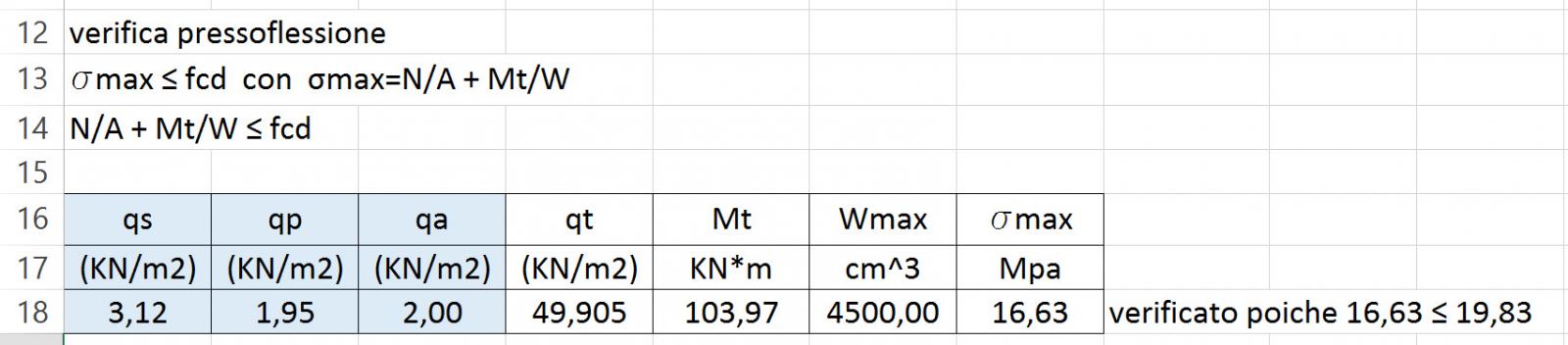
3. ACCIAIO

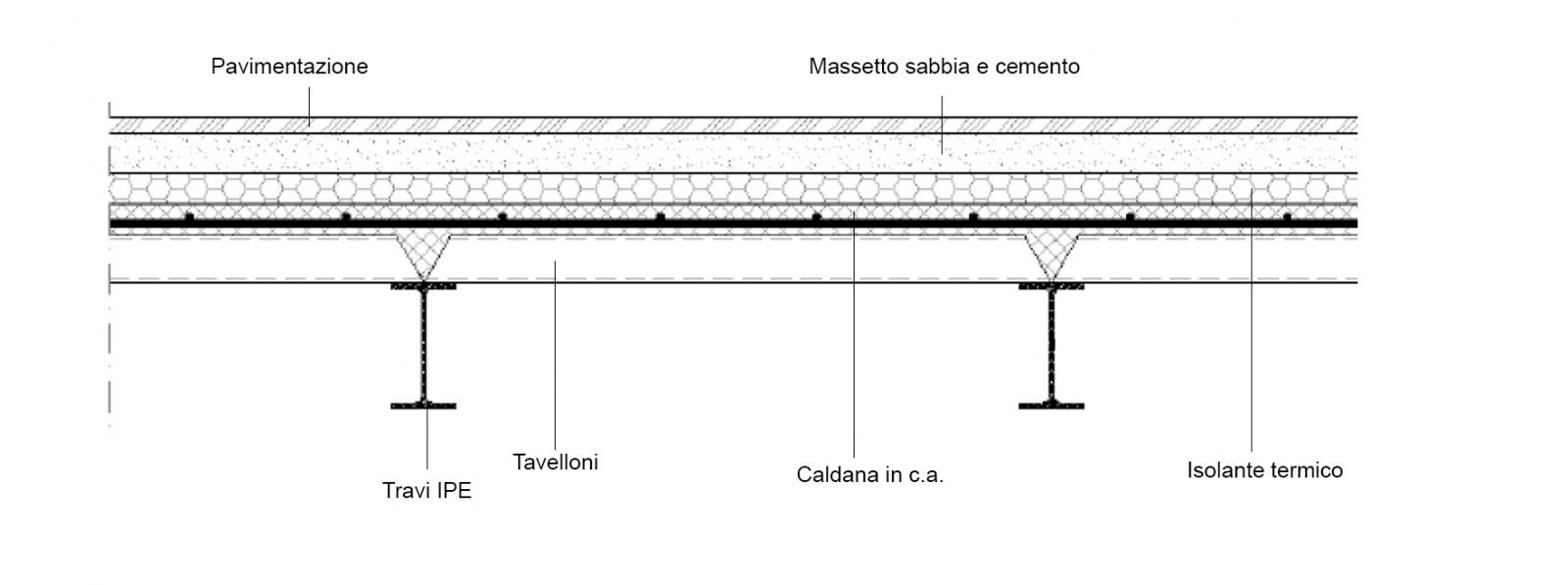
3.a ANALISI DEI CARICHI

Qs (KN/m^2) = carichi strutturali

• Travi IPE 160 = 78,5 kN/m^3 x 0,002009 m^2 x 1/0,8 m = 0,2 kN/m^2
• Caldana in c.a. = 25kN/m^3 x 0,04 m = 1,00 kN/m^2
• Tavelloni 250x800x60 (7,7 kg a pezzo) = 5 x 7,7 x 10/1000 = 0,39 kN/m^2
• Incidenza cls tra un tavellone e l’altro = 0,11 kN/m^2
• TOT.  1,70 kN/m^2

Qp (kN/m^2) = carichi permanenti

• Massetto sabbia e cemento = 18 kN/m^3 x 0,04 = 0,72
• Pavimento in grès ceramico (sp. 0,02 m x 20 kN/m^3) = 0,4 kN/m^2
• Isolante termico ( sp. 0,05 m) = 0,05 kN/m^2
• Incidenza dei tramezzi = 1 kN/m^2
• Incidenza degli impianti = 0,5 kN/m2
• TOT. 2,67 kN/m^2

Qa (kN/m^2) = carico accidentale

• Civile abitazione = 2,00 kN/m^2
• TOT. = 2,00 kN/m^2

Qu = (1,3qs x 1,5qp x 1,5qa) x 5,00 m =  46,08 kN/m

3.b MOMENTO MASSIMO

Mmax = Qu x l^2 / 8 = 143,98 kNm

3.c DIMENSIONAMENTO A FLESSIONE DELLA TRAVE

Per prima cosa scegliamo l’acciaio che vogliamo utilizzare per dimensionare la nostra trave. Ipotizziamo di usare un acciaio S275 avente tensione di snervamento fyk=275 Mpa e tensione di progetto fyd=261,9 Mpa. Per far si che la trave resista a flessione dobbiamo avere una situazione in cui il modulo di resistenza a flessione di progetto sia maggiore di quello minimo, quindi Wxmin < Wd.

Il modulo di resistenza a flessione minimo è dato da   Wxmin= Mmax/fyd

Nel caso in questione Wxmin = 549,76 cm^3, quindi dal sagomario scegliamo una trave che abbia un W maggiore di quello minimo, ovvero Wd= 557,10 (IPE300)

3.d DIMENSIONAMENTO DEL PILASTRO IN ACCIAIO

Comincio analizzando il carico agente sul pilastro più sollecitato. Per fare ciò calcolo il peso del solaio facendo Qsolaio= qu x Ainf = 230,38 kN, poi lo moltiplico per il numero dei piano e ottengo il valore di Nmax = 938,40 kN

Successivamente mettendo in relazione lo sforzo normale massimo Nmax e la tensione di progetto fyd posso ricavare l’area minima della sezione affinchè il materiale non entri in crisi.

Amin = Nmax/fyd = 35,83 cm^2

Fatta questa operazione, dobbiamo calcolare il raggio di inerzia minimo che ci permetterà di calcolare il momento di inerzia minimo della sezione. Arriviamo alla soluzione attraverso i seguenti parametri:

E = modulo di elasticità

β=parametro legato ai vincoli del pilastro analizzato (in questo caso β=1)

l = lunghezza dell’elemento

Questi parametri ci permettono di calcolare il valore della snellezza e il raggio di inerzia minimo rispettivamente definite come:

λ=3,14 x (E/fyd)^0,5     e       ρmin = β x l / λ

Dopo aver determinato il valore di ρmin posso calcolare il momento di inerzia minimo

Imin = A x ρ^2min

Quest’ultimo valore ci consentirà di scegliere dalle tabelle dei profilati, la sezione avente un valore del momento di inerzia minimo maggiore rispetto a quello ottenuto. Scegliendo il profilo avremo trovato l’Area di Design e il Momento di Inerzia di Design

3.e VERIFICA DELLA TRAVE E DEL PILASTRO IN ACCIAIO

Creo il modello del telaio su sap2000 ed oltre ai carichi qs, qp e qa aggiungo alla struttura la forza del vento Fv = 0,7 x i = 0,7 x 5 = 3,5 kN/m, e calcolo il valore delle sollecitazioni, per vedere se quest’ultima forza influisce sulla struttura.

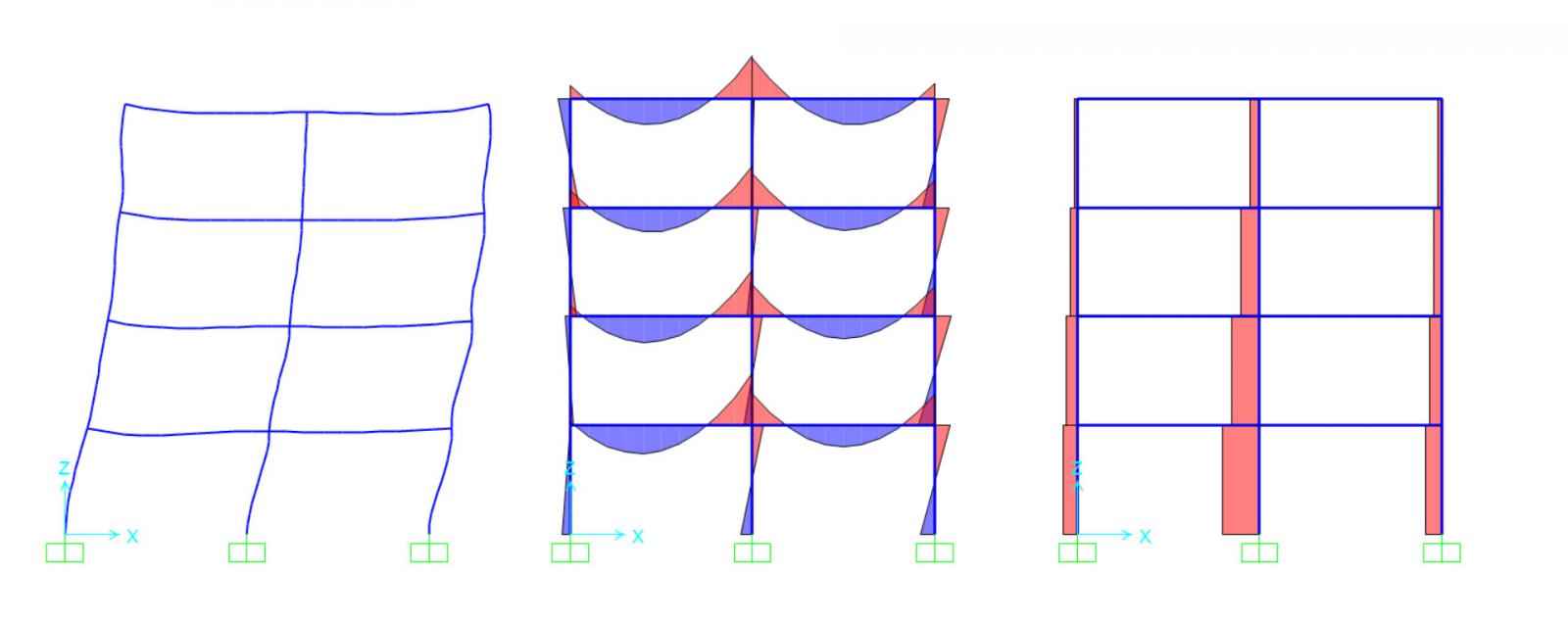
Controllo i valori sia del momento sia dello sforzo normale e verifico attraverso il foglio di calcolo se la sezione della trave e quella del pilastro che ho dimensionato sono sufficienti o dovranno essere incrementate.

verifica trave

verifica pilastro

La sezione della trave è verifica mentre quella del pilastro scelgo un profilato maggiore prendendo in considerazione non solo il momento di inerzia ma anche il parametro relativo all'area minima, quindi scelgo un HEA180.

4. LEGNO

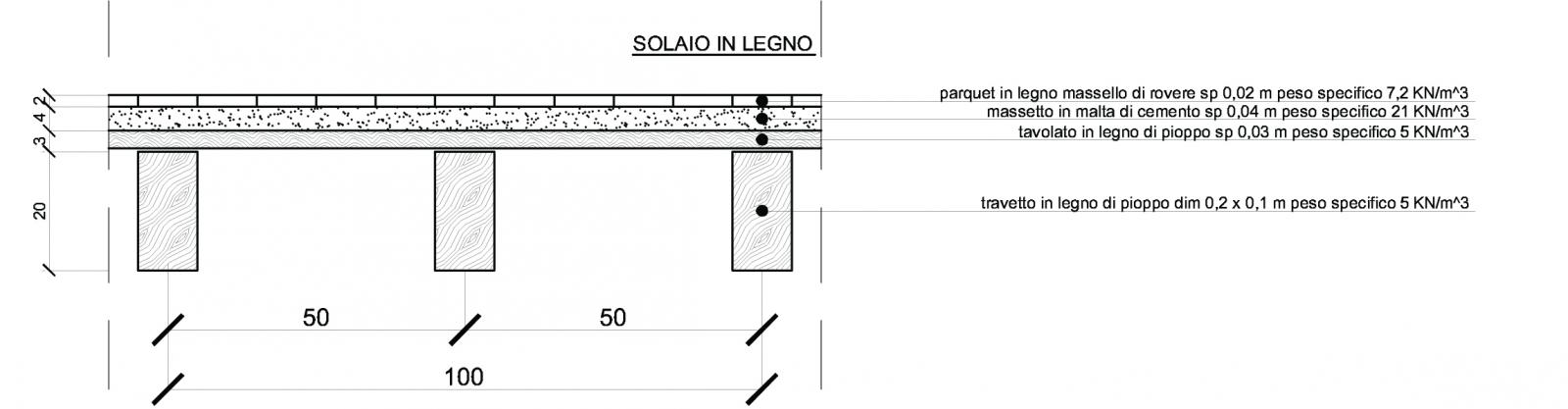
4.a ANALISI DEI CARICHI

Qs (KN/m^2) = carichi strutturali

• Travetti in legno di pioppo = 5 kN/m^3 x 0,02 m^2 x 1/0,5 m = 0,2 kN/m^2
• Tavolato in legno di pioppo = 5 kN/m^3 x0,03 m = 0,15 kN/m^2
• TOT. 0,35 kN/m^2

Qp (kN/m^2) = carichi permanenti

• Incidenza dei tramezzi = 1 kN/m^2
• Incidenza degli impianti = 0,5 kN/m2
• Isolante in fibra di legno = 0,5 kN/m^3 x 0,05 m = 0,025 kN/m^2
• Massetto in malta di cemento = 21 kN/m^3 x 0,04 m = 0,84 kN/m^2
• Parquet in legno massello di rovere = 7,2 kN/m^3 x 0,03 m = 0,22 kN/m^2
• TOT. 2,58 kN/m^2

Qa (kN/m^2) = carico accidentale

• Civile abitazione = 2,00 kN/m^2
• TOT. = 2,00 kN/m^2

Qu = (1,3qs x 1,5qp x 1,5qa) x 5,00 m =  36,63 kN/m

4.b DIMENSIONAMENTO A FLESSIONE DELLA TRAVE IN LEGNO

Uso lo schema semplice di trave doppiamente appoggiata quindi calcolo il momento come

Mmax = Qu x l^2 / 8 = 114,45 kNm

Uso un legno massiccio con resistenza caratteristica fmk=24 Mpa. Dopo di che calcolo la tensione di progetto che dipende da due fattori:

• Kmod, che tiene conto della durata del carico e delle condizioni climatiche (0,8)
• γm, ovvero il fattore di sicurezza del materiale (1,5)

Quindi calcolo fd=kmod x fmk / γm

Dopo di che scelgo b=30 cm e ricavo hmin come hmin= {[(6 x M_max) / (f_d x b)]}^0,5

Poi ingegnerizzo la sezione

4.c DIMENSIONAMENTO DEL PILASTRO IN LEGNO

Comincio analizzando il carico agente sul pilastro più sollecitato. Per fare ciò calcolo il peso del solaio facendo Qsolaio= qu x Ainf = 230,38 kN, poi lo moltiplico per il numero dei piano e ottengo il valore di Nmax =759,50 kN

Dal valore di Nmax posso calcolare l’area minima del pilastro facendo A=N/fcd. Successivamente procedo con il calcolo del raggio di inerzia minimo, che per il cls avendo sezione rettangolare ci permette di calcolare la base minima del pilastro. I parametri che inserisco sono:

E = modulo di elasticità

β=parametro legato ai vincoli del pilastro analizzato (in questo caso β=1)

l = lunghezza dell’elemento

Questi parametri ci permettono di calcolare il valore della snellezza e il raggio di inerzia minimo rispettivamente definite come:

λ=3,14 x (E/fyd)^0,5     e       ρmin = β x l / λ

Dopo aver calcolato il raggio di inerzia minimo posso calcolare la base minima della sezione facendo bmin=2x(3)^0,5xρmin. Ora possiamo calcolare anche l’altezza minima facendo la formula inversa hmin=A/bmin. Cosi facendo troviamo dei valori minimi che vanno ingegnerizzati. In questo caso scelgo di utilizzare una sezione 30 cm x 25 cm. 

4.d VERIFICA DELLA TRAVE E DEL PILASTRO IN LEGNO

Creo il modello del telaio su sap2000 ed oltre ai carichi qs, qp e qa aggiungo alla struttura la forza del vento Fv = 0,7 x i = 0,7 x 5 = 3,5 kN/m, e calcolo il valore delle sollecitazioni, per vedere se quest’ultima forza

influisce sulla struttura.

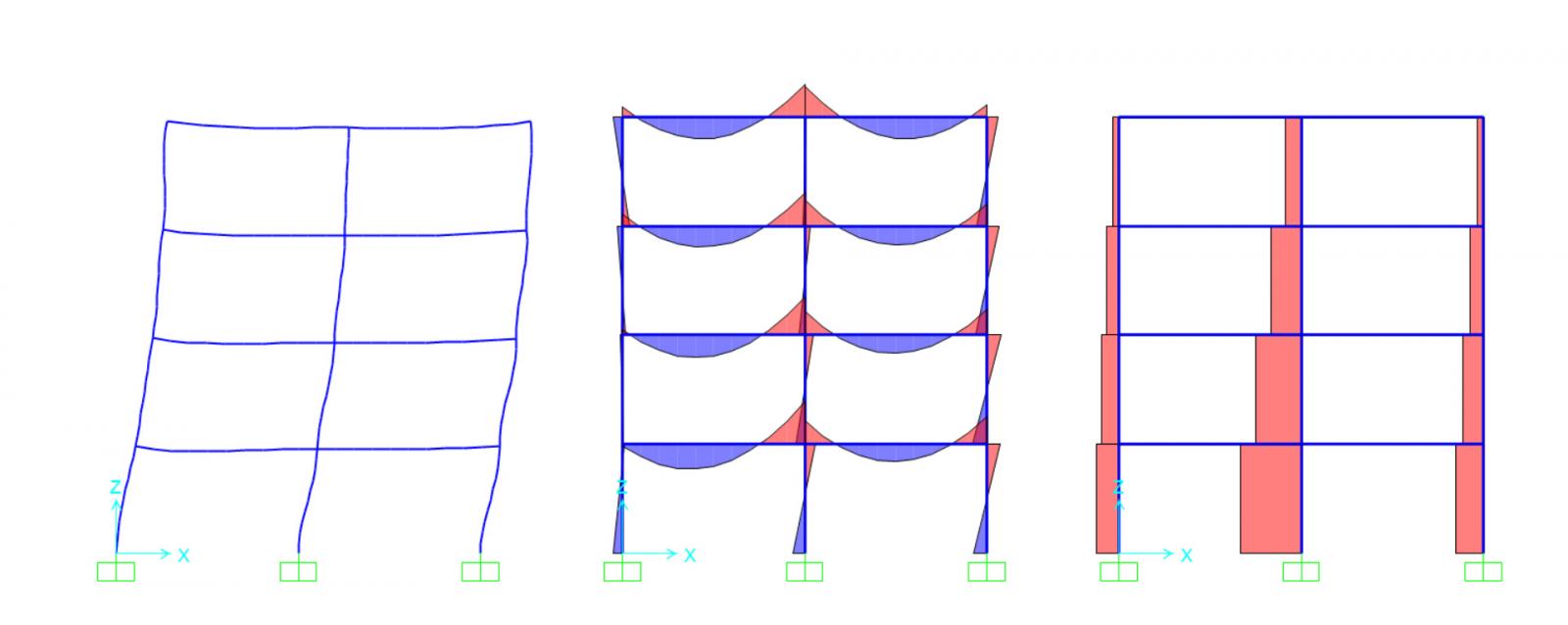
Controllo i valori sia del momento sia dello sforzo normale e verifico attraverso il foglio di calcolo se la sezione della trave e quella del pilastro che ho dimensionato sono sufficienti o dovranno essere incrementate.

 verifica Trave

  

verifica Pilastro