blog di Gianmarco.Vallorani

 

Risolvere la struttura reticolare asimmetrica

La travatura reticolare è una struttura composta da un insieme di aste complanari, vincolata ai nodi in modo da costituire un elemento resistente e indeformabile. È costituita da due elementi continui chiamati correnti, e da un’anima scomposta da elementi lineari. Gli elementi verticali vengono chiamati montanti, quelli inclinati diagonali.

Nel nostro caso ci troviamo di fronte ad una struttura reticolare asimmetrica. Le aste sono collegate tra di loro da cerniere interne. Nella verifica di questa struttura trascuriamo il peso proprio delle travi e calcoleremo solo le sollecitazioni dovute alle forze concentrate, avremmo cosi solo sforzi assiali sulle aste.

_Verifica dell’isostaticita della struttura

La struttura è isostatica se il numero dei gradi di libertà è uguale a quelli di vincolo.

L= gradi di libertà, si calcolano moltiplicando il numero delle aste per il numero dei gradi di libertà di ciascun elemento in un piano, cioè 3.

Quindi L= 11*3=33

V= gradi di vincolo, si calcolano moltiplicando i vincoli interni per quelli esterni

V=Ve+Vi        Ve=3(dovuti al carrello e alla cerniera)

Vi=2*(n-1)    n= numero delle aste

Vi    AG   n=2  2*(2-1)=2

       BDE  n=3  2*(3-1)=4

       F      n=4  2*(4-1)=6

       C      n=5  2*(5-1)=8

Vi= 2*2+4*3+6+8=30

V=3+30=33                 V=L quindi la struttura è isostatica

 

_Calcolo delle azzioni di contatto

HB+HG=0               HB=-HG----› 30kN

VB-F-F=0                 VB=20 KN

MB--› -F*1m-F*2m+HG*1m=0

HG*m=10KN*m+20KN*m---›30KN

 

_Calcolo delle azioni di contatto

Calcoliamo le forze lungo le aste con il metodo dei nodi.

Tenendo in considerazione che le aste sono soggette al solo sforzo normale possiamo procedere in 2 modi.

1-Equilibrio al nodo, scomponendo le forze che agiscono su ogni nodo e applicando le equazioni di bilancio alla traslazione orizzontale e verticale.

2-con il metodo geometrico utilizzando la regola del parallelogramma per scomporre le forze.

Nodo A

 

Il nodo è scarico

Nodo B

∑Fx=0 à30kn + N3√2/2 +N4                  N4=-30+20= -10kn

∑Fy=0 à20kn +N3√2/2 = 0                    N3= -20√2kn

 

Nodo D

L’asta 5 è scarica, l’asta 6 deve dare un carico opposto a quello dell’asta 4

 

Nodo C

∑Fx=0 àN8+N7√2/2+20   à   N8+10kn+20kn àN8=-30kn

∑Fy=0 à-10kn-N7√2/2+20kn                          àN7=10√2 kn

 

Nodo F

L’asta 11 è scarica, l’asta 9 è compressa N9=10kn

 

Nodo G

 

_Verifica della struttura con il SAP

 

 

Risolvere la struttura reticolare simmetrica

Con il metodo delle sezioni

_Verifica dell’isostaticità

V=L

L=11*3=33

V=Ve+Vi             

Vi à  BG    n=2  2*(2-1)=2

       AF    n=3  2*(3-1)=4

         CDE  n=4  2*(4-1)=6

Vi=2*2+4*2+6*3=30

Ve=3

V=3+30=33  Verificata

 

_Verifica dell’isostaticità

La trave è simmetrica quindi le reazioni vincolari sono

VB+VG+20KN+20KN+20KN  à  VB=30KN=VG

 

_Calcolare le azioni di contatto

 

Le azzioni di contatto si calcolano attraverso il sistema delle sezioni di Ritter.

La sezione di Ritter è una sezione che divide in 2 òa struttura tagliando tre aste non convergenti nello stesso nodo.

 

Sezione 1

Mc=N4*(2m)-20kn*(2m)+30kn*(4m) àN4=-40kn

MA=30kn*(2m)-N2*(2m)=0               àN2=30kn

Per calcolare N3 faccio l’equilibrio alla traslazione verticale considerando la componente verticale

30kn-20kn-N2√2/2=0   à  N3=14,14kn

 

Sezione 2

30kn+N4√2/2=0  à  N4=-42,4kn

 

Sezione 3

MD=N6*(2m)-20kn(4m)+30*(6m)  à  N6=50kn

N7√2/2+30kn-20kn=0  à  N7=-14,14kn

Sfruttando la proprietà di simmetria si possono calcolare le restanti azzioni sulle aste.

 

_Verifica della struttura con il SAP

 

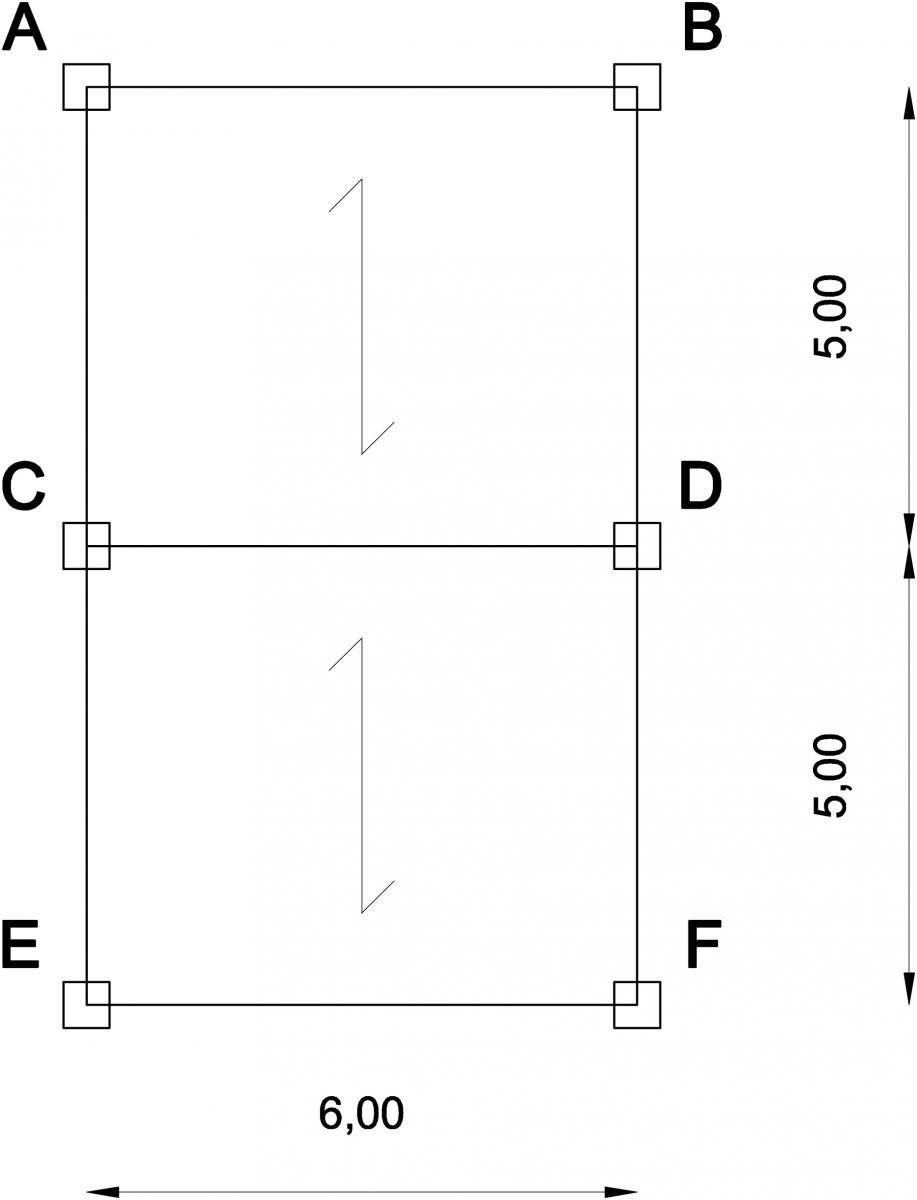
 L'esercitazione prevede il dimensionamento di una trave in tre diversi casi di materiale da costruzione: Acciaio, legno e calcestruzzo armato. Il telaio preso in considerazione, rappresenta un caso tipico nei progetti di edifici di edilizia residenziale.

In questo caso la trave maggiormente sollecitata è l'asta CD

 

_PROGETTO IN ACCIAIO

Ipotizzo un solaio in lamiera grecata, tenendo in considerazione che la lamiera grecata non raggiunge luci di una certa lunghezza, aggiungo quindi alla struttura primaria, una trave di ripartizione.

 

-Dimensionamento trave secondaria: luce:5m, interasse:2.5m, acciaio Fe235

 

Analisi dei carichi:

Qp (Azzioni permanenti non strutturali)

-Massetto (spessore 0.1m)  16.0 Kn/m³ *0.10 m = 1.6 Kn/m²

-Pavimento in pietra_______________________= 0.7 Kn/m²

-Intonaco_______________________________ = 0.3 Kn/m² 

-Impianti + divisori________________________ = 1.15 Kn/m²

-TOT________________________________ Qp = 4.10 Kn/m² 

 

Qs (Azioni permanenti, strutturali)

-Solaio in lamiera grecata A SS P600+soletta c.l.s(spessore 10cm)__ 1.90 Kn/m²

-TOT_________________________________Qs = 1.90 Kn/m²

 

Qa (Carichi accidentali)

-Categoria A____________________________Qa =  2.00 Kn/m² 

q = (Qp+Qs+Qa) * interasse = (4.1+1.90+2.00)Kn/m²  * 3m =  24.00 Kn/m

Dal modulo elettronico di excel ottengo Wx=335 cm³

Quindi scelgo dal sagomario un Ipe 270 con Wx=428.87 cm³

A questo punto aggiungo il peso del travetto al ml a q 

Qs+p.proprio trave* 1m= 1.90 Kn/m² + 0.36 Kn/m² = 2.26 Kn/m²

  

-Dimensionamento trave principale: Luce:6.00 m, Interasse: 2.5m, Acciaio Fe235

Procedo con il dimensionamento della trave principale mantenendo il valore dei carichi di solaio aggiungendo al valore Qs il peso proprio della trave secondaria

Qs+p.proprio trave = 2.26 Kn/m²

Con il foglio elettronico mi calcolo im modulo di resistenza minimo Wx

Ottengo un WX=420 cm³ 

Scelgo dal sagomario un Ipe 300 con Wx=557 cm³

Avendo scelto un Wx molto piu alto di quello di progetto, non procedo alla verifica aggiungendo il peso proprio della nuova trave, in quanto sarà di certo verificato

 

_PROGETTO IN LEGNO

 

Analisi dei carichi:

 

Qp (Azzioni permanenti non strutturali)

-Tavolato (spessore 0.04 m) 0.4 Kn/m³ *0.04 m___________= 0.16 Kn/m²

-Massetto cementizio (spessore 0.05 m) 18.00 Kn/m³ *0.05m = 0.9 Kn/m²

-Allettamento (spessore 1 cm)_________________________ = 0.16 Kn/m² 

-Pavimento in mattonelle di cemento____________________ = 0.18 Kn/m²

-Impianti + Divisori___________________________= 1.5 Kn/m²

 

-TOT________________________________ Qp = 2.9 Kn/m² 

 

Qa (Carichi accidentali)

-Categoria A____________________________Qa =  2.00 Kn/m²  

-Dimensionamento trave secondaria: luce:5m, interasse:1m 

Inserendo i valore nel foglio di calcolo Excel, imposto una base della trave di 18 cm

Ottengo un hmin= 23.96 cm

Dalla tabella scelgo una sezione di 18x28 cm a favore di sicurezza

Aggiungo al calcolo il peso proprio della trave e faccio il calcolo di verifica con il foglio elettronico

Qs = 7.00 Kn/m³ * 0.045 m² =0.31 Kn/m 

 

Ho un valore di hmin = 24.71 cm inferiore a quello di progetto quindi la sezione 18x28 cm è verificata

-Dimensionamento trave principale: Luce:6.00 m, Interasse: 2.5m

Per l'analisi dei carichi, aggiungo al carico Qs il peso proprio delle travi secondarie

Nuovamente con il foglio elettronico inserisco i dati prendendo questa volta una base di 30cm

ottengo un hmin = 51.36 cm

come fattore di sicurezza prendo una sezione 30x52 cm

e aggiungo il peso della trave al mq a q e faccio la verifica con la medesima procedura

Dai dati del foglio elettronico di Excel risulta che la trave non è verificata quindi scego una trave piu grande : 40x60 cm procedo nuovamente con la verifica con la verifica

In questo caso la sezione risulta verificata

 

_PROGETTO IN C.l.s armato

 

-Dimensionamento trave principale: Luce:6.00 m, interasse:5.00m

acciaio B450C cls C40/50 

 

 

Analisi dei carichi:

 

Qp (Azzioni permanenti non strutturali)

 

-Pavimento_________________________________= 0.10 Kn/m²

-Isolante (spessore 0.01 m) 7.00 Kn/m³ *0.01m____ = 0.07 Kn/m²

-Intonaco (spessore 0.015 m) 10.00 Kn/m³ *0.015m = 0.15 Kn/m²  

-Impianti + Divisori___________________________= 1.5 Kn/m²

-TOT________________________________ Qp = 2.6 Kn/m² 

 

 

Qa (Carichi accidentali)

-Categoria A____________________________Qa =  2.00 Kn/m² 

 

Qs (Azioni permanenti, strutturali)

-Pacchetto solaio H.20 cm___________________ 2.66 Kn/m²

Inserisco i dati nel foglio Excel scegliendo una base di 25 cm

ottengo un'altezza di 36.17 cm, come fattore di sicurezza scelgo una sezione piu grande di 42cm

aggiungo cosi il peso proprio della trave al foglio di calcolo in modo da ottenere la verifica

 

La trave risulta verificata in quanto l'Hmin di verifica è minore dell'H di progetto