Esercitazione travi reticolari
Risolvere la struttura reticolare asimmetrica
La travatura reticolare è una struttura composta da un insieme di aste complanari, vincolata ai nodi in modo da costituire un elemento resistente e indeformabile. È costituita da due elementi continui chiamati correnti, e da un’anima scomposta da elementi lineari. Gli elementi verticali vengono chiamati montanti, quelli inclinati diagonali.
Nel nostro caso ci troviamo di fronte ad una struttura reticolare asimmetrica. Le aste sono collegate tra di loro da cerniere interne. Nella verifica di questa struttura trascuriamo il peso proprio delle travi e calcoleremo solo le sollecitazioni dovute alle forze concentrate, avremmo cosi solo sforzi assiali sulle aste.
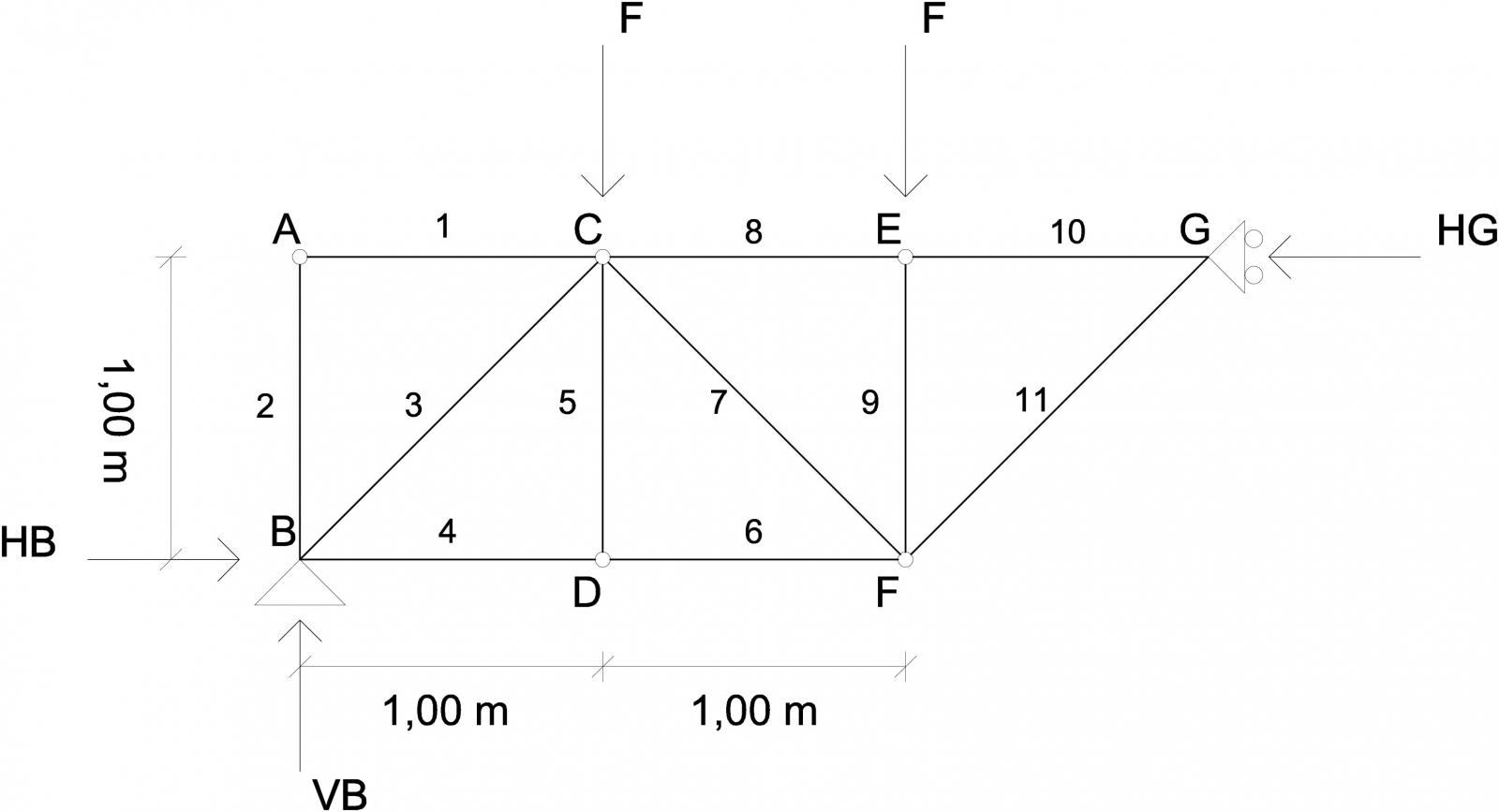
_Verifica dell’isostaticita della struttura
La struttura è isostatica se il numero dei gradi di libertà è uguale a quelli di vincolo.
L= gradi di libertà, si calcolano moltiplicando il numero delle aste per il numero dei gradi di libertà di ciascun elemento in un piano, cioè 3.
Quindi L= 11*3=33
V= gradi di vincolo, si calcolano moltiplicando i vincoli interni per quelli esterni
V=Ve+Vi Ve=3(dovuti al carrello e alla cerniera)
Vi=2*(n-1) n= numero delle aste
Vi AG n=2 2*(2-1)=2
BDE n=3 2*(3-1)=4
F n=4 2*(4-1)=6
C n=5 2*(5-1)=8
Vi= 2*2+4*3+6+8=30
V=3+30=33 V=L quindi la struttura è isostatica
_Calcolo delle azzioni di contatto
HB+HG=0 HB=-HG----› 30kN
VB-F-F=0 VB=20 KN
MB--› -F*1m-F*2m+HG*1m=0
HG*m=10KN*m+20KN*m---›30KN
_Calcolo delle azioni di contatto
Calcoliamo le forze lungo le aste con il metodo dei nodi.
Tenendo in considerazione che le aste sono soggette al solo sforzo normale possiamo procedere in 2 modi.
1-Equilibrio al nodo, scomponendo le forze che agiscono su ogni nodo e applicando le equazioni di bilancio alla traslazione orizzontale e verticale.
2-con il metodo geometrico utilizzando la regola del parallelogramma per scomporre le forze.
Nodo A
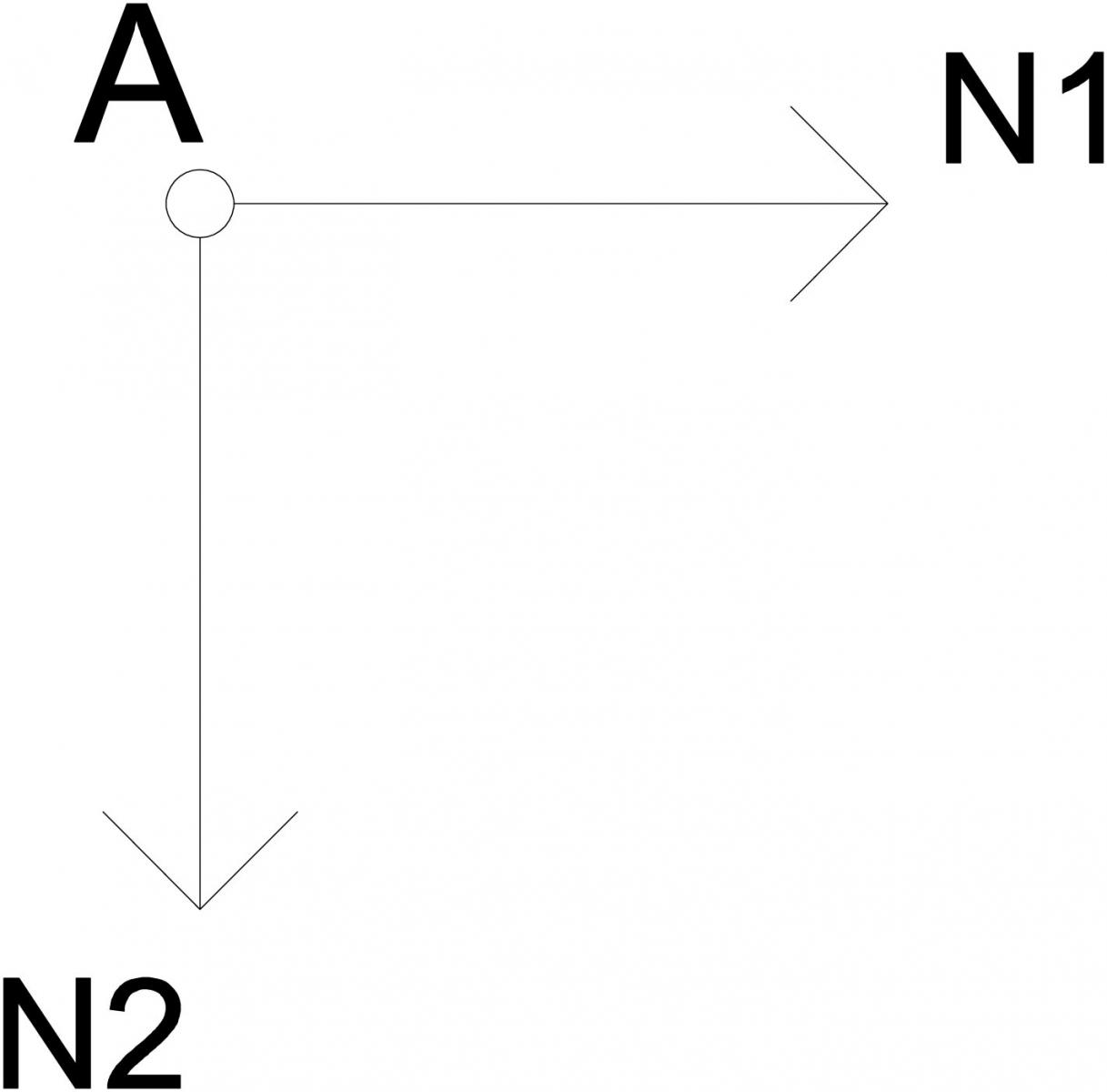
Il nodo è scarico
Nodo B
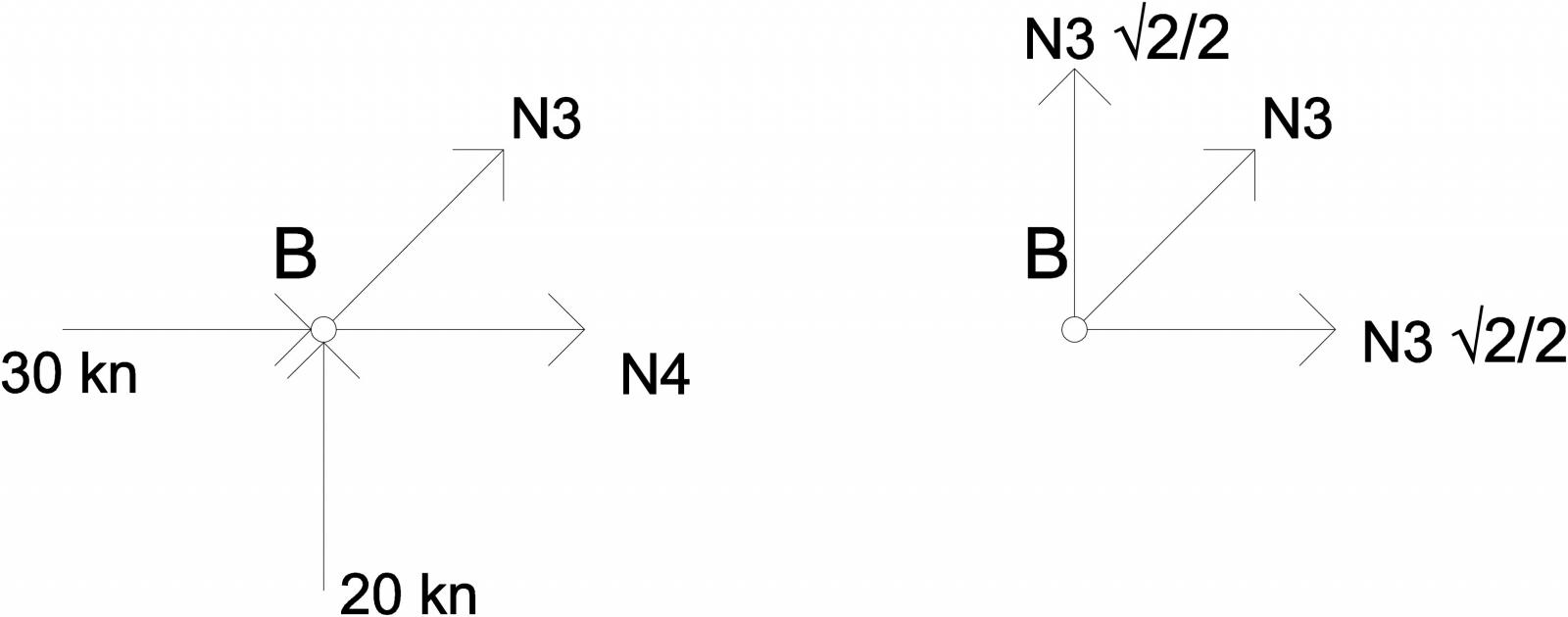
∑Fx=0 à30kn + N3√2/2 +N4 N4=-30+20= -10kn
∑Fy=0 à20kn +N3√2/2 = 0 N3= -20√2kn
Nodo D
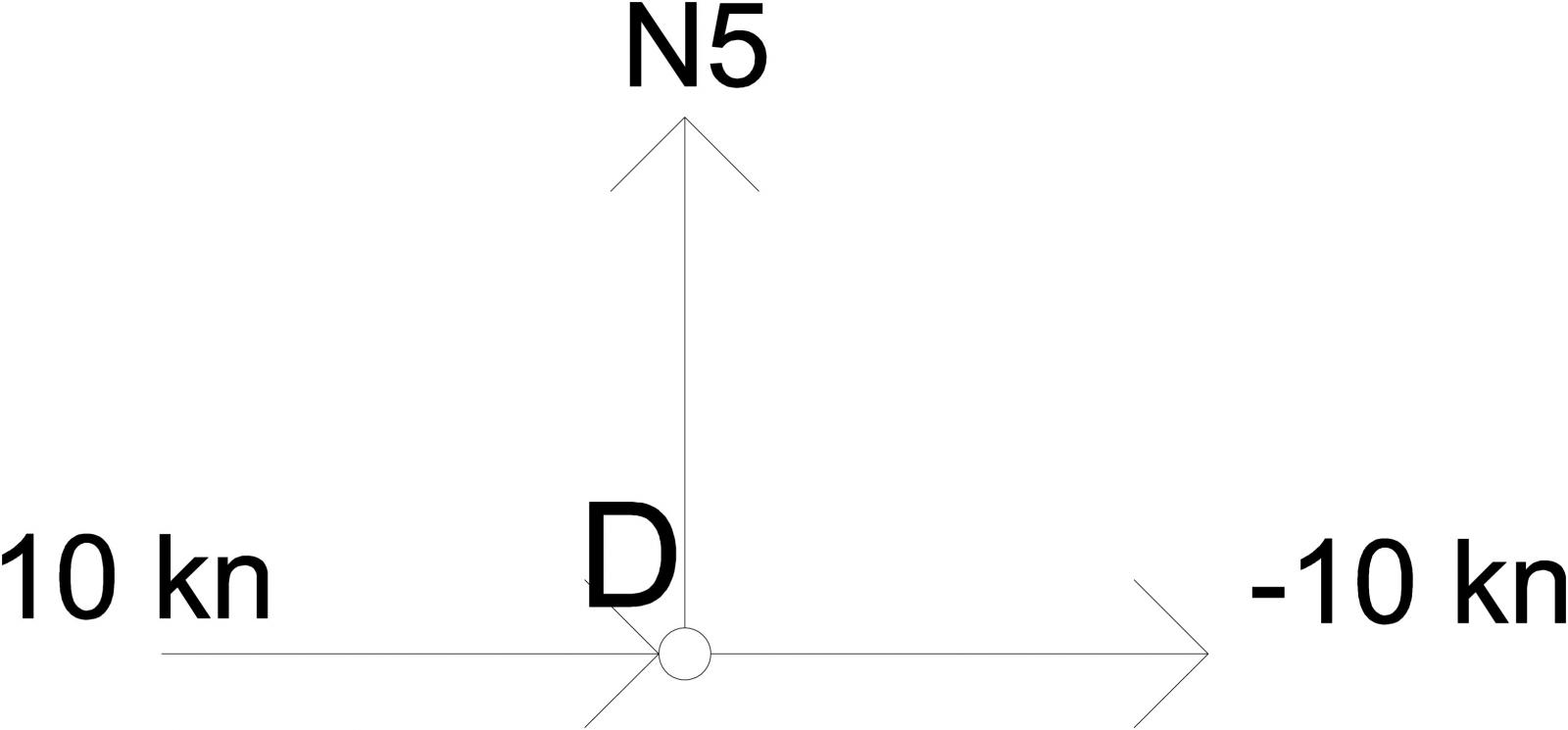
L’asta 5 è scarica, l’asta 6 deve dare un carico opposto a quello dell’asta 4
Nodo C
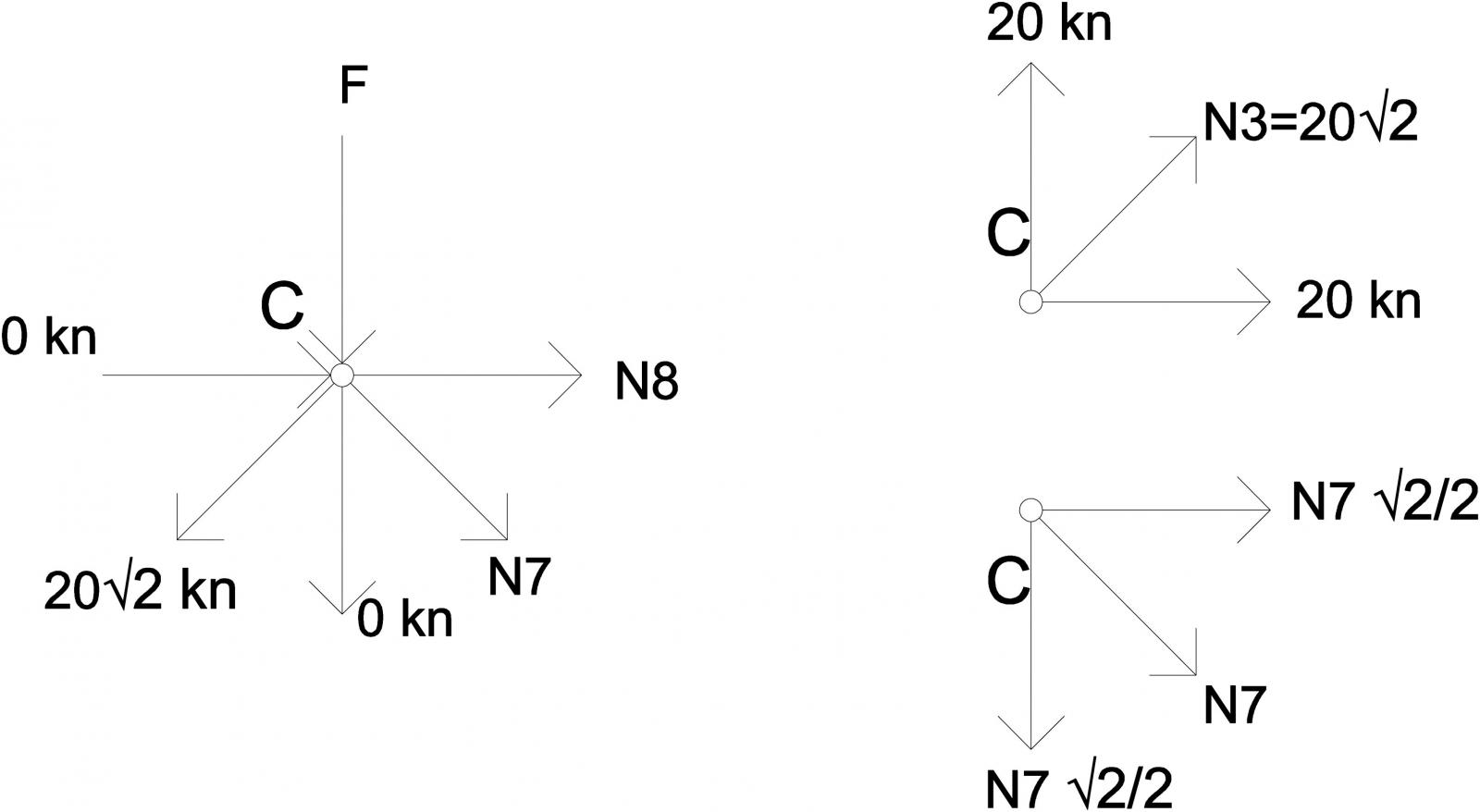
∑Fx=0 àN8+N7√2/2+20 à N8+10kn+20kn àN8=-30kn
∑Fy=0 à-10kn-N7√2/2+20kn àN7=10√2 kn
Nodo F
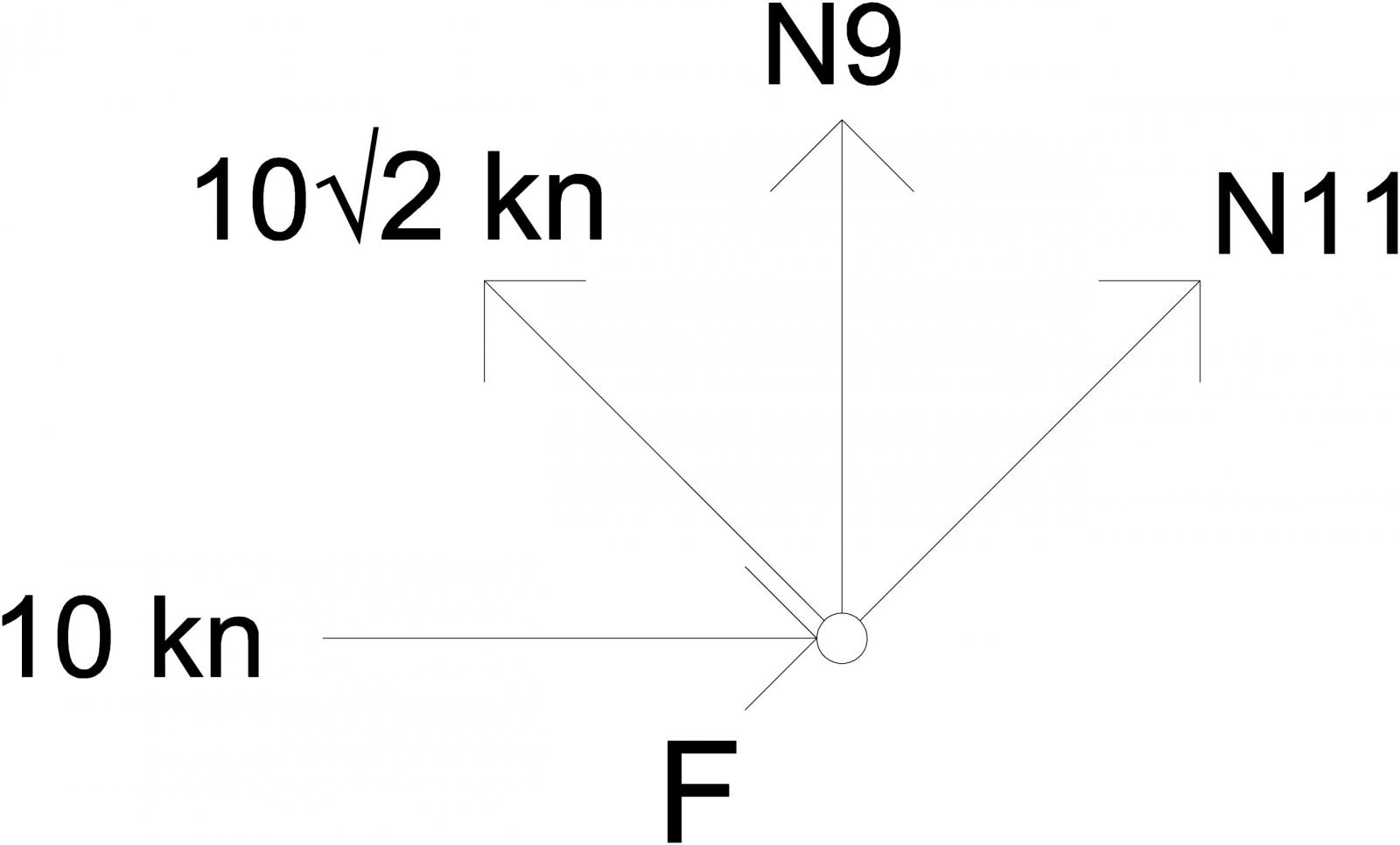
L’asta 11 è scarica, l’asta 9 è compressa N9=10kn
Nodo G

_Verifica della struttura con il SAP
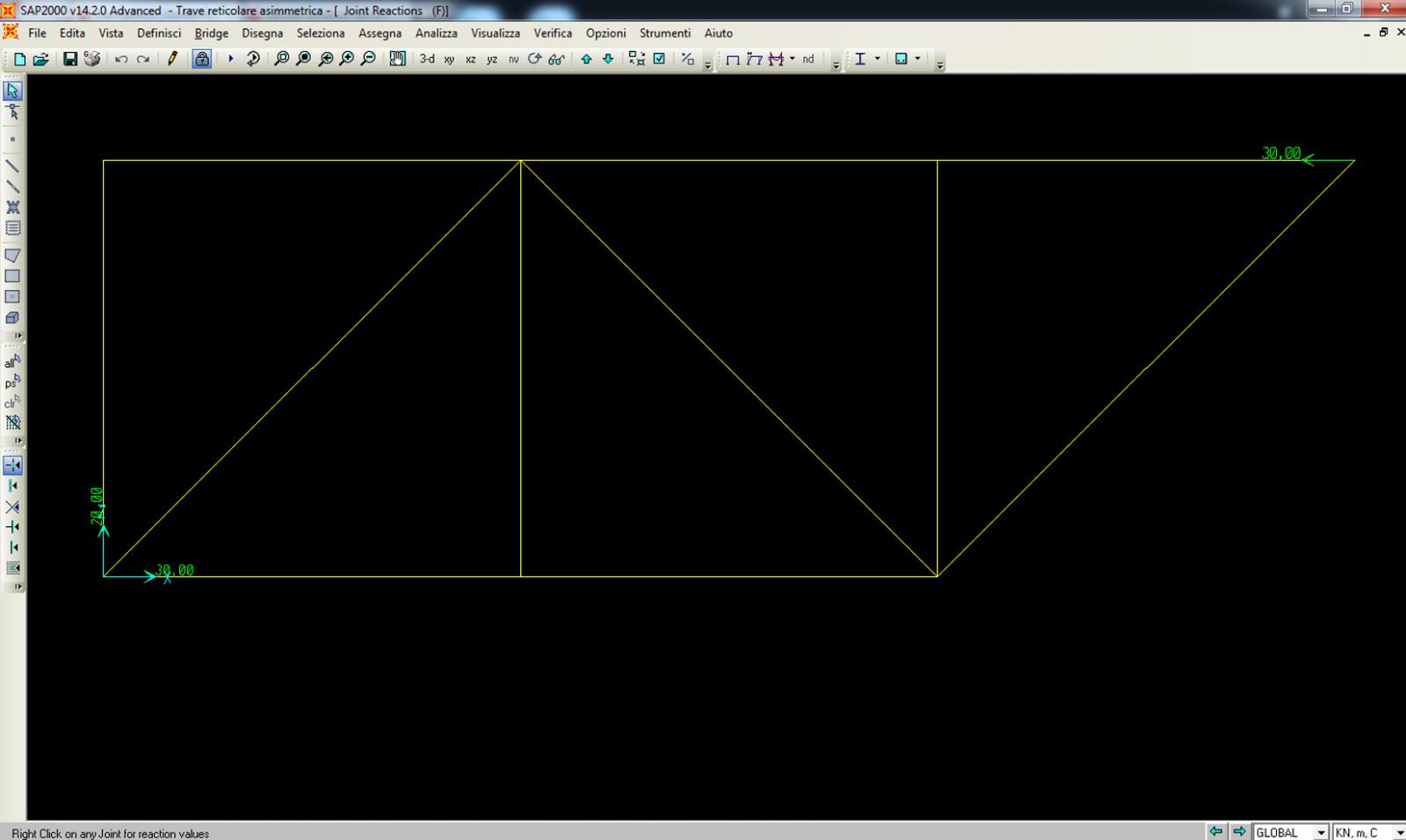
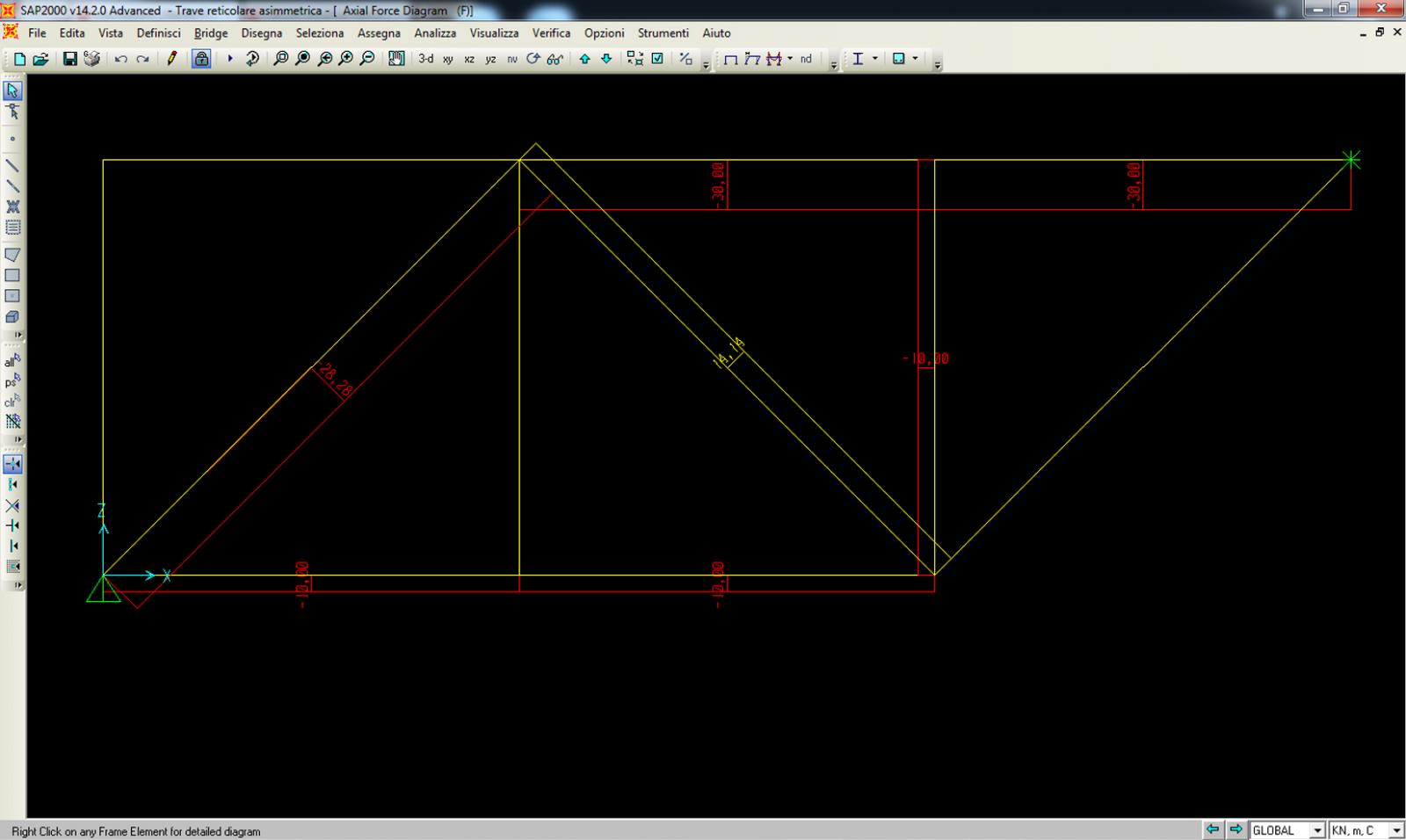
Risolvere la struttura reticolare simmetrica
Con il metodo delle sezioni
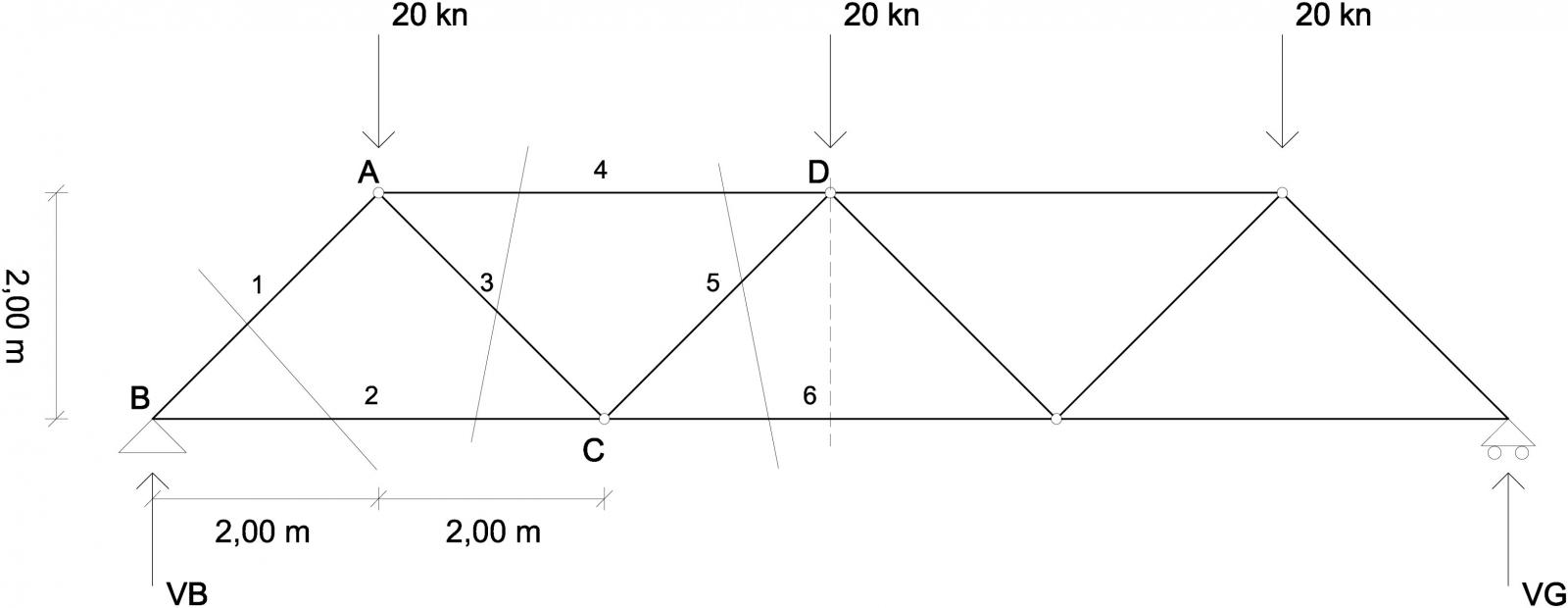
_Verifica dell’isostaticità
V=L
L=11*3=33
V=Ve+Vi
Vi à BG n=2 2*(2-1)=2
AF n=3 2*(3-1)=4
CDE n=4 2*(4-1)=6
Vi=2*2+4*2+6*3=30
Ve=3
V=3+30=33 Verificata
_Verifica dell’isostaticità
La trave è simmetrica quindi le reazioni vincolari sono
VB+VG+20KN+20KN+20KN à VB=30KN=VG
_Calcolare le azioni di contatto
Le azzioni di contatto si calcolano attraverso il sistema delle sezioni di Ritter.
La sezione di Ritter è una sezione che divide in 2 òa struttura tagliando tre aste non convergenti nello stesso nodo.
Sezione 1
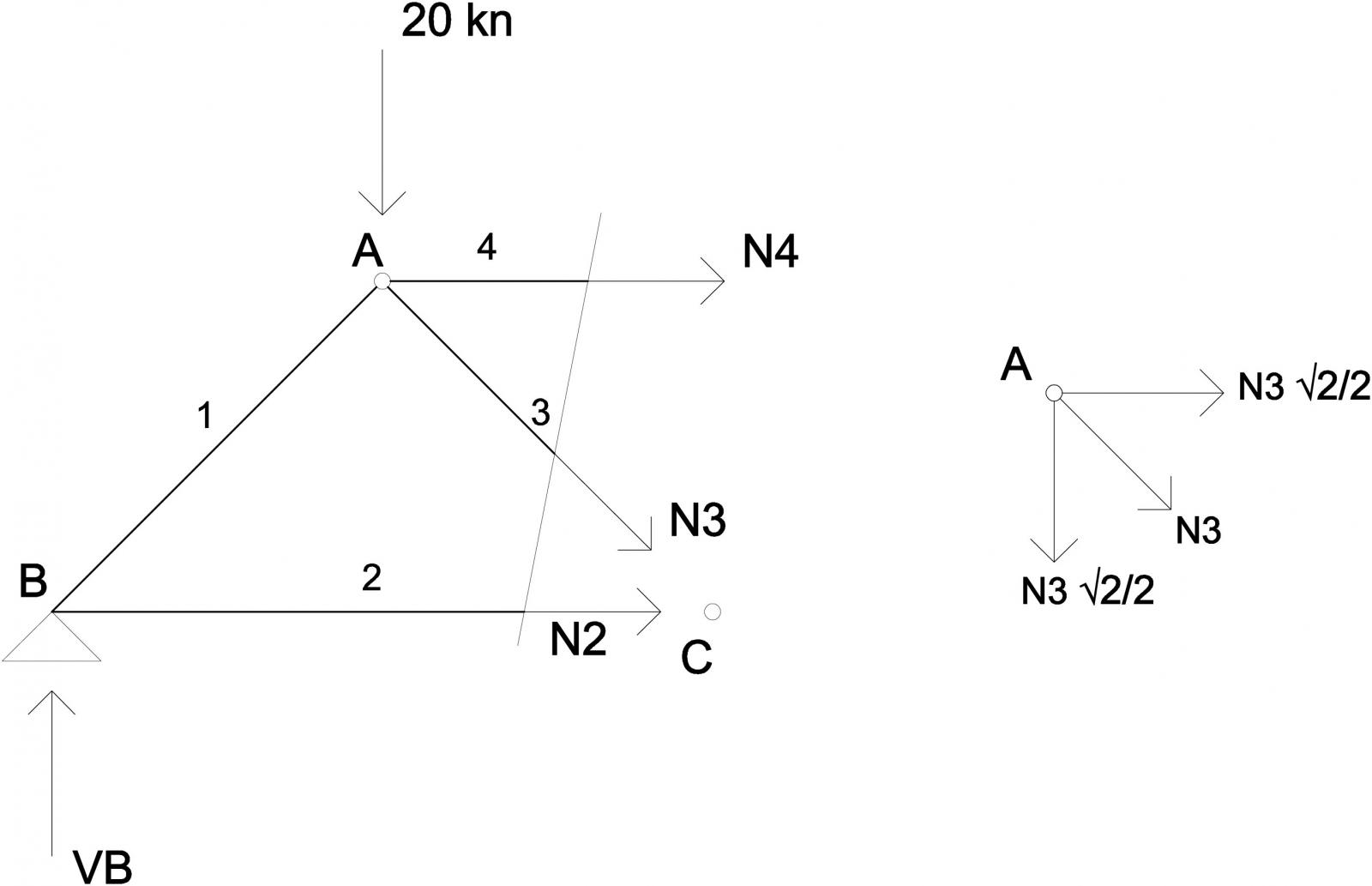
Mc=N4*(2m)-20kn*(2m)+30kn*(4m) àN4=-40kn
MA=30kn*(2m)-N2*(2m)=0 àN2=30kn
Per calcolare N3 faccio l’equilibrio alla traslazione verticale considerando la componente verticale
30kn-20kn-N2√2/2=0 à N3=14,14kn
Sezione 2
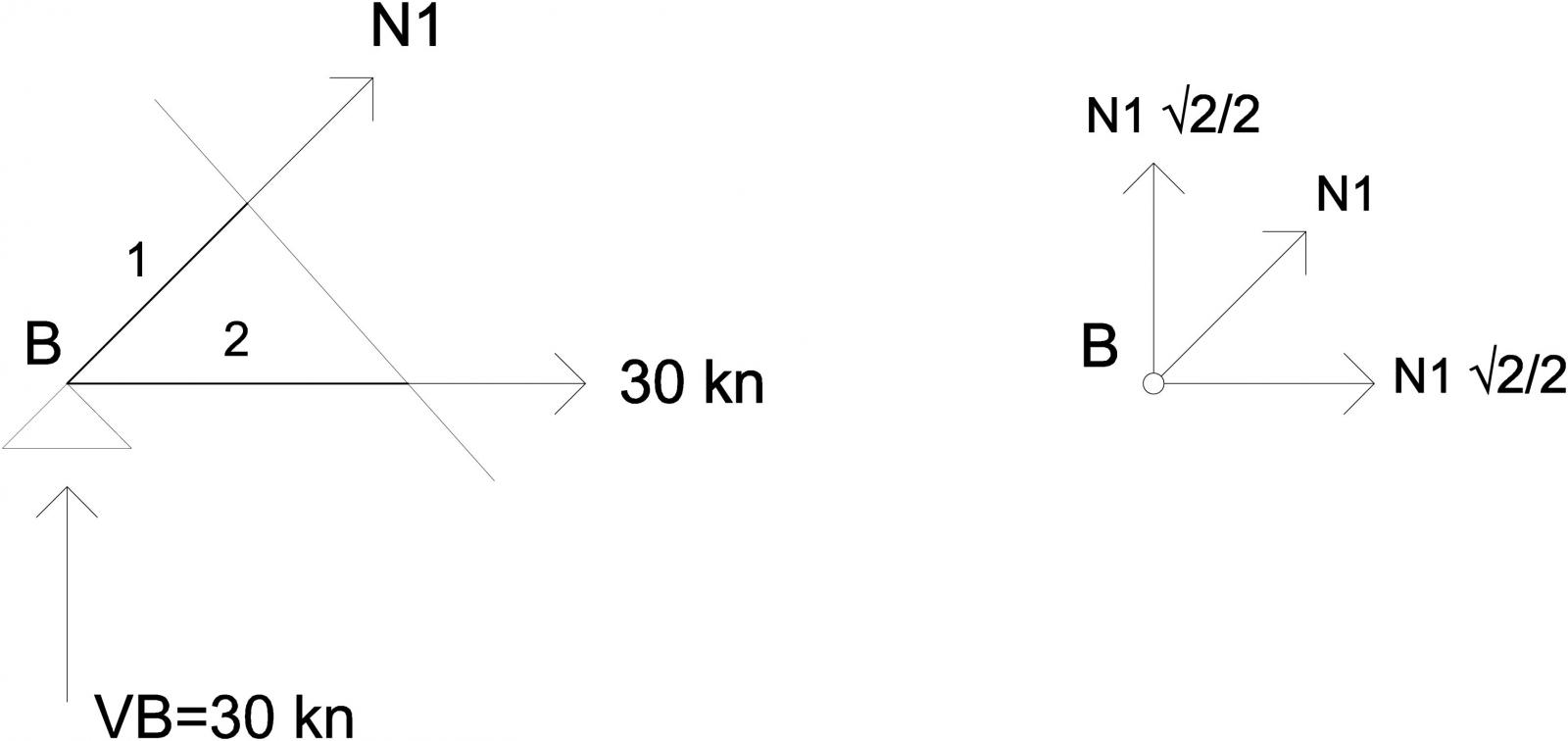
30kn+N4√2/2=0 à N4=-42,4kn
Sezione 3

MD=N6*(2m)-20kn(4m)+30*(6m) à N6=50kn
N7√2/2+30kn-20kn=0 à N7=-14,14kn
Sfruttando la proprietà di simmetria si possono calcolare le restanti azzioni sulle aste.
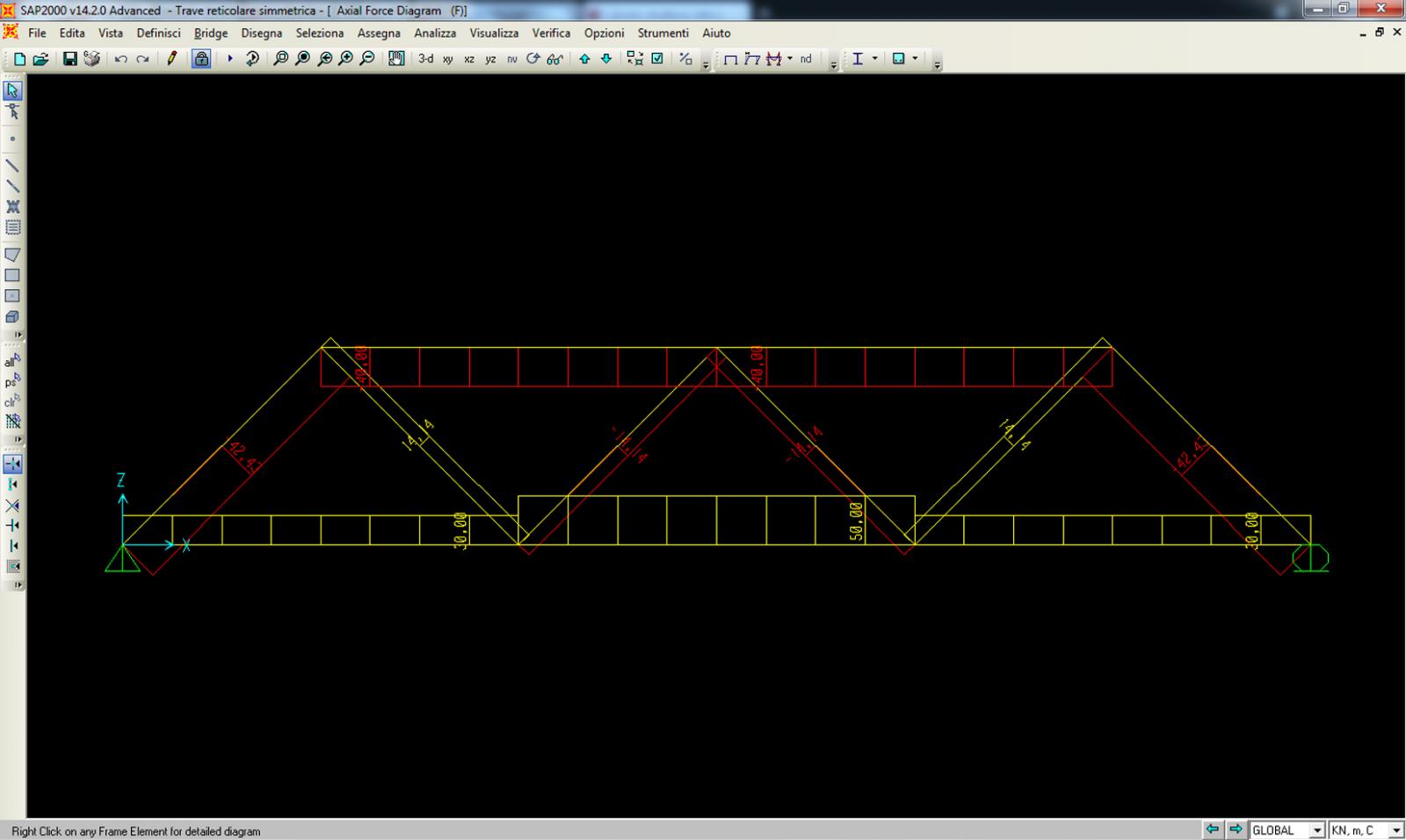
_Verifica della struttura con il SAP
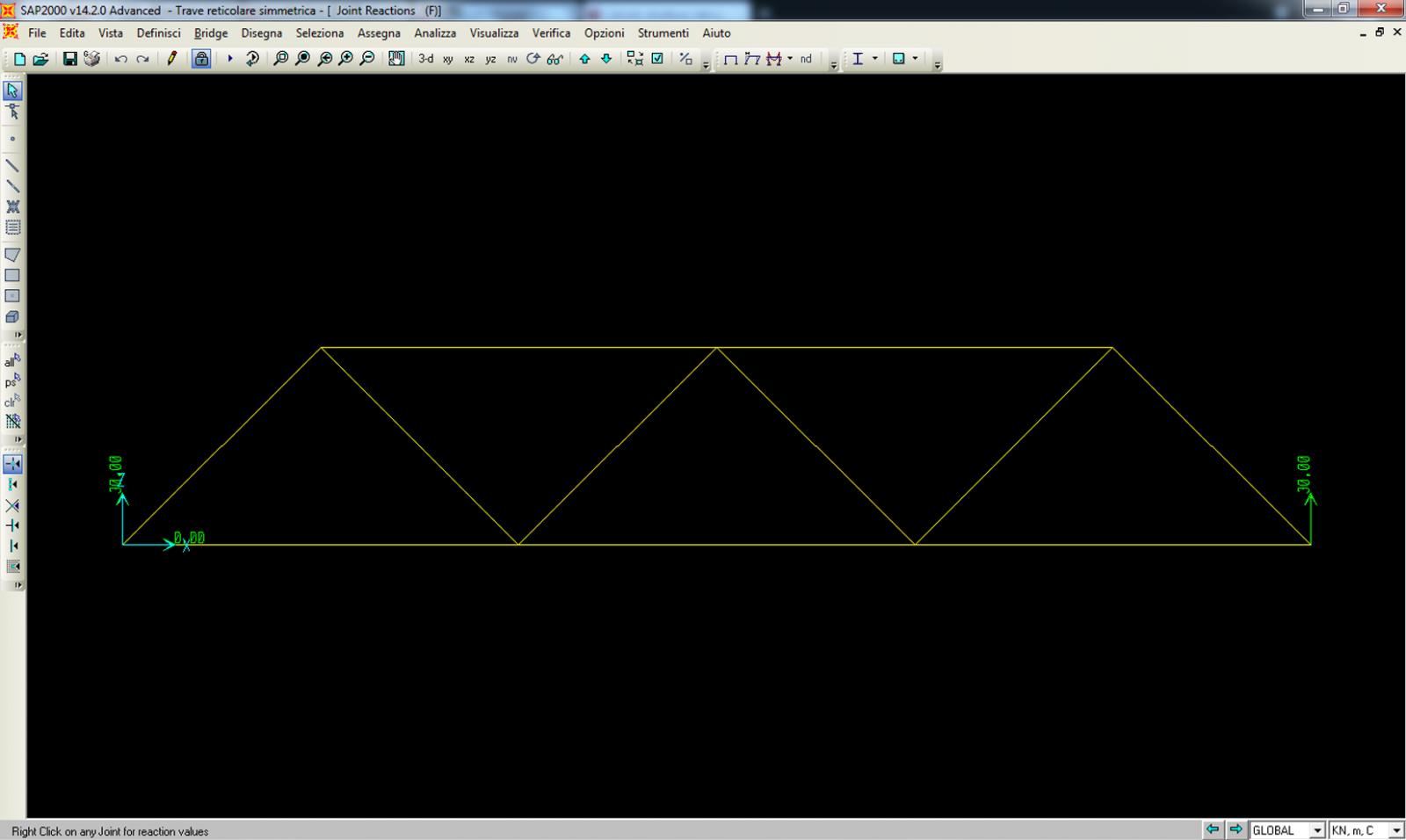

Commenti recenti