blog di carlotta.iachella

La seconda parte dell’esercitazione consiste nell’inserimento in SAP della struttura precedentemente dimensionata, e di verificare le sezioni con i dati forniti dal software. Anche in questo caso si prenderanno in considerazione due tipi di strutture diverse realizzate in tre materiali diversi: legno, calcestruzzo e acciaio

Struttura in calcestruzzo

Si è iniziato disegnando lo schema strutturale in SAP2000 di tutti gli elementi del piano terra che poi sono stati duplicati in altezza; ogni elemento è stato disegnato come un frame separato in modo da andare a generare dei nodi rigidi, vincolando alla fine i pilastri del piano terra con degli incastri al suolo. Si è quindi passati alla definizione del materiale e delle sezioni come definite dall’esercitazione.

A questo punto si è passati all’inserimento dei carichi distribuiti lungo le travi principali. Nel calcolo strutturale questi sono stati combinati tra loro attraverso la SLU alla quale poi sono state aggiunte in seguito anche le forze orizzontali dovute dal vento e dal sisma.

Sono state estrapolate le tabelle delle sollecitazioni di ogni singolo gruppo di elementi. Dalla tabella excel si cerca il valore massimo del momento sia per le travi primarie che per le secondarie e gli sbalzi. Per le travi il momento massimo trovato risulta essere comunque più basso rispetto a quello calcolato in precedenza, questo perché nel nodo rigido il momento è passate, e quindi diverso da zero, permettendo di avere una sollecitazione in mezzeria sensibilmente minore. Provando a eseguire il dimensionamento con il nuovo valore del momento, si è potuto constatare che la sezione scelta precedentemente era adeguata e per questo è stata mantenuta.

Lo stesso procedimento è stato svolto per il calcolo della trave secondaria, in questo caso il momento risultava essere molto più basso rispetto a quello della primaria. La si è comunque dimensionata leggermente più grande rispetto ai valore calcolato.

Per quanto riguarda lo sbalzo, anche in questo caso si è svolta nuovamente l’operazione di ridimensionamento e verifica all’abbassamento come svolto nella parte dell’esercitazione precedente; l'elemento è stato ottimizzato poiché era risultato sovradimensionato nella prima parte dell'esercitazione.

Per quanto riguarda il pilastro si è proceduto attraverso il dimensionamento e la verifica a snellezza della sezione prendendo in considerazione lo sforzo assiale agente mediante i calcoli svolti in precedenza. I pilastri sono stati poi verificati a pressoflessione in un secondo momento.

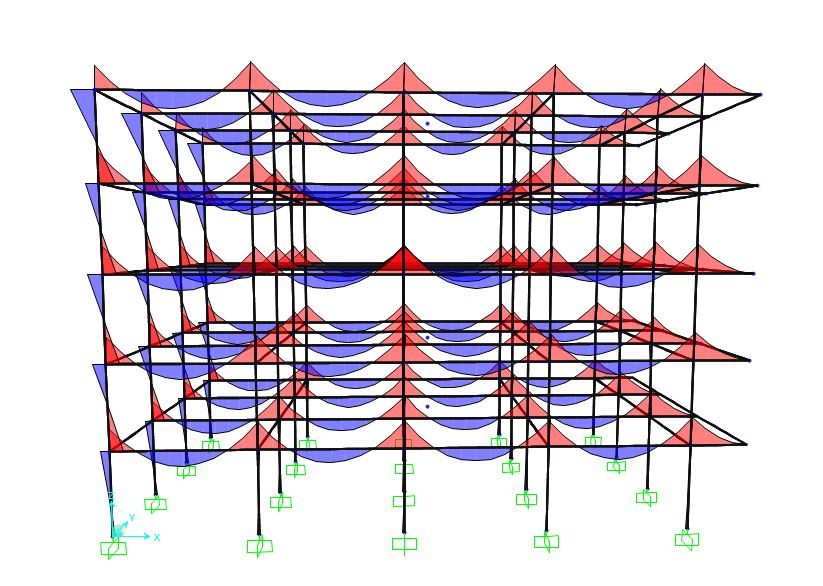
Trave principale

Trave secondaria

Sbalzo

Pilastro

Carico neve

Una volta definite le sezioni di tutti e quattro gli elementi, si è continuato attraverso la verifica degli elementi nel caso in cui questi siano sottoposti ad un carico maggiorato dal peso della neve. La maggiorazione dipende da moltissimi fattori quali la zona climatica in cui si trova l’edificio sottoposto al calcolo, la tipologia del tetto, la sua inclinazione, la possibilità di essere o meno riscaldato e altri.
Nel mostro caso abbiamo ipotizzato un peso di circa 0,5 kN/m², dovuto al fatto che ci si trovi a Roma, con una tipologia edilizia comunque a questa zona. Il peso è stato poi moltiplicato anch’esso per l’interasse di 4m, in modo da trovarci un carico utilizzabile in SAP di 2 kN/m e collocato sul solaio di copertura. Ipotizzando che nei 0,5kN/m² fosse già presente il coefficiente di sicurezza, abbiamo quindi operato un calcolo alla SLU + neve, verificando che gli sforzi negli elementi maggiormente sollecitati non aumentano in modo eccessivo, e che quindi le sezioni calcolate alla SLU erano verificate anche per il carico neve.

A questo punto si è passati alla verifica degli elementi verticali alle spinte orizzontali. Durante la vita di un edificio sebbene i carichi “principali” risultino essere quelli verticali, vi è una parte di forze orizzontali quali il vento e la forza sismica, che investono la struttura in maniera orizzontale. E’ quindi necessario verificare gli elementi verticali a queste forze, in quanto risultano essere quelli più sollecitati. Sia per il vento che per il sisma non siamo in grado di sapere quale sia la direzione precisa con cui investiranno la struttura, per questo motivo andremo a svolgerci un’analisi sia per la direzione in x, sia per la direzione in y, verificheremo per quale delle due i nostri elementi saranno più sollecitati e svolgeremo il dimensionamento.

Spinta del vento

A questo punto si è passati alla verifica degli elementi verticali alle spinte orizzontali. Sia per il vento che per il sisma non siamo in grado di sapere quale sia la direzione precisa con cui investiranno la struttura, per questo motivo andremo a svolgerci un’analisi sia per la direzione in x, sia per la direzione in y, verificheremo per quale delle due i nostri elementi saranno più sollecitati e svolgeremo il dimensionamento.

Il vento è considerato un agente dinamico, e quindi che varia di intensità e direzione nel tempo. Per questo motivo si è scelto di semplificare il caso preso in esame ipotizzando il vento come un agente statico, che imprimesse un carico distribuito differente sui pilastri posti in pressione e depressione. Dall’analisi allegata di seguito, si è deciso di prendere in considerazione solo il momento sui pilastri nella direzione x, in quanto risulta essere quella che maggiormente stressa il pilastro a flessione e compressione.

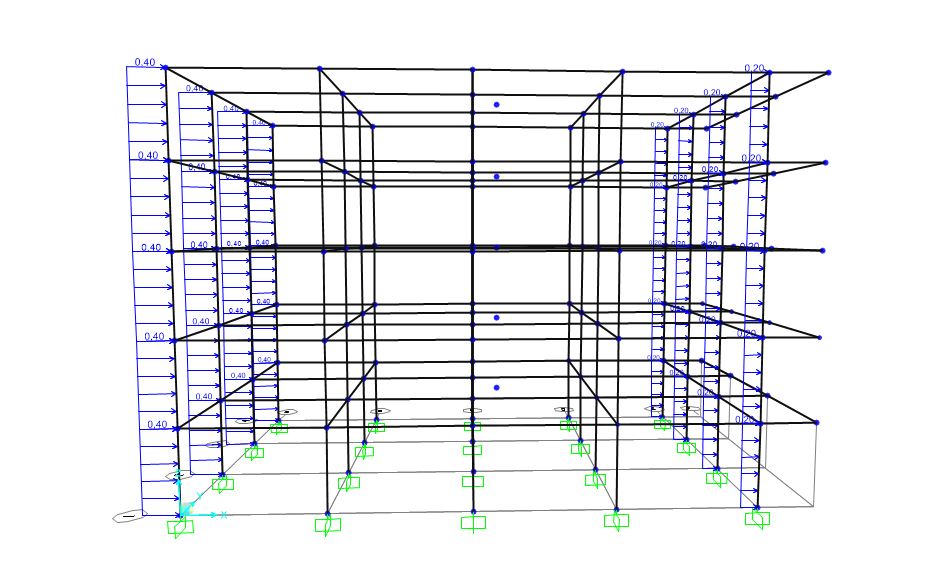
Spinta sismica

La forza sismica che investe un edificio è caratterizzata da due grandezze principali: l’accelerazione, calcolata dall’energia che ci si aspetta venga sprigionata durante il sisma e che dipende dalla zona dove ci si trova espressa in una frazione di g, e la massa, e quindi il peso, dell’edificio. Sapendo che la forza sismica non si distribuisce verticalmente in maniera costante lungo tutto l'edificio (e quindi aumenta con il salire degli impalcati), ci si è calcolati la forza concentrata nel centro d’area di ogni impalcato come semplificazione dell'azione sismica. Anche in questo caso si è svolta prima la verifica lungo la direzione x, e poi lungo quella y, andando poi a constatare che anche in questo caso gli elementi risultavano più sollecitati se investiti da una forza proveniente dalla direzione x. 

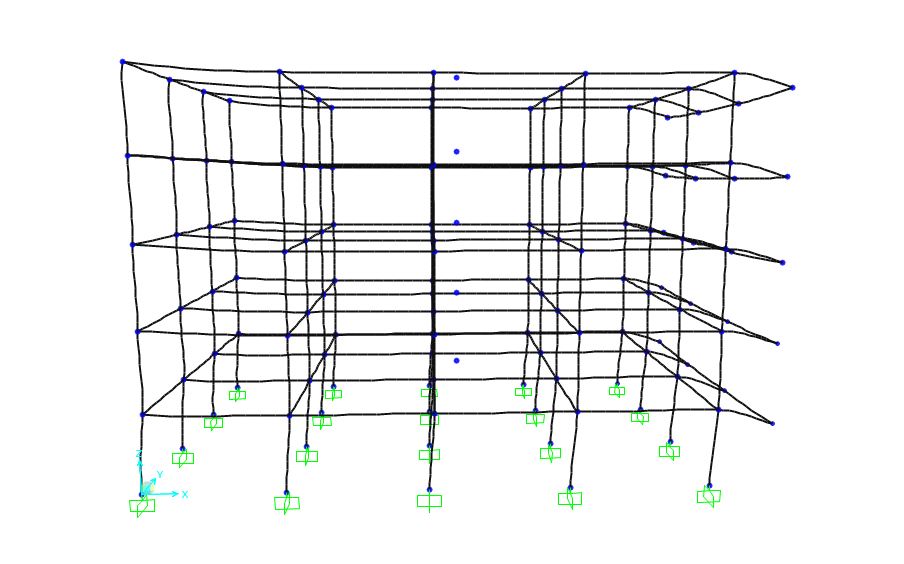
TELAIO IN LEGNO

Per quanto riguarda il dimensionamento e la verifica del telaio in Legno su SAP2000, è stata impiegata la medesima struttura elaborata per il calcestruzzo armato (dato che queste due erano geometricamente identiche), agendo su materiali e sezioni degli elementi. I carichi definiti per i solai e la destinazione d’uso nella prima parte dell’esercitazione sono stati ripartiti sulle travi principali, facendo riferimento alla fascia di spettanza di queste. È stato quindi definito un nuovo materiale legno lamellare riportando i parametri impiegati precedentemente sul programma.

Il passo successivo è stato quello di andare a verificare il pre-dimensionamento degli elementi riportati sul programma rispetto allo SLU, questa volta facendo anche riferimento al carico distribuito della neve. Dall’analisi è conseguito che la prima ingegnerizzazione  delle travi principali  risultava essere leggermente sovradimensionata; la sezione è stata leggermente ridotta rispetto alla nuova analisi. La trave secondaria è stata dimensionata secondo lo stesso iter della principale, rispetto al momento flettente massimo estrapolato da SAP2000, ma l’altezza minima era così piccola che si è deciso di portare la sezione a un’altezza uguale a quella della principale. Per ciò che riguarda lo sbalzo, per quanto il momento flettente ricavato dall’analisi su SAP2000 fosse leggermente più alto, la differenza era così piccola che la sezione è rimasta la stessa rispetto a quella pre-dimensionata. Anche nel caso del pilastro ci si è trovati nella situazione di non dover alterare il pre-dimensionamento in quanto lo sforzo assiale ottenuto dall’analisi mediante il programma non influiva in modo marcato sul nuovo progetto della sezione.

Trave principale

Trave secondaria

Sbalzo

Pilastro

Spinta del vento

Una volta assegnate le nuove sezioni ingegnerizzate sul telaio elaborato in SAP2000 si è passati ad effettuare una verifica della struttura rispetto all’azione del vento. In particolare, avendo notato già rispetto al caso del calcestruzzo armato che la direzione più sollecitata era quella X (la direzione parallela al lato lungo dell’edificio)  si è deciso di eseguire solamente tale verifica. Dall’analisi rispetto a questo carico orizzontale è stata estrapolata una tabella relativa alle sollecitazioni assiali e ai momenti agenti su tutti i pilastri; su di essa è stata fatta una verifica a pressoflessione progettando un foglio excel per calcolare le tensioni assiali e flessionali di ogni pilastro e controllare che la somma dei rapporti fra queste e le relative resistenze di progetto (parallele alla fibra e a flessione) fossero minori o uguali a 1. L’esito della verifica è stato positivo, quindi non è stato necessario tornare sul dimensionamento degli elementi.

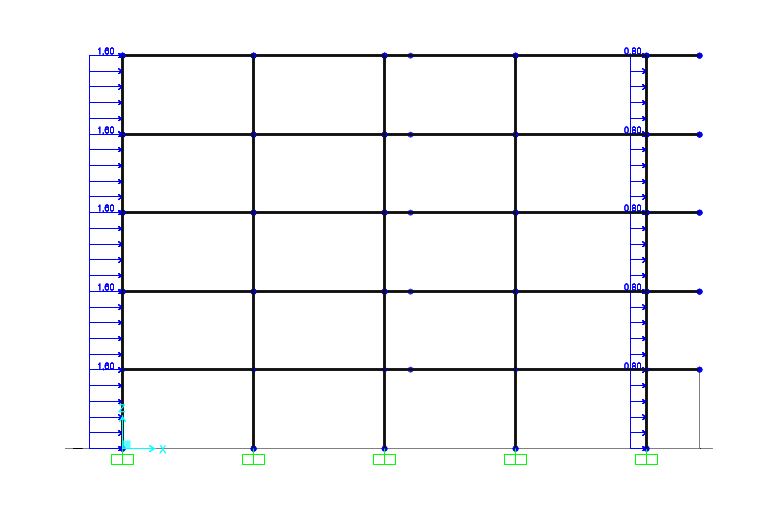
Spinta sismica

Si è effettuato infine un’analisi sul telaio rispetto all’azione sismica (sempre in direzione X, la direzione più sollecitata come riscontrato in precedenza), andando a calcolare per ogni impalcato quale fosse la forza sismica agente e attribuendo quest’ultima come carico concentrato nel centro d’area di ogni singolo piano. La verifica è risultata anche in questo caso positiva, per cui le sezioni ingegnerizzate sono state mantenute come tali.

TELAIO IN ACCIAIO

Per il dimensionamento e la verifica del telaio in Acciaio si è iniziato modificando la struttura precedentemente utilizzata, per l’analisi dei telai in legno e calcestruzzo, al fine di renderla coerente con l’ipotesi di progetto effettuata nella prima parte dell’esercitazione. Oltre a modificare le dimensioni della struttura sono stati modificati anche i carichi su di essa agenti.

Il passo successivo è stato (come nel caso del telaio in legno) quello di andare a verificare il predimensionamento direttamente tramite la combinazione Slu + Neve. Estrapolando le tabelle excel in riferimento ad ogni gruppo di elementi strutturale (trave principale, trave secondaria, sbalzo e pilastro) si è notato che la sezione della trave principale risultava verificata al contrario della la sezione dello sbalzo e del pilastro che erano state sottodimensionati e della trave secondaria che era stata sovradimensionata.

Trave principale

Trave Secondaria

Sbalzo

Pilastro

Spinta del vento

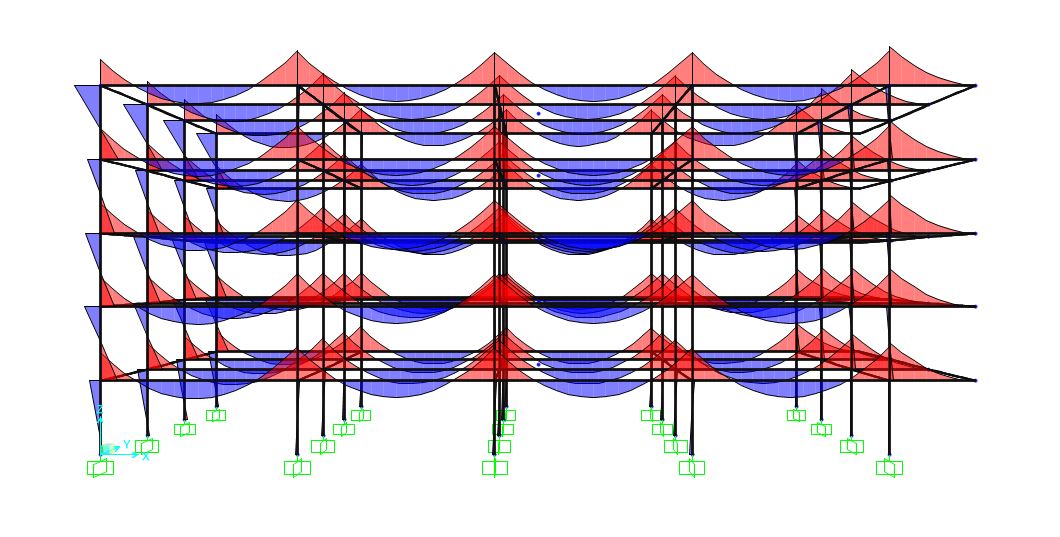
Definite le nuove sezioni si è passati ad analizzare la struttura sottoponendola alla spinta del vento. Si è scelto di studiare tale deformazione solo in direzione x poiché dalle precedenti analisi si è costatato che la deformata maggiore avveniva in tale direzione. Dalla nuova combinazione Slu+Vento si è notato che la sezione del pilastro non risultava ancora in grado di rispondere adeguatamente alla spinta del vento ed è stata di conseguenza maggiorata introducendo una nuova sezione.

Spinta sismica

Si è passati poi alla verifica della struttura sottoposta questa volta alla sollecitazione del sisma. Anche in questo caso la sollecitazione è stata posta in direzione x e. dopo aver calcolato le azioni sismiche su ogni piano della struttura ed estrapolati i dati riguardanti la pressoflessione agente sui pilastri, si è potuto costatare che la precedente sezione scelta non risultava adeguata anche per quanto riguarda le azioni sismiche ed è stata di conseguenza aumentata.

La prima parte dell'esercitazione consiste nel dimensionamento dei tre elementi strutturali principali di un telaio (trave, pilastro e sbalzo) in tre materiali differenti: legno, clacestruzzo armato e acciaio. 

Sono state progettati due tipi di strutture diverse, uno per il legno ed il calcestruzzo, l'altro per l'acciaio, entrambe destinate ad uno residenziale.

Quella per il legno/calcestruzzo presenta una luce per le travi principali di 4m, ed una luce per quelle secondarie di 5m; gli aggetti sono più contenuti, e si risolvono complessivamente in una luce di 2m. L'intero edificio si sviluppa su 4 piani, ma nei calcoli sono stati presi 5 per contare anche il solaio di copertura.

Quella per l'acciaio presenta una luce per le travi principali di 6m, ed una luce per quelle secondarie di 8m con gli sbalzi che arrivano a 3,50m. ANche in questo caso l'edificio si sviluppa su 4 piani, ma nei calcoli sono stati presi 5 per contare il solaio di copertura.

Durante il dimensionamento degli elementi, sono stati operate delle semplificazioni di calcolo e di schemi strutturali; infatti il dimensionamento non è avvenuto studiando lo schema strutturale di un trlaio, ma è avvenuto per i singoli elementi prendendo schemi statici semplificati: quello della trave doppiamente appoggiata per la trave, quello della mensola per lo sbalzo, e il pilastro come pilastrata soggetta a sforzo normale.

Sono state definite poi le tre tecnologie di solaio per la definizione dei calcoli strutturali, permanenti e variabili combinandoli alla SLU:

E' stato infine eseguito il dimensionamento di massima dei tre elementi, scegliendo quelli più sollecitati all'interno della struttura. Per ogni dimensionamento è stato usato un foglio di calcolo excel, e sono state eseguite le specifiche verifiche:

- TRAVE: nel clacestruzzo armato bisognava verificare che la sezione fosse idonea anche con l'aggiunta del peso             proprio dell'elemento

- SBALZO: in tutti e tre i materiali abbiamo dovuto verificare che la deformazione, e quindi l'abbassamento, non fosse eccessivo. Ricombinando i carichi alle SLE abbiamo perciò verificato che il rapporto tra luce/deformazione non fosse inferiore a 250. Per il calcestruzzo abbiamo nuovamente dovuto verificare che la sezione fosse idonea anche con l'aggiunta del peso proprio dell'elemento.

- PILASTRO: per tutti e tre i materiali abbiamo dovuto verificare la sezione all'instabilità euleriana, verificando di non progettare elementi troppo snelli e che quindi rispondessere in maniera corretta al carico critico. Per il calcestruzzo si è inoltre dovuta operare una verifica a pressoflessione, verificando la sezione anche a questo sforzo.

Dai calcoli svolti si è arrivati a queste sezioni:

LEGNO

- TRAVE di 30cm x 40cm

- MENSOLA 30cm x 35cm

- PILASTRO 30cm x 25cm

CALCESTRUZZO ARMATO:

- TRAVE di 30cm x 55cm

- MENSOLA 30cm x 45cm

- PILASTRO 30cm x 35cm

ACCIAIO:

- TRAVE IPE500

- MENSOLA IPE450

- PILASTRO HEA280

In allegato il file con tutta l'esercitazione in dettaglio.

Si è scelto di progettare una travatura reticolare di modulo 2,5m x 2,5m x 2,5m che rifondasse un edificio di 5 piani. collocata al primo, si compone di 10 moduli orizzontali e 7 verticali per una dimensione complessiva di 25 m x 17,5m x 2,5m. I incoli sono stati disposti ai 4 angoli, con un piccolo aggetto perimetrale pari ad un moudlo. La struttura ha l'obbietti di sostenere quindi un carico compelssivo di 21.926,42kN. 

Tramite SAP 2000 ho disegnato l'elemento strutturale partendo dal modulo realizzato in AutoCAD dandogli successivamente un primo predimensionamento. Ciò mi ha permesso di analizzare in un primo momento la sollecitazione dovuta dal solo carico strutturale e le relative deformaizoni, e poi anche quelle dovute dai carichi del resto dell'edificio ( i 5 piani superiori ).

Si sono successivamente evidenziati i diagrammi delle sollecitazioni e riportate le tabelle con i valori dello sforzo normale di ogni asta su Excel. Da qui sono riuscita a suddividere i profili in classi da 80 - 90 elementi, ed assegnare ad ogni classe una sezione dimensionata sull'elemento più sollecitato. Si sono individuate quindi 4 classi per gli elementi tesi e 4 per quelli compressi, ogninua con una propria sezione individuata dai profilari presi come riferimento.

Dopo questa prima analisi sono state fatte varie osservazioni e riflessioni sui risultati ottenuti, andando a modificare quelle che sarebbero potute essere sezioni "migliorabili" e in che modo si è cercata questa ottimizzazione. 

In allegato il file dell'esercitazione, e i relativi fogli excel con i calcoli