blog di Stefano.Botta

L'esercitazione consiste nell’inserimento in SAP2000 della struttura precedentemente dimensionata, nonché della conseguente verifica delle sezioni mediante i dati forniti dal software. Anche in questo caso sono state prese in considerazione due tipi di strutture diverse realizzate in tre materiali diversi: legno, calcestruzzo e acciaio.

TELAIO IN CALCESTRUZZO ARMATO

Si è iniziato disegnando lo schema strutturale in SAP2000 di tutti gli elementi del piano terra che poi sono stati duplicati in altezza; ogni elemento è stato disegnato come un frame separato in modo da andare a generare dei nodi rigidi, vincolando alla fine i pilastri del piano terra con degli incastri al suolo. Si è quindi passati alla definizione del materiale e delle sezioni come definite dall’esercitazione.

A questo punto si è passati all’inserimento dei carichi distribuiti lungo le travi principali. Nel calcolo strutturale questi sono stati combinati tra loro attraverso la SLU alla quale poi sono state aggiunte in seguito anche le forze orizzontali dovute dal vento e dal sisma.

Sono state estrapolate le tabelle delle sollecitazioni di ogni singolo gruppo di elementi. Dalla tabella excel si cerca il valore massimo del momento sia per le travi primarie che per le secondarie e gli sbalzi. Per le travi il momento massimo trovato risulta essere comunque più basso rispetto a quello calcolato in precedenza, questo perché nel nodo rigido il momento è passate, e quindi diverso da zero, permettendo di avere una sollecitazione in mezzeria sensibilmente minore. Provando a eseguire il dimensionamento con il nuovo valore del momento, si è potuto constatare che la sezione scelta precedentemente era adeguata e per questo è stata mantenuta.

Lo stesso procedimento è stato svolto per il calcolo della trave secondaria, in questo caso il momento risultava essere molto più basso rispetto a quello della primaria. La si è comunque dimensionata leggermente più grande rispetto ai valore calcolato.

Per quanto riguarda lo sbalzo, anche in questo caso si è svolta nuovamente l’operazione di ridimensionamento e verifica all’abbassamento come svolto nella parte dell’esercitazione precedente; l'elemento è stato ottimizzato poiché era risultato sovradimensionato nella prima parte dell'esercitazione.

Per quanto riguarda il pilastro si è proceduto attraverso il dimensionamento e la verifica a snellezza della sezione prendendo in considerazione lo sforzo assiale agente mediante i calcoli svolti in precedenza. I pilastri sono stati poi verificati a pressoflessione in un secondo momento.

Carico neve

Una volta definite le sezioni di tutti e quattro gli elementi, si è continuato attraverso la verifica degli elementi nel caso in cui questi siano sottoposti ad un carico maggiorato dal peso della neve. La maggiorazione dipende da moltissimi fattori quali la zona climatica in cui si trova l’edificio sottoposto al calcolo, la tipologia del tetto, la sua inclinazione, la possibilità di essere o meno riscaldato e altri. Nel mostro caso abbiamo ipotizzato un peso di circa 0,5 kN/m²  e abbiamo quindi operato un calcolo alla SLU + neve, verificando che gli sforzi negli elementi maggiormente sollecitati non aumentano in modo eccessivo, e che quindi le sezioni calcolate alla SLU erano verificate anche per il carico neve.

Spinta del vento

A questo punto si è passati alla verifica degli elementi verticali alle spinte orizzontali. Sia per il vento che per il sisma non siamo in grado di sapere quale sia la direzione precisa con cui investiranno la struttura, per questo motivo andremo a svolgerci un’analisi sia per la direzione in x, sia per la direzione in y, verificheremo per quale delle due i nostri elementi saranno più sollecitati e svolgeremo il dimensionamento.

Il vento è considerato un agente dinamico, e quindi che varia di intensità e direzione nel tempo. Per questo motivo si è scelto di semplificare il caso preso in esame ipotizzando il vento come un agente statico, che imprimesse un carico distribuito differente sui pilastri posti in pressione e depressione. Dall’analisi allegata di seguito, si è deciso di prendere in considerazione solo il momento sui pilastri nella direzione x, in quanto risulta essere quella che maggiormente stressa il pilastro a flessione e compressione.

Spinta sismica

La forza sismica che investe un edificio è caratterizzata da due grandezze principali: l’accelerazione, calcolata dall’energia che ci si aspetta venga sprigionata durante il sisma e che dipende dalla zona dove ci si trova espressa in una frazione di g, e la massa, e quindi il peso, dell’edificio. Sapendo che la forza sismica non si distribuisce verticalmente in maniera costante lungo tutto l'edificio (e quindi aumenta con il salire degli impalcati), ci si è calcolati la forza concentrata nel centro d’area di ogni impalcato come semplificazione dell'azione sismica. Anche in questo caso si è svolta prima la verifica lungo la direzione x, e poi lungo quella y, andando poi a constatare che anche in questo caso gli elementi risultavano più sollecitati se investiti da una forza proveniente dalla direzione x. 

TELAIO IN LEGNO

Per quanto riguarda il dimensionamento e la verifica del telaio in Legno su SAP2000, è stata impiegata la medesima struttura elaborata per il calcestruzzo armato (dato che queste due erano geometricamente identiche), agendo su materiali e sezioni degli elementi. I carichi definiti per i solai e la destinazione d’uso nella prima parte dell’esercitazione sono stati ripartiti sulle travi principali, facendo riferimento alla fascia di spettanza di queste. È stato quindi definito un nuovo materiale legno lamellare riportando i parametri impiegati precedentemente sul programma.

Il passo successivo è stato quello di andare a verificare il pre-dimensionamento degli elementi riportati sul programma rispetto allo SLU, questa volta facendo anche riferimento al carico distribuito della neve. Dall’analisi è conseguito che la prima ingegnerizzazione  delle travi principali  risultava essere leggermente sovradimensionata; la sezione è stata leggermente ridotta rispetto alla nuova analisi. La trave secondaria è stata dimensionata secondo lo stesso iter della principale, rispetto al momento flettente massimo estrapolato da SAP2000, ma l’altezza minima era così piccola che si è deciso di portare la sezione a un’altezza uguale a quella della principale. Per ciò che riguarda lo sbalzo, per quanto il momento flettente ricavato dall’analisi su SAP2000 fosse leggermente più alto, la differenza era così piccola che la sezione è rimasta la stessa rispetto a quella pre-dimensionata. Anche nel caso del pilastro ci si è trovati nella situazione di non dover alterare il pre-dimensionamento in quanto lo sforzo assiale ottenuto dall’analisi mediante il programma non influiva in modo marcato sul nuovo progetto della sezione.

Spinta del vento

Una volta assegnate le nuove sezioni ingegnerizzate sul telaio elaborato in SAP2000 si è passati ad effettuare una verifica della struttura rispetto all’azione del vento. In particolare, avendo notato già rispetto al caso del calcestruzzo armato che la direzione più sollecitata era quella X (la direzione parallela al lato lungo dell’edificio)  si è deciso di eseguire solamente tale verifica. Dall’analisi rispetto a questo carico orizzontale è stata estrapolata una tabella relativa alle sollecitazioni assiali e ai momenti agenti su tutti i pilastri; su di essa è stata fatta una verifica a pressoflessione progettando un foglio excel per calcolare le tensioni assiali e flessionali di ogni pilastro e controllare che la somma dei rapporti fra queste e le relative resistenze di progetto (parallele alla fibra e a flessione) fossero minori o uguali a 1. L’esito della verifica è stato positivo, quindi non è stato necessario tornare sul dimensionamento degli elementi.

Spinta sismica

Si è effettuato infine un’analisi sul telaio rispetto all’azione sismica (sempre in direzione X, la direzione più sollecitata come riscontrato in precedenza), andando a calcolare per ogni impalcato quale fosse la forza sismica agente e attribuendo quest’ultima come carico concentrato nel centro d’area di ogni singolo piano. La verifica è risultata anche in questo caso positiva, per cui le sezioni ingegnerizzate sono state mantenute come tali.

TELAIO IN ACCIAIO

Per il dimensionamento e la verifica del telaio in Acciaio si è iniziato modificando la struttura precedentemente utilizzata, per l’analisi dei telai in legno e calcestruzzo, al fine di renderla coerente con l’ipotesi di progetto effettuata nella prima parte dell’esercitazione. Oltre a modificare le dimensioni della struttura sono stati modificati anche i carichi su di essa agenti.

Il passo successivo è stato (come nel caso del telaio in legno) quello di andare a verificare il predimensionamento direttamente tramite la combinazione Slu + Neve. Estrapolando le tabelle excel in riferimento ad ogni gruppo di elementi strutturale (trave principale, trave secondaria, sbalzo e pilastro) si è notato che la sezione della trave principale risultava verificata al contrario della la sezione dello sbalzo e del pilastro che erano state sottodimensionati e della trave secondaria che era stata sovradimensionata.

Spinta del vento

Definite le nuove sezioni si è passati ad analizzare la struttura sottoponendola alla spinta del vento. Si è scelto di studiare tale deformazione solo in direzione x poiché dalle precedenti analisi si è costatato che la deformata maggiore avveniva in tale direzione. Dalla nuova combinazione Slu+Vento si è notato che la sezione del pilastro non risultava ancora in grado di rispondere adeguatamente alla spinta del vento ed è stata di conseguenza maggiorata introducendo una nuova sezione.

Spinta sismica

Si è passati poi alla verifica della struttura sottoposta questa volta alla sollecitazione del sisma. Anche in questo caso la sollecitazione è stata posta in direzione x e, dopo aver calcolato le azioni sismiche su ogni piano della struttura (attraverso l’utilizzo della formula di Navier) ed estrapolati i dati riguardanti la pressoflessione agente sui pilastri, si è potuto costatare che la precedente sezione scelta risultava adeguata anche per quanto riguarda le azioni sismiche.

L'Esercitazione 2 consisteva nel dimensionamento di tre strutture intelaiate realizzate in materiali differenti e con tecnologie di solaio diverse. Nel progettare tali strutture, si è deciso di ipotizzare lo stesso modello di edificio per quanto riguardava il calcestruzzo armato e il legno, definendone poi un altro con luci più ampie per l'acciaio. 

Trattandosi di un pre-dimensionamento degli elementi più sollecitati (travi, sbalzi e pilastri), si sono adottati dei modelli semplificati per l'analisi delle sollecitazioni agenti su questi così da permetterne la progettazione. Le travi sono state trattate come doppiamente appoggiate, gli sbalzi come mensole e i pilastri sono stati considerati come singole pilastrate contenenti gli elementi dal pian terreno all'ultimo livello.

Schema Trave Doppiamente Appoggiata:

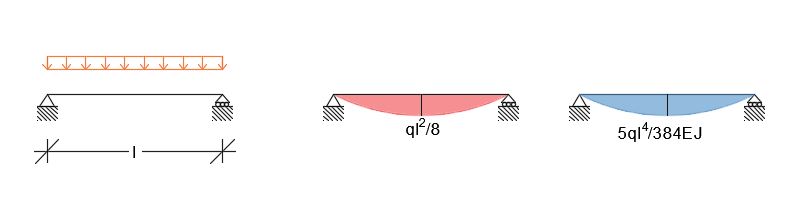
Schema Mensola:

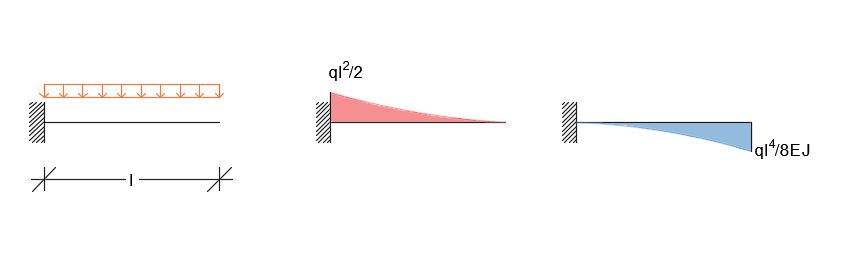
Schema Pilastrata:

TELAIO IN CALCESTRUZZO ARMATO

La struttura ipotizzata per il calcestruzzo armato (come per il legno) si presenta come un telaio formato da moduli rettangolari 5,00 m x 4,00 m, per un totale di cinque piani di altezza 3,00 m ciascuno; sul versante destro reca uno sbalzo di due metri che ricorre per ogni piano.

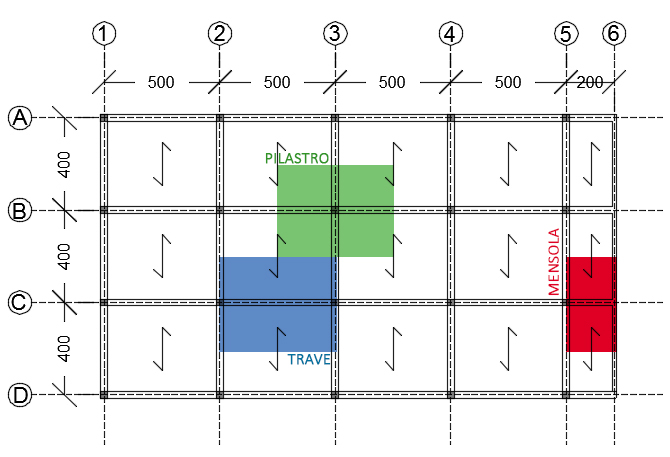
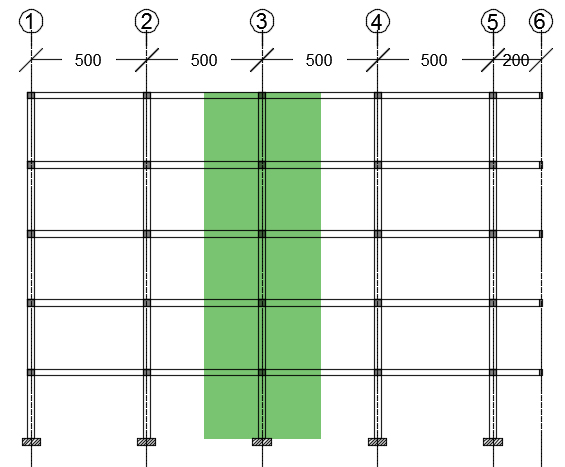
Stratigrafia del Solaio in Calcestruzzo Armato:
1 - Intonaco civile: 2,00 cm
2 - Travetti prefabbricati: 10,00 x 20,00 cm
3 - Pignatta in laterizio: 40,00 x 20,00 cm
4 - Caldana: 5,00 cm
5 - Isolante (lana di legno): 4,00 cm
6 - Massetto: 3,00 cm
7 - Parquet (legno di ciliegio): 2,00 cm

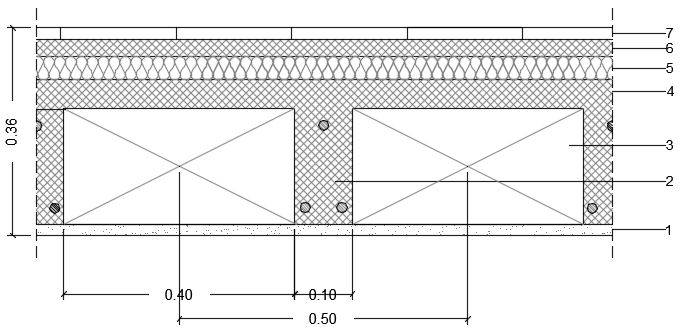
Il primo passo è stato quello di analizzare e calcolare quali fossero i carichi agenti su tale solaio. Il carico strutturale stimato è 4,17 kN/m², i sovraccarichi permanenti sono 1,29 kN/m², mentre i carichi accidentali (derivanti dalla destinazione d'uso, in questo caso un'abitazione) sono 2,00 kN/m² secondo la Normativa.

Trave in calcestruzzo armato:
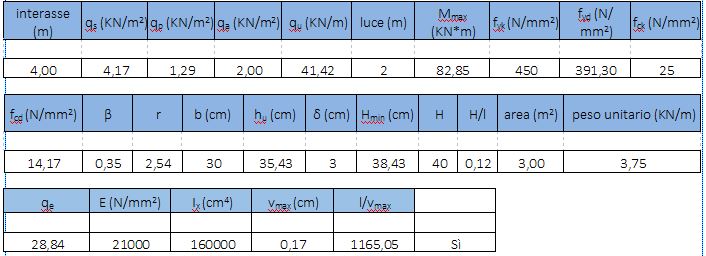
Una volta determinato la trave più sollecitata, è stato calcolato il carico allo Stato Limite Ultimo, così da ottenere poi il carico distribuito su tale elemento (prendendo in considerazione la sua fascia di influenza).
Una volta conosciuto il momento massimo rispetto al modello di trave appoggiata appoggiata, avendo scelto i materiali della sezione (e quindi le rispettive resistenze caratteristiche di calcestruzzo e acciaio, trasformate poi in valori di progetto), è stata calcolata l'altezza utile della trave (ipotizzandone la base); tale dimensionamento fa riferimento ad una grandezza r che dipende sia dalla resistenza del calcestruzzo, sia dal rapporto che intercorre tra di essa e la sua somma con quella dell'acciaio omogeneizzato. La tave è stata a questo punto ingegnerizzata e si è effettuata una verifica della sezione progettata rispetto al peso proprio, aggiungendo quest'ultimo ai carichi strutturali per constatare se anche in queste condizioni l'altezza utile fosse ancora al di sotto di quella ingegnerizzata.

Sbalzo in Calcestruzzo armato:
Considerando lo stesso carico allo S.L.U. della trave, è stato calcolato il momento massimo dello sbalzo (facendo riferimento al modello semplificato di mensola). Analogamente alla trave, e impiegando gli stessi materiali (le medesime classi di resistenza), è stata ricavata l'altezza utile della sezione. La sezione è stata quindi ingegnerizzata ed è stata anche qui fatta una verifica rispetto al peso proprio dell'elemento.
Si è verificato a questo punto l' abbassamento dell'elemento, del quale conoscevamo sia il modulo elastico che il momento di inerzia. Una volta calcolato il carico rispetto allo Stato Limite di Esercizio, si è determinato l'abbassamento massimo si è verificato che il rapporto tra la luce delle elemento e quest'ultimo fosse maggiore o uguale al valore imposto dalla Normativa.

Pilastro in Calcestruzzo armato:
Una volta individuato il pilastro più sollecitato nel telaio, è stato calcolato lo sforzo normale massimo (rispetto al modello della pilastrata) considerando non solo il carico del solaio ma anche quello delle travi comprese nell'area di influenza dell'elemento (il tutto moltiplicato per il numero di piani della struttura). Mediante lo sforzo normale massimo è stato possibile effettuare il dimensionamento della sezione; in questo caso, per far fronte al problema dell'instabilità, è stata presa in considerazione la snellezza dell'elemento per determinare le dimensioni geometriche che ne garantissero una giusta risposta: tramite il raggio minimo di inerzia si è potuto definire la base minima, e successivamente l'altezza minima. Il pilastro è stato ingegnerizzato ed è stata fatta una verifica rispetto alla presso-flessione per controllare che la tensione massima fosse minore della resistenza di progetto.

TELAIO IN LEGNO

Per il dimensionamento degli elementi del telaio in legno si è presa come struttura di riferimento la stessa ipotizzata per il calcestruzzo armato.

Stratigrafia delSolaio in Legno:
1 - Travetti in legno: 100 x 80 mm
2 - Tavolato in legno: 250 mm
3 - Caldana: 40 mm
4 - Isolante (lana di legno): 40 mm
5 - Massetto: 30 mm
6 - Parquet (legno di ciliegio): 20 mm

Il carico strutturale stimato in questo caso è 1,21 kN/m², i sovraccarichi permanenti sono 0,89 kN/m², mentre i carichi accidentali sono 2,00 kN/m² poiché la destinazione d'uso è la medesima.

Trave in Legno: 
Nel dimensionamento di una trave in legno il procedimento iniziale di analisi dei carichi e determinazione del momento massimo avviene in modo analogo al calcestruzzo. Si è considerata poi la resistenza a flessione caratteristica del legno lamellare per determinarne il valore di design (che in questo caso fa riferimento anche alla classe di durata di carico della struttura, che si suppone permanente). Una volta ipotizzata la base della trave, è stata calcolata l'altezza minima di questa, la quale è stata ingegnerizzata. Non è stata effettuata la verifica rispetto al peso proprio in questo caso (come anche per l'acciaio) poiché gli elementi progettati in questi materiali sono solitamente più leggeri e influenzano poco il carico strutturale.

Sbalzo in Legno:
Procedendo in modo analogo a quanto fatto per il calcestruzzo armato, è stata effettuata un'analisi del carico allo S.L.U. ed è stato calcolato il momento massimo agente sull'elemento al fine di progettarne l'altezza minima (dando sempre la base come ipotesi), così da effettuare successivamente l'ingegnerizzazione della sezione.
Anche in questo caso, come per la trave, non è stata fatta una verifica rispetto al peso proprio. Si è infine proceduto alla verifica dell'abbassamento massimo dello sbalzo come si è fatto per il calcestruzzo.

Pilastro in Legno:
Analizzando i carichi e facendo riferimento allo sforzo normale ottenuto, è stata calcolata l'area minima della sezione del pilastro. Anche in questo caso, per tenere conto del fenomeno dell'instabilità, ci si è riferiti alla snellezza dell'elemento e al suo raggio di inerzia; trattandosi di un materiale anisotropo, il modulo elastico considerato in questo caso è quello parallelo alle fibre e quindi risulta ridotto rispetto a quello impiegato nella trave. In questo modo è stata calcolata la base minima e di conseguenza l’altezza minima della sezione come rapporto fra l'area minima e la base ingegnerizzata.

TELAIO IN ACCIAIO

La struttura intelaiata ipotizzata per l'acciaio è composta da moduli 8,00 m x 4,00 m e reca uno sbalzo sul versante destro di 3,50 m, per un totale di 5 piani anche in questo caso.

Stratigrafia del Solaio in Acciaio:

Il carico strutturale qui stimato è 2,10 kN/m², i sovraccarichi permanenti sono anche in questo caso 0,89 kN/m², mentre i carichi accidentali restano 2,00 kN/m² per la stessa destinazione d'uso.

Trave in Acciaio:
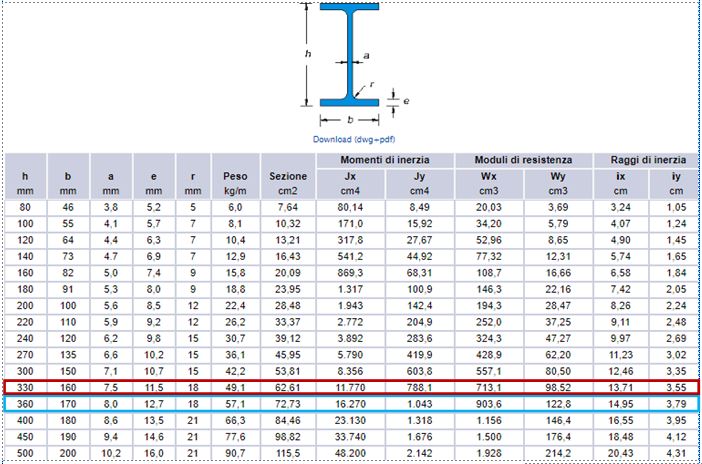
Pur cambiando la tecnologia del solaio e di conseguenza i carichi, il procedimento di determinazione del carico allo S.L.U. e di calcolo del momento massimo è analogo a quelli precedentemente applicati. Una volta scelto il tipo di acciaio (perciò la sua classe di resistenza) e definita la resistenza di progetto f_yd, è stato cacolato il modulo di resistenza a flessione minimo. La sezione è stata a questo punto ingegnerizzata facendo riferimento a un sagomario di profili IPE (da immagine, in azzurro) scegliendone uno con W_x maggiore rispetto a quello minimo determinato.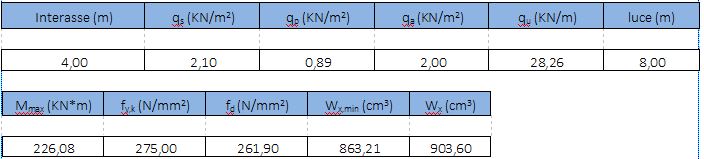

Sbalzo in Acciaio:
Per dimensionare lo sbalzo si è proceduto anche in questo caso all'analisi dei carichi e al calcolo del momento massimo così da poter determinare il modulo di resistenza a flessione minimo W_x e passare quindi all'ingegnerizzazione della sezione (tramite lo stesso sagomario di IPE utilizzato per la trave, nell'immagine in rosso). Non è stata effettuata nessuna verifica rispetto al peso proprio dell'elemento, in quanto anche in questo caso (come per il legno) è da considerarsi poco influente. È stato verificato infine che il rapporto fra la luce e l'abbassamento massimo della trave superasse il valore definito dalla Normativa.

Pilastro in Acciaio:
Per il dimensionamento del pilastro in acciaio si è proceduto come nel caso degli altri pilastri per ricavare lo sforzo assiale massimo; è stata scelta la medesima classe di resistenza dei materiali di trave e sbalzo ed è stata calcolata l'area minima della sezione. Si è anche qui tenuto conto del fenomeno del carico critico euleriano considerando la snellezza e attraverso questa sono stati calcolati il raggio di inerzia minimo e al momento di inerzia minimo, mediante i quali si è passati all'ingegnerizzazione della sezione, riferendosi a un sagomario di profili HEA e scegliendo una sezione avente valori maggiori di quelli determinati.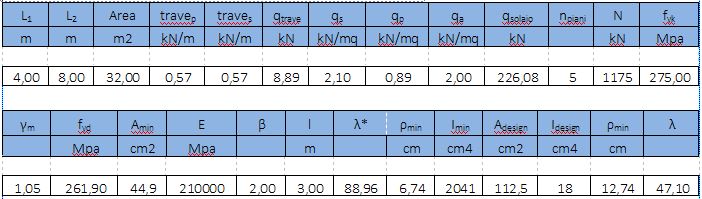

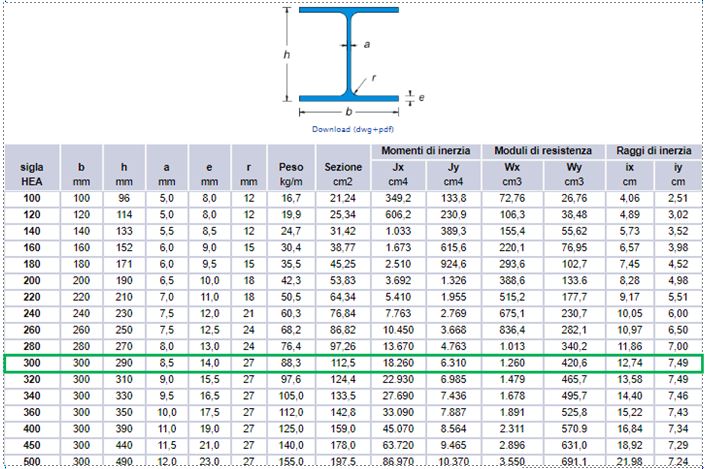
ALLEGO alla pagina un documento pdf esplicativo di tutti i passaggi effettuati nel dettaglio e dei relativi calcoli di dimensionamento.

Progetto di una trave reticolare spaziale in acciaio atta a coprire un'aula quadrata di lato 27,00 m e sostenere quattro piani sovrastanti

In questa prima esercitazione (allegata al post) abbiamo dimensionato una trave reticolare tridimensionale effettuando dapprima un'ipotesi progettuale, per poi andare a ridisegnare la struttura ipotizzata mediante il programma SAP2000 così da poter effettuare delle analisi su di essa, traendo informazioni relative agli sforzi assiali agenti sulle singole aste e al mondo in cui questa si deforma.

Mediante i dati ricavati dalla progettazione virtuale della reticolare abbiamo potuto effettuare dei calcoli per il dimensionamento degli elementi, suddividendoli in tesi e compressi e distribuendoli in più classi (4 a trazione e 4 a compressione) così da avere in totale 8 aste di cui determinare il profilo (la maggiore per ogni classe in termini di sforzo assiale), così da ottimizzare le sezioni e ridurre l'impiego di acciaio (abbiamo fatto riferimento al profilario di Fondazione Promozione Acciaio).

Una volta effettuato il dimensionamento attraverso un foglio excel, abbiamo provato a formulare delle ipotesi per cambiare la reticolare in modo tale da ridurre i valori degli sforzi assiali sulle aste (e di conseguenza anche i profili a esse attribuibili), e capire come/quanto le sollecitazioni possano cambiare al variare delle scelte strutturali sul medesimo progetto. 

Dati relativi alla struttura e ai carichi sovrastanti la reticolare:

Immagini della trave reticolare spaziale progettata su SAP2000, alla relativa consigurazione deformata e ai diagrammi degli sforzi assiali sulle aste della struttura:

Tabelle relative ai dimensionamenti delle aste in trazione:

Tabelle relative ai dimensionamenti delle aste in compressione: