blog di francesca.secci

TRAVE VIERENDEEL

In questo esercizio risolveremo una trave Vierendeel 

cos’è una TRAVE VIERENDEL? È una travatura reticolare costituita da due correnti collegati tra loro da montanti che però non presenta elementi diagonali. A differenza della travatura reticolare che lavora solo per sforzo normale sia nei montanti  che nei correnti c’è taglio e momento flettente. Per funzionare bene  gli elementi verticali devono essere molto rigidi a flessione.

Ipotizziamo che i montanti risultino rigidi, dunque Il telaio può essere associato ad un TELAIO Shear Type capovolto, ossia un telaio con tutti i nodi ad incastro e in cui si ipotizza la rigidezza flessionale infinita della trave rispetto ai pilastri.

Analizziamo un Telaio shear type:

Nei ritti ho una situazione a doppio incastro e con l’integrazione della linea elastica mi trovo i valori di taglio e momento. Dove i ritti si innestano nel traverso lo stato tensionale (taglio,momento) agirà nel traverso uguale ed opposto

Ora passiamo alla trave VIERENDEEL a mensola

I montanti  si trovano in una situazione di doppio incastro che risolvo con l’integrazione della linea elastica mi trovo i valori di taglio e momento (come svolto prima nel telaio shear-type)

Mi pongo l’equilibrio alla traslazione verticale così da trovarmi lo spostamento,il taglio e il momento

Mi posso disegnare I diagrammi di taglio e momento

Sapendo il momento dei traversi mi mi trovo il momento dei montanti verticali imponendo l’equilibrio ai nodi

Per trovarmi il taglio impongo l’equilibrio dei i traversi verticali, il taglio si trova facendo la somma dei momenti dividendola per la luce dell’asta

Ora mi posso diosegnare i diagrammi del taglio e del momento dei montanti verticali

Risoluzione di una struttura iperstatica attraverso il METODO DELLE FORZE

Ho una struttura 3 volte iperstatica

La risolvo con il metodo delle forze

1)Definisco la STRUTTURA ISOSTATICA DI RIFERIMENTO

2)EQUAZIONI di COMPATIBILITÁ CINEMATICA

Δϕ(B)=0 

ma dato che la struttura è simmetrica sappiamo che  Δϕ(B)= Δϕ(D)=0

PUNTO B

ϕ(Bs)=ql³/24EI-X₁l/3EI

ϕ(Bd)=-ql³/24EI+X₁l/3EI +X₂l/6EI

PUNTO C

ϕ(Cs)=ql³/24EI-X₂l/3EI- X₁l/6EI

ϕ(Cd)=-ql³/24EI+X₂l/3EI +X₁l/6EI

ϕ(Bs)= ϕ(Bd)    ql³/24EI-X₁l/3EI=-ql³/24EI+X₁l/3EI +X₂l/6EI

X₁=ql²/8- X₂/4

ϕ(Cs)= ϕ(Cd)     ql³/24EI-X₂l/3EI- X₁l/6EI=-ql³/24EI+X₂l/3EI +X₁l/6EI

X₂= ql²/8- X₁/2

Andando poi a sostituire X₁=ql²/8- X₂/4 in X₂= ql²/8- X₁/2       X₁=3ql²/28

E poi   X₁=3ql²/28 in  X₂= ql²/8- X₁/2 ottengo                              X₂=ql²/14

3)CALCOLO DELLE REAZIONI VINCOLARI

Trovate le incognite iperstatiche procedo con il calcolo delle reazioni vincolari applicando il principio di sovrapposizione degli effetti.

STRUTTURA CONSIDERANDO IL CARICO q

STRUTTURA CONSIDERANDO X₁,X₂

4)SOMMO LE REAZIONI VINCOLARI

5)DISEGNO i diagrammi del TAGLIO e del MOMENTO

DIMENSIONAMENTO DI UNA TRAVE in CEMENTO ARMATO

 Disegno un telaio strutturale, avente :

Interasse (I)= 5m

Luce(L)=6m

Vado ad analizzare la trave più sollecitata

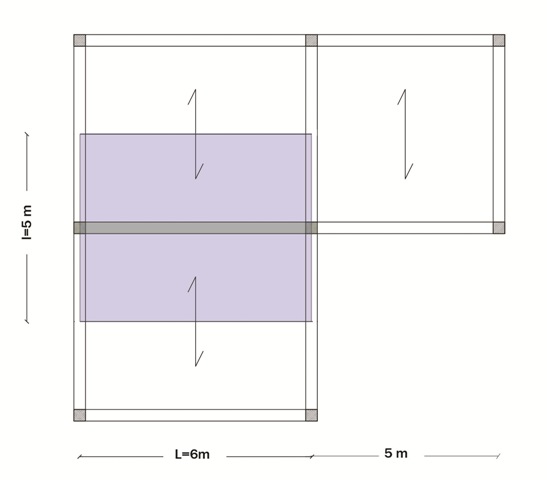
Ho deciso di adottare una solaio misto  in latero cemento ipotizzando un’altezza H>L/25  perciò H>0.24m

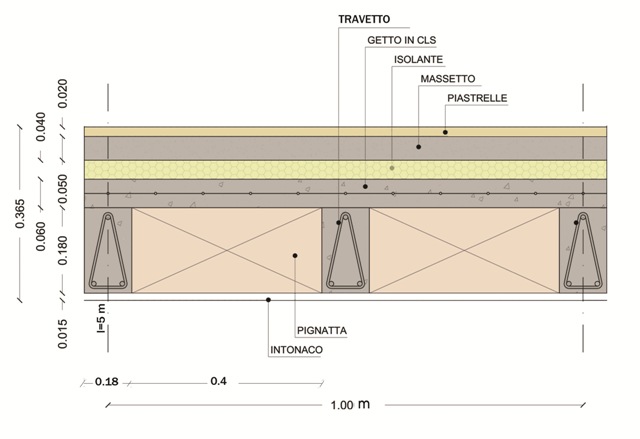
ANALISI DEI CARICHI

1)CARICHI STRUTTURALI  Qs

peso di tutti gli elementi   strutturali=TRAVETTO-PIGNATTA-SOLETTA

Per trovare il qs al mq di ogni elemento faccio:

larghezza x altezza x profondità x peso specifico materiale

 -TRAVETTI  :

peso specifico del cemento =25 KN/ m³  

0,1 x 0,18 x 1 x 25 = 0,45 x 2 = 0,9 KN/ m²  

-PIGNATTE :

peso specifico mattoni forati =8    KN/m³

0,40 x 0,18 x 1 x 8 KN/m³  = 0,576 KN/m²x 2 = 1,152 KN/m²       

-SOLETTA:

Peso specifico delcemento 25 KN/ m³

1 X 1 X 0,06 X 25 =  1,5  KN/ m²          

 qs TOT = 1,152+0,9+1,5 = 3,552 KN/ m²

 2)CARICHI  PERMANENTI Qp

peso dei carichi permanenti dei restanti  elementi (dunque non strutturali) che compongono il pacchetto solaio =Massetto—isolante-piastrelle

 -MASSETTO

peso specifico materiale calcestruzzo sabbia 18 KN/ m³

0,05 x 1 x 1 x 18 = 0,9 KN/ m²  

-ISOLANTE

peso specifico fibre minerali 0,5 KN/ m³

1 x 1 x 0,04 x 0,5 = 0,02 KN/ m²       

-PIASTRELLE

Peso specifico gres porcellanato 23 KN/ m³

1 x 1 x 0,02 x 23 = 0,46 KN/ m²            

-INTONACO SOFFITTO

peso specifico materiale (malta di calce 18 KN/ m³)

0,015 x 1 x 1 x 18 = 0,27 KN/ m²              

-INCIDENZA IMPIANTI  :  0,5 KN/ m²               

-INCIDENZA TRAMEZZI  : 1,60 KN/ m²

 qp TOT =  0,27+0,02+0,9+0,46 = 3,75 KN/ m²

 3)CARICHI ACCIDENTALI Qa

Dipende dalla funzione dell’edificio in quanto si considera la variazione dei carichi che può gravare o meno sul solaio

Ipotizzando che la destinazione d’uso di questo edificio sia un ambiente a uso residenziale,normativa prevede  Qa  =2 KN/m²

sommatoria dei carichi:

Q TOT = Qs +Qp + Qa = 3,552 + 3,75 + 2 = 9,30 KN/ m²

INSERISCO I VALORI TROVATI SULLA TABELLA EXEL

Interasse=3,5525 KN/ m²  

Qp=3,75 KN/ m²  

QS=2 KN/ m²  

moltiplicando la somma dei carichi per l’interasse I ottengo il q =  46,51kN/m

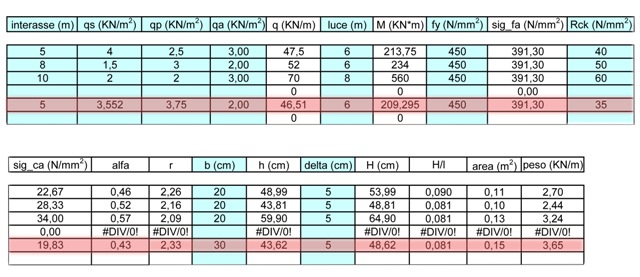
Essendo la trave doppiamente appogiatae avente una Luce =6m, ottengo il Momento flettente massimo (qL ²/ 8) = 209,295 KN*   m

Definisco la  classe di resistenza dell’acciaio da  armatura B450C deve essere 450MPa.

Inserisco fy (Limite di snervamento)Dividendo fy per un coefficiente di sicurezza pari a 1,15 ottengo così anche sig_fa ( la resistenza di calcolo dell’acciaio che è riferita alla tensione di snervamento)

Definito un Rck (la resistenza caratteristica cilindrica a compressione del calcestruzzo a 28 giorni) uguale a 35 sig_ca = Rck  x 0,85 (il coeffciente riduttivo per le resistenze di lunga durata)/1,5 (il coefficiente parziale di sicurezza relativo al calcestruzzo)

Ottengo così l’altezza della traveH =48, 62 cm