- Correzione tavola 6 2 anni 8 mesi fa
- diagrammi graticcio 6 anni 5 mesi fa
- ultima domanda 6 anni 5 mesi fa
- no ho ancora un'ultima 6 anni 5 mesi fa
- sì sì tutto chiaro. 6 anni 5 mesi fa
- Load Pattern peso proprio 6 anni 5 mesi fa
- Ciao Fabiana, 6 anni 5 mesi fa
- Ciao Giuliana, 6 anni 5 mesi fa
- Modellazione setto - Giuliana Nardi 6 anni 5 mesi fa
- assegnare sezione a setti su sap 6 anni 5 mesi fa
esercitazione struttura iperstatica
Risoluzione di una struttura iperstatica attraverso il METODO DELLE FORZE
Ho una struttura 3 volte iperstatica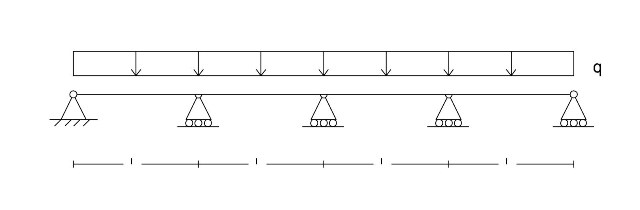
La risolvo con il metodo delle forze
1)Definisco la STRUTTURA ISOSTATICA DI RIFERIMENTO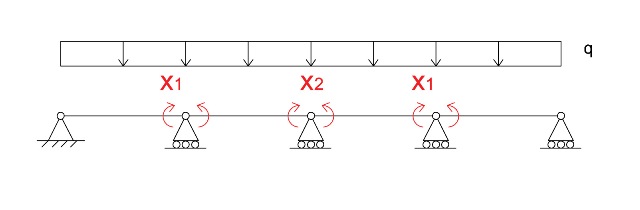
2)EQUAZIONI di COMPATIBILITÁ CINEMATICA
Δϕ(B)=0
ma dato che la struttura è simmetrica sappiamo che Δϕ(B)= Δϕ(D)=0
PUNTO B
ϕ(Bs)=ql³/24EI-X₁l/3EI
ϕ(Bd)=-ql³/24EI+X₁l/3EI +X₂l/6EI
PUNTO C
ϕ(Cs)=ql³/24EI-X₂l/3EI- X₁l/6EI
ϕ(Cd)=-ql³/24EI+X₂l/3EI +X₁l/6EI
ϕ(Bs)= ϕ(Bd) ql³/24EI-X₁l/3EI=-ql³/24EI+X₁l/3EI +X₂l/6EI
X₁=ql²/8- X₂/4
ϕ(Cs)= ϕ(Cd) ql³/24EI-X₂l/3EI- X₁l/6EI=-ql³/24EI+X₂l/3EI +X₁l/6EI
X₂= ql²/8- X₁/2
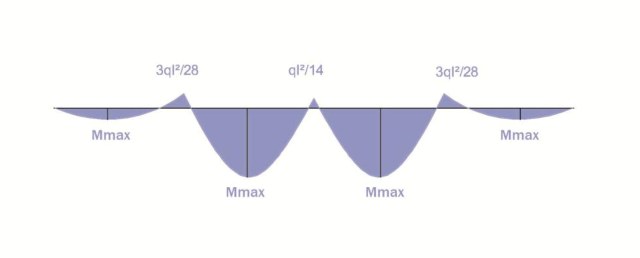
Andando poi a sostituire X₁=ql²/8- X₂/4 in X₂= ql²/8- X₁/2 X₁=3ql²/28
E poi X₁=3ql²/28 in X₂= ql²/8- X₁/2 ottengo X₂=ql²/14
3)CALCOLO DELLE REAZIONI VINCOLARI
Trovate le incognite iperstatiche procedo con il calcolo delle reazioni vincolari applicando il principio di sovrapposizione degli effetti.
STRUTTURA CONSIDERANDO IL CARICO q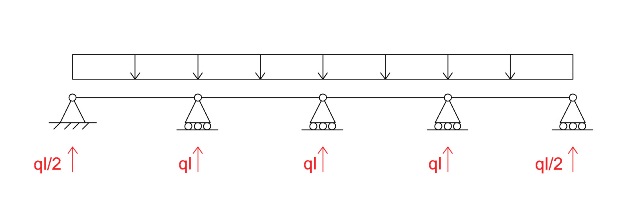
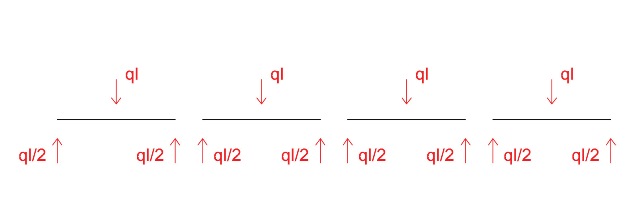
STRUTTURA CONSIDERANDO X₁,X₂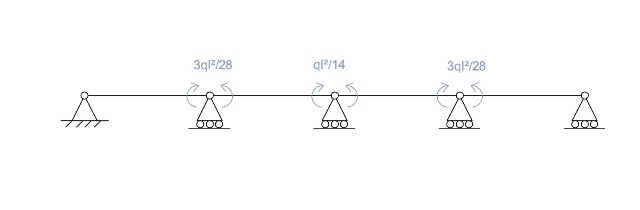
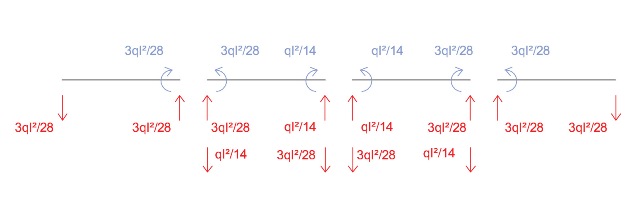
4)SOMMO LE REAZIONI VINCOLARI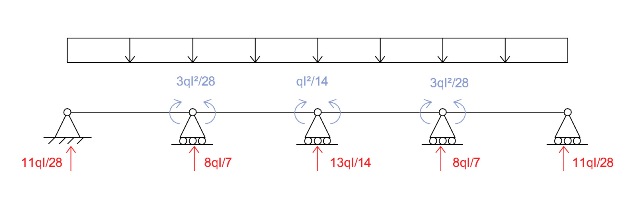
5)DISEGNO i diagrammi del TAGLIO e del MOMENTO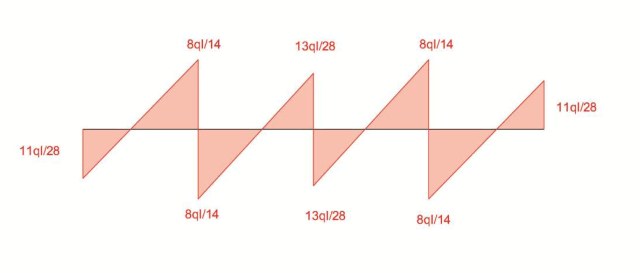

Commenti
francesca.secci
Mer, 17/04/2013 - 21:41
Collegamento permanente
Risoluzione di una struttura
Risoluzione di una struttura iperstatica attraverso il METODO DELLE FORZE
Ho una struttura 3 volte iperstatica
La risolvo con il metodo delle forze
1)Definisco la STRUTTURA ISOSTATICA DI RIFERIMENTO ⁴²
⁴²
2)EQUAZIONI di COMPATIBILITÁ CINEMATICA
Δϕ(B)=0
ma dato che la struttura è simmetrica sappiamo che Δϕ(B)= Δϕ(D)=0
PUNTO B
ϕ(Bs)=ql³/24EI-X₁l/3EI
ϕ(Bd)=-ql³/24EI+X₁l/3EI +X₂l/6EI
PUNTO C
ϕ(Cs)=ql³/24EI-X₂l/3EI- X₁l/6EI
ϕ(Cd)=-ql³/24EI+X₂l/3EI +X₁l/6EI
ϕ(Bs)= ϕ(Bd) ql³/24EI-X₁l/3EI=-ql³/24EI+X₁l/3EI +X₂l/6EI
X₁=ql²/8- X₂/4
ϕ(Cs)= ϕ(Cd) ql³/24EI-X₂l/3EI- X₁l/6EI=-ql³/24EI+X₂l/3EI +X₁l/6EI
X₂= ql²/8- X₁/2
Andando poi a sostituire X₁=ql²/8- X₂/4 in X₂= ql²/8- X₁/2 X₁=3ql²/28
E poi X₁=3ql²/28 in X₂= ql²/8- X₁/2 ottengo X₂=ql²/14
3)CALCOLO DELLE REAZIONI VINCOLARI
Trovate le incognite iperstatiche procedo con il calcolo delle reazioni vincolari applicando il principio di sovrapposizione degli effetti.
STRUTTURA CONSIDERANDO IL CARICO q
STRUTTURA CONSIDERANDO X₁,X₂
4)SOMMO LE REAZIONI VINCOLARI
5)DISEGNO i diagrammi del TAGLIO e del MOMENTO