blog di AlessandroValentini

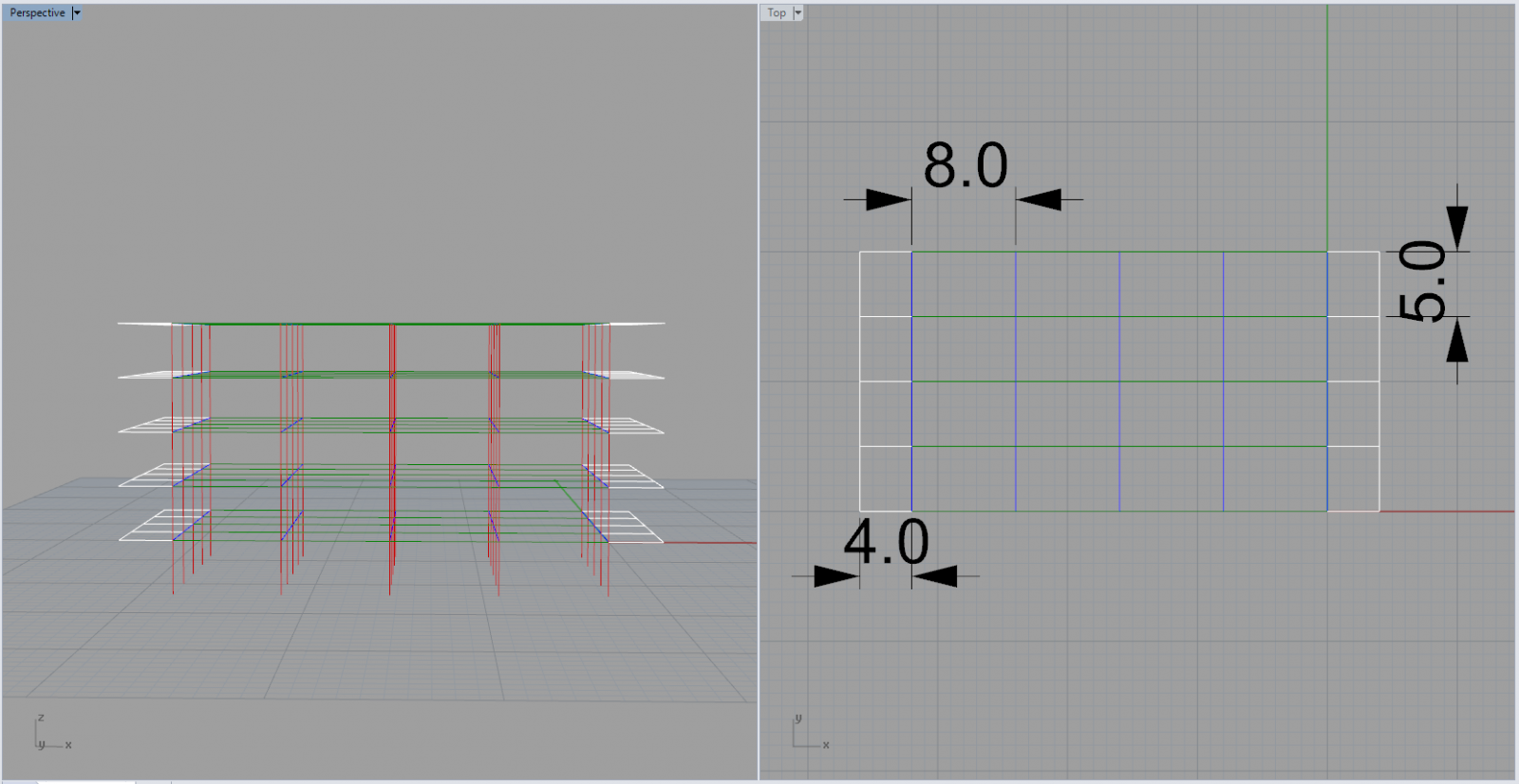
Si definisce una struttura a telai piani con la luce maggiore di 8m, la minore di 5m ed uno sbalzo di 4m sui lati corti; l’interpiano è di 4m.
Mentre il carico strutturale Qs sarà definito volta per volta,
 il carico permanente Qp è fissato a 3,05kN /mq composto sta:

• 0,5 kN/mq da impianti 
• 1kN/mq di tramezzi
• 0,5 per una finitura di ardesia
• 1 per il massetto
• 0,05 per un isolante

Qa è dato da normativa a 3kN/mq per gli uffici aperti al pubblico.

ACCIAIO

TRAVE
Si parte con la definizione dei travetti, orditi sul lato lungo e con interasse di 1m. Questi devono quindi sopportare un carico Qs definito da un solaio in acciaio composto da lamiera grecata con riempimento in calcestruzzo, mentre Qp e Qa fissi a 3,05 kN/mq e 3 kN/mq.
Si ricerca quindi il peso del solaio scelto, ritrovando un valore di 1,86kN/mq.

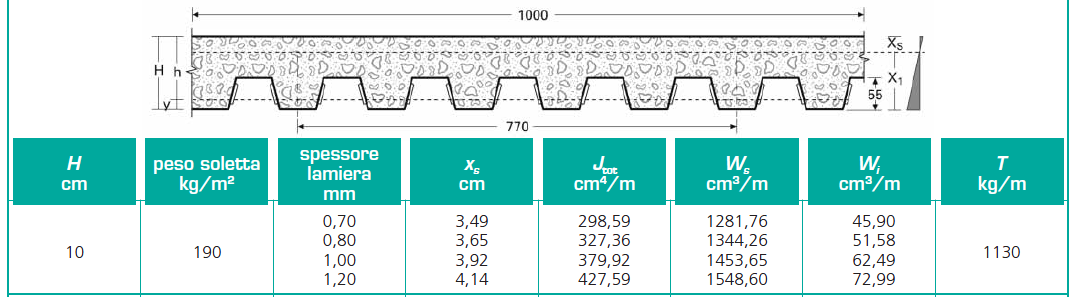
Si inseriscono quindi i valori nel foglio di calcolo e, ricercando nella tabella dei profilati IPE, si stabilisce un IPE 270 per i travetti.

A questo punto si definisce la trave più sollecitata dove i carichi restano i medesimi ma con l’aggiunta del peso del travetto. Con l’aiuto della tabella si stabilisce che la trave adatta risulta essere una IPE 500.

PILASTRO
Si determina il pilastro più sollecitato, ovvero uno centrale con un’area in influenza di 8m x 5m.

Si inseriscono i dati inerenti le luci e il peso delle travi, successivamente il peso del solaio, dato dalle tre componenti moltiplicato per i coefficienti da normativa. Si inserisce il numero di piani e il tipo di acciaio usato, un 235. Per tener conto della presso-flessione si divide l’fyd per due, di modo da avere già un’indicazione di massima. L’ultimo dato importante da mettere è il beta, fissato a 0,8 tenendo conto dell’incastro a terra. I dati che si ottengono orientano la scelta del profilo di acciaio, un HEA 450.
MENSOLA
Si ripete il procedimento analogo con la mensola, la quale ha una luce di 4m e dei carichi analoghi alle travi principali.
Inserendo il momento di inerzia resistente di una IPE 500 si vede che l’abbassamento risulterebbe circa 1/350 della luce; si prova quindi ad inserire il valore di una IPE 450, constatando come l’abbassamento massimo risulta ancora inferiore all’ordine del 200. Poiché una IPE 400 restituirebbe un valore maggiore, si determina la 450 come soddisfacente.

CALCESTRUZZO

TRAVE
Nel caso del calcestruzzo, il solaio scelto è un tipo predalles, come da figura. Il carico strutturale è quindi dato dai pesi specifici a mc dei singoli materiali moltiplicati per le loro dimensioni e per l’interasse. Si ottiene quindi: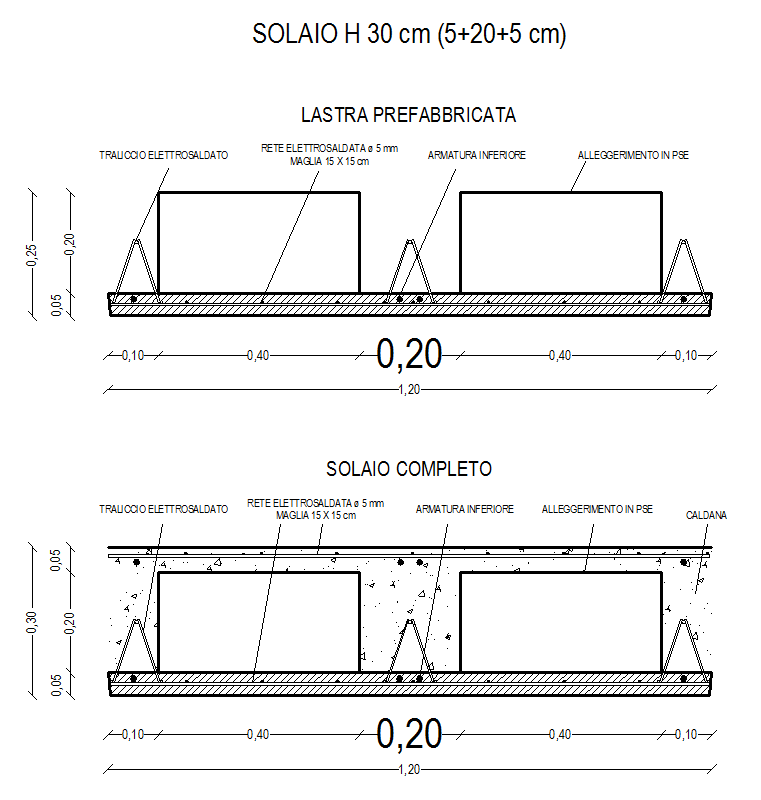

• 0,013 kN/mq alleggerimento
• 1,66 kN/mq travetti
• 1,25 kN/mq (x2) calcestruzzo superiore e inferiore.
  Qs = 4,173 kN/mq  - Qp = 3,05 kN/mq -  Qa = 3kN/mq

  Il procedimento risulta essere pressoché il medesimo; l’unica accortezza è quella di prendere i valori della riga inferiore in quanto qui essi tengono conto anche del peso proprio della trave che, nel caso del calcestruzzo, risulta essere un carico non indifferente.

PILASTRO
Nel caso del pilastro, una volta inseriti i valori bisogna giocare con i valori di base e altezza della sezione: colpa anche la classe non particolarmente performante presa, se si prendono dei valori nell’immediato intorno dei valori minimi suggeriti dal foglio di calcolo si ottiene una tensione massima nella sezione che supera il valore massimo sopportabile dal materiale. In tal caso, sebbene bmin e hmin si attestino su 40 e 25cm, la sezione definitiva del pilastro è stata fissata ad un quadrato di lato 65cm, questo anche per evitare di avere valori di resistenza che differissero di molto sulle due coordinate.

 MENSOLA
 

LEGNO
TRAVE
Si definisce un solaio in legno con un Qs di 1,11Kn/mq, derivante dalla somma di un tavolato del peso di 0,11Kn/mq per un legno di conifere e di un massetto di allettamento del peso di 1Kn/mq.
Si ricava quindi la dimensione necessaria dei travetti e delle travi principali, prendendo come materiale un legno di classe C18 di conifera.

PILASTRO

MENSOLA

Consegna 1_ Reticolare Stellata

Parto con la definizione della struttura, un quadrato di lato 20m incernierato ai quattro angoli e centralmente e uno sbalzo di ulteriori 5m su tutto il perimetro per una dimensione totale di 25m.
Scelgo quindi un modulo base per la reticolare costituito da un quadrato di lato 5m e altezza 2m: questo significa che la diagonale arriva ad una lunghezza di 5,39 che andrà a determinare la mia luce libera di inflessione di partenza.  
 

Stabilisco quindi un l₀=5,5 con un ß =1 considerata la natura a cerniera dei due vincoli all’estremità. Da qui definisco un ρ_min da normativa di 2,75 (550/200) e, da sagomario, opto per un tubolare cavo di dimensioni 88,9mm con 2,6mm di spessore interno.           

Disegno la struttura su Rhinoceros con il desiderio di creare una struttura simmetrica sui due assi principali.
Importo la struttura su SAP e definisco tutte le travi della mia struttura per un totale di 532elementi.
Da qui inizio con il definire la sezione, stabilita in precedenza, e assegnandola a tutti gli elementi. Inserisco i cinque vincoli nelle posizioni già determinate e rilascio la torsione alla fine e i momenti a entrambe le estremità.
Faccio partire un’analisi preliminare dalla quale mi esporto le tabelle, constatando che il peso della struttura si attesta sui 103,064KN.

Continuo con la definizione dei carichi puntuali stabilendo il carico totale che la struttura andrà a sopportare. Avendo un’area di 900mq e ipotizzando 3 solai ottengo un’Atot di 2700mq che, moltiplicati per 10KN a mq significa un carico di 27'000 KN*mq; sommando a questo il peso proprio della struttura ottengo 27'103,064KN. Divido ora il carico complessivo per i mq di un solo piano -> 27'103,064KN/900mq=30,115KN/mq. 

 
Ora distinguo i tre casi di carico nei nodi, ovvero il caso dei nodi centrali, i quali si fanno carico di un’area di 25mq, i nodi perimetrali – 12,5mq – e i nodi angolari, sui quali si scarica una forza concentrata pari ad un’area di 6,25mq.     
 

 Ottengo quindi

Caso 1 - 30,115KN/mq*25mq=752,8629KN
Caso 2 - 30,115KN/mq*12,5mq =376,431KN
Caso 3 - 30,115KN/mq*6,25mq =188,21572KN

Visualizzo gli sforzi normali constatando come questi rispecchino la simmetria della struttura. Estraendo la tabella noto come i valori massimi si attestino su un valore di 4042,631 di Compressione e di 3437,898 di Trazione.