Progettazione Strutturale 1M - a.a. 2017/2018
prof.ssa Ginevra Salerno - studente: Antonio Tripodo [462841] con Francesco Varano [475968]
Seconda Esercitazione: Dimensionamento di un telaio in tre tecnologie – Parte 2
Vento
L’azione del vento sulla struttura è descrivibile attraverso un andamento (co)sinusoidale in quanto agente naturale variabile. La NTC 2008 consente di studiare l’intensità di questo fenomeno attraverso la formula della Pressione Cinetica di riferimento
P = 0,5 ρ(v)^2
nella quale P rappresenta la pressione esercitata dal vento sull’edificio [N/m^2], ottenuta dal prodotto di ρ (valore di densità dell’aria = 1,25 Kg/m^3) e il quadrato di v (velocità di riferimento del vento, calcolata in m/s).
Per una analisi di massima consideriamo un apporto di 0,4 KN/m^2 sulla facciata controvento e 0,2 KN/m^2 sulla facciata sottovento, valori moltiplicati per l’area di influenza dei rispettivi pilastri perimetrali.
Sisma
L’azione sismica viene descritta come un carico linearmente distribuito, crescente con l’altezza dell’edificio, e calcolata per ogni livello attraverso le formule
Fi = Fs (zi Wi / Szi Wi)
Fs = cW
dove Fs rappresenta l’intensità del sisma ed è ottenuta dal prodotto di c (rapporto fra l’accelerazione sismica e quella gravitazionale = 0,3 per questa zona) e W (la somma del peso strutturale, il 20% di un eventuale Carico Neve e il 30% dei Carichi di Destinazione). Questa viene a sua volta moltiplicata per il rapporto fra il prodotto del livello considerato con la sua W e la sommatoria di prodotti fra i vari livelli dei piani e i loro rispettivi W.
Se l’interpiano rimane costante per tutto l’edificio il calcolo di Fi si limita al prodotto di Fs e il rapporto fra il livello del piano considerato e la somma dei livelli di ogni piano.
z =interpiano (costante), 4 piani
F1 = Fs (z/10z) = Fs/10
F2 = Fs (2z/10z) = Fs (2/10)
F3 = Fs (3z/10z) = Fs (3/10)
F4 = Fs (4z/10z) = Fs (4/10)
Il sisma nella realtà si concentra in un unico punto dell’edificio, detto Centro di Massa, vicino ma non corrispondente al baricentro geometrico della struttura. Per l’analisi su SAP2000 vengono individuati più punti, ciascuno situato nel Centro di Area di Impalcato di ogni piano.
Nel caso in cui la geometria del piano non fosse regolare, le sue coordinate vengono calcolate attraverso la formula
C(Xc, YC)
Xc = x1(A1) + x2(A2) / (A1 + A2)
Yc = y1(A1) + y2(A2) / (A1 + A2)
altrimenti il Centro di Area coincide con il baricentro geometrico del piano. Questo punto costituisce una prosecuzione del vincolo interno Diaphram.
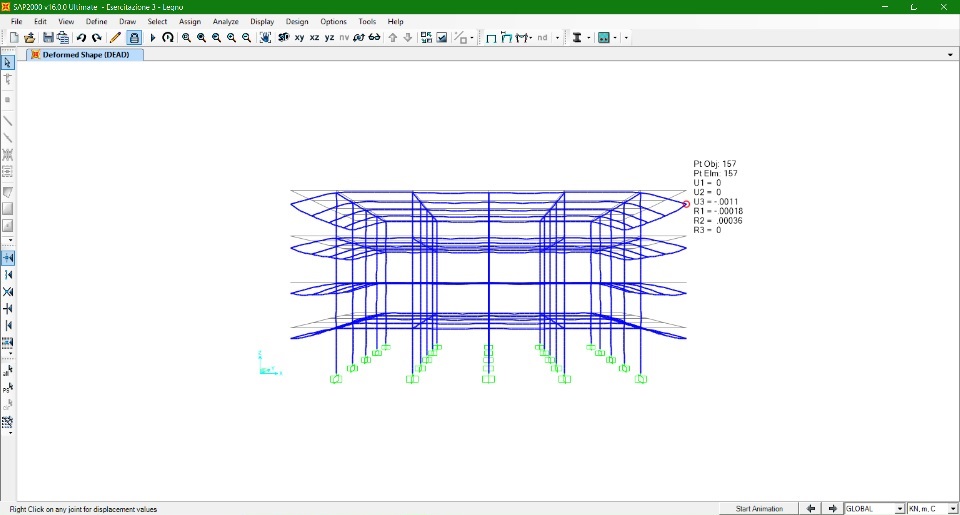
Si procede con la verifica della risposta dei tre modelli di telaio sottoposti ad azioni combinate:
a) CARICO VERTICALE SLU e AZIONE VENTO dir. X
b) CARICO VERTICALE SLU e AZIONE VENTO dir. Y
c) CARICO VERTICALE SLU e AZIONE SISMA dir. X
d) CARICO VERTICALE SLU e AZIONE SISMA dir. Y
TELAIO IN ACCIAIO
Carico verticale SLU
Qs = 1,7 KN/m^2 (1,3) (5 m) = 11,05 KN/m
Qp = 2,635 KN/m^2 (1,5) (5 m) = 19,8 KN/m
Qa = 2 KN/m^2 (1,5) (5 m) = 15 KN/m
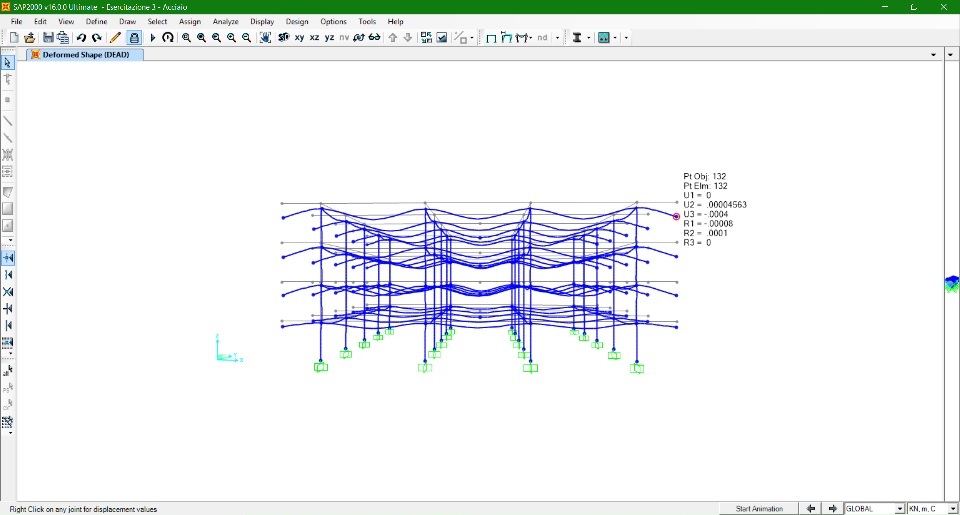
Azione Vento dir. X
Pilastro controvento
P = 0,4 KN/m^2 (5 m) = 2 KN/m
Pilastro sottovento
P = 0,2 KN/m^2 (5 m) = 1 KN/m
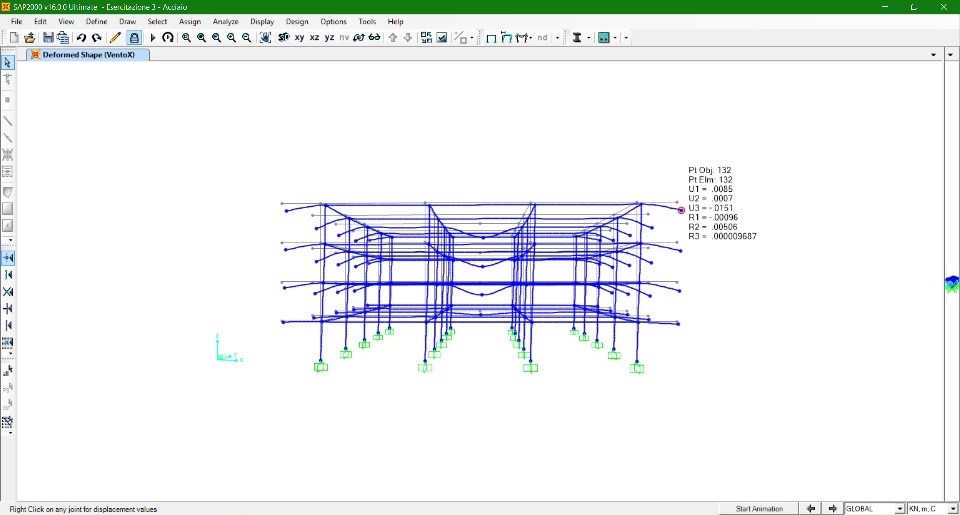
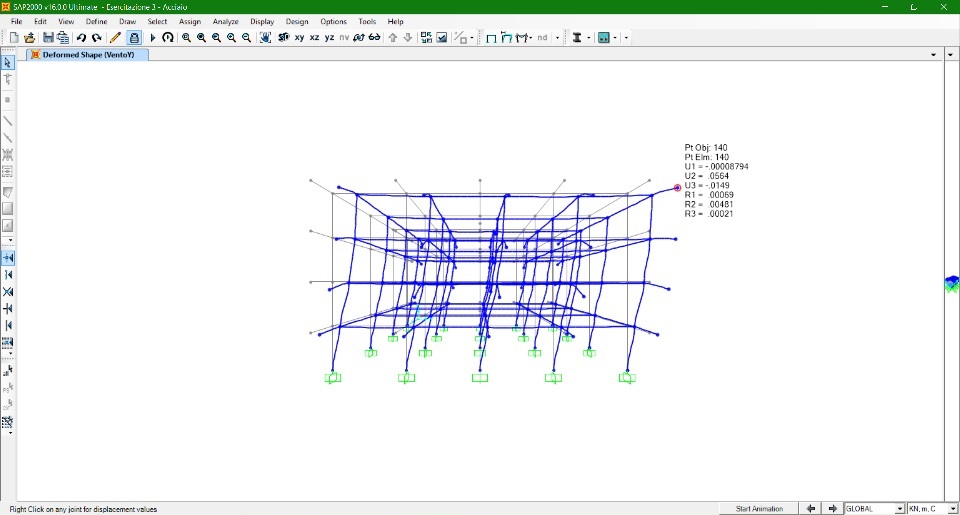
Azione Vento dir. Y
Pilastro controvento
P = 0,4 KN/m^2 (8 m) = 3,2 KN/m
Pilastro sottovento
P = 0,2 KN/m^2 (8 m) = 1,6 KN/m
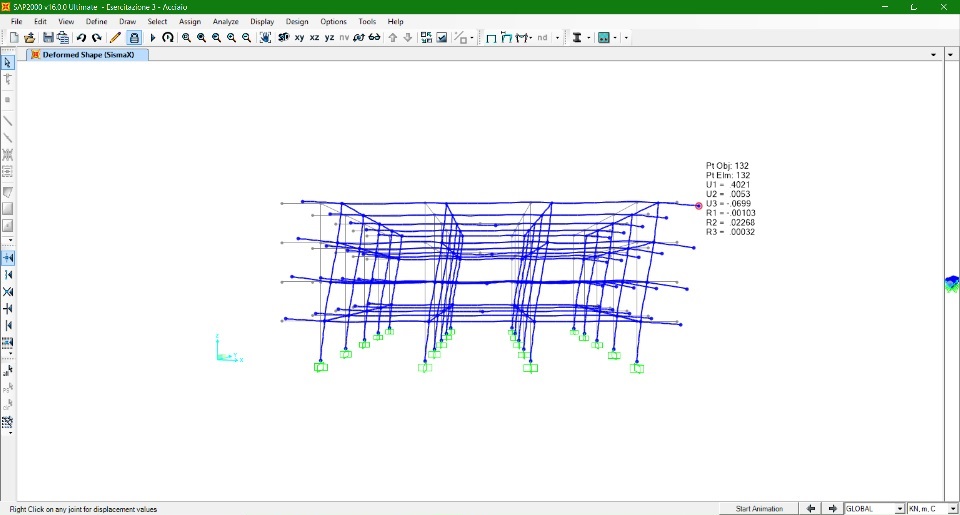
Azione Sisma dir. X e Y
Fs = (0,3) (15584,2 KN + 120 KN + 1440 KN) = 5143,26 KN
F1 = 514,33 KN
F2 = 1028,652 KN
F3 = 1542,99 KN
F4 = 2057,304 KN
C (15, 10)
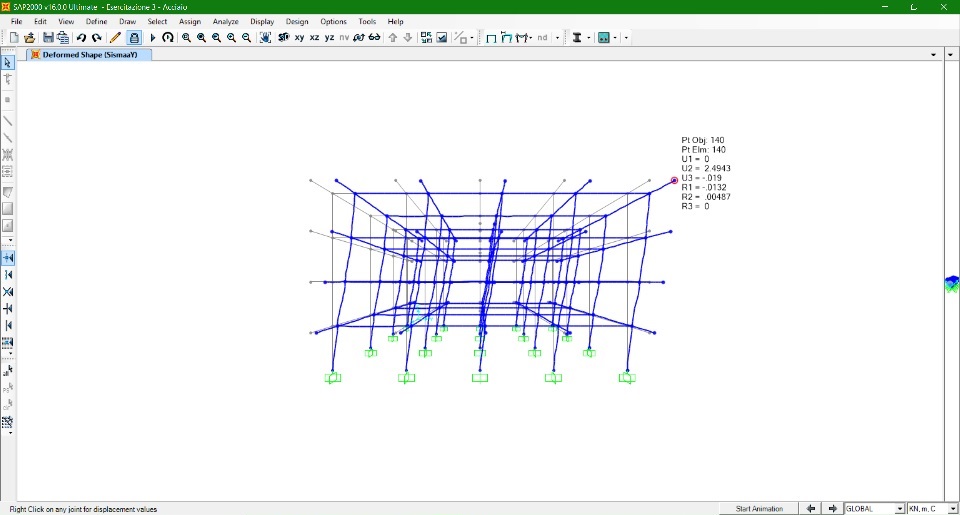
TELAIO IN CLS ARMATO
Carico verticale SLU
Qs = 3,21 KN/m^2 (1,3) (3 m) = 12,52 KN/m
Qp = 2,34 KN/m^2 (1,5) (3 m) = 10,53 KN/m
Qa = 2 KN/m^2 (1,5) (3 m) = 9 KN/m
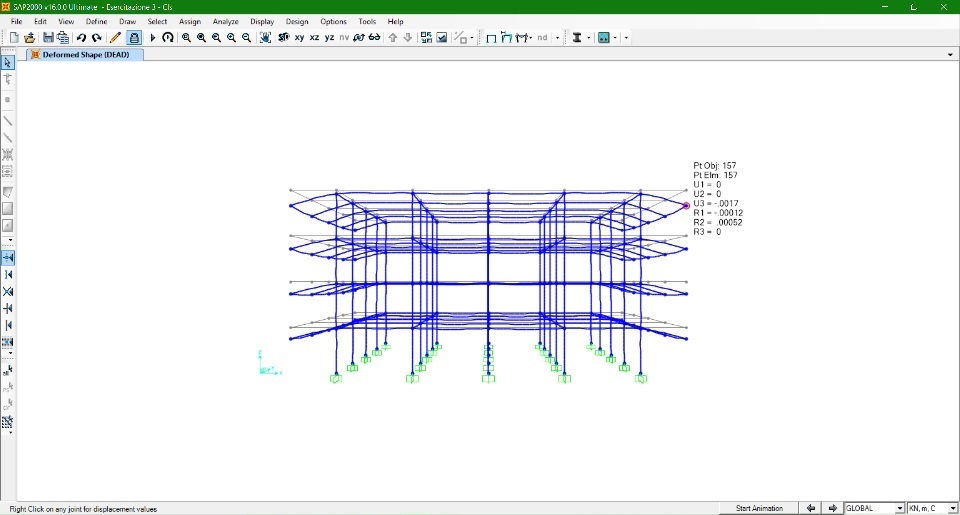
Azione Vento dir. X
Pilastro controvento
P = 0,4 KN/m^2 (3 m) = 1,2 KN/m
Pilastro sottovento
P = 0,2 KN/m^2 (3 m) = 0,6 KN/m
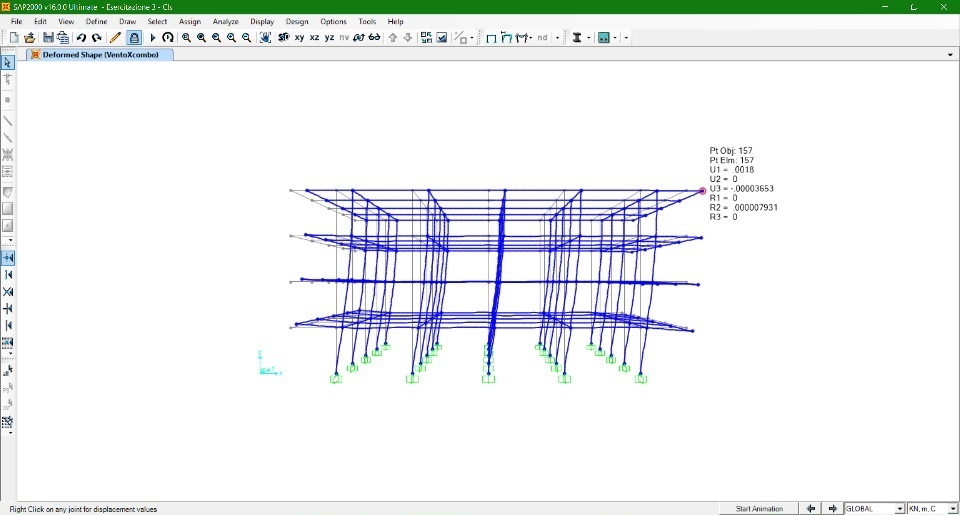
Azione Vento dir. Y
Pilastro controvento
P = 0,4 KN/m^2 (5 m) = 2 KN/m
Pilastro sottovento
P = 0,2 KN/m^2 (5 m) = 1 KN/m
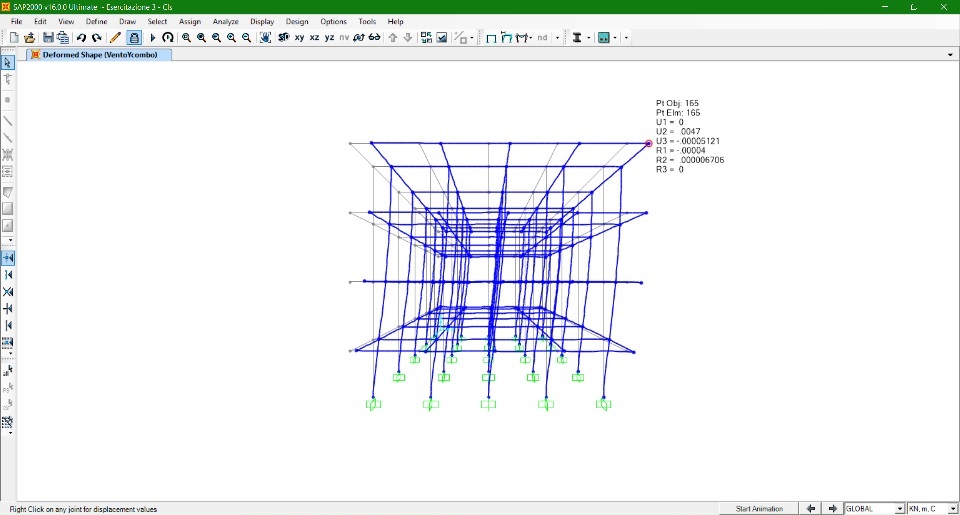
Azione Sisma dir. X e Y
Fs = (0,3) (12043,4 KN + 187,2 KN + 62,4 KN) = 3688 KN
F1 = 368,8 KN
F2 = 737,6 KN
F3 = 1106,4 KN
F4 = 1475,2 KN
C (13, 6)
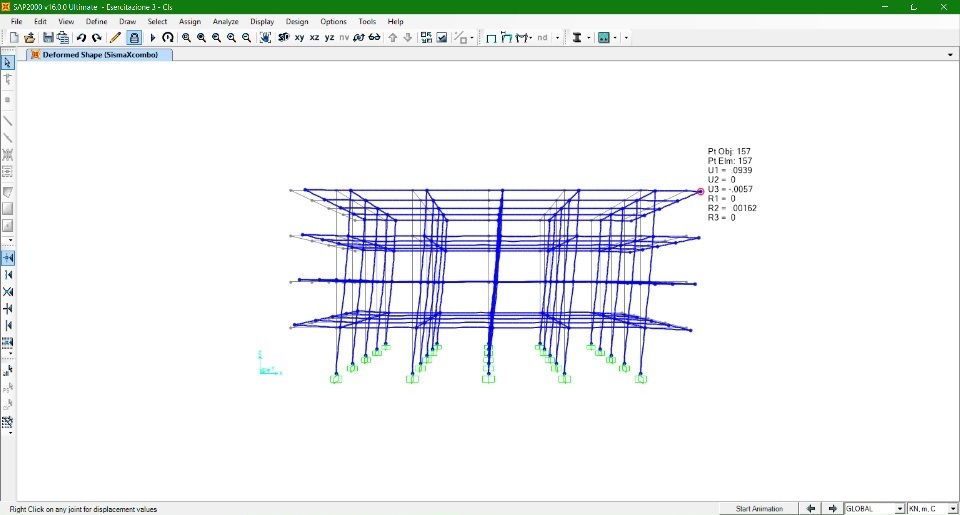
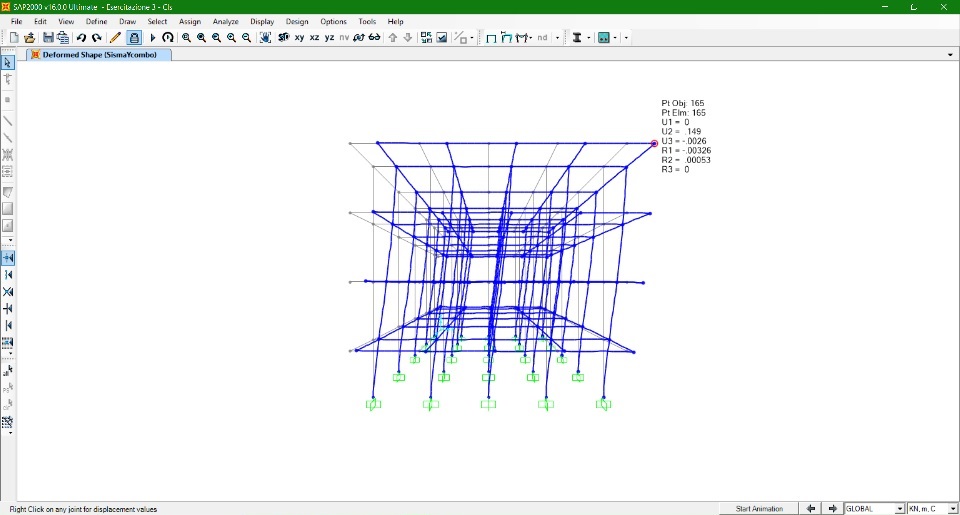
TELAIO IN LEGNO
Carico verticale SLU
Qs = 0,3562 KN/m^2 (1,3) (3 m) = 1,38918 KN/m
Qp = 2,635 KN/m^2 (1,5) (3 m) = 11,85 KN/m
Qa = 2 KN/m^2 (1,5) (3 m) = 9 KN/m
Azione Vento dir. X
Pilastro controvento
P = 0,4 KN/m^2 (3 m) = 1,2 KN/m
Pilastro sottovento
P = 0,2 KN/m^2 (3 m) = 0,6 KN/m
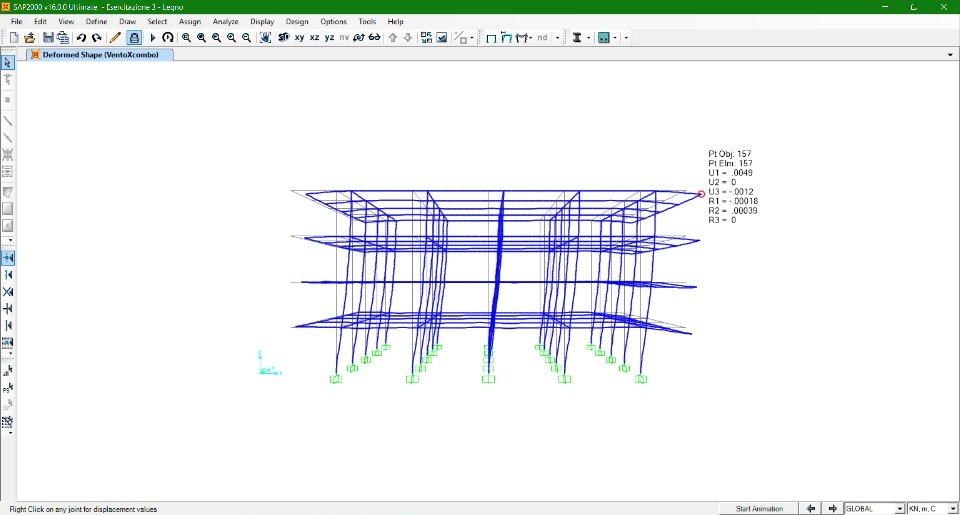
Azione Vento dir. Y
Pilastro controvento
P = 0,4 KN/m^2 (5 m) = 2 KN/m
Pilastro sottovento
P = 0,2 KN/m^2 (5 m) = 1 KN/m
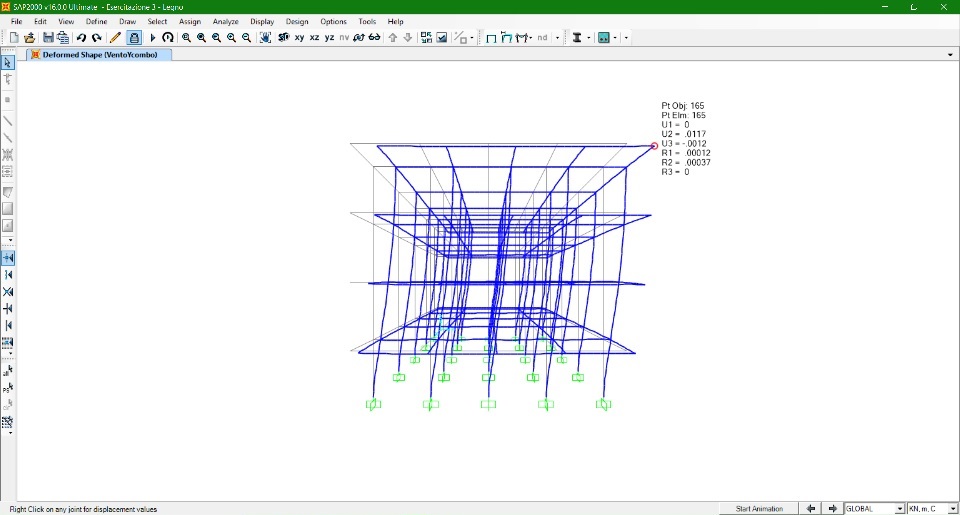
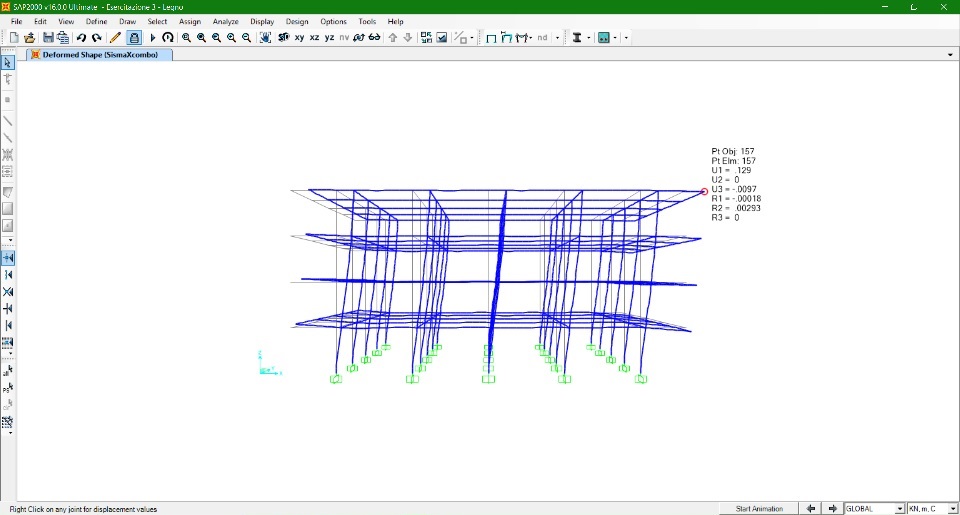
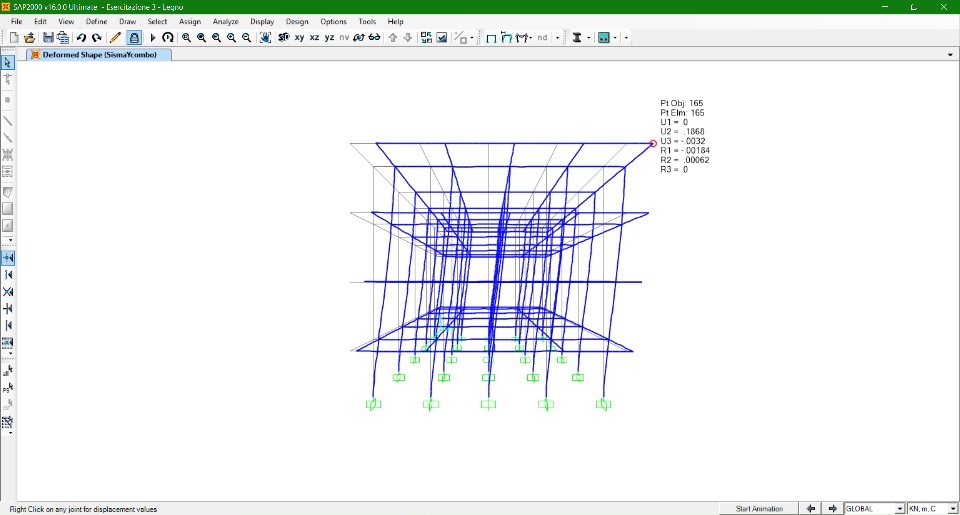
Azione Sisma dir. X e Y
Fs = (0,3) (5859,55 KN + 187,2 KN + 62,4 KN) = 1832,75 KN
F1 = 183,28 KN
F2 = 366,56 KN
F3 = 549,84 KN
F4 = 733,12 KN
C (13, 6)
Commenti recenti