INTRODUZIONE :
L’obiettivo di questa esercitazione è quello di studiare la struttura intelaiata in calcestruzzo armato di un edificio con inserimento di mensole e una gabbia scale centrale. Questo edificio si trova in zona non sismica, quindi analizzeremo i carichi verticali e le azioni del vento che influenzano l’edificio.

1 CARATTERISTICHE EDIFICIO:
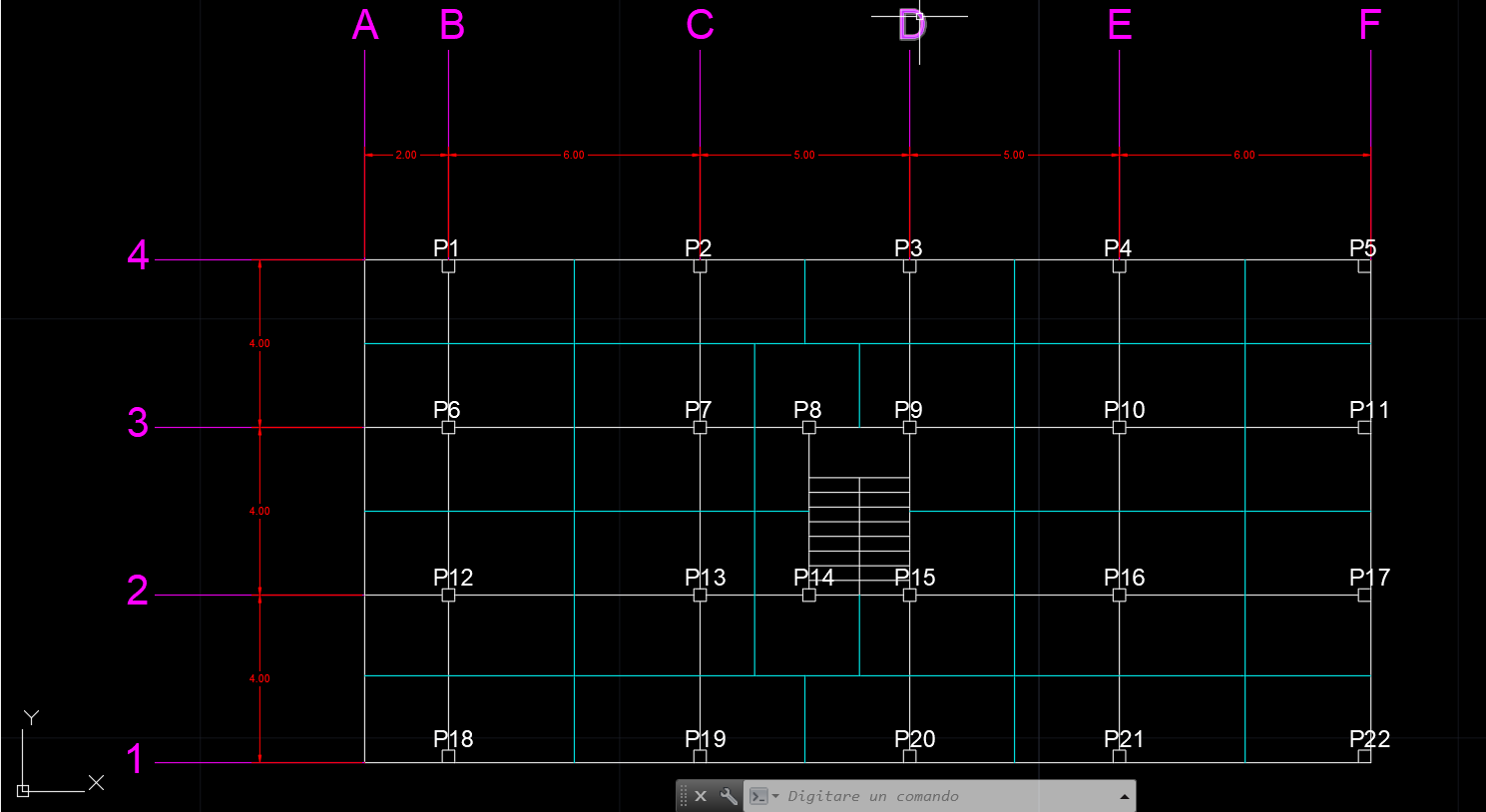
Edificio in calcestruzzo armato composto da 3 piani , con luci ordinarie e caratterizzato dalla presenza di aggetti, sul lato sinistro di 2 mt, e gabbia scale con trave a ginocchio, al centro dell’edificio.
Ogni piano ha 22 pilastri, quindi ci saranno 66 pilastri nell’edificio, divisi in 3 gruppi (centrali, perimetrali e angolari).
Per quanto riguarda gli elementi orizzontali, ci sono 3 gruppi: travi principali, travi secondarie e mensole.
2 COSTRUZIONE DEL MODELLO IN SAP:
iniziamo disegnando una campata di base, aiutandoci con il modello di griglia (Grid Only) che offre Sap .
Successivamente disegniamo i frame (travi e pilastri) . Per disegnare le altre campate utilizziamo il comando Draw Special Joints, stando attenti alla direzione degli assi globali.
Faremo quindi un offset dei punti in direzione x e con lo strumento Frame completeremo la campata.
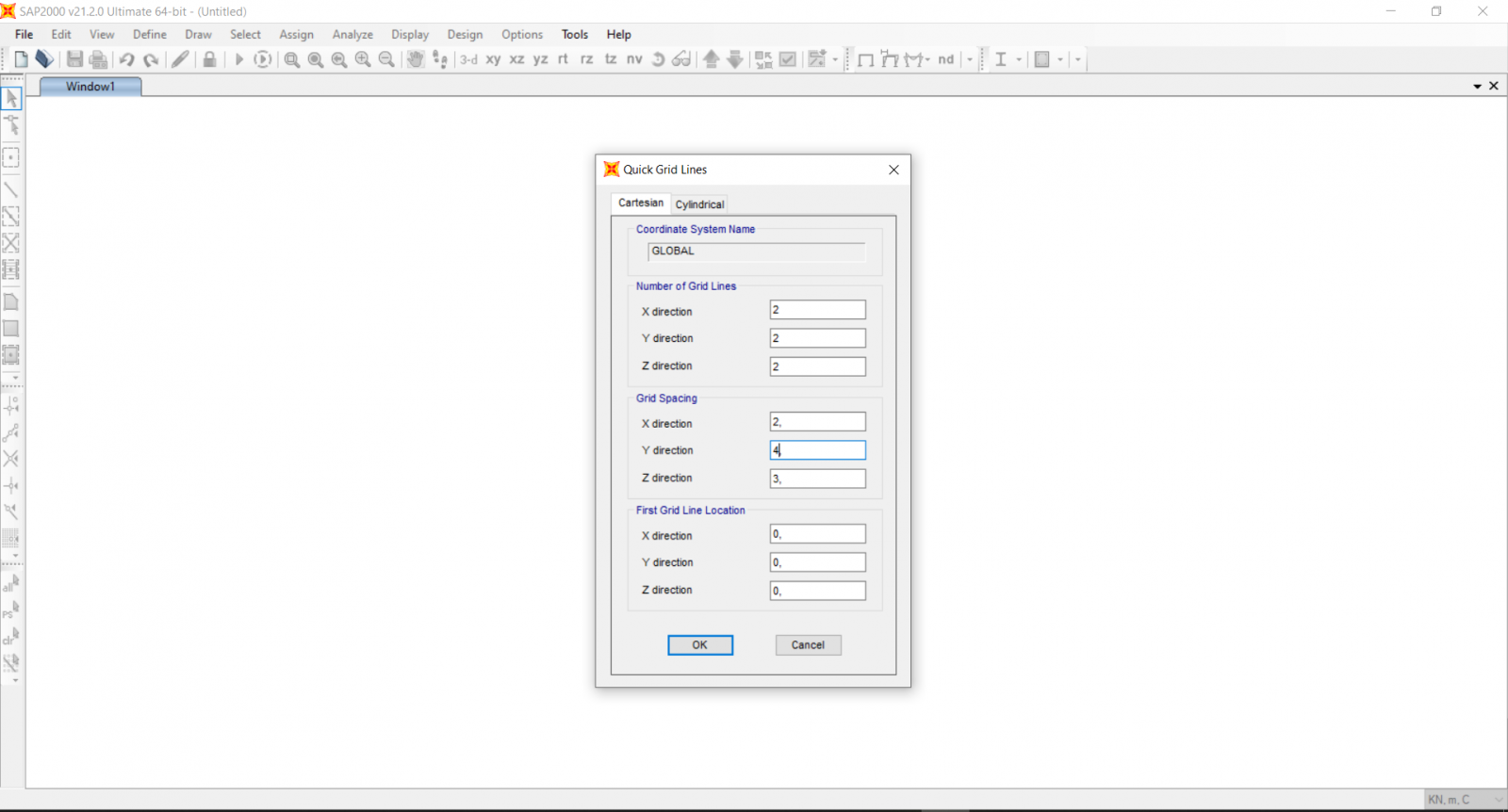
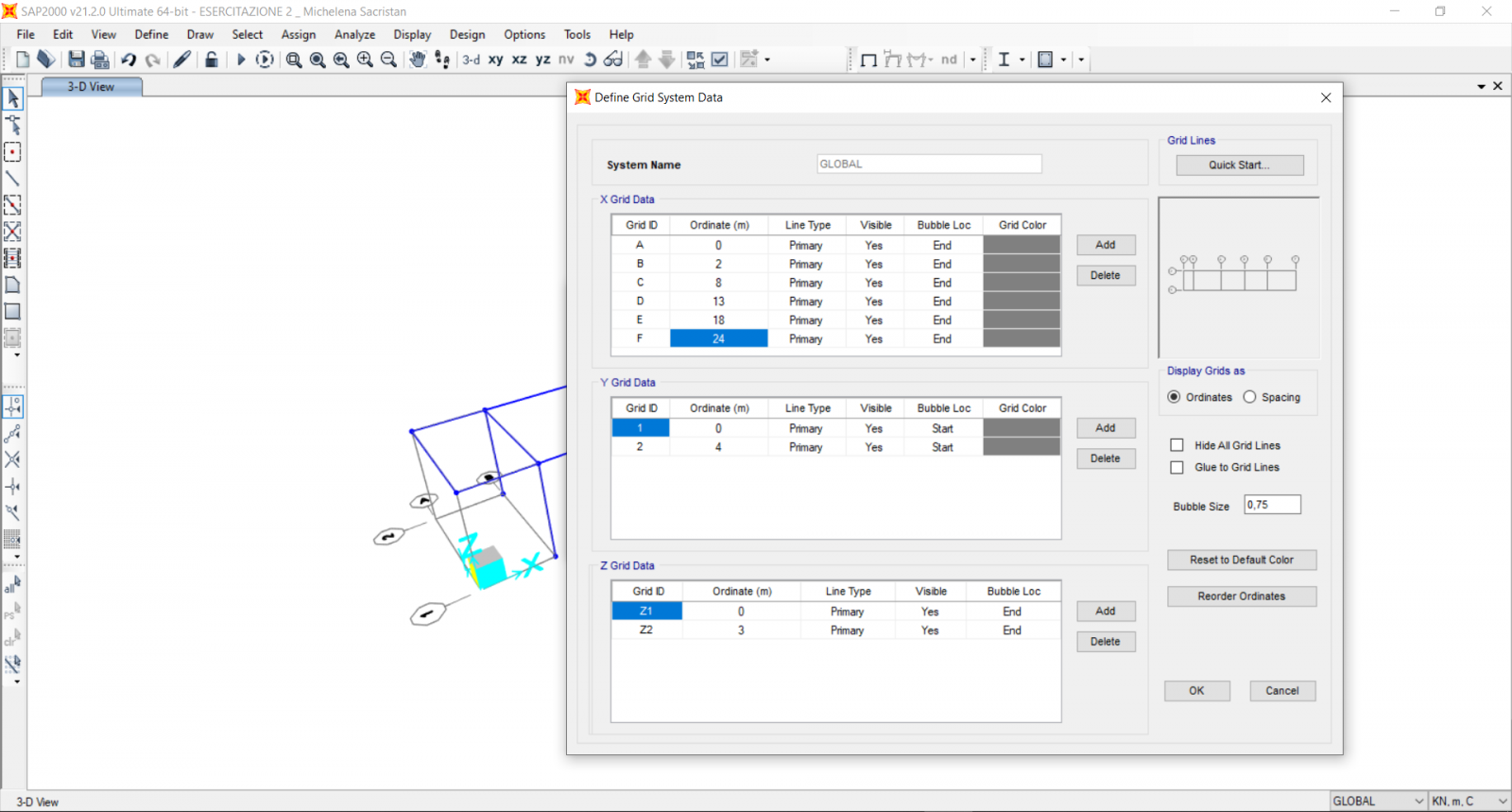
Modifichiamo ora la griglia per disegnare i pilastri mancanti : Edit Grid Data > Modify/Show System.
Inseriamo i valori che definiscono le linee di griglia con i quali identifico tutte le campate dell’edificio.
Dopo aver disegnato i pilastri mancanti, copiamo le campate disegnate per completare il piano terra dell’edificio. View>Set 3d view (si utilizza questo comando per semplificare le operazioni di selezione degli elementi).
Tasto rapido Ctrl+C – Ctrl+V > costruiamo così tutte le altre campate in direzione y .
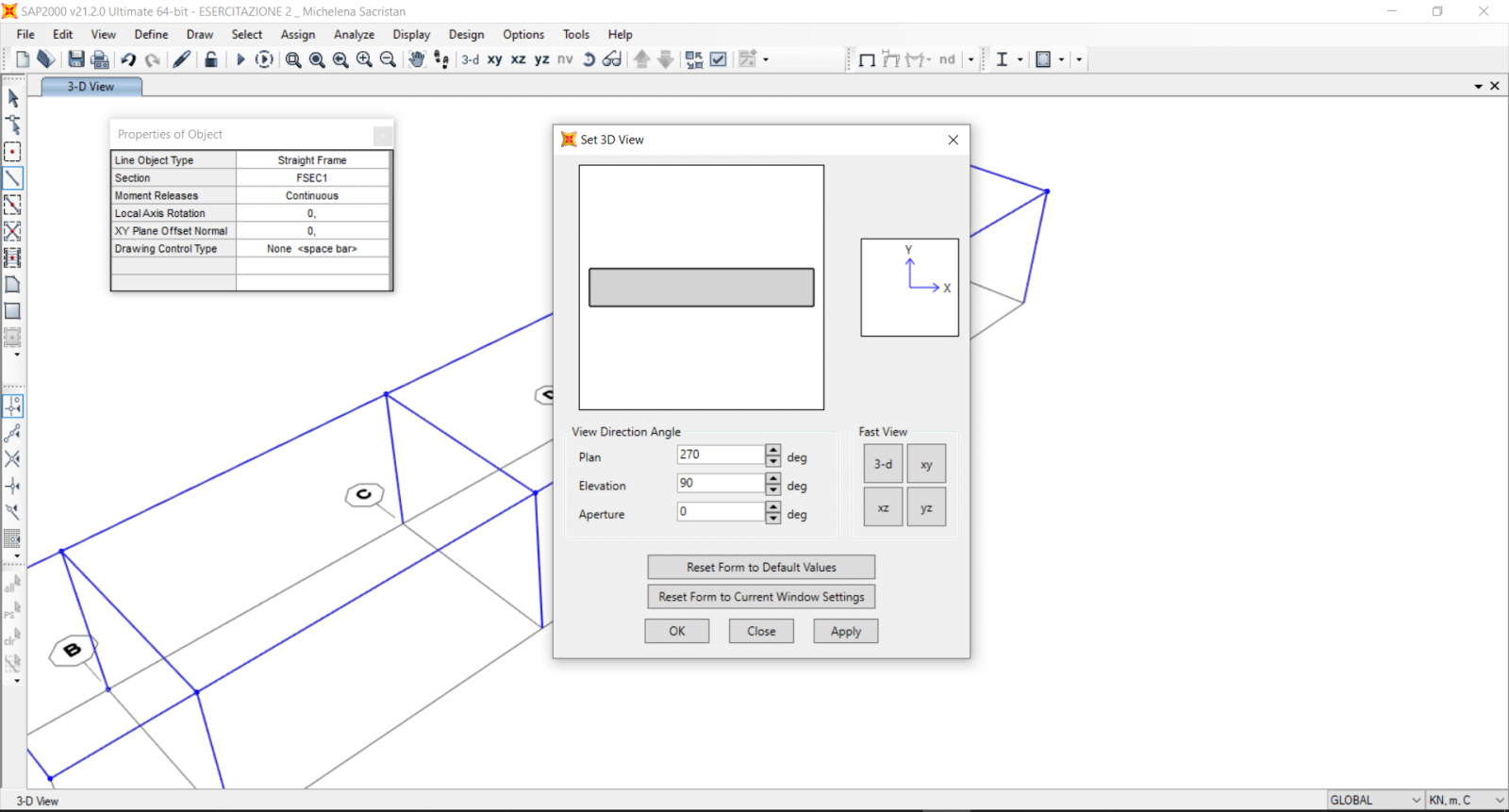
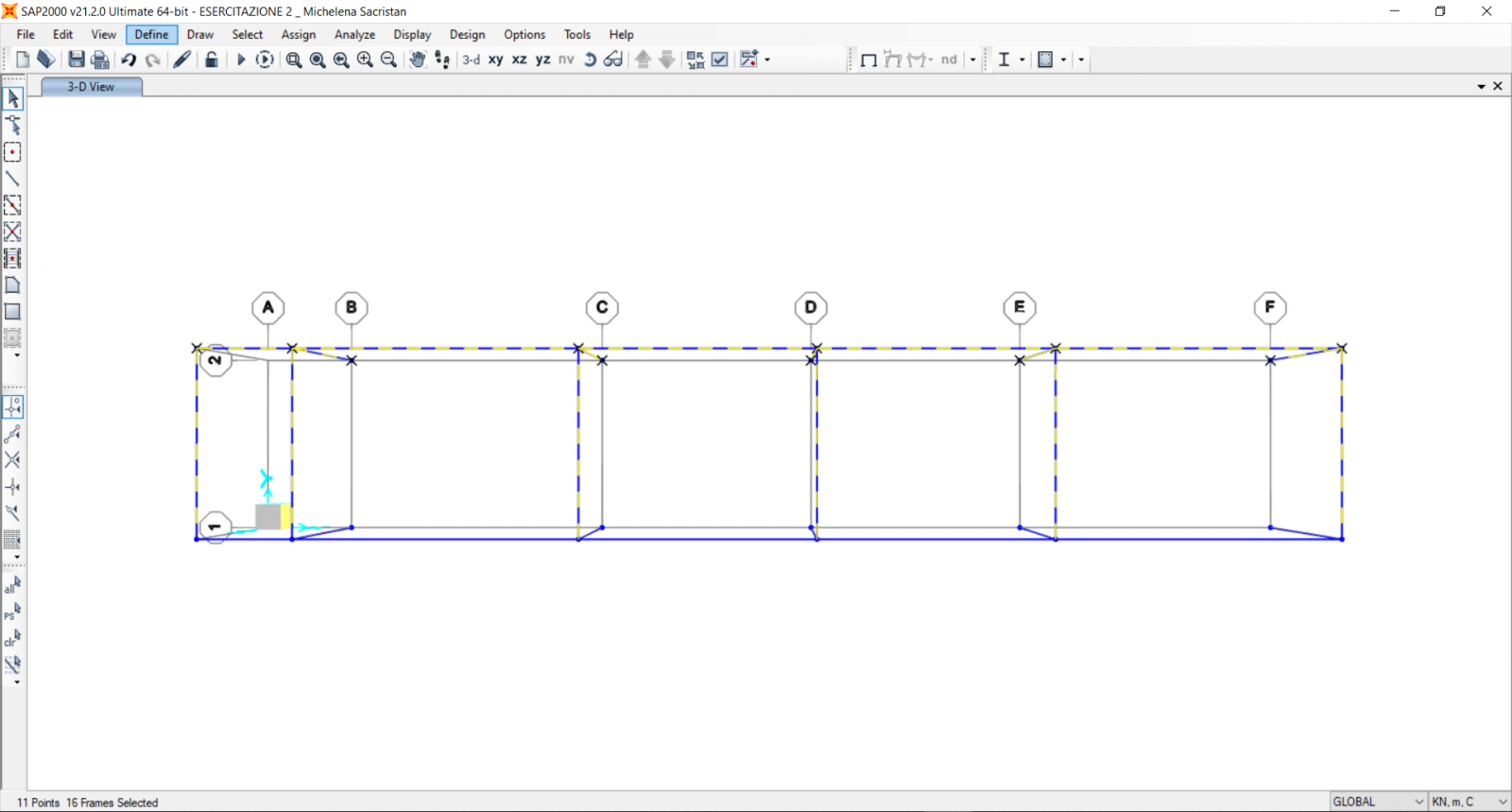
3 ASSEGNAZIONE DEI CARICHI:
Per l’assegnazione corretta dei carichi bisogna calcolare le aree di influenza di travi e pilastri .
Prenderemo in esame la trave più sollecitata (con area di influenza 6x4 mt). Per farlo utilizziamo il file xls “esercitazione travi” ma prima bisogna definire il materiale.
Define>Materials>Add new material> scegliamo cls 28/35 in quanto si tratta di una struttura ordinaria, in questo caso non abbiamo bisogno di un cls ad alte prestazioni).
Da qui fck = 28

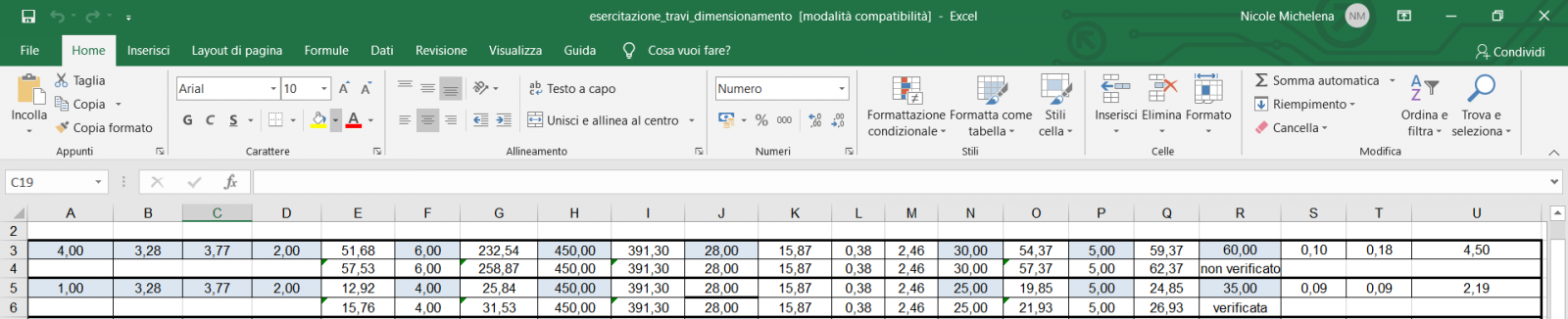
Nella tabella del file xls dedicato inseriamo i valori di Qs, Qp, Qa per arrivare a Qu (combinazione allo S.L.U.).
Qs = 3,28 kN/mq Qp = 3,77 kN/mq Qa = 2 kN/mq (residenziale)
Notiamo che il momento max è considerato con un valore pari a ql^2/8 , come fosse una trave doppiamente appoggiata. In questo caso prendiamo per buono comunque questo valore in quanto effettuiamo un primo dimensionamento di massima.
Inseriamo i valori di seguito :
fyk 450 (armature)
fck 28 (cls scelto)
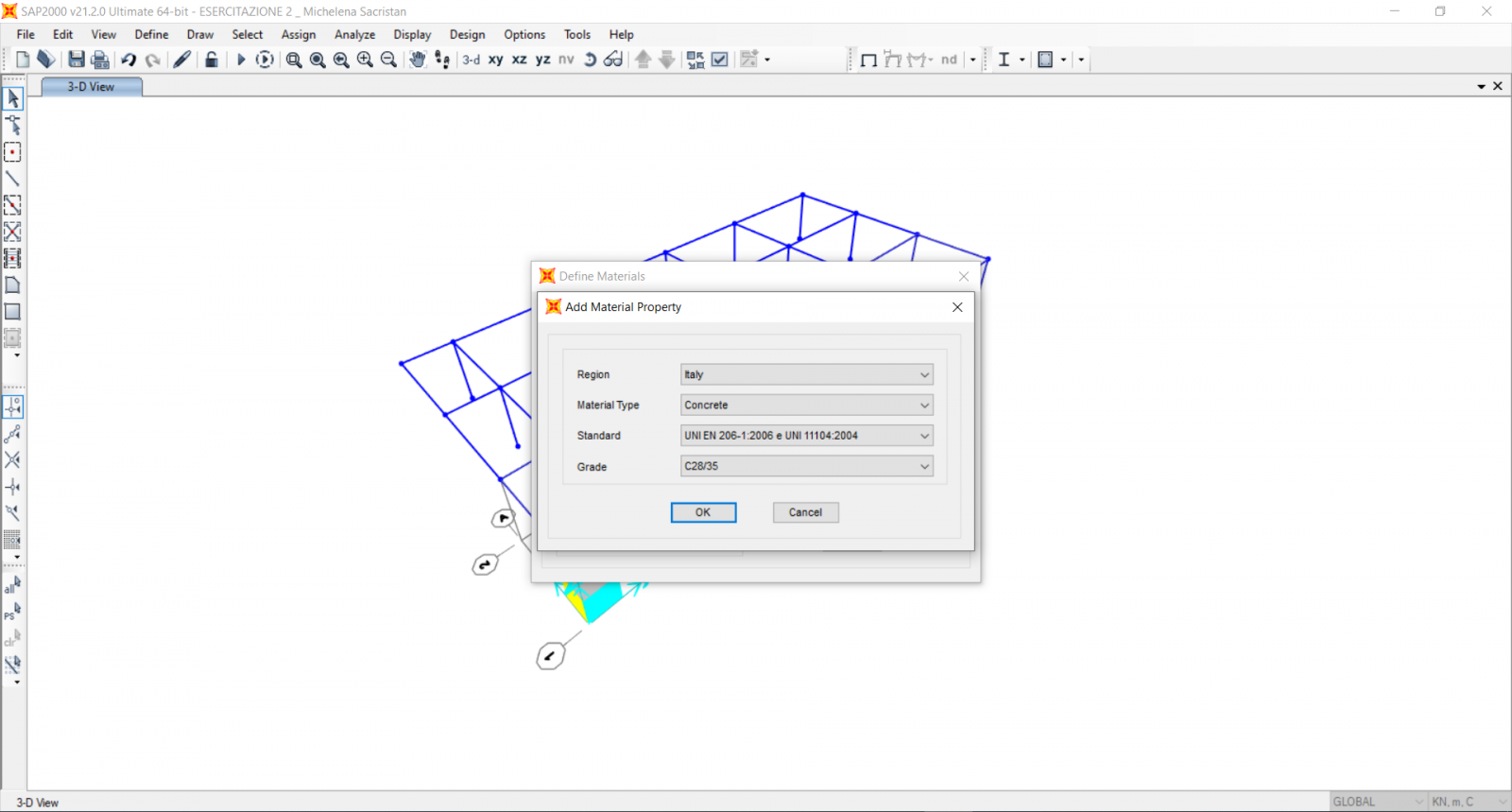

Scegliamo di considerare una trave b= 30 cm , H = 60 cm nonostante per ora non sia verificata, c’è da dire però che in questa prima riga di calcolo non si considera il PP della trave e il Mmax è calcolato in base al modello di trave doppiamente appoggiata, invece la nostra risulta essere continua.
4 DEFINIZIONE DELLE SEZIONI DA ASSEGNARE (DIMENSIONAMENTO DI MASSIMA) :
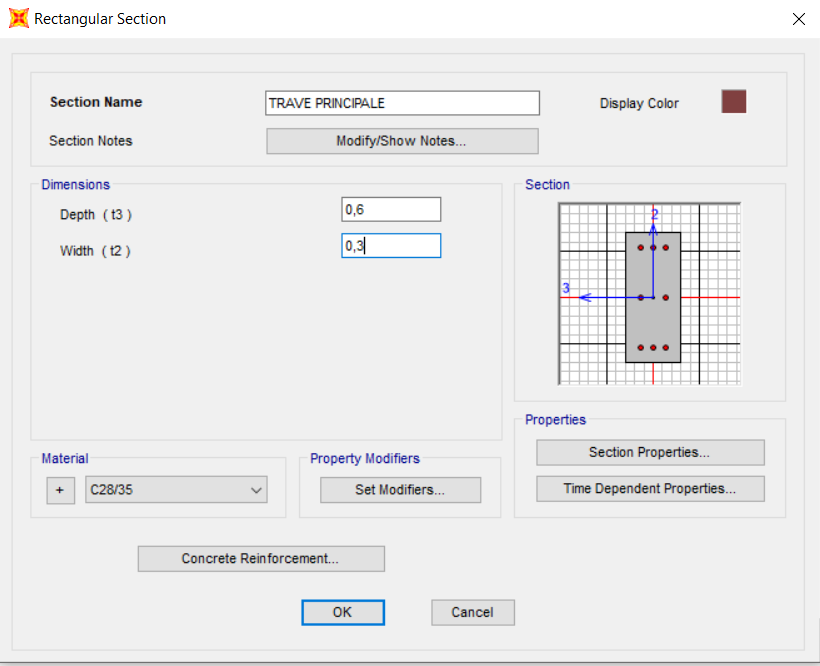
TRAVE PRINCIPALE
Possiamo ora definire una sezione per le travi principali usando i comandi Define>Section Properties>Frame Section>Add new property> concrete>rectangular. La rinominiamo “Trave Principale” e le assegnamo il materiale precedentemente scelto e le dimensioni della sezione.
TRAVE SECONDARIA:
Ripetiamo lo stesso procedimento calcolando una prima ipotetica sezione con il file xls dedicato .
Nota : sappiamo che , secondo la normativa vigente in materia (NTC 2018) , la trave secondaria avrà un’area di influenza di 50 cm per lato (tranne quella perimetrale).
Anche qui per effettuare una semplificazione consideriamo una unica sezione per le travi secondarie.
Queste travi sono anche dette di collegamento e portano un peso , ovviamente irrisorio rispetto a quelle principali).
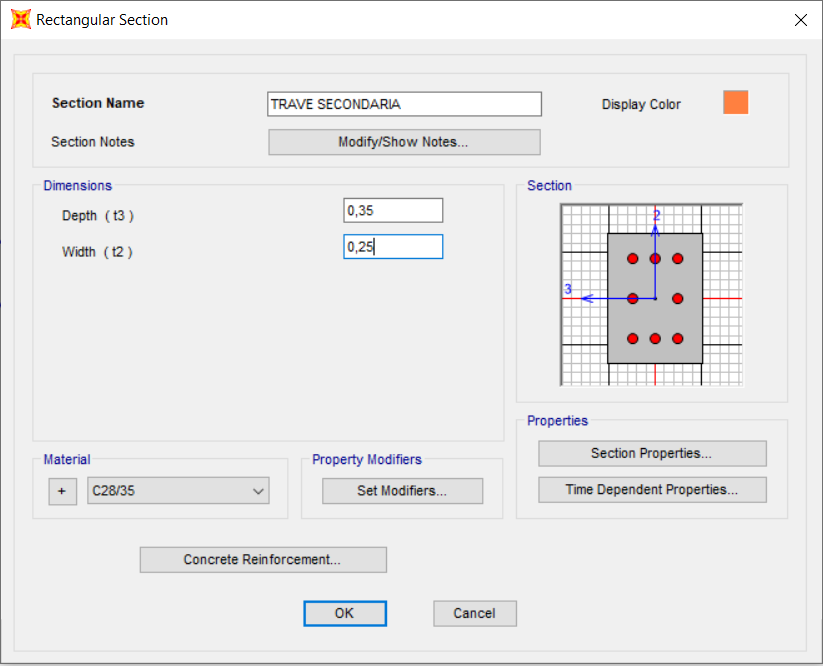
Scegliamo una trave con dimensioni :
b = 25 cm , H = 35 cm .
Ripetiamo quindi i passaggi su Sap per creare la sezione e assegnarla alle travi secondarie.
MENSOLA:
Calcoliamo l’area di influenza della mensola più sollecitata inserendo i valori nella tabella dedicata xls “mensole – deformabilità” .
Il Mmax in questa tabella è calcolato come se fosse un modello incastro e mensola a sbalzo = qL^2/2.
Per definire la sezione andremo in continuità con la trave principale facendo così una semplificazione nonostante nella realtà le mensole hanno una sezione maggiore dove si verifica il Mmax, e quindi in prossimità dell’incastro, e una sezione rastemata verso l’estremo libero dove il momento è = 0 . (nella realtà della costruzione le mensole hanno una sezione minima anche sull’estremo libero in quanto devono poter essere realizzate) .
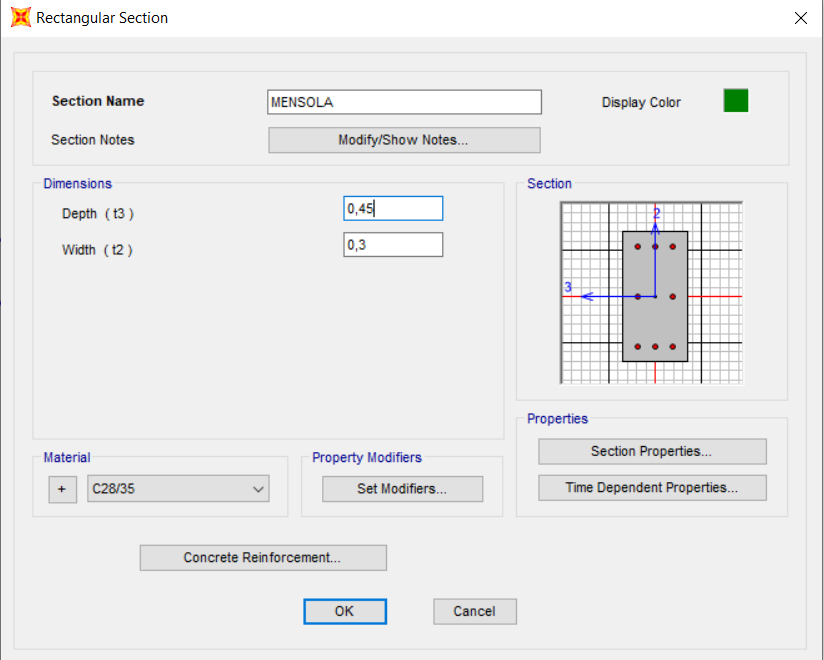
Avremo quindi b = 30 cm H= 45 cm .

Definiamo in Sap la sezione da assegnare alle mensole del nostro modello.
PILASTRI :
Esaminiamo il pilastro che ha l’area di influenza maggiore.
Calcoliamo il peso della trave al ml > 25 * 0,3 * 0,6 = 4,5 kN ml
Peso specifico della trave * area trave secondaria > 25 * 0,35 * 0,25 = 2,19 kN ml
Faremo questo procedimento per ogni piano dell’edificio, dato che N(kN) è la forza che agisce sui pilastri data dal carico del solaio, degli elementi strutturali (SLU) e moltiplicato per il n° piani .
Possiamo, in fase di predimensionamento di massima di non considerare il risultato della bmin dovuta alla snellezza del pilastro in quanto le luci sono ordinarie e i pilastri non sono più alti di 3 mt
Fck = 28 , E (modulo elastico cls 28/25) = 32208 Mpa
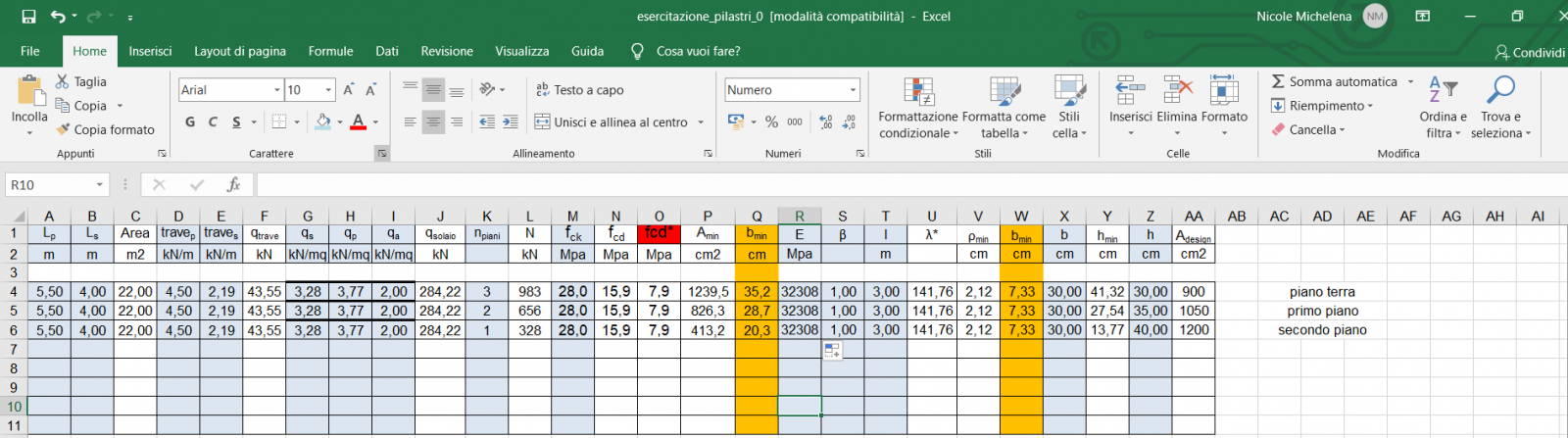
Nella colonna Q del file xls appaiono i valori sella sezione minima basati sullo sforzo normale .
E’ pur vero che nella realtà questi valori saranno inverosimili perché non stiamo considerando ancora la forza dovuta al sisma.
Dimensioneremo quindi i pilastri con una base più grande di quella richiesta.
(La sezione diventa più piccola man mano che si sale di piano e andrebbe fatta una distinzione tra pilastri perimetrali, centrali ed angolari).
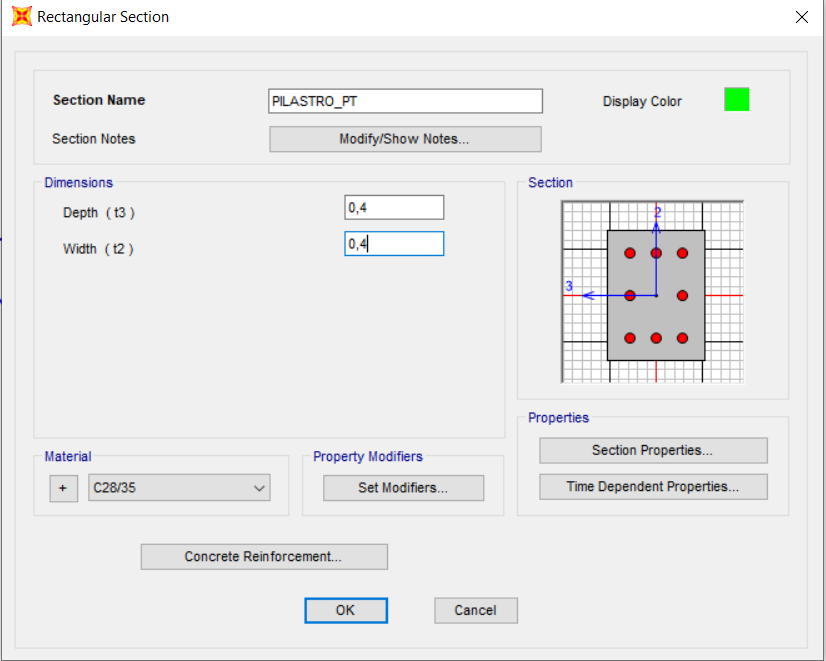
Definizione della sezione dei pilastri su Sap. Define >Section properties>Frame section >Add copy of property.
- PIL _ PT : 40 X 40 cm
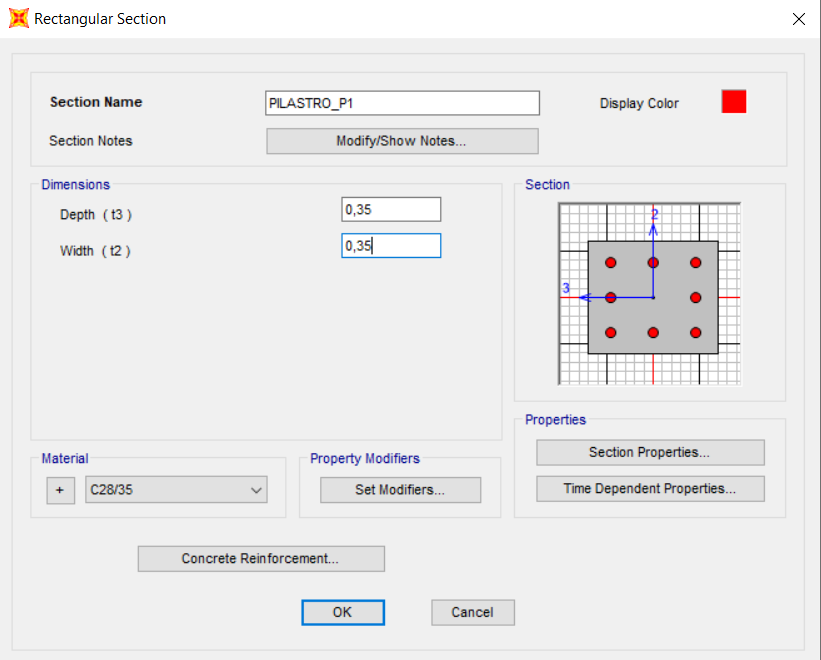
- PIL_ P1 : 35 x 35 cm
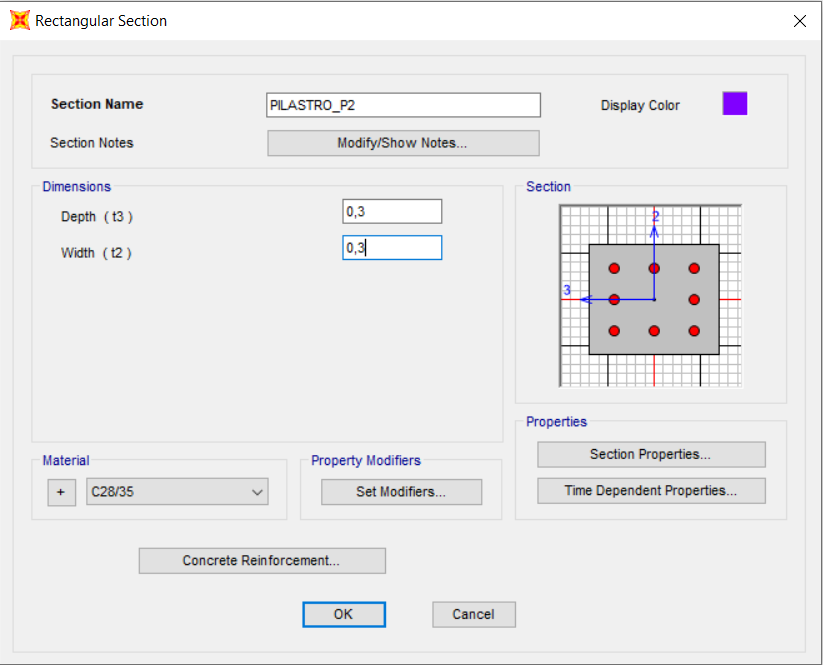
- PIL_P2 : 30 X 30 cm
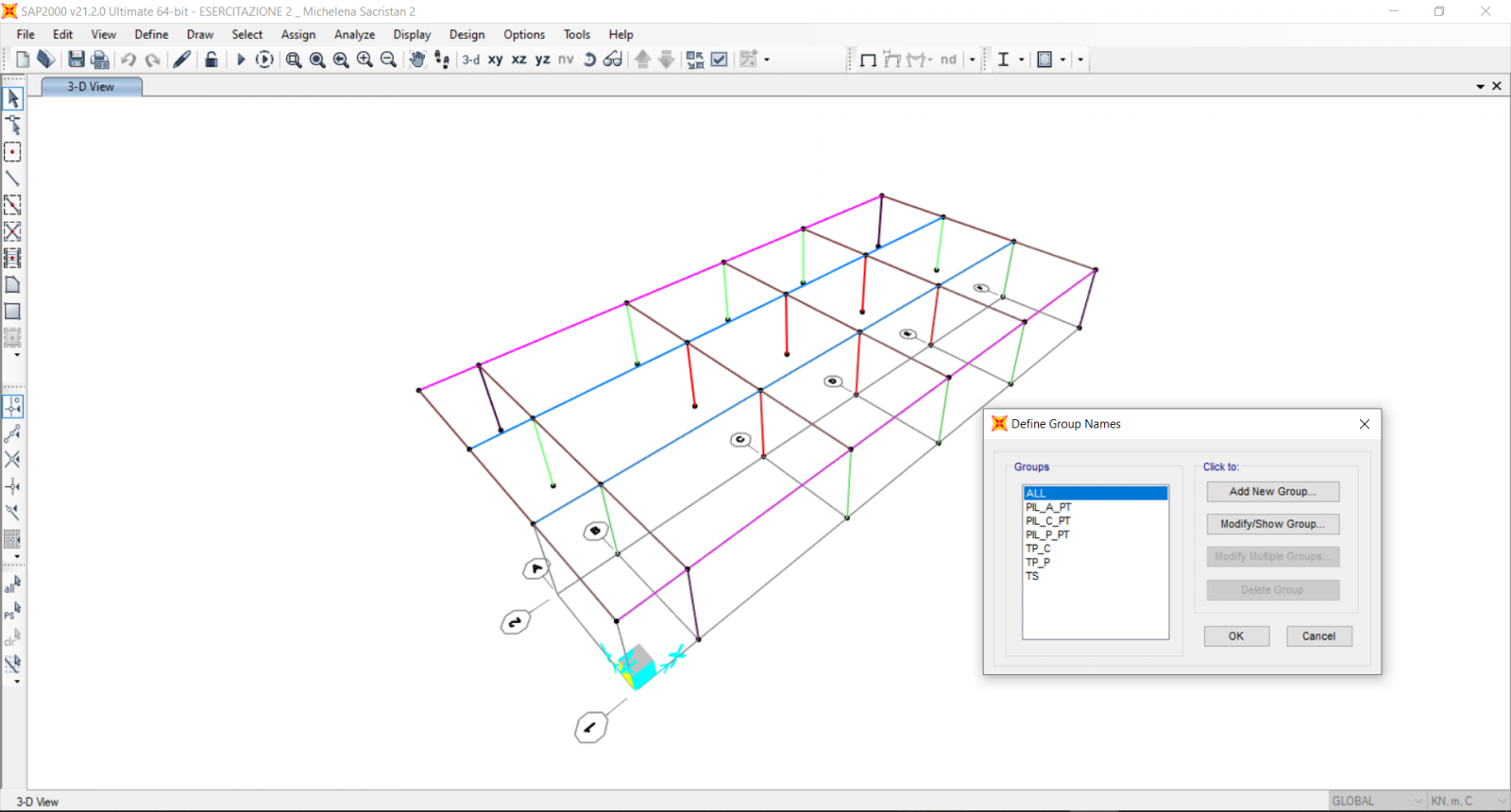
5 DEFINIZIONE GRUPPI DI ELEMENTI IN SAP :
Prima di poter procedere identifichiamo dei gruppi a cui assegneremo gli elementi in Sap, al fine di avere un modello ordinato e non fare confusione nei seguenti passaggi , fino alla lettura dei risultati delle tabelle che ci offre Sap.
Assign>Assign to group > new group :
- Travi principali centrali > TP_ C
- Travi principali perimetrali > TP_P
- Travi secondarie > TS
- Pilastri Centrali PT > PIL_C_PT
- Pilastri perimetrali PT > PIL_P_PT
- Pilastri angolari PT > PIL_A_PT
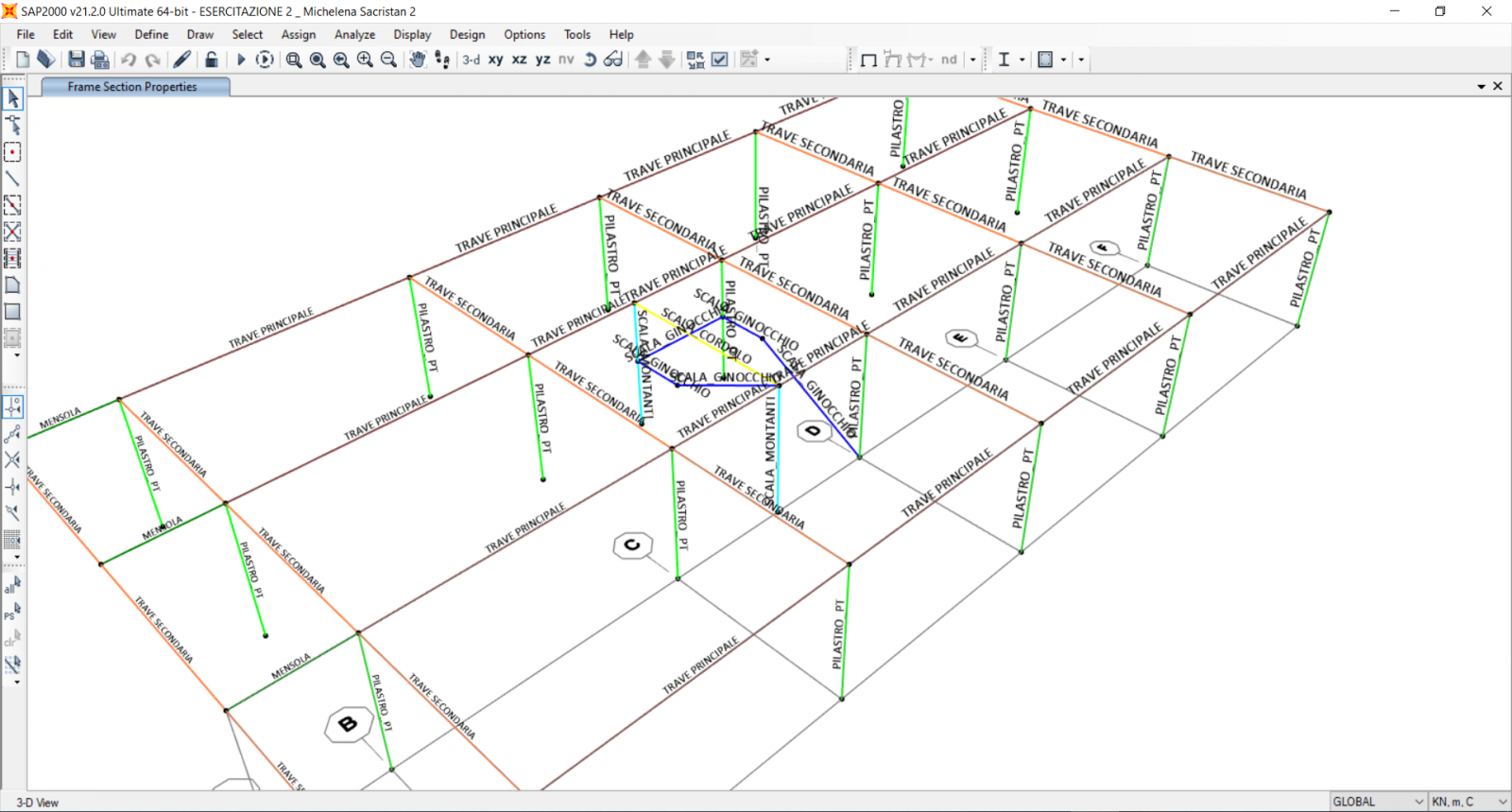
6 DEFINIZIONE GABBIA SCALE E TRAVE A GINOCCHIO :
Gabbia scale composta da una rapa simmetrica , larghezza totale 2,4 mt e pianerottolo 1,2 mt.
Define > Section Properties > Frame section
Definiamo quindi :
- SCALA _ CORDOLO = 30x 25 cm
- SCALA _ GINOCCHIO = 45 x 30 cm
- SCALA _ MONTANTI = 30 x 30 cm
Disegnamo su sap con lo strumento Draw Special Joints .
Dopo aver disegnato tutti gli elementi che compongono la gabbia scale raggruppiamo anche questi in un nuovo gruppo . Define > Groups> Gruppo Scale . Selezione degli elementi >Assign > Assign to group.
Assegnamo quindi le sezioni anche a questi elementi :
Per il corpo scala dovrò far considerare a Sap che gli elementi sono legati al resto della struttura. Per fare questo si procede con Edit > Edit lines> Divide Frames> Break intersection .
7 CREAZIONE DI ALTRI PIANI :
Per copiare degli oggetti con le proprietà assegnate utilizziamo il comando Ctrl + R / z = 3 (mt) / Increment Data = 2 paini .
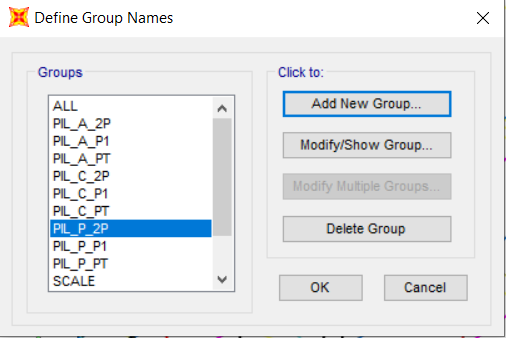
8 ASSEGNAZIONE ELEMENTI DI ALTRI PIANI A GRUPPI :
View>Set 3D view > xy>aperture = 0 > ok . Selezioniamo gli elementi che mi interessa aseegnare ad un determinato gruppo .
Definiamo Gruppi di pilastri per ogni piano :
- PIL_A_P1
- PIL_C_P1
- PIL_P_P1
- PIL_A_P2
- PIL_C_P2
- PIL_P_P2
Alla fine di questo processo di assegnazione abbiamo i seguenti gruppi di elementi :
- Travi principali
- Travi secondarie
- Scale
- 3 gruppi di pilastri per piano

9 ASSEGNAZIONE DEI VINCOLI
View>set 3d view > yz > aperture = 0 > selezione di tutti i punti alla base dell’edificio >assign >joints >restraints>incastro.
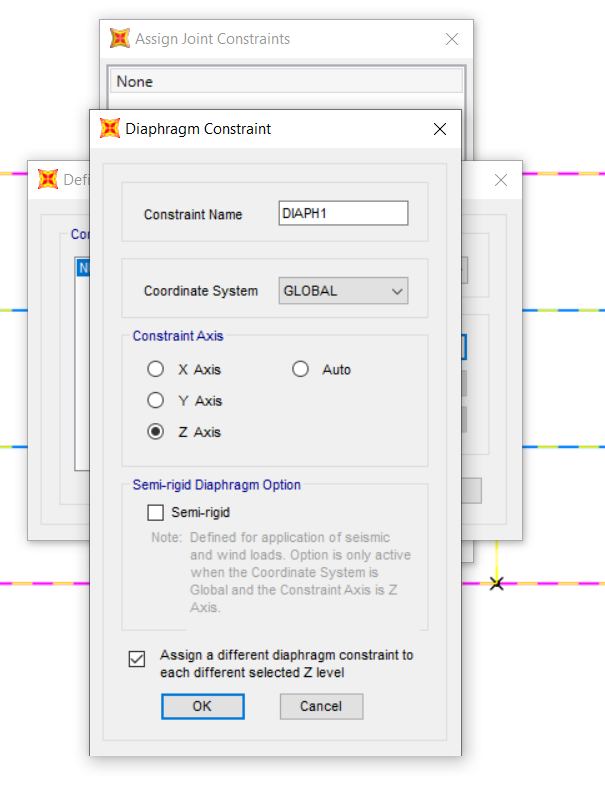
DIAPHRAM : view>set 2d view> xy > z = 3 , z= 6 , z = 9 > si assegnano a tutte le travi il Diaphram ( condizione di impalcato rigido ).
Assign > Joints> Costraints> Diaphram . Spunta a tutte le quote di impalcato .
10 ASSEGNAZIONE DEI CARICHI :
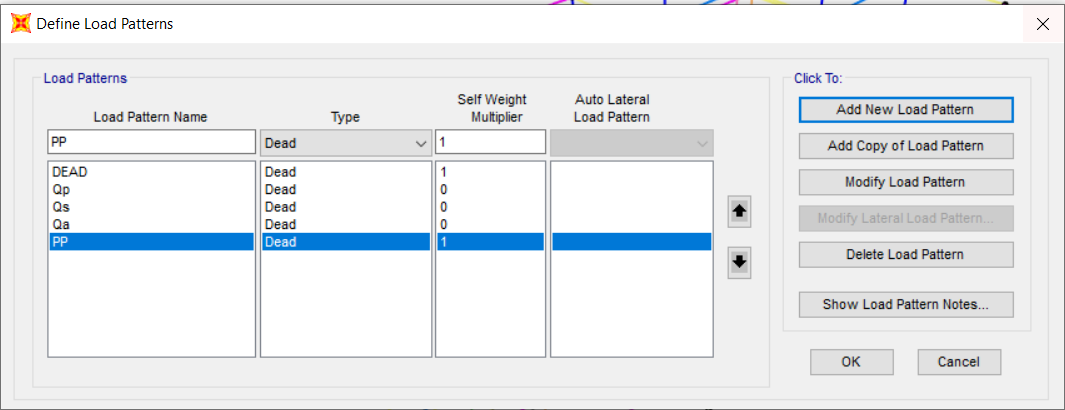
Definiamo in Sap dei Load Pattern che poi serviranno per determinare una combinazione dei carichi allo stato limite ultimo.
Define>Load Pattern>Qs , Qp , Qa , PP .
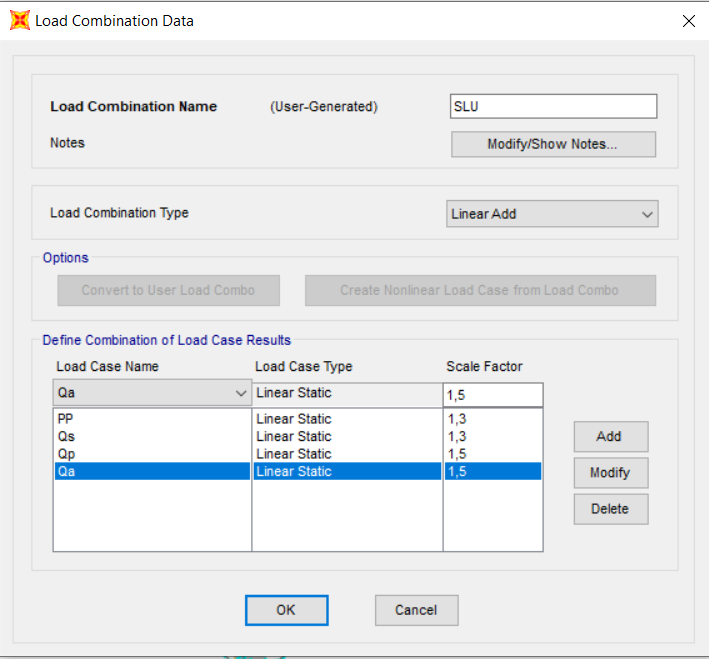
Define >Load Combination> Add new Combo > “SLU” >Linear Add.
Ricostruiamo così in Sap la formula della combinazione di carico allo stato limite ultimo inserendo i fattori ( coeff. Di sicurezza da normativa ).
uesta combinazione di carico verrà assegnata alle travi principali.
11 CALCOLO DEI CARICHI NELE TRAVI :
Travi Centrali principali : interasse 4 mt
- Qs = 4 x 3, 28 = 13,12 kN/mq
- Qp = 4 x 3,77 = 15,08 kN/mq
- Qa = 4 x 2 = 8 kN/mq
Travi Perimetrali Principali : interasse 2 mt
- Qs = 2 x 3,28 = 6,56 kN/mq
- Qp = 2 x 3,77 = 7,54 kN/mq
- Qa = 2 x 2 = 4 kN/mq
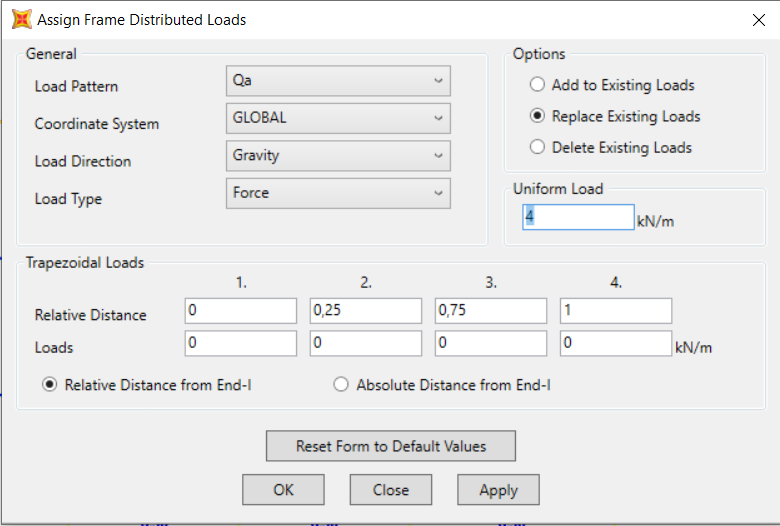
Assegnamo ora i carichi su Sap. Assign>Frame Loads> Distributed .
12 AZIONE DEL VENTO:
Prima di procedere con l’analisi in Sap è opportuno considerare in questa esercitazione una delle due grandi forze orizzontali agenti . In questo caso proviamo a inserire la forza orizzontale del VENTO .
Immaginiamo quindi che questa sia una forza agente sull’edificio e che eserciti una pressione sulle superfici in facciata.
Ogni pilastro riceverà quindi una parte del carico del vento in funzione della sua area di influenza.
Se stimiamo che il vento è pari a 0,5 kN/ mq , dobbiamo moltiplicarlo per l’interasse e otterremo quindi un carico distribuito al ml da assegnare ai pilastri .
allora :
- Pilastri angolari : 2 x 0,5 = 1 kN/ml
- Pilastri centrali : 4 x 0,5 = 2 kN/ml
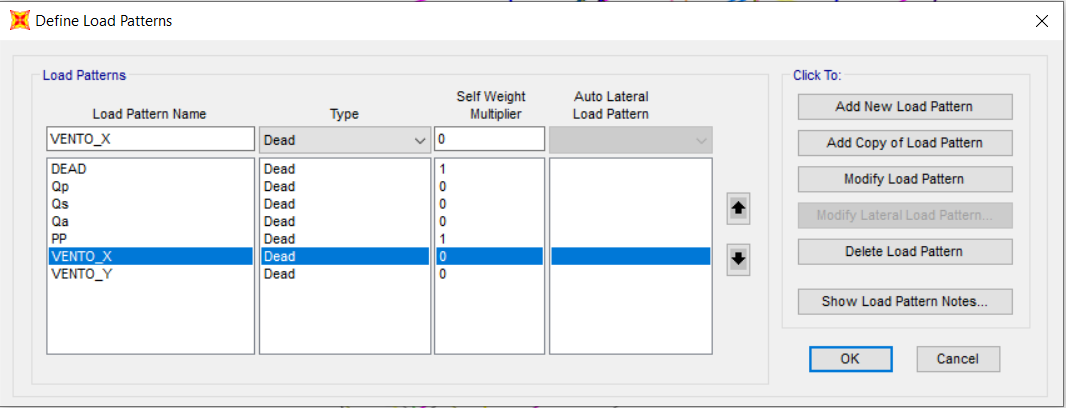
Creiamo in Sap un nuovo Load Pattern che chiameremo “Vento X e Vento Y” .
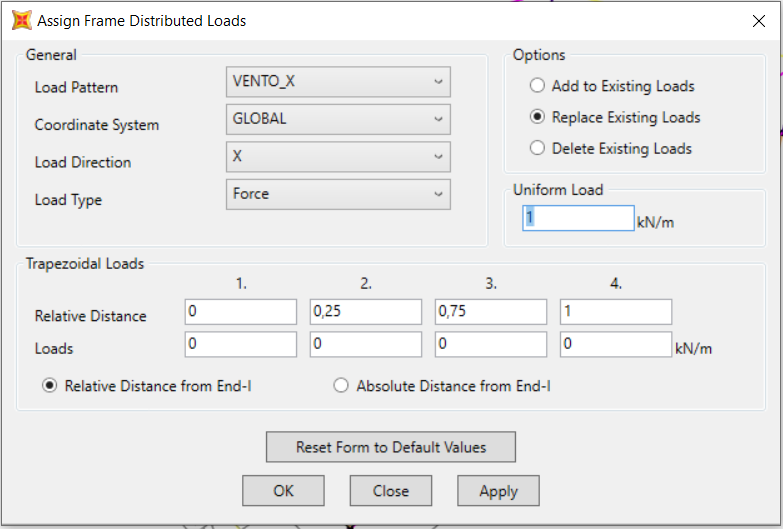
Successivamente lo assegniamo ai pilastri Frame >frame Loads >Distributed.
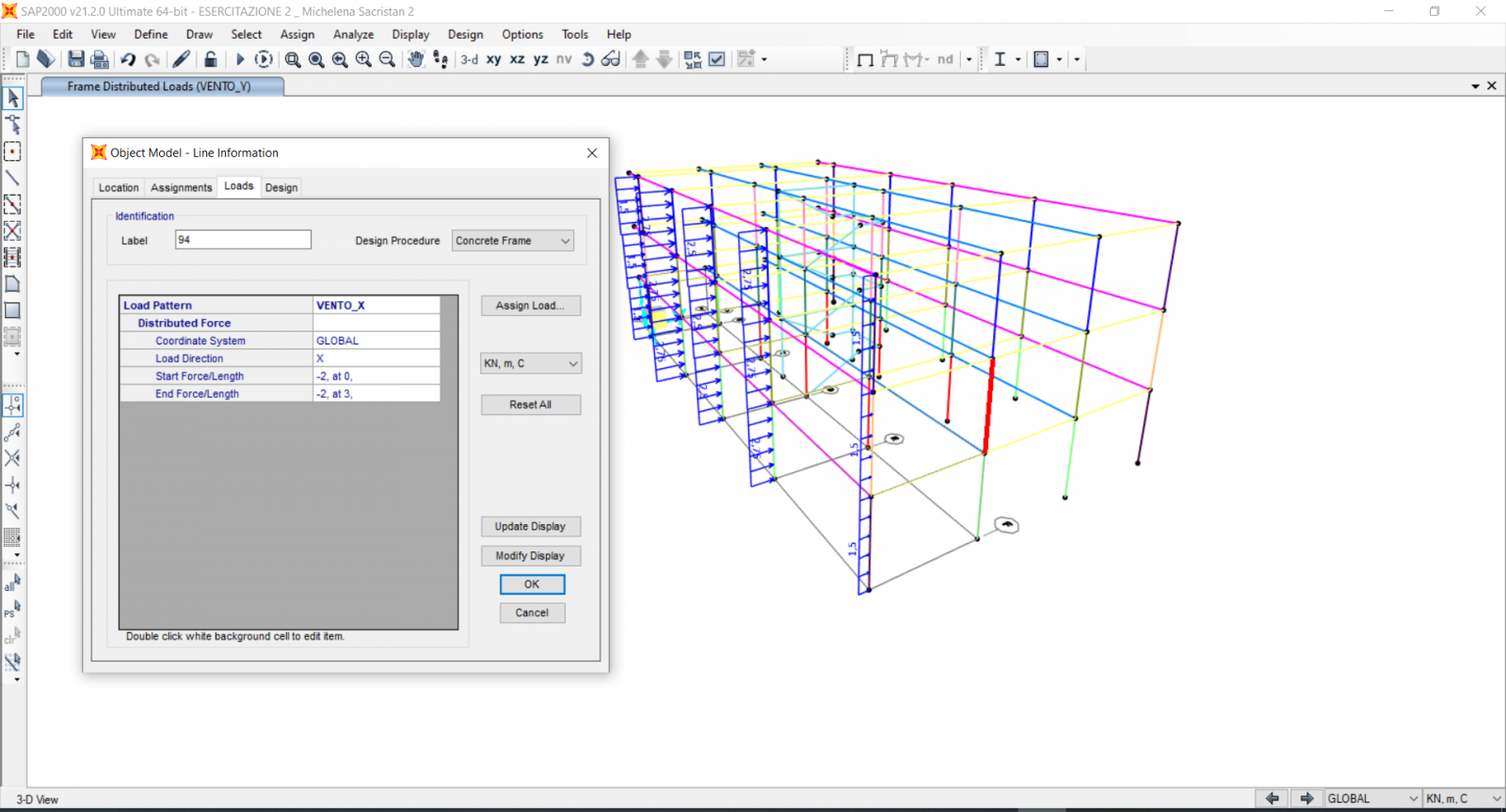
13 CREAZIONE COMBINAZIONI DI CARICO SLU + VENTO :
Prima di poter avviare l’analisi nella quale considereremo la combinazione allo S.L.U e l’azione del vento su ogni gruppo di elementi della nostra struttura , è opportuno creare altre due combinazioni di carico che ci aiutano a capire meglio il comportamento del nostro edificio in funzione della direzione x o y del vento.
Avremo quindi :
- COMB1_X = Vento x + SLU
- COMB1_Y = Vento y + SLU

14 ANALISI ED ESPORTAZIONE TABELLE XLS :
Possiamo ora avviare l’analisi per ogni combinazione di carico (incluse le sollecitazioni dovute al vento) e vedere i valori Max nelle travi e dimensionarle a flessione, stessa cosa faremo con i pilastri di ogni piano per dimensionarli a pressoflessione.

Esportazione delle tabelle xls : Esportiamo le tabelle aiutandoci con la distinzione dei gruppi creati su Sap per visualizzare al meglio i valori di sforzo normale e momento negli elementi strutturali.

Peri i Pilastri : Dovremo quindi comparare le tabelle per capire quale è la combinazione di carico più sfavorevole. (SLU + Vento x o SLU + Vento y ).
Nel nostro caso la combinazione di carico SLU + Vento in direzione Y sembra essere quella peggiore.
Leggeremo i risultati riportati nelle tabelle che ci serviranno per identificare i valori di sforzo normale e momento max flettente per capire in che caso di eccentricità di troviamo .
15 VERIFICA PILASTRI A PRESSOFLESSIONE:
Per capire il valore della e (eccentricità) , dovremo quindi prendere il momento max che si verifica nei pilastri (facendo distinzione per gruppi – angolari, perimetrali e centrali) e dividerlo per lo sforzo normale N.
Quindi M/N = e .
Nel nostro caso : riscontriamo che i pilastri di ogni piano risultano avere eccentricità diverse . Quindi per maggiore chiarezza riportiamo qui di seguito le tabelle che abbiamo prodotto con la distinzione dei pilastri per piano e la loro specifica eccentricità.
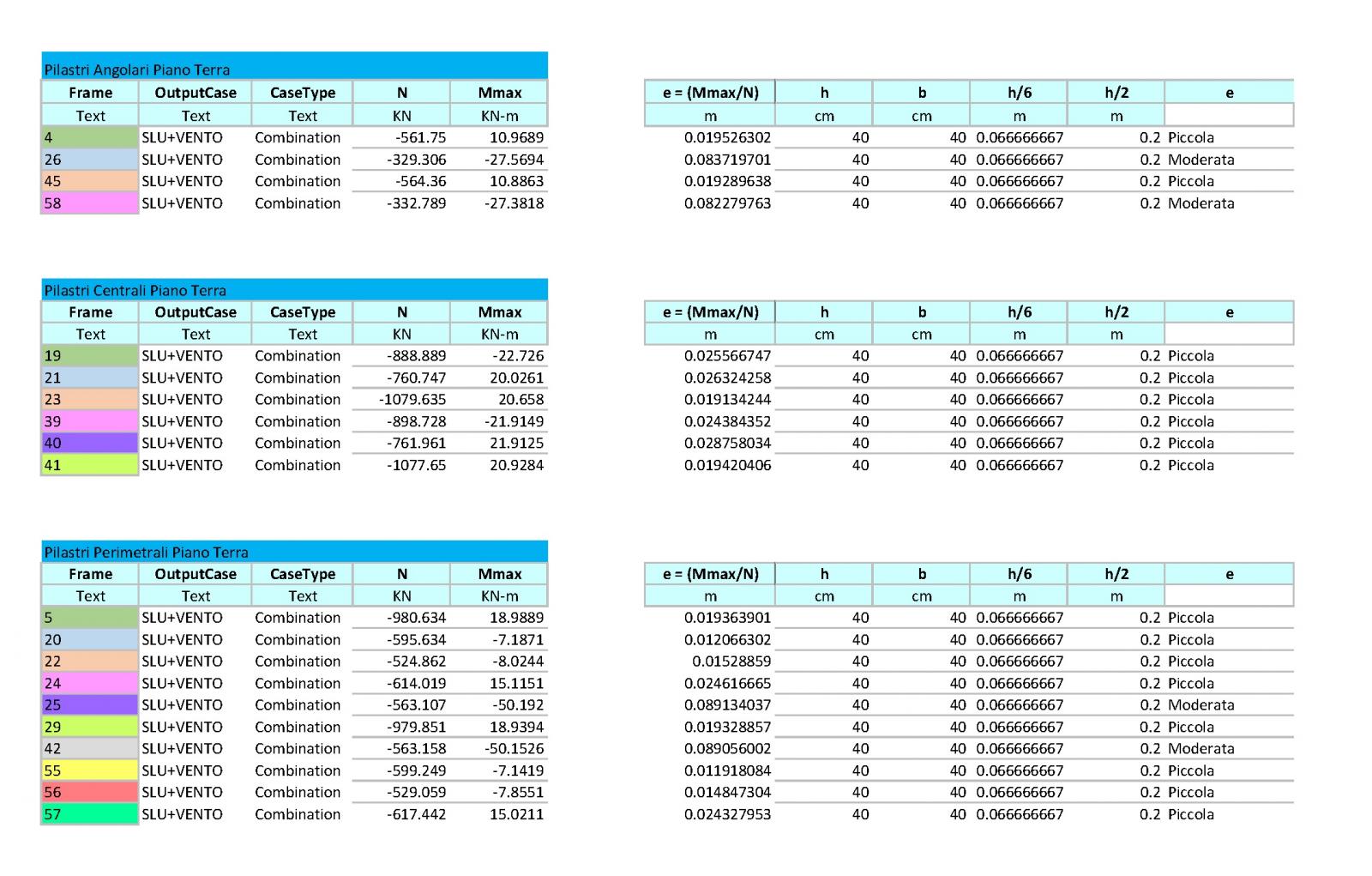
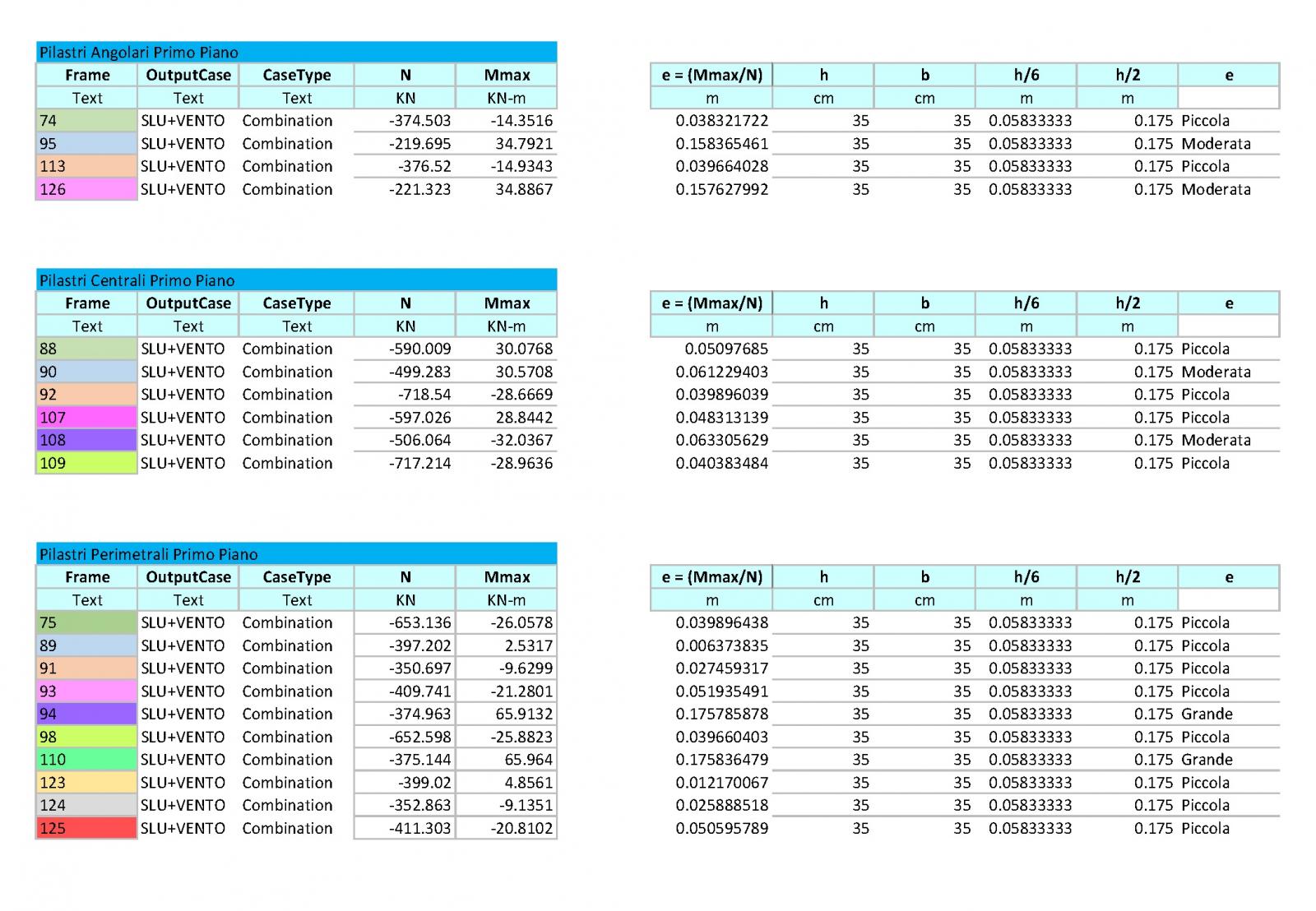
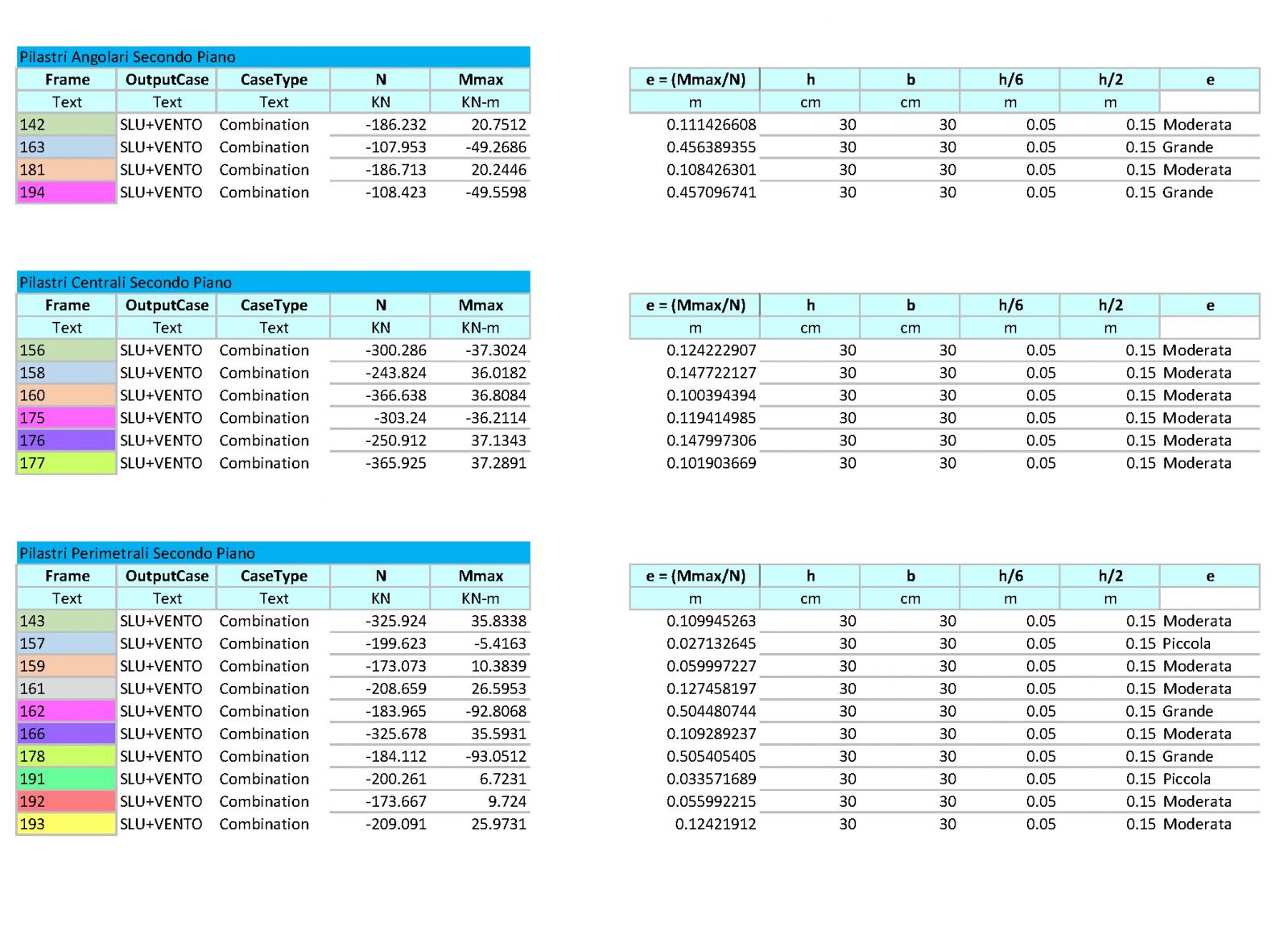
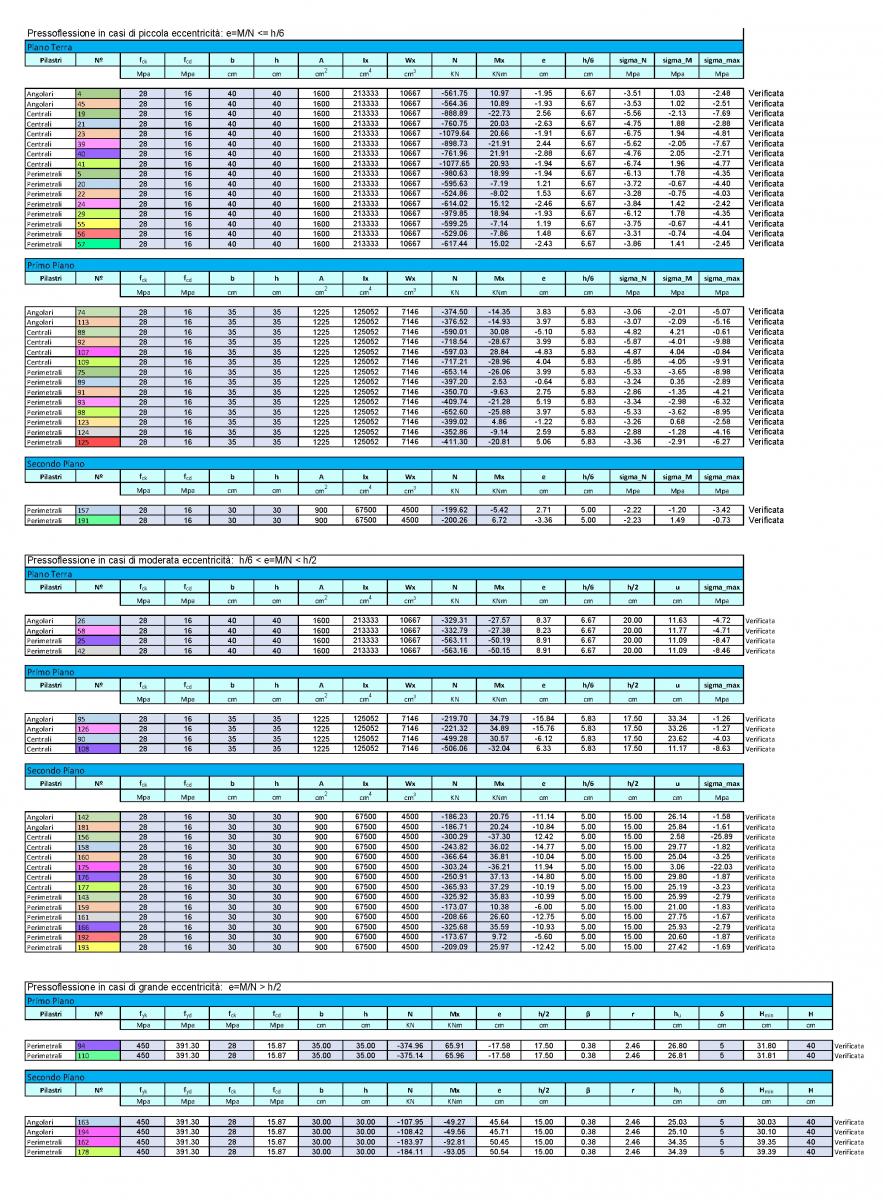
CONCLUSIONI VERIFICA PILASTRI : i pilastri del nostro edificio risultano essere tutti verificati.
16 VERIFICA TRAVI A FLESSIONE:
Dopo aver esportato da Sap le tabelle , divise per gruppi, per la verifica a flessione delle travi , siamo intervenute sulla sezione della trave principale centrale.
In realtà, risultava verificata semplicemente cambiando il valore di fck del cls , ma non ci sembrava adeguato in quanto nella realtà di cantiere sarebbe difficile gestire il cambiamento di un materiale solamente per così pochi elementi in un edificio di altezze contenute.
Siamo quindi giunte alla soluzione di aumentare la base della trave, affinchè sia verificata.
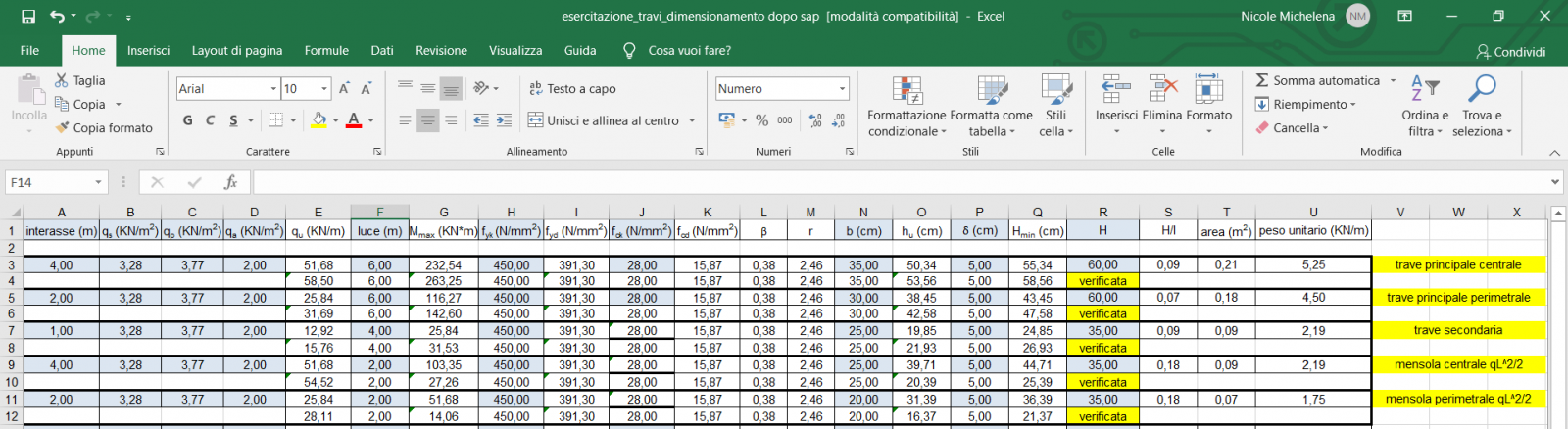
Nella tabella di verifica sotto riportata vi è anche la verifica delle mensole, cambiando il valore del Mmax in qL^2/2 , tenendo in considerazione un modello di mensola a sbalzo con incastro.
Commenti recenti