blog di Giovanni.Saja

Costruendo un impalcato con travi e pilastri in cls armato di tipo shear - type studiamo come reagisce sotto l'azione di una forza  sismica orizzontale, la struttura per resistere necessita di essere controventata. I controventi di un impalcato sono rappresentati proprio dai telai che assorbono la spinta e rispondono come una molla sottoposta a compressione.

F= K*∂

L'impalcato viene costruito con una trave di altezza h= 70cm e pilastri di sezione 30x30 cm. Viene scelto un cls con classe di resistenza 25/30 che avrà un modulo elastico E= 25000 N/mmq.

Per calcolare la rigidezza traslante di ogni telaio abbiamo bisogno del momento d'inerzia rispetto all'asse in cui agisce la forza sismica, nel nostro caso l'asse X.

I x = b* h³/12 =67500 cm⁴

Adesso calcoliamo la rigidezza per ogni telaio con la formula : 12 EIx/ h³

Riassunto delle rigidezze di ogni telaio 

Calcolo del centro di massa dell'impalcato.

Con un procedimento simile, moltiplicando la rigidezza di ogni telaio per la distanza dell'origine ( pilastro 11),

si calcola il centro di rigidezza.

Considerando un pacchetto di  solaio in cls armato già calcolato in un esercitazione precedente si analizzano i carichi sismici agenti sulla struttura considerando i coefficenti di contemporaneità ed intensità sismica.

Le tabelle seguenti riportano come la forza si distribuisce lungo le direzioni orizzontale e verticale nella pianta della struttura.

Adesso verifichiamo i calcoli applicandoli su un modello costruito con SAP.

Il modello rappresenta l'impalcato disegnato precedentemente , i pilastri vengono  fissati alla base con un vincolo incastro mentre per rendere le travi di tipo shear - type  aumentiamo con diversi zeri il momento d'inerzia di quest'ultime rispetto agli assi X e Y . Inoltre diciamo al programma con il comando Diaphragm di traslare allo stesso modo i nodi trave - pilastro.

Tramite il comando offset definiamo i rispettivi centri di rigidezza e massa.

Adesso assegnamo la forza F nel centro di massa e verifichiamo con l'analisi.

Il solaio trasla e ruota leggermente subendo una minima rotazione poichè il centro delle masse e quello delle rigidezze non coincidono, per diminuire ancora di più tale rotazione si può irrigidere i pilastri aumentandone la dimensione in sezione.

Considerato un telaio con uno sbalzo di luce pari a 3.00 m e interasse uguale calcolo il carico che agisce sulla trave più sollecitata verificando che la deformabilità della trave sia inferiore a 1/250 della sua luce. Si consideri  come carichi strutturali , permanenti e accidentali i valori dell'esercitazione precedente nelle tre diverse tecnologie.

SOLAIO IN LEGNO

Qs=0,2 KN/mq; Qp=2,07 KN/mq; Qa=3,00 KN/mq

Lo sbalzo è verificato per una trave di 35x 45 cm in sezione.

SOLAIO IN ACCIAIO

Qs= 2,24 KN/mq; Qp= 3,54KN/mq; Qa=3,00KN/mq

Dal calcolo emerge che, rispetto al modulo di resistenza a flessione, il momento d'inerzia e il peso della trave ipotizzata non è sufficente a reggere lo sbalzo. Si procede allora considerando in tabella il valore immediatamente superiore sostituendo il momento d'inerzia e il peso della trave.

Lo sbalzo è verificato con una trave IPE 360.

SOLAIO IN CLS ARMATO.

Qs=1,50KN/mq; Qp=2,63KN/mq; Qa=6,00KN/mq

Dal calcolo inserendo la resistenza delle armature e la classe di resistenza del calcestruzzo emerge che lo sbalzo è verificato per una trave di 30x40 cm in sezione.

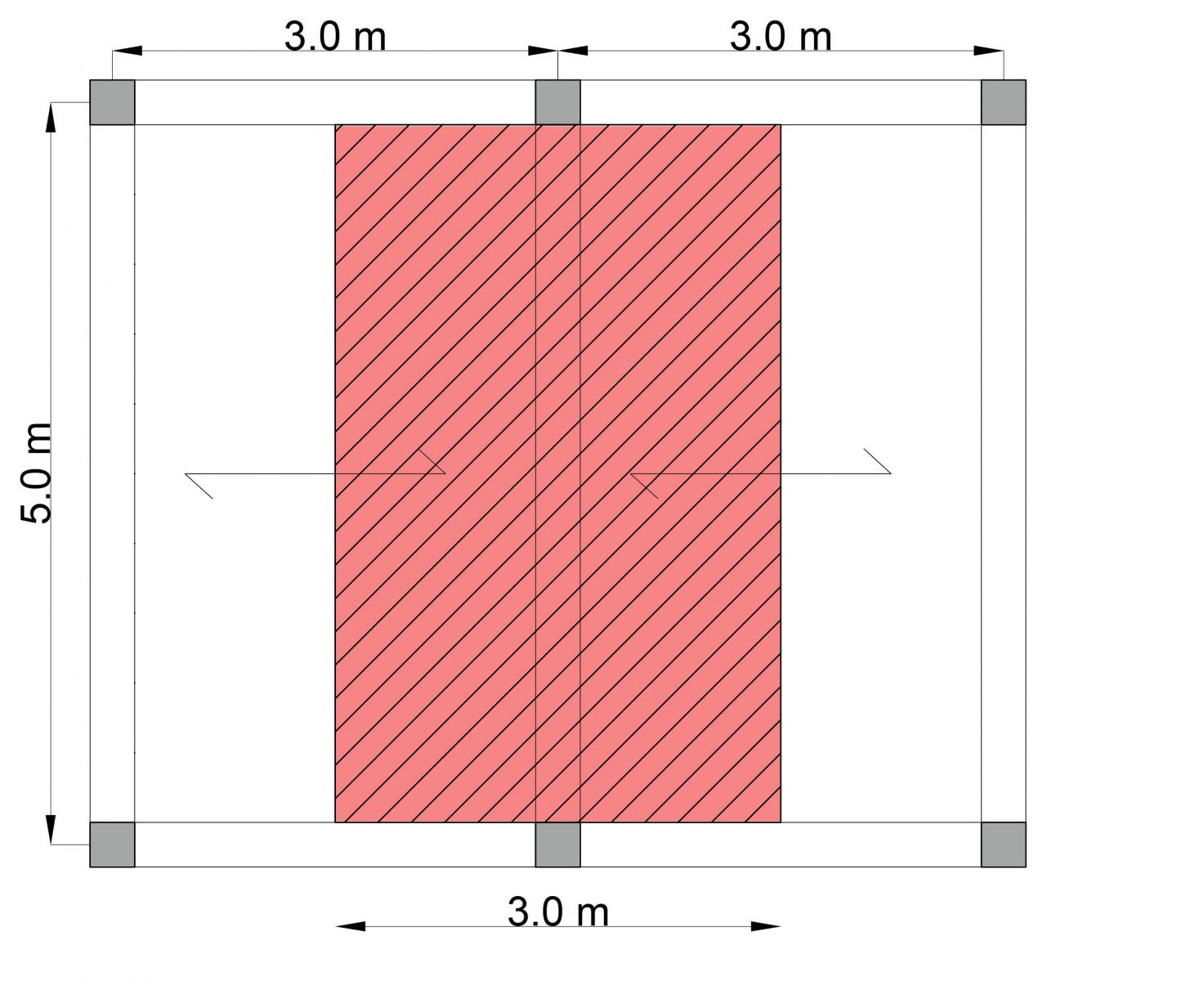
Basandomi su questo telaio vado a dimensionare la trave più sollecitata considerando tre diverse tecnologie.

SOLAIO IN LEGNO

Q= qs + qp + qa

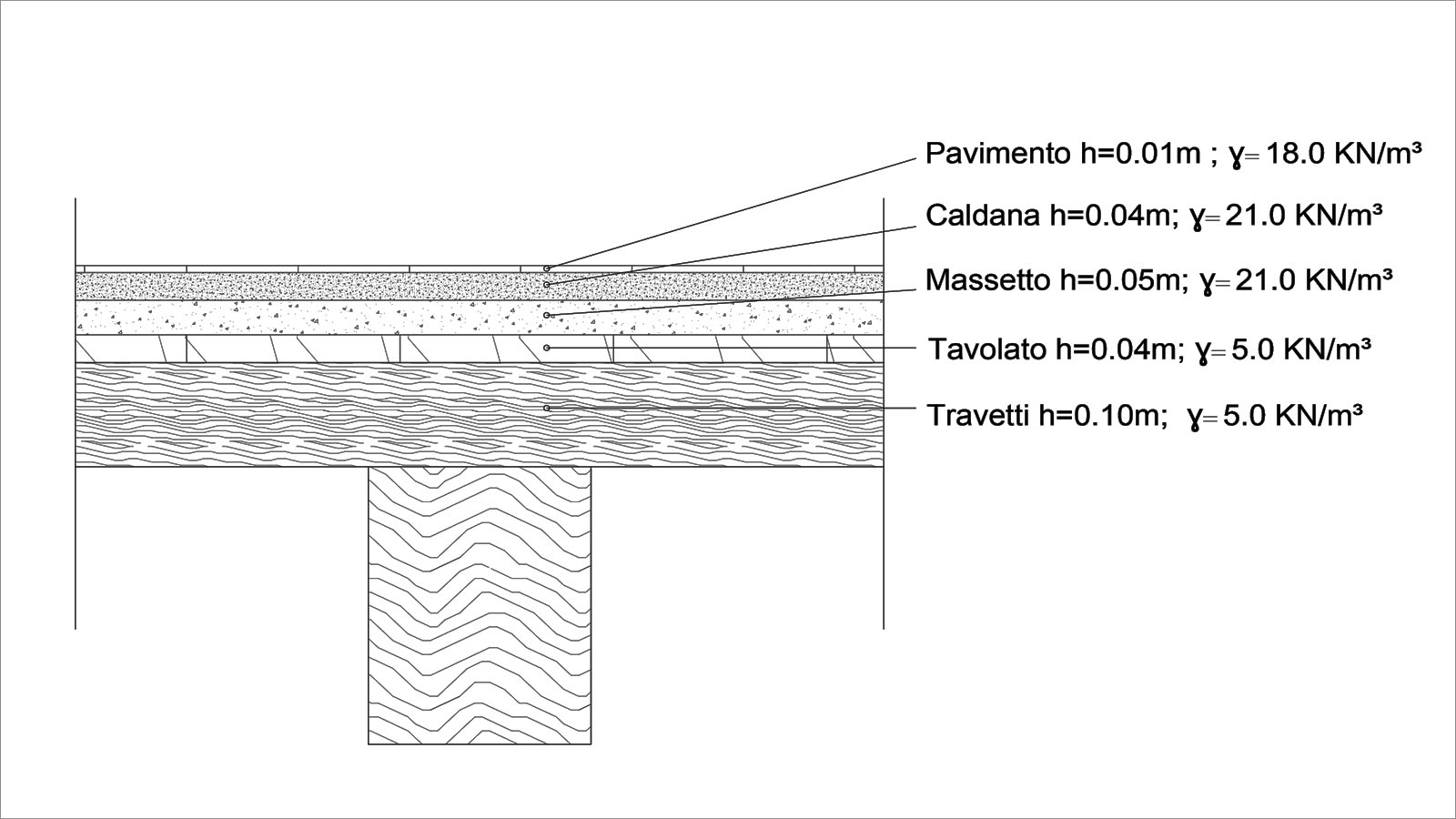
qs: Travetti e tavolato in pioppo.

qp: Massetto e caldana di sottofondo in malta di cemento, pavimentazione in laterizio.

qa: Uffici aperti al pubblico.

qs= 0.04m x 5.0 KN/mc = 0.2 KN/mq

qp=0.09m x 21 KN/mc + 0.01m x 18.0 KN/mc = (1.89 + 0.18) KN/mq = 2.07 KN/mq

qa= 3.0 KN/mq

Per il dimensionamento dei travetti considero un interasse di 50 cm ed una luce di 3m.

Dal calcolo mi risulta h= 13.8 cm, scelgo quindi dei travetti con sezione (10x15)cm  in pioppo.

Aggiungo a qs il carico dei travetti per dimensionare la trave.

qs=[( 0.1 x 0.15)m x 5.0 KN/mc] 2+ 0.2 KN/mq = 0.35 KN/mq

Per il dimensionamento della trave considero un interasse di 3m ed una luce di 5m.

Ipotizzando una base di 30cm ottengo un altezza di 32.9 cm, scelgo per sicurezza una trave di 30x40 cm.

SOLAIO IN CLS ARMATO

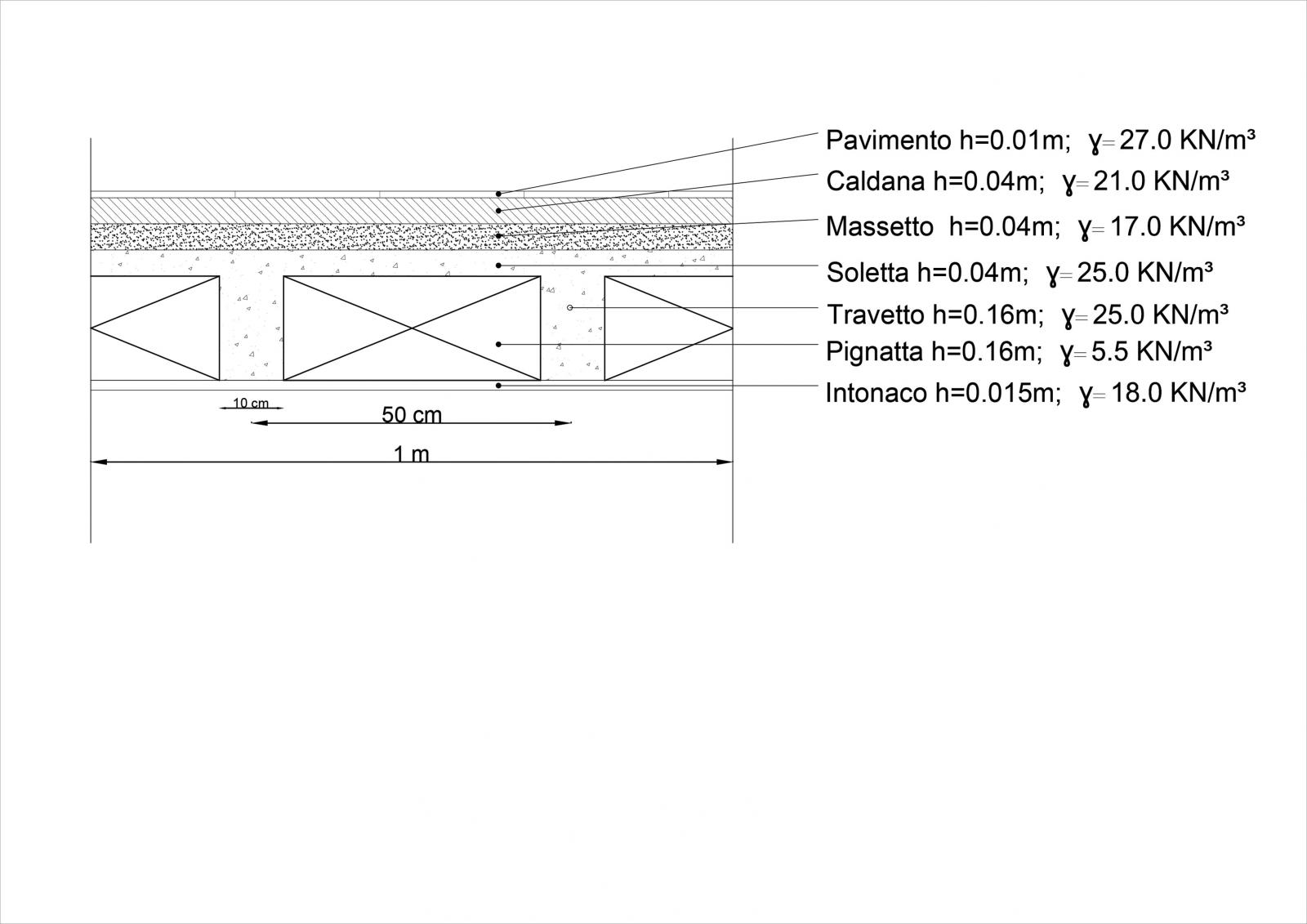
qs: Pignatte in Laterizio, Travetti in cls armato.

qp: Massetto in sabbia, caldana di sottofondo in malta di cemento, pavimentazione in granito, tramezzi e impianti

qa: Biblioteca.

qs= [(0.10 x 0.16)m x 25 KN/mc] 2 + [(0.16 x 0.4) x 5.5 KN/mc] 2= 0.8 +0.7=1.5 KN/mq

qp= [(0.06m x 17KN/mc ) + (0.04m x 21KN/mc) + (0.01m x 27KN/mc)]= 1.02+0.84+0.27= 2.13 + 1.5=3.63KN/mq

qa= 6 KN/mq

Inserisco i dati in tabella scegliendo  l'acciaio dell'armatura  B450C e un calcestruzzo con elevato rapporto resistenza cilindrica / resistenza cubica, ad esempio C45/55.

Dal calcolo ipotizzando b= 25 cm ottengo h= 27.8 cm quindi mi metto in sicurezza scegliendo una trave di 25 x 30 cm.

SOLAIO IN ACCIAIO

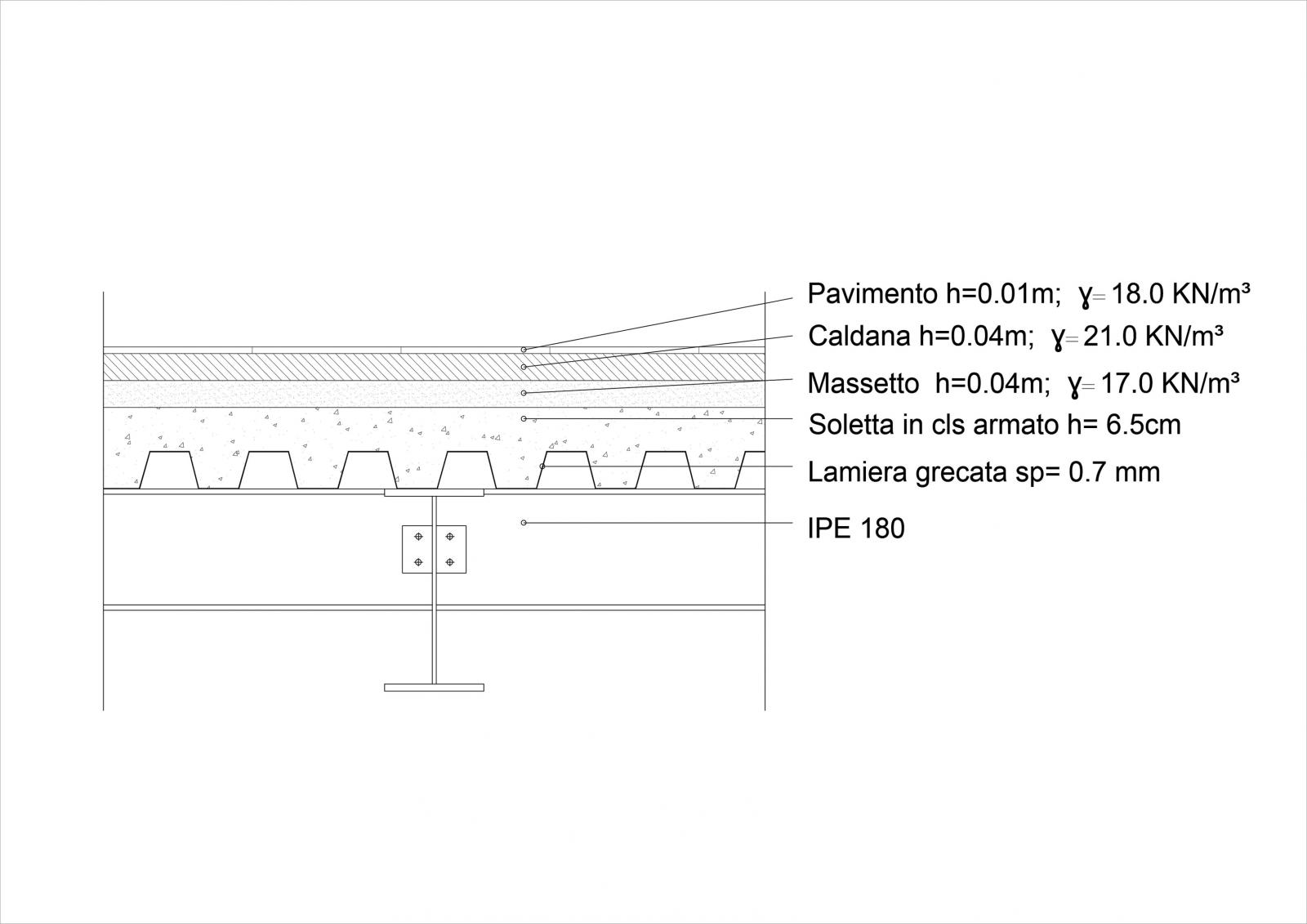
qs= Massetto in cls armato con rete elettrosaldata di sp= 8mm agganciata alla lamiera grecata hi- bond sp=0.7mm.         sostenuta da una trave secondaria IPE 180.

qp=Pavimento in laterizio, caldana di sottofondo in malta di cemento , massetto in sabbia, tramezzi e impianti.

qa= Uffici aperti al pubblico.

qs= [ (0.065m x 25KN/mc) + 0.06 KN/mq + 0.56KN/mq] = 2.24 KN/mq

qp= [( 0.01m x 18KN/mc)+ (0.04m x 21KN/mc) + (0.06m x 17KN/mc)]+ 1.5KN/mq = 3.54 KN/mq

qa= 3 KN/mq

Inserisco i dati in tabella scegliendo un acciaio F360/S235.

Dai risultati ottengo un modulo di resistenza Wx pari a 551.17 , quindi scelgo di utilizzare una trave principale IPE 300.

Il riferimento per l'esercitazione sulla trave reticolare è stato la pensilina d'ingresso alla Stazione Centrale di Roma Termini.

Usando Rhinoceros  con una spline ho copiato da un bitmap di sfondo impostato sulla vista frontale la curva della pensilina, successivamente ho impostato i frame della struttura con lunghezza di 1.5 mt  in un modulo di 20x20.Il risultato è stato una piastra reticolare ondulata.

Importando da Rhino su Sap ho dovuto prima esplodere tutte le polilinee del file Rhino, ho evitato di lavorare sul layer di default e infine salvato il modello in formato Iges. Dato il comando di import ( file-import-iges file ) ho trasferito il file su Sap.

Dopo aver importato la struttura su SAP ho imposto da Edit ( edit- edit points- merge) tolerance 0.1 e dato ok. Essendo una trave reticolare non abbiamo momenti nei nodi perciò ho impostato i momenti 3-3, i momenti 2-2, e la torsione iniziale pari a 0.

Definite le condizioni iniziali di equilibrio ho specificato la tipologia di trave da Assign ( assign- frame- frame sections ), in questo caso un tubolare ( Pipe ) in acciaio ( Steel ).

Il passo successivo è stato definire il carico che dovrà incidere sulla struttura. Partendo da Assign ( assign- joint loads- forces ) ho impostato una forza F e che esclude il peso della struttura .

Definito il materiale della struttura, la tipologia degli elementi che la compongono, i vincoli ed il carico agente su essa ho dato comando al programma di effetture l'analisi delle sollecitazioni (Analyze- Run analyze- Run Now, selezionando il carico F).

L'analisi ha prodotto la deformata della struttura ed i diagramma degli sforzi normali. In questo modo è stato possibile chiedere a Sap di mettere in tabella i risultati dell'analisi dal comando Display.( Display- Show Tables- Analysis Results- Select Load Patterns- Ok ).

Creata la tabella ho selezionato i risultati che mi interessava conoscere, Element Forces- Frames.

Visualizzati i risultati ho esportato la tabella che mi interessava su un file Excel dal menù a tendina File. (File- Export Current Table- to Excel ).

Sulla tabella del file Excel ho ordinato i valori degli sforzi normali P dal più grande al più piccolo individuando l'elemento della struttura  con il valore più alto. L'asta numero 899 della struttura, situata in corrispondenza della cerniera è risultata la più sollecitata.