blog di fedefede

Analisi di tre tipologie di struttura ad arco.

 

Abbiamo analizzato diverse tipologie di strutture ad arco, dove sono stati creati e messi a confronto tre sistemi strutturali vincolati in egual modo, dove l’unico elemento che cambiava era la forma.

Uno è l’arco parabolico, uno l’arco a tutto sesto e arco ribassato.

Gli archi sono tutti definibili come archi a tre cerniere. L’unico elemento quindi, che li contraddistingue , e dunque li fa lavorare diversamente, è la loro forma.

Essendo tutti archi, tutti e tre rispondono ai carichi verticali per compressione più che per flessione.

Lavorano quindi come strutture spingenti, esercitando cioè la cosiddetta forza di spinta nella sezione in chiave.

La forza di spinta è data da una formula parametrizzata, pari a:

H= ql^2/2f 

Da cui si capisce bene che i parametri da cui dipende la forza di spinta sono la luce l e la freccia f.

La formula spiega come, da una relazione di luce e freccia dell’arco è possibile ricavare la forza centrale che fa perno sulla sommità dell’arco , la quale, in assenza di vincoli rischia di provocare dunque una possibile perdita di forma e dunque una deformata.

Ma ciò non accade, perché la controspinta delle cerniere all’imposta dell’arco esercita una forza uguale e contraria a quella in sommità, impedendole di sbilanciare la struttura.

 

 

 

 

Per svolgere l’esercitazione su SAP, sono stati seguiti degli step.

Innanzitutto il disegno dell’arco realizzato su autocad , uno per ogni tipo di arco, tutti spezzati in chiave.

Essi sono stati successivamente riportati in SAP , dove sono seguite le seguenti fasi in tutti e tre i casi:

 

-Rilascio dei momenti nel punto centrale interno all’arco

( assign --> frame --> release partial fixity --> spunta sulla casella m3-3 peima start , poi end , in due riprese differenti, questo dopo aver selezionato i due segmenti ai lati del punto di chiave in sommità uno per volta)

 

-Impostazione dei vincoli cerniere all’imposta dell’arco ( seleziono punti di imposta -->assign -->joint -->restraints-->selezione del vincolo cerniera.)

 

-Assegnazione del materiale e delle caratteristiche di sezione

( Seleziono la struttura per intero --> assign --> frame --> frame section --> add new -->scelta del materiale concrete --> assegnazione base e altezza)

 

-Assegnazione del carico uniformemente distribuito di valore q=10KN/m (selezione completa dello schema strutturale-->assign --> frame loads--> distributed --> add new  (carico self multiplier =0) , selezionare la spunta dal menù a tendina gravity pojected  - assegnazione del valore nella stringa “load”)

 

-Avvio dell’analisi ( Run Analysis)

 

-Visualizzazione dei valori di sforzo assiale , taglio, momento flettente (show forces, frame)

-Verifica dei valori delle reazioni vincolari in cerniera

 

Di seguito gli screenshot delle varie fasi descritte in precedenza, affrontate per ogni tipo di arco :

Arco a tutto sesto :

 

l= f = r = 1 m

q=10 KN/m

H=ql^2/2f = (10 KN/m*1m)^2/2f  =50 KN

ql ( reazione vincolare verticale cerniera all’imposta ) = 10 kN/m *1,00 m =10kN

Rilascio momenti

 

Impostazione cerniere

Impostazione sezione

Forza uniformemente distribuita

Configurazione deformata 

 

Grafici sforzi assiali 

 

Arco ribassato :

 

l = 3 m

f = 2 m

q=10 KN/m

H=ql^2/2f = (10 KN/m*1m)^2/2f  =50 KN

ql ( reazione vincolare verticale cerniera all’imposta ) = 10 kN/m *1,00 m =10kN

 

Immagine 3d arco ribassato

Arco ribassato applicazione carico uniformemente distribuito 

 

 

 

Arco ribassato con carico distribuito agente 

 

Arco ribassato deformata 

 

 

Arco ribassato grafici sforzo assiale

 

Arco ribassato grafici momento

 

Arco parabolico :

 

l = 2 m

f = 3 m

q=10 KN/m

H=ql^2/2f = (10 KN/m*3m)^2/2*3  = 150 KN

ql ( reazione vincolare verticale cerniera all’imposta ) = 10 kN/m *1,00 m =10kN

 

 

Arco parabolico sezione applicata 

 

 

 

 

 

 

Arco parabolico carico uniformemente distribuito applicato

 

 

 

Arco parabolico deformata

 

 

Arco parabolico grafici sforzo assiale 

Consideriamo un impalcato di un piano tipologia shear type.

Siano affiancati all’impalcato dei controventi, i quali sono considerati vincoli cedevoli, rappresentati come molle. Questi ultimi intervengono a favorire la resistenza della struttura , quando forze orizzontali, come sisma e vento agiscono su di essa. Studiamo quindi come la struttura reagisce alle forze, supportata anche dall’azione dei controventi.

 

Siano:

Kv= rigidezza traslante dei controvento verticale

Ko=rigidezza traslante del controvento orizzontale

dv=distanza orizzontale del controvento dal punto O, origine degli assi

do=distanza verticale del controvento dal punto O

STEP 1: Calcolo rigidezze traslanti nell’edificio

Nel file exel, prendendo in esame ogni singolo controvento , e individuando gruppi di essi secondo l’allineamento del telaio orizzontale e verticale, possiamo conoscere la rigidezza di ognuno di essi K_T.

Dato E=21000 N/mmq e h = 5 m .

KT (KN/m) =12EItot/h^3  

Calcolo la rigidezza per gruppi di elementi strutturali, ossia per gruppi di pilastri che compongono il telaio.

Siccome ogni telaio raggruppa almeno tre pilastri, (o comunque più di due) il calcolo della rigidezza del telaio terrà conto di questo fatto. Infatti la rigidezza del telaio, a partire dal primo telaio orizzontale, sarà data dal modulo di elasticità, moltiplicato per la somma delle inerzie dei pilastri che ne fanno parte, per 12 il tutto diviso l’altezza, ossia la distanza su cui la forza applicata agisce.

Applicheremo questo metodo per i seguenti telai orizzontali e lo stesso faremo per i telai verticali. 

 

Step 2 Tabella controventi e distanze

La tabella seguente è una tabella riassuntiva delle rigidezze traslanti precedentemente trovate e delle rispettive distanze orizzontali e verticali rispetto un centro di riferimento dato un sistema di assi cartesiani in cui la struttura è inserita. Da cui 0 è il punto di origine da cui si calcolano le distanze. 

 

 

Step 3 Calcolo centro masse

Calcoliamo ora il centro delle masse.

Per semplificare il calcolo, abbiamo suddiviso la superficie in aree semplici , ossia in aree di rettangoli.

Questo servirà per poter calcolare di ognuna di queste aree il centro di massa, e di conseguenza partire da tre punti, tanti quanti il numero di aree scelte, per trovare il centro delle masse tra questi.

Il centro delle masse è quindi dato dalle due coordinate X e Y. Troviamo X , distanza del centro G (chiamo così il centro delle masse) dall’origine. Il suo valore sarà dato dalla somma del prodotto di ogni area con la sua rispettiva distanza dall’origine, il tutto diviso per la somma delle aree.

Usiamo lo stesso procedimento per trovare la distanza di tutto l’impalcato dall’origine a G, muovendoci sull’asse Y.

Step 4: Calcolo delle rigidezze globali e del centro delle rigidezze

 

Ora che conosciamo le rigidezze dei telai , possiamo procedere con lo studio.

Calcoliamo ora la rigidezza globale della struttura e di seguito il centro delle rigidezze assoluto.

La rigidezza globale è pari alla somma delle rigidezze del telaio che sto considerando.  

Adesso , il centro delle rigidezze, che mi consente di conoscere il punto di applicazione della forza orizzontale di natura sismica ( o atmosferica come il vento) , dunque molto importante, sarà il valore da cui parto per svolgere l’esercizio nella prova simulata.

Esso è dato da due coordinate X e Y calcolate rispetto all’origine . Il centro avrà nome C. Per la prima coordinata X, tengo conto dei telai verticali e delle loro distanze dall’origine; la seconda coordinata Y , tiene a sua volta conto dei telai orizzontali e la loro distanza dall’origine.

Le due coordinate si trovano con un rapporto , pari alla somma dei prodotti della distanza del singolo telaio dall’origine, moltiplicato per la sua rigidezza, il tutto diviso per la rigidezza totale sull’asse corrispondente, come prima specificato.

 

Step 5: Analisi dei carichi sismici  

 

Tale tabella è riassuntiva dei carichi che sono applicati sulla struttura, con i corrispettivi coefficienti di contemporaneità.

Tali coefficienti , servono per considerare l’improbabilità che le azioni agiscano simultaneamente.

E un calcolo del risultato complessivo della forza agente, di natura sismica o atmosferica che muoverà la struttura nel senso orizzontale.

Step 6/7 ripartizione della forza sismica su X eY:

 

La forza risultante sarà ripartita sui due assi X e Y , specificando con i valori della tabella , come cambia l’intensità di volta in volta e su quale telaio.

Le tabelle indicano anche , a seconda del punto di applicazione della forza, valori di angoli e spostamenti.

Siccome il tipo di spostamento della struttura dipende strettamente dal punto in cui è applicata la forza, l’angolo è quell’angolo che si crea tra il punto iniziale e quello della deformata quando avviene rotazione, mentre lo spostamento si ha laddove la forza è applicata nel punto che genera solo traslazione. 

Vediamo ora cosa accade riportando la struttura in SAP

Con i passi e gli svolgimenti indicati sopra abbiamo inserito e ricavato valori dalla tabella.

Ho disegnato la struttura della tabella in SAP e mi sono servita dei valori calcolati per applicare la forza e vedere cosa succede.

Ho disegnato la struttura su una griglia tridimensionale su SAP , per ricostruire la situazione che avevo in alto nella tabella , dove il numero di pilastri e di telai e le loro reciproche distanze era specificato. 

 

Scegliamo e applichiamo i vincoli, il materiale e la sezione. 

Dunque passando alla pratica, selezioni tutti i punti ai piedi della struttura e inserisco gli incastri : bisogna cliccare su :

assign>joint>Incastro.

 

Quindi clicchiamo su ogni elemento strutturale e affidiamogli una sezione per materiale e dimensioni:

Assign> Frame > Frame sections> Add new property

Scegliamo concrete per la prima , e per tutti gli elementi strutturali. Differenzieremo però le travi dai pilastri dando ai pilastri una sezione 0,30 mx 0,30 m e alle travi una sezione di 0,70 m x 0,30 m, dove l’altezza è più marcata, per avere una rigidezza molto alta.   

Scegliamo di applicare la forza sul centro delle rigidezze, e verifichiamo cosa accade.

Cosa ci aspettiamo ?

Che data una forza orizzontale, applicata lungo Y , sul punto del centro delle rigidezze, la struttura non ruoti , ma trasli solamente.

Ora ci occupiamo di rendere infinitamente rigida la struttura , applicando diaphragm ai nodi, in modo che tutta la struttura si muova insieme.

Selezioniamo dunque tutti i punti sulla sommità della struttura, compreso il centro della rigidezza e applichiamo Assign> Joints> Constraints> nel menù a tendina a destra in alto : diaphragm>ok.

 

Adesso è il momento di verificare il nostro obiettivo.

Applicata la forza , per la quale dobbiamo cliccare su Assign>Joint loads>Forces>Load Pattern Name ( Creiamo una nuova forza ) >Applichiamo la forza su Y , per la direzione dovuta alla sua natura sismica.

 

Applichiamo l’analisi con >Run.

La struttura , per verificare la prova, dovrà traslare. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Possiamo fare lo stesso , solo applicando la forza sul centro delle masse.

Cosa ci aspettiamo adesso?

Che a struttura non trasli solamente , ma ruoti anche.

 

 

Il punto deve cadere dunque su centro delle masse, e sarà la prima cosa che disegneremo, al posto di quello precedente.

Le procedure da seguire sono le stesse eseguite per il caso precedente.

Dopo aver unito i punti insieme al centro delle masse, dovremo applicare la forza.

Essa sarà applicata su Y come prima. 

 

 

Se tutto va bene, vedremo adesso cosa succederà , e sarà diverso dalla situazione precedente.

Infatti , adesso dovrà verificarsi che la struttura, non trasla solamente ma ruota anche , intorno al punto di applicazione della forza.  La rotazione , per inciso, la sappiamo, dalle tabelle.

Dobbiamo dunque inserire la forza su SAP, avviare l’analisi, e verificare che questo avvenga.   

 

 

 

Legno

Prendo in considerazione gli stessi carichi dell’esercitazione precedente, ed eseguo l’analisi dei carichi per la mensola , cercando di inserire quei valori che permettono di ottenere  l/v > 250

 

Calcestruzzo armato

Considerando uno sbalzo di 4 m, riesco ad ottenere un giusto rapporto tra l e v , pari a 539,93, che tiene di gran lunga in sicurezza la struttura.

Il modulo di resistenza è pari a 448,53 cm^3.

La sezione che sceglierò in base al modulo di resistenza, sarà una IPE 300.

 

Acciaio

Considerando uno sbalzo di 4 m, riesco ad ottenere un giusto rapporto tra l e v , pari a 539,93, che tiene di gran lunga in sicurezza la struttura.

Il modulo di resistenza è pari a 448,53 cm^3.

La sezione che sceglierò in base al modulo di resistenza, sarà una IPE 300.

 

 

Legno

Prendo in considerazione gli stessi carichi dell’esercitazione precedente, ed eseguo l’analisi dei carichi per la mensola , cercando di inserire quei valori che permettono di ottenere  l/v > 250

 

Calcestruzzo armato

Considerando uno sbalzo di 4 m, riesco ad ottenere un giusto rapporto tra l e v , pari a 539,93, che tiene di gran lunga in sicurezza la struttura.

Il modulo di resistenza è pari a 448,53 cm^3.

La sezione che sceglierò in base al modulo di resistenza, sarà una IPE 300.

 

Acciaio

Considerando uno sbalzo di 4 m, riesco ad ottenere un giusto rapporto tra l e v , pari a 539,93, che tiene di gran lunga in sicurezza la struttura.

Il modulo di resistenza è pari a 448,53 cm^3.

La sezione che sceglierò in base al modulo di resistenza, sarà una IPE 300.

 

Osserviamo il comportamento dei carchi di un solaio di dimensioni scelte arbitrariamente. Calcoliamo quindi la dimensione delle travi del solaio, procedendo con tre tipi di solai: legno, c.a e acciaio.

La dimensione della luce e dell’interasse è rispettivamente di 5 m e 6 m, di conseguenza l’area maggiormente sollecitata è quella centrale pari a 30 mq ( data dal prodotto di luce e interasse stessi). Questa è anche l’area soggetta a maggior sforzo flettente.

 

 

Analizziamo in seguito il carico distribuito (KN/mq) dei materiali che compongono ogni tipo di solaio.

 

Avremo tre tipi di carico.

Due di questi, sono pertinenti ai materiali che compongono strettamente il solaio:

qp : carico permanente, carico degli elementi presenti nel solaio con funzione non strutturale.  

qs : carico degli elementi stutturali

 

Il terzo dipende dalla destinazione d’uso dell’edificio:

qa: carico accidentale , dato da Normativa tecnica.

 

Procediamo al calcolo dei carichi: quelli di cui possiamo calcolare noi il valore sono quello permanente e strutturale, con la seguente formula:

 

qp/ qs = (peso specifico del materiale *volume) / area analizzata

L’area che prendiamo in considerazione è pari a 1mq.

 

Mentre il carico distribuito di tipo accidentale è legato al tipo di destinazione d’uso che daremo al nostro edificio ed essendo dato da Normativa, è un valore tabellato.

Per la destinazione d’uso residenziale qa è pari a 2 KN/mq.

 

SOLAIO IN LEGNO 

 

Il solaio esaminato è costituito dai seguenti strati:

 

Trave portante , il cui dimensionamento è lo scopo dell’esercizio

Travetti , di larghezza 10 cm distanti 40 cm l’uno dall’altro con un peso specifico di 5 KN/m^3

strato di tavolato alto 10 cm con peso specifico di 6 KN/m^3

caldana 5 cm, peso specifico 25 KN/m^3

sottofondo 2 cm , peso specifico 18 KN/m^3

pavimentazione 2 cm , con un peso pari a 0,4 KN/m^2

 

Anche in questo caso si effettuano i calcoli dei carichi , suddividendoli in carichi strutturali, permanenti non strutturali e accidentali.

 

Carichi strutturali ( qs) :

2 travetti : 2*0,010 m^3/m^2 * 5 KN/m^3 = 0,1 KN/m^2

tavolato 0,02 m^3/m^2 * 6 KN/m^3 = 0,12 KN/m^2

 

Qs: 0,22 KN/m^2

 

Carichi permanenti non strutturali ( qp) :

pavimento : 0,04 KN/m^2

cls alleggerito : 0,02 m^3/m^2 * 18 KN/m^3= 0,36 KN/m^2

caldana : 0,05 m^3/m^2*25 KN/m^3= 1,25 KN/m^2

Qp: 1,65 KN/m^2

 

A questi valori si aggiungono i :

tramezzi 1 KN/m^2

Impianti 0,5 KN/m^2

 

 

Carichi accidentali (qa)

 

In questo caso , da valore tabellato , il carico accidentale che assegno al solaio, ipotizzando che la destinazione d’uso sia questa volta una biblioteca , è di 6 KN/m^2.

 

Inserisco i valori nella tabella che calcola autonomamente , con i calcoli preimpostati nel file, il valore del carico complessivo considerando il coefficiente di sicurezza, il momento agente , considerando la luce di 6 m .

 

Inserisco una base e ricavo così un’altezza minima.

Dopo aver scelto una base di 35 cm posso ottenere un’altezza minima di 57,70 cm che approssimo a 60 cm . 

 

Per effettuare la verifica , calcolo ora il peso della trave da inserire nella tabella.

 

Trave in legno lamellare GL24c, con Peso specifico = 3,8 KN/m^3, area = 2100 cm^2

Peso proprio trave= 3,8 KN/m^3*0,21 m^3/m^2 = 0,798 KN/m^2

 

Ora completo il calcolo del carico, inserendo il peso proprio della trave nel calcolo del carico complessivo , ignorando l’interasse, e moltiplicando per il cofficiente di sicurezza 1,3.

 

Data la nuova altezza di 58,23 dal calcolo di verifica, siccome tale altezza si mantiene al di sotto di 60 cm , considero la trave verificata. Sarà dunque sufficiente il profilo scelto prima.  

 

SOLAIO IN ACCIAIO 

 

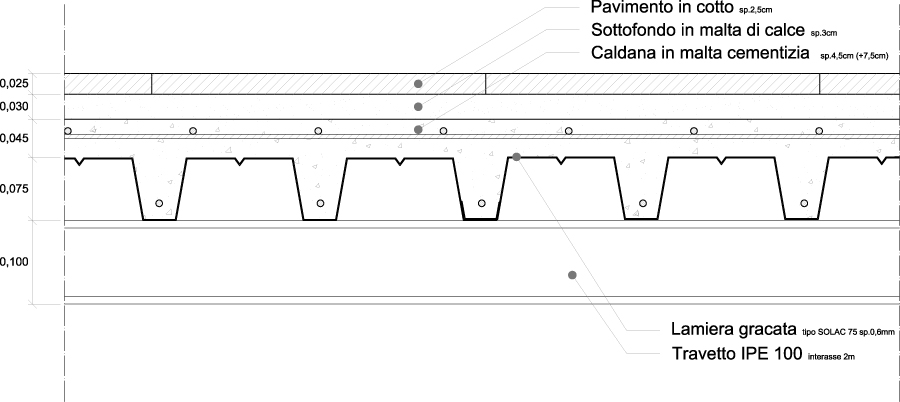
Ipotizzo di avere un solaio così composto:

 

Pavimento in cotto spesso 2 cm con peso pari a 0,4 KN/m^2

strato calcestruzzo alleggerito 8 cm con peso specifico pari a 18 KN/m^3

Getto in calcestruzzo 12 cm con peso specifico pari a 25 KN/m^3

lamiera grecata 0,8 mm con peso pari a 0,10 KN/m^2

trave secondaria con area pari a 16,4 cm^2 con peso specifico pari a 78,5 KN/m^3

trave principale

controsoffitto in fibra materiale con spessore di 2 cm e peso specifico di 13 KN/m^3

 

 

Per effettuare un dimensionamento della trave innanzitutto faccio un’analisi dei carichi , suddividendoli in carichi strutturali , permanenti e accidentali ( moltiplicati per i corrispettivi coefficienti di riduzione : 1,3 per i carichi permanenti e strutturali e 1,5 per i carichi accidentali).

 

Carichi strutturali :

 

- 2 Travetti IPE 140: 2 x 0,00164 m³/m² x 78,5 kN/m³ = 0,258 kN/m²

 

- Lamiera grecata: 0,08 kN/m²

 

- Getto di completamento in cls: 0,12 m³/m² x 25 kN/m³ = 3 kN/m²

 

Q_Stot= 3,338  kN/m²

 

Carichi permanenti (q_p):

 

- Pavimentazione in cotto: 0,4 kN/m²

 

- Massetto in cls alleggerito: 0,08 m³/m² x 18 kN/m³ = 1,44 kN/m²

 

- Controsoffitto: 0,02 m³/m² x 13 kN/m³ = 0,26 kN/m²

A questi carichi si aggiungono poi prendendo i dati dalla normativa:

- Tramezzi: 1 kN/m²

- Impianti: 0,5 kN/m²

Q_Ptot= 3,6 kN/m²

 

Carichi accidentali (qa )

I carichi accidentali variano a seconda della destinazione d’uso dell’edificio e sono dati da Normativa.

Il caso nostro ,ipotizzando un uso residenziale , richiede un carico accidentale pari a 2 KN/m^2.

 

Assegno alla trave una classe di resistenza, in questo caso la classe scelta è 275, con cui posso conoscere il momento ( 270,43 KN*m) e il modulo di resistenza.

Avendo ottenuto un Wx pari a 1323,41 , posso adottare una trave IPE 450, con Wx uguale a 1500 cm^3.

 

Siccome nei calcoli preliminari avevamo trascurato il peso proprio della trave , posso adesso sistemare i calcoli introducendo tra i carichi della struttura il peso proprio della trave (moltiplicato per il coefficiente di sicurezza 1,3 ma non per l’interasse). 

TRAVE IPE 450 ( Area 84,50 cm^2) : 0,008450 m^3/m^2 * 78,5 KN/m^3= 0,6633 KN/m^2

 

Qtot = 60,097 + (0,6633*1,3) = 60,95 KN/m

 

Con il nuovo risultato del modulo di resistenza Wx, la trave risulta avere una dimensione sufficiente per rientrare nella sicurezza , in quanto il nuovo Wx, 1147,14 cm^3 è al di sotto del Wx scelto in precedenza. Tale profilo risulta dunque adatto.

 

 SOLAIO IN CEMENTO ARMATO

 

 

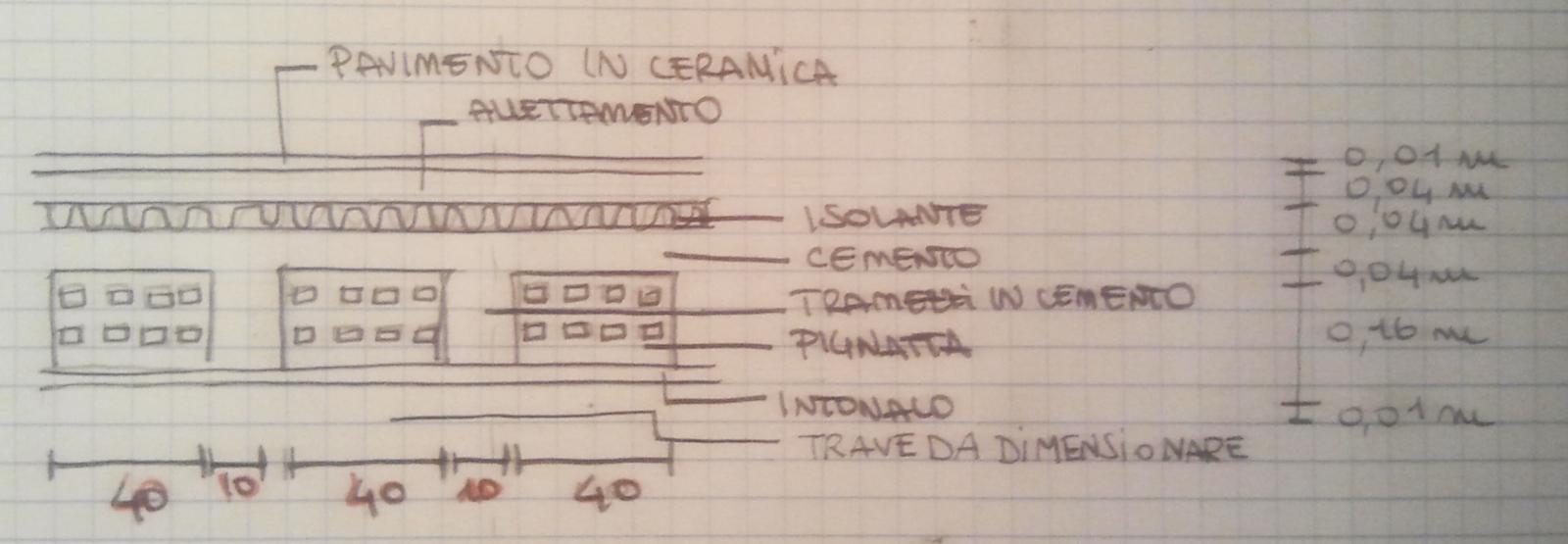
Il solaio in cemento armato che ho scelto è composto da una stratigrafia così costituita:

 

 

Eseguo il calcolo per conoscere il carico dei materiali che sono sostenuti dalla trave, in modo tale da definire quale sia effettivamente la dimensione giusta delle travi.

Separo dunque i valori dei carichi strutturali da quelli permanenti andandone a calcolare il valore , considerando per ciascun materiale il relativo peso specifico.

 

Carichi strutturali  (qs)

 

travetti : (0,1m*2*0,16m *1m)/1m^2 * 25 KN/m^3= 0,8 KN/m^2

getto caldana : (0,04m *1m*1m)/1m^2* 25 KN/m^3 = 10 KN/m^2

 

Carichi permanenti non strutturali (qp)

 

qp= (0,4m*2*0,16*1)/1m^2 * 5KN/m^3 + (0,04m*1m*1m)/1m^2*16 KN/m^3 + (0,04m*1m*1m)/1m^2 *3,5 KN/m^3 + (0,01m*1m*1m)/1m^2 * 18 KN/m^3 + (0,01 m *1m *1m )/ 1m^2 *0,4 KN/m^3= 1,604 KN/m^2

 

Vado dunque a inerire/determinare i valori mancanti nella tabella.

Classe di resistenza dell’acciaio da armatura : 450 Mpa

Classe di resistenza del calcestruzzo : 40 Mpa

Base trave ipotizzata : 30 cm

Delta : 5 cm

 

Bisogna inserire i valori nelle rispettive caselle affinchè il programma possa fornire un’altezza preventiva della trave

.

 

In questo caso è pari a 61,76 cm.

 

A questo punto è opportuno fare la verifica del peso della trave inserendo il peso proprio nella tabella. Inserisco dunque il carico della trave nel calcolo dei carichi strutturali. Considero il peso della trave dato dal suo volume per il peso specifico ( e moltiplico per il coefficiente di sicurezza dei carichi strutturali 1,3 ).

Di conseguenza l’altezza della trave sarà ricalcolata aumentando il suo valore .

La nuova altezza è 70,08 cm .

Per stare in sicurezza si dovrebbe scegliere un’altezza arrotondata per eccesso al valore appena più alto a quello trovato, multiplo di 5. In questo caso è talmente piccolo il valore decimale che corro il rischio di arrotondarla a meno.

 

Sceglierò dunque una trave con sezione di 70 x 30 cm. 

Abbiamo realizzato con il programma SAP una trave reticolare.

 

Possiamo realizzare sistemi di travature con SAP per osservare il comportamento di strutture già realizzate in precedenza tramite l’ausilio di alcuni programmi di supporto ( come Rhinoceros o Autocad).

Oppure possiamo creare la struttura all’interno del programma.

 

Scelgo la seconda opzione. 

Creo un nuovo modello.  Scelgo di lavorare su un sistema di riferimento a griglia, dato da “gril only”.

Qui posso decidere a che distanza porre le linee che compongono la griglia e di quante linee sarà composta la griglia stessa.

Questi parametri li decido nella finestra che si apre subito dopo.

Impongo quindi un valore 2 per l’asse x, y e z, a una distanza uguale per i tre assi pari a 6.

Servendomi del comando draw frame/ Cable , posso cominciare a disegnare la struttura direttamente sulla griglia. Comincio con il disegno di un singolo elemento .

Ripeto l’elemento base, tramite il comando copia (CTRL-C) –incolla (CTRL-V) , fino ad ottenere una trave di dimensioni abbastanza estese e verosimili , con la forma di un grande rettangolo.

Dopo aver terminato la trave, seleziono tutto e clicco edit---> edit points ---> merge joints , per  unire i punti di tutta la struttura , e in particolare quelli che potrebbero essersi sovrapposti nel passaggio precedente.Devo adesso sciogliere i nodi , ovvero separare le aste nei punti di incontro, i nodi appunto.

Questo perchè in quei punti ci sono le cerniere , che permettono la rotazione e il momento è nullo.

Bisogna dunque selezionare le aste, cliccare il comando assign ---> frame ---> Releases/ Partial Fixity; spunto quindi le voci Moment 2-2 e Moment 3-3 sia nella casella start che end (per imporre che il momento sia nullo sia all’inizio che alla fine di tutte le aste).Assegno adesso i carichi puntuali sulla trave.

Per cominciare seleziono i nodi della trave su cui decido di porre i carichi puntuali (F).

Assign > Joint loads >  Forces

Load pattern Name --->  Rinominare es. F

                 Self Weight multiplier ---> 0 .(Vuol dire che Non prendo in considerazione il peso proprio della struttura. )

                 Add New load pattern

Load pattern Name ---> F ( Seleziono quindi il carico che ho creato nel passaggio precedente)

Scelgo il peso del mio carico : Force Gobal z (asse verticale) : - 10 ( il – indica che il carico è rivolto verso il basso)

Ora bisogna inserire i vincoli:

Clicco il comando assign ---> Joints--- > Restraints

Scelgo il vincolo tra quelli proposti nella cartella.

Nel mio caso, ho scelto di inserire le cerniere , clicco dunque sull’icona della cerniera --> ok

La posiziono dove voglio che si trovi. E continuo con la stessa operazione finché non posizioni i vincoli necessari , 6 in tutto.Ora bisogna inserire i materiali :

Assign ---> frame ---> frame section ---> Add new property

Frame section Type (materiale) ---> Steel ( acciaio )

Add a steel section ---> Pipe ( tubolare)

Section Name ( Nome della sezione ) --> Es. Tubolare

 

Infine avvio l’analisi

Do not run --> per Deal e Modal di cui non si vuole fare l’analisi

Run Now per conoscere l’analisi di F ( quella che mi interessa). 

Da questa , posso osservare le deformazioni della struttura, con l’immagine delle deformazioni.

Posso inoltre conoscere i grafici delle sollecitazioni, e sapere il valore numerico delle sollecitazioni strutturali.

Esporto quindi la tabella che indica le sollecitazioni e le loro intensità. Da questa posso osservare come gli sforzi assiali siano tutti diversi da zero ( a meno che non ci siano delle aste scariche) mentre, i tagli e i momenti sono tutti uguali a zero.

Scelgo ordinare, infine,( in ordine decrescente ), i valori degli sforzi assiali ( P nella tabella), in modo da conoscere quali sono le aste più sollecitate e quali meno.  

Da qui emerge che lo sforzo più rilevante che la trave sopporta è uno sforzo di tipo assiale, dve il più grande valore , come emerge dalla tabella è 547,516 KN. Si dovrà dunque dimensionare l'asta tenendo conto di questo valore principalmente.

Abbiamo realizzato con il programma SAP una trave reticolare.

 

Possiamo realizzare sistemi di travature con SAP per osservare il comportamento di strutture già realizzate in precedenza tramite l’ausilio di alcuni programmi di supporto ( come Rhinoceros o Autocad).

Oppure possiamo creare la struttura all’interno del programma.

 

Scelgo la seconda opzione. 

Creo un nuovo modello.  Scelgo di lavorare su un sistema di riferimento a griglia, dato da “gril only”.

Qui posso decidere a che distanza porre le linee che compongono la griglia e di quante linee sarà composta la griglia stessa.

Questi parametri li decido nella finestra che si apre subito dopo.

Impongo quindi un valore 2 per l’asse x, y e z, a una distanza uguale per i tre assi pari a 6.

Servendomi del comando draw frame/ Cable , posso cominciare a disegnare la struttura direttamente sulla griglia. Comincio con il disegno di un singolo elemento .

Ripeto l’elemento base, tramite il comando copia (CTRL-C) –incolla (CTRL-V) , fino ad ottenere una trave di dimensioni abbastanza estese e verosimili , con la forma di un grande rettangolo.

Dopo aver terminato la trave, seleziono tutto e clicco edit---> edit points ---> merge joints , per  unire i punti di tutta la struttura , e in particolare quelli che potrebbero essersi sovrapposti nel passaggio precedente.