blog di davide.notarangelo

 La terza esercitazione consiste nel progetto di una trave a sbalzo nelle tre tecnologie di costruzione più comuni (legno, acciaio, cemento armato), con l’ausilio di un foglio elettronico Excel.

Piante di carpenteria di riferimento per solaio in legno,cls e acciaio

La prima carpenteria rappresenta un solaio in cls e legno; la seconda un solaio in acciao.

La trave a sbalzo maggiormente sollecitata è quella sull’asse B, con un’ area di influenza pari a 12 m² (luce: 3m, interasse: 4m).

Lo scopo dell’esercitazione è verificare che la deformabilità della trave non provochi un abbassamento (spostamento verticale) maggiore di 1/250 della luce della trave stessa; il foglio Excel ci permettere di conoscere il valore dello spostamento verticale della trave allo stato limite di esercizio.

Nel caso di una trave a sbalzo, si prende in considerazione il modello statico della mensola

                                           

il cui momento massimo è dato dalla formula  M_max = ql²/2

CEMENTO ARMATO

Considero i valori dei carichi strutturali, permanenti ed accidentali relativi al calcestruzzo della prima esercitazione:

q_s= 3,23 kN/m²

q_p= 2,64 KN/m²

q_a= 2kN/m²  

I tre carichi vengono sommati, moltiplicati per i loro coefficienti di sicurezza e moltiplicati per l’interasse ottenendo q_u pari a 44,64 kN/m. Conoscendo la luce (3 m) , si ottiene il valore del Momento massimo di una mensola  pari a  200,86 KNm.

Per le armature scelgo un acciaio con coefficiente di resistenza caratteristica pari a f_yk=450 MPa e un calcestruzzo con resistenza a compressione pari a f_ck=60 MPa. Imposto una base b pari a 25 cm; i calcoli del foglio Excel mi danno un’altezza minima della sezione che ingegnerizzo a 40 cm. Di conseguenza, ho una sezione di 25 cm X 40 cm.

Dopo aver dimensionato la sezione, effettuo la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce.

Il procedimento, che è uguale in tutte e tre le tecnologie, si effettua allo SLE (Stato Limite di Esercizio) poiché la verifica è finalizzata a controllare che non vi siano spostamenti e deformazioni che possano limitare l’uso della costruzione, la sua efficienza e il suo aspetto.

A tal motivo i carichi incidenti sulla struttura vengono ricombinati seguendo la combinazione frequente, generalmente impiegata per gli stati limite di esercizio reversibili:

                                                               q_e= (G1 + G2 + ¥11 × Q1) × i

Nel cemento armato, il peso proprio dell’elemento strutturale veniva calcolato anche nella prima esercitazione, poiché era necessario verificare allo stato limite ultimo (SLU) che la sezione scelta fosse idonea a sopportare tutti i pesi gravanti su di sé anche dopo aver aggiunto il peso proprio. Dopo questa verifica, l’informazione relativa al peso verrà riutilizzata per calcolare il carico totale q_e.

Infine, per calcolare lo spostamento è necessario conoscere il modulo elastico del materiale E e il suo momento d’inerzia I_x

Calcolato il carico totale allo SLE q_e, specificato il modulo elastico E ed il momento di inerzia I_x, è ora possibile calcolare l’abbassamento massimo che è pari a:

                                                                        v_max = q_e* l⁴ / 8EI_x

e verificare che il rapporto tra la luce della trave e il suo spostamento massimo sia maggiore di 250, come imposto dalla normativa in base al tipo di elemento strutturale considerato:

                                                                             l / v_max ≥ 250

Lo spostamento verticale massimo è pari a 1,08 cm e il rapporto tra la luce e lo spostamento massimo è maggiore di 250.

 

LEGNO

q_s= 0,18 kN/m²

q_p= 3,74 KN/m²

q_a= 2kN/m²  

q_u pari a 35,376 kN/m

Conoscendo la luce (3 m) , si ottiene il valore del Momento massimo di una mensola  pari a  159,192 KNm

Dopo aver impostato il modulo elastico del materiale, scelgo una base di lunghezza pari a 25 cm; i calcoli del foglio Excel mi danno un’altezza minima della sezione che ingegnerizzo a 50 cm. Di conseguenza, ho una sezione di 25 cm X 50 cm. Dopo aver dimensionato la sezione, è necessario effettuare la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce.

Nel caso del legno, per quanto riguarda il calcolo del carico totale allo stato limite di esercizio, il peso proprio della trave viene trascurato in quanto è un materiale leggero.

                                                          q_e= (G1 + G2 + ¥11 × Q1) × i = 20 kN/m

Calcolato il carico totale allo SLE q_e, specificato il modulo elastico E ed il momento di inerzia I_x, è ora possibile calcolare l’abbassamento massimo che è pari a:

                                                                    v_max = q_e l⁴/ 8EI_x= 0,96 cm.

Di conseguenza:

                                                                             l / v_max> 250

 

ACCIAO

q_s= 1,18 kN/m²

q_p= 1,74 kN/m²

q_a= 2kN/m²

q_u pari a 28,576 kN/m

Conoscendo la luce (3 m) , si ottiene il valore del Momento massimo di una mensola  pari a  128,592 KNm

Dopo aver definito la resistenza del materiale, dal foglio Excel si ottiene un modulo di resistenza a flessione W_x,min pari a 490,99 cm³. Quindi è opportuno utilizzare come profilato una IPE 300 che ha W_x pari a 557,0 cm³ e I_x pari a 8356 cm⁴. 

Dopo aver dimensionato la sezione, è necessario effettuare la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce. Come per il cemento, anche per l’acciaio va considerato il peso proprio (0,422 KN/m); informazione che verrà riutilizzata per calcolare il carico totale q_e.

                                                    q_e= (G1 + G2 + ¥11 × Q1) × i = 16,102 kN/m

Calcolato il carico totale allo SLE q_e, specificato il modulo elastico E ed il momento di inerzia I_x, è ora possibile calcolare l’abbassamento massimo che è pari a:

                                                                   v_max = q_e l⁴/ 8EI_x= 0,929 cm.

Di conseguenza:

                                                                              l / v_max> 250

La travatura reticolare (o struttura reticolare) è una struttura composta da un insieme di aste vincolate ai nodi in modo da costituire un elemento resistente e indeformabile. La travatura reticolare ha tratto la propria origine dalla necessità di impiegare strutture sempre più leggere per superare luci sempre più grandi.

Nella seconda esercitazione ho dimensionato e analizzato una struttura reticolare tridimensionale con l’ausilio del software SAP2000 e di un foglio Excel.

In particolare, SAP2000 mi ha permesso di modellare una struttura reticolare e di ottenere, alla fine, i dati relativi agli sforzi assiali sulle singole aste; non troveremo, infatti, sollecitazioni di taglio e momento.

1. Avviato il programma, ho aperto un file New model, impostato l'unità di misura KN, m, C e scelto come spazio di lavoro Grid Only.

Ho creato una maglia rettangolare 6m x 8m composta da 12 campate 2m x 2m. Ho iniziato a modellare la mia struttura a base cubica collegando i vari vertici tra loro e controventando ogni singola faccia del cubo 

2.  il risultato è una struttura reticolare composta da 12 cubi di dimensioni 2m x 2m X 2m

3.  Ho completato la mia struttura assegnando, come vincolo esterno, una cerniera ai quattro spigoli inferiori e, tramite il comando Assign > Frame > Release partial fixity, ho trasformato tutti i nodi in cerniere interne.

4.  Successivamente ho assegnato il materiale (acciaio) alle aste della struttura, scegliendo un profilato a sezione circolare cava (Pipe)

5. cliccando su Define > Load pattern definisco un nuovo sistema di carichi inserendo un nuovo paramentro F con un Self Weight Multiplier uguale a 0.

6. Cliccando su Assigne > Joint loads > Forces assegno i carichi alla struttura, dopo aver selezionato esclusivamente i nodi superiori; la forza è pari a 100 kN (-100 kN in quanto è diretta verso il basso)

7.  Conclusa la prima fase di modellazione, si può procedere con l’analisi dei carichi selezionando esclusivamente la forza F

8. Ottengo così la struttura deformata e posso visualizzare i diagrammi (e i valori) dello sforzo assiale

9.  Cliccando su  Display > Show tables posso controllare i dati dell'analisi spuntando Analisys Results e selezionando il valore F

10. Infine esporto la tabella Element Forces - Frames in un file Excel per ottenere i dati utili al dimensionamento delle aste

Dopo un’operazione di “pulizia del file”, in cui ho eliminato i dati duplicati, ho ordinato i valori relativi allo sforzo normale dal più piccolo al più grande ed ho evidenziato i valori delle aste diagonali;  ora posso trasferirli nelle tabelle Excel preimpostate per trazione e compressione.

TRAZIONE

Prendo tutti i valori positivi dalla tabella esportata da Sap2000 e li incollo nel foglio Excel preimpostato nella sezione “acciao trazione”.

Per il dimensionamento delle aste, prendo in considerazione il valore massimo dello sforzo di trazione ed, in base a questo valore, il foglio Excel mi da un’area minima della sezione; quindi, dalla tabella dei profilati metallici circolari, scelgo una sezione con area maggiore rispetto all’area minima indicata.  

    

COMPRESSIONE

Prendo tutti i valori negativi dalla tabella esportata da Sap2000 e li incollo nel foglio Excel preimpostato nella sezione “acciao compressione”.

Per il dimensionamento delle aste compresse, prendo in considerazione:

1.    Valore massimo dello sforzo di compressione

2.    Area minima relativa all’asta soggetta allo sforzo di compressione maggiore

3.    Il valore massimo del momento d’inerzia minimo

Ingegnerizzando, verifico che il valore di lambda sia < 200.

In base a questi valori, per la mia struttura reticolare ho scelto un profilato metallico a sezione circolare cava di dimensioni 114,3 X 4,5 mm.

La prima esercitazione consiste nel progetto di una trave nelle tre tecnologie di costruzione più comuni (legno, acciaio, cemento armato), con l’ausilio di un foglio elettronico Exel.

Pianta di riferimento per il solaio in legno e in cemento armato

                     

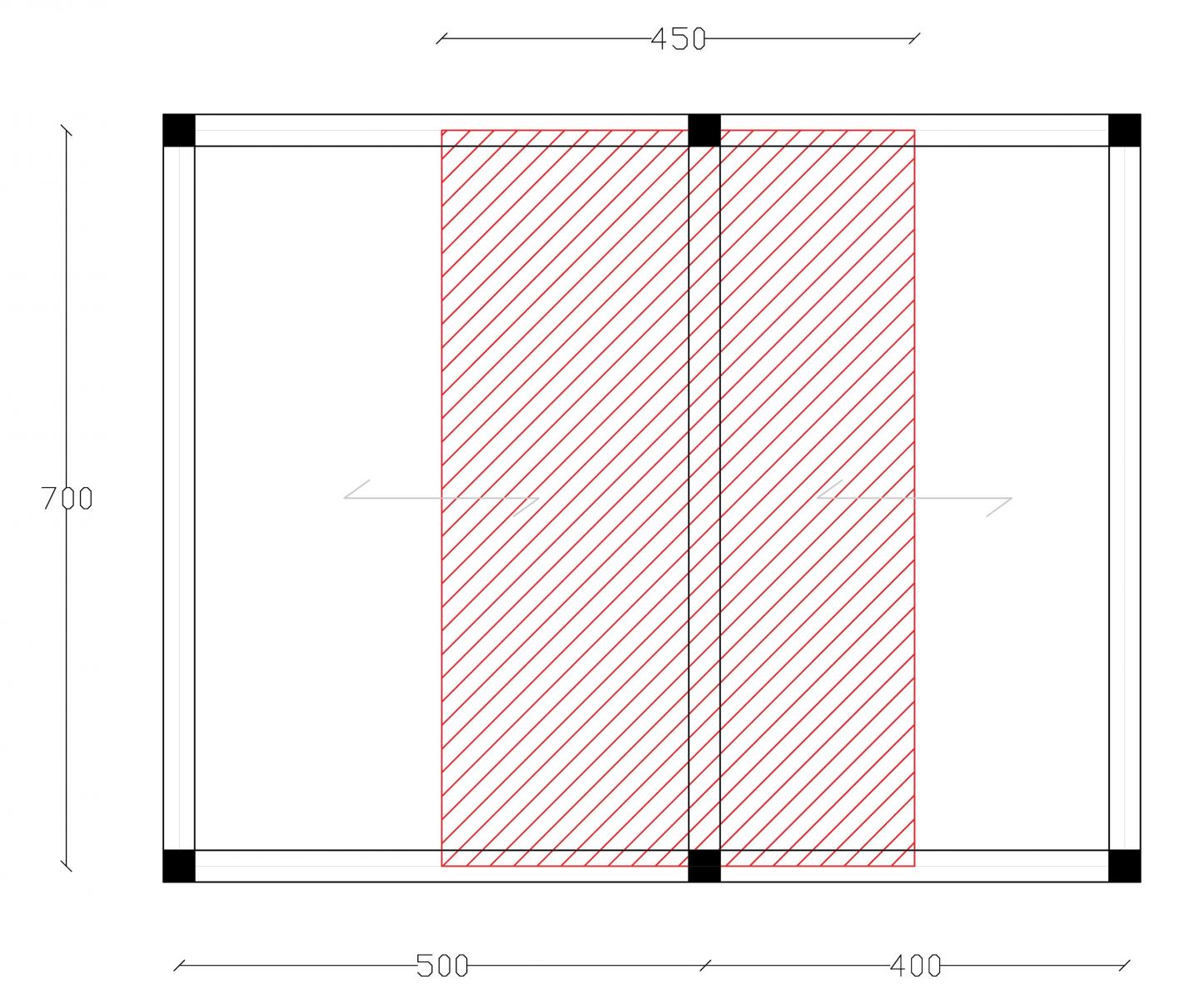
Pianta di riferimento per il solaio in acciao

     

SOLAIO IN LEGNO

Considerando la pianta di carpenteria di un solaio in legno, dimensiono l’altezza della sezione della trave centrale, ovvero quella maggiormente sollecitata (evidenziata nel disegno); l’area di influenza è pari a 31,5 m²  .

                                    

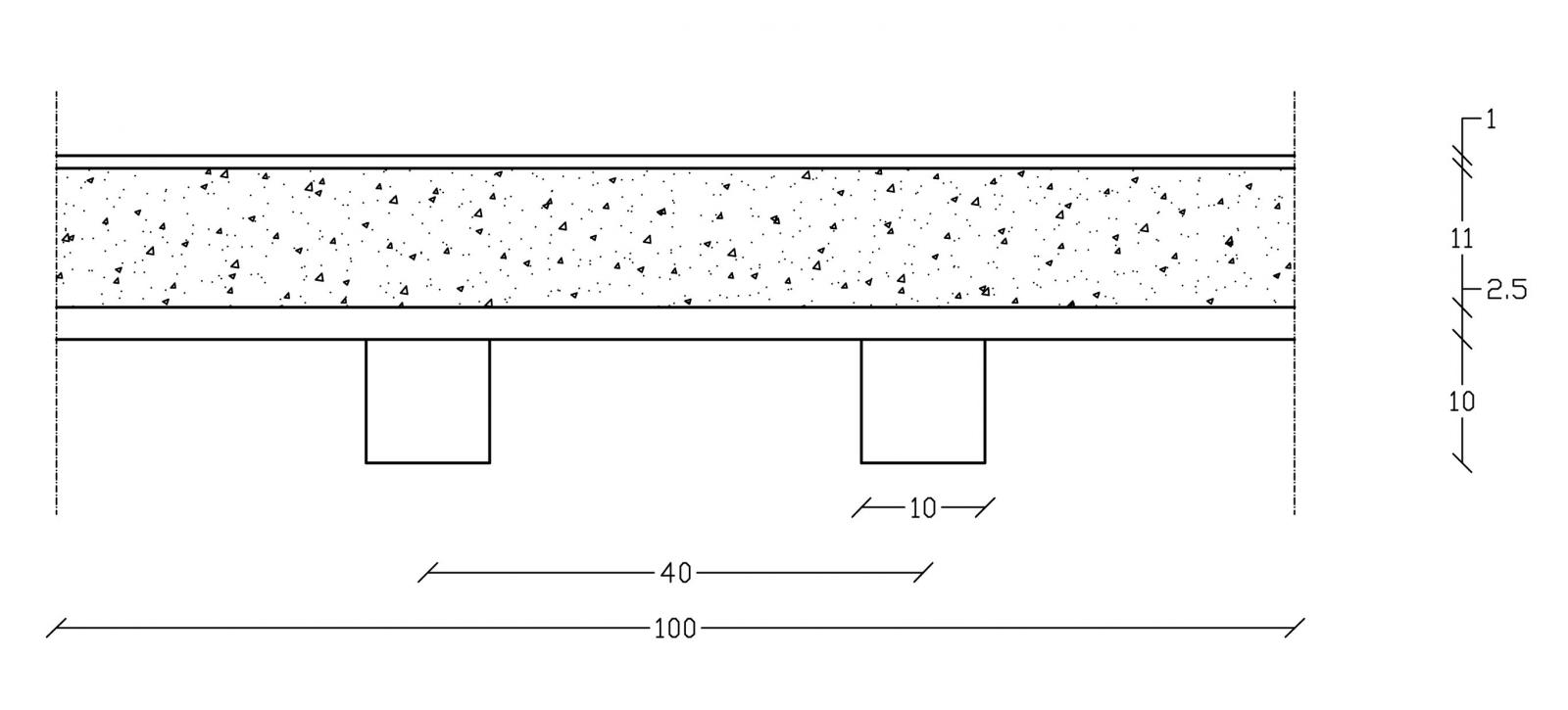
Disegnata la sezione “tipo”, calcolo i carichi agenti su 1 m² di solaio, considerando tre tipi di carichi: strutturali (q_s), permanenti (p_s) e accidentali (q_a).       

[Carico = Peso specifico X Volume]

Carico strutturale q_s   (carico dovuto al peso proprio di tutti gli elementi che svolgono una funzione portante):

• TRAVETTI in legno lamellare classe GL28H  (0,10m X 0,10m X 1m):

        2 [4 kN/m³ x (0,10 x 0,10 x 1) m³/m²]= 0,08 kN/m²       

• TAVOLATO in legno lamellare classe GL28H (0,025m X 1m X 1m):

        4 kN/m³ x (0,025 x 1 x 1) m³/m² = 0,1 kN/m²

                                                   q_s= 0,08 kN/m²  + 0,09 kN/m² = 0,18 kN/m²

 

Carico permanente q_p  (carico dovuto al peso proprio di tutti gli elementi che gravano sulla struttura portante per il suo intero periodo di vita e che non svolgono un ruolo strutturale):

• MASSETTO (spess. 0,11 m):

        18 kN/m³ x (0,11 x 1 x 1) m³/m²  = 2 kN/m²

• PAVIMENTAZIONE in Klinker (spess. 0,01 m): 0,24 kN/m²

• IMPIANTI : 0,5 kN/m²

• TRAMEZZI : 1 kN/m²

                                             q_p= 2 kN/m²  + 0,24 kN/m² + 1,5 kN/m²= 3,74 kN/m²

 

Carico accidentale q_a (carico regolato dalla normativa attualmente vigente: NTC2008- Norme tecniche per le costruzioni- D. M. 14 Gennaio 2008)

                                             q_​a= 2 kN/m²  (per l’ambiente ad uso residenziale)

 

I tre carichi vengono sommati:

• q_tot = q_s + q_p + q_a =( 0,18 + 3,74 + 2 ) kN/m² = 5,92 kN/m²

e moltiplicati per i loro coefficienti di sicurezza:

• ​q_tot = q_s + q_p + q_a =( 1,3*0,18 + 1,5*3,74 + 1,5*2 ) kN/m² = 8,84 kN/m²

Conoscendo il carico incidente su 1 m² di solaio e l’area del solaio portato dalla trave, possiamo ricavare il carico totale distribuito del solaio di area A (4,5m x 7m):

• ​q_totaleArea= 8,84 kN/m² x 31,5 m= 278,46 kN/m

Adesso, per trovare il valore del carico lineare incidente sulla trave, è necessario dividere il carico totale dell’Area per la luce della trave:

• q_trave = 278,46 kN / 7m= 39,8 kN/m

oppure moltiplicare il carico del solaio per l’interasse:

• ​q_u = (1,3*q_s + 1,5*q_p + 1,5*q_a)*i = 39,80 kN/m

Sapendo che la luce della trave è 7 m, si può ricavare il Momento massimo:

• M_max= ql²/8 = 243,76 kNm

FASE PROGETTUALE

In fase di progettazione, ho scelto di realizzare il solaio con legno lamellare GL28H, con resistenza caratteristica f_m,k=28 N/mm² (MPa), con classe di servizio 2 e classe di durata media, quindi k_mod =0,80.

                        

                              

           

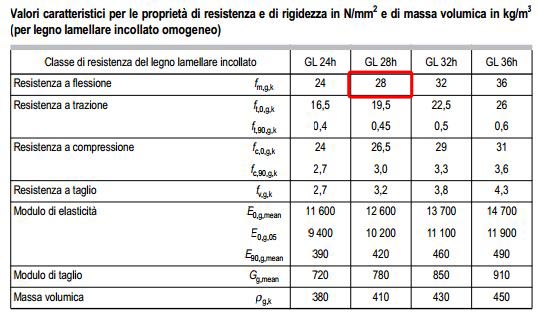
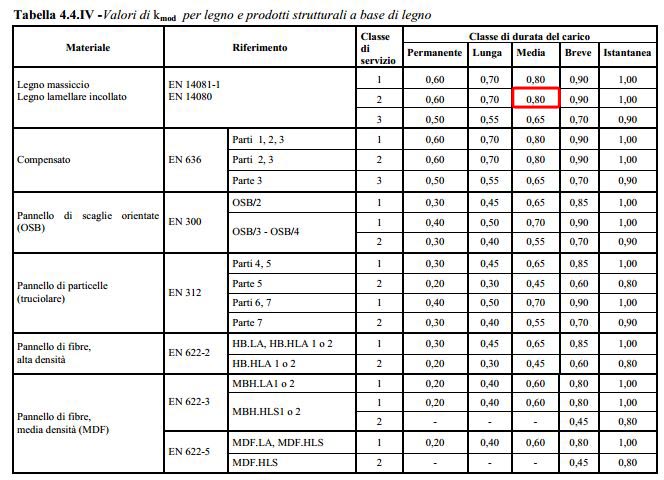
Calcolo, quindi, la resistenza di progetto f_d , e ricavo l’altezza della sezione della trave impostando la base b (35 cm).

La tensione di progetto viene calcolata, secondo la norma, mediante la relazione:

• f_d= k_mod * f_m,k / y_m = 0,80*28/1,45= 15,45 N/mm²

Una volta trovata h_min, è opportuno ingegnerizzare il valore in modo tale da trovare un valore dell’altezza superiore al valore minimo. Quindi, scelgo una trave a sezione rettangolare (35 x 55) cm.

     

VERIFICA

Considero nei calcoli svolti in precedenza il peso proprio della trave e lo sommo agli altri carichi:

• p_trave = (0,35 x 0,55 x 1) m³/m x 4 kN/m³ = 0,8 kN/m (moltiplicato per 1,3 = 1,04 kN/m)

Ottengo un nuovo valore di q_u e una nuova h_min

    

La scelta fatta in precedenza di utilizzare una trave a sezione rettangolare (35 x 55) cm è compatibile con i nuovi valori.

                                                                    La sezione è stata verificata

 

SOLAIO IN ACCIAIO

                                 

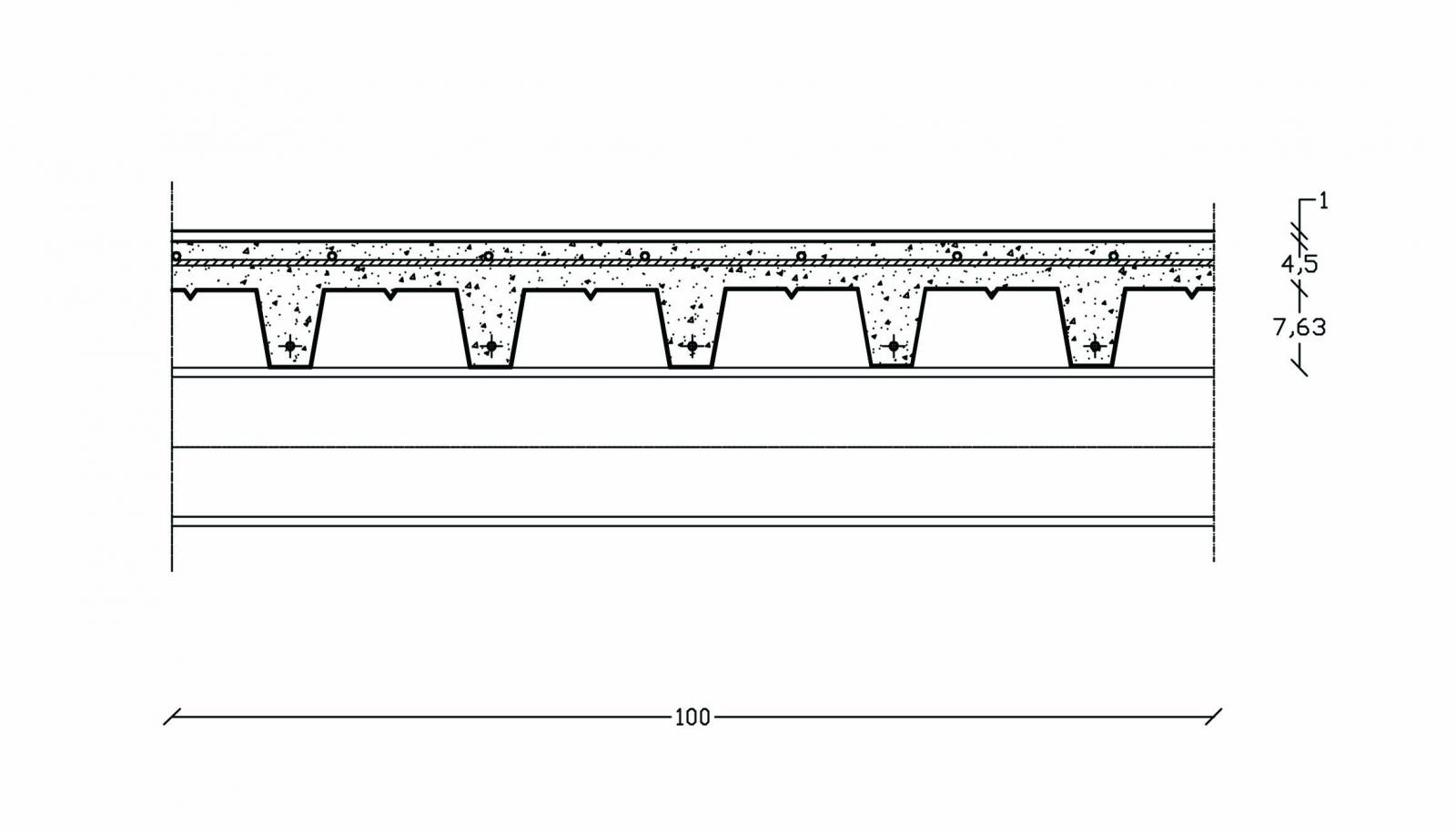
Carico strutturale q_s

• LAMIERA GRECATA: 0,10 kN/m²
• GETTO CLS: 24 kN/m³ x (0,045 x 1 x 1) m³/m² = 1,08 kN/m²

                                                         q_s= 0,10 kN/m²  + 1,08 kN/m² = 1,18 kN/m²

Carico permanente q_p

• PAVIMENTO: 0,24 kN/m²
• IMPIANTI : 0,5 kN/m²
• TRAMEZZI : 1 kN/m²

                                                         q_p= 0,24 kN/m² + 1,5 kN/m²= 1,74 kN/m²

Carico accidentale q_a

                                                        q_a = 2 kN/m²  (per l’ambiente ad uso residenziale)

 

Con il foglio Excel, i valori ottenuti vengono sommati tra loro per ottenere q_u (kN/m):

• q_u = (1,3*q_s + 1,5*q_p + 1,5*q_a)*i = 32,15 kN/m

FASE PROGETTUALE

In fase di progettazione, per questo solaio è stato scelto un acciaio con una resistenza caratteristica  f_m,k = 275 MPa (acciao S275). 

Dal foglio Excel si ottiene un modulo di resistenza W_x pari a 751,82 cm³; quindi è opportuno utilizzare come profilato una IPE 360 con un W_x pari a 904 cm³.

    

                 

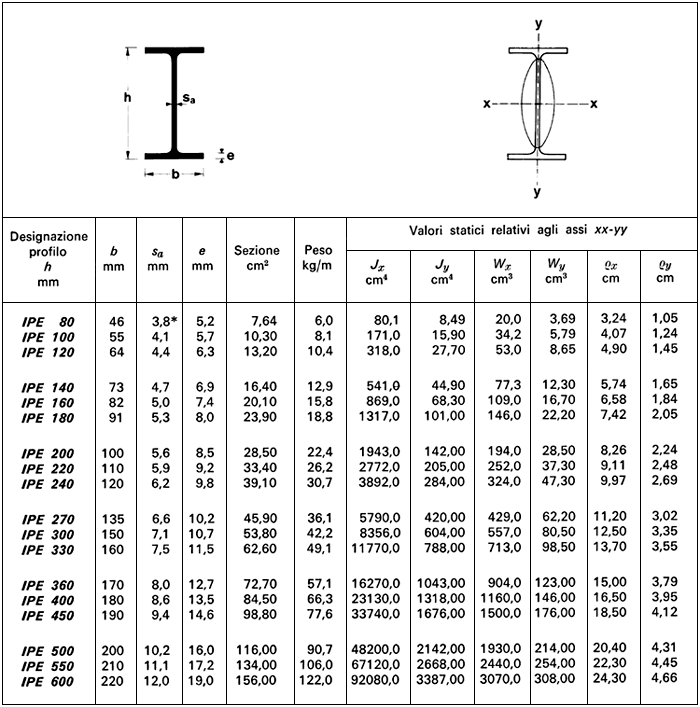
VERIFICA

Analogamente a quanto fatto per la trave in legno, anche per la trave in acciaio bisogna ricalcolare il valore di q_u tenendo in considerazione il peso proprio della trave.

Si aggiunge, quindi, ai carichi strutturali q_s  il peso p della trave moltiplicato per 1,3:

• p_trave = (0,00727 x 1) m³/m x 78,5 kN/m³ = 0,57 kN/m (moltiplicato per 1,3 = 0,74 kN/m )

     

Il risultato è compatibile con i valori W_x del profilato IPE 360 scelto inizialmente.

                                                                        La sezione è stata verificata.

 

SOLAIO IN CLS ARMATO

                                 

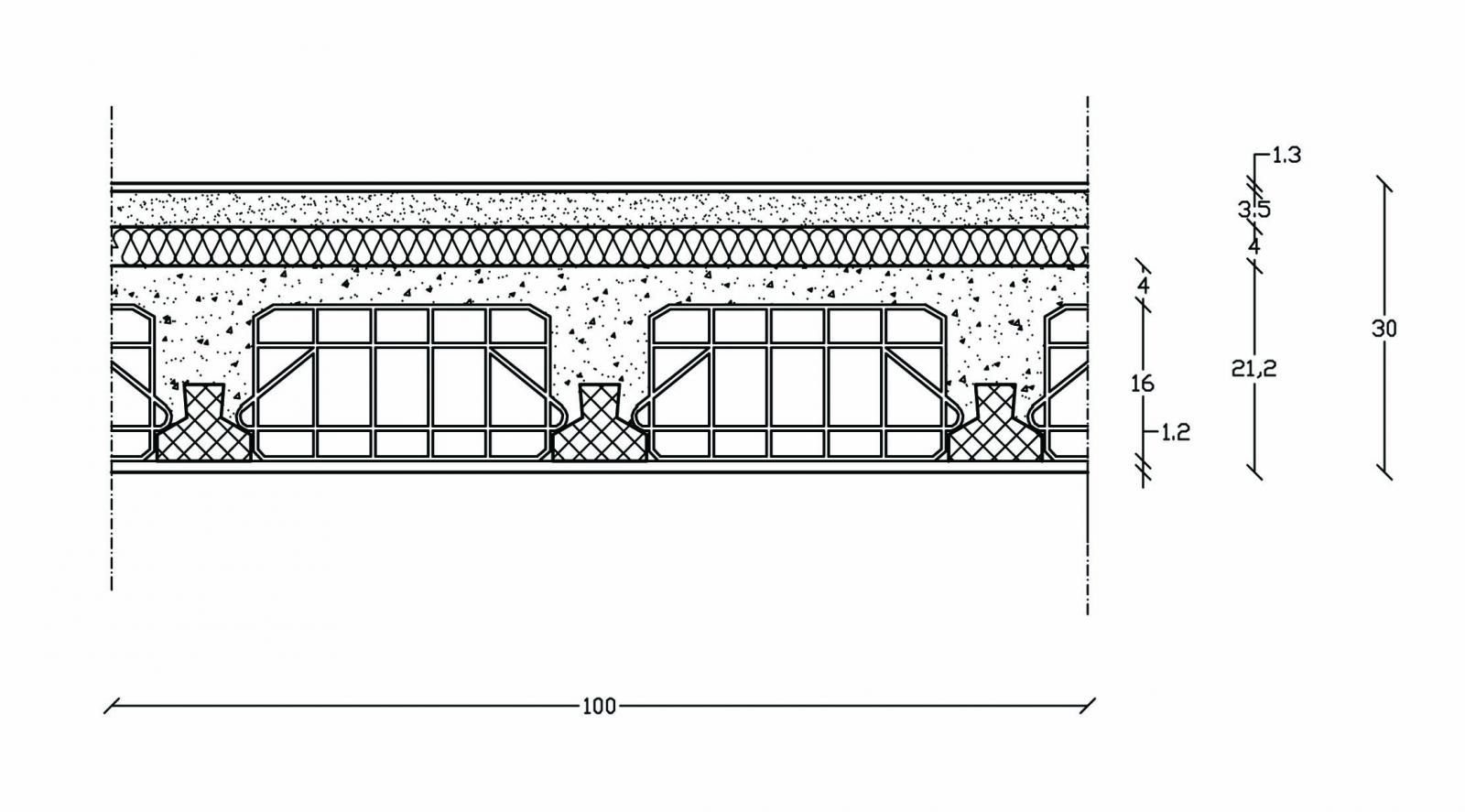
Carico strutturale q_s

• PIGNATTA di dimensioni (16 x 35 x 33) cm e peso specifico 0,08 kN/m²:  n°7 x 0,08 kN/m² = 0,56 kN/m²

• SOLETTA in cls altezza 4 cm e peso specifico pari a 24 kN/m³:  4 kN/m³ x (0,04 x 1 x 1) m³/m² = 0,96 kN/m²

• TRAVETTI in cls precompresso (14 x 17) cm:  3 [24 kN/m³ x (0,14 x 0,17 x 1) m³/m² = 1,71 KN/m²

                                        q_s= 0,56 KN/m²  + 0,96 KN/m² + 1,71 KN/m² = 3,23 KN/m²

 

Carico permanente q_p

• INTONACO spessore 1,2 cm e peso specifico pari a 16 kN/m³:  (0,012 x 1 x 1)m³/m² x 16 kN/m³ = 0,19 kN/m²

• ISOLANTE spessore 4 cm e peso specifico pari a 0,35 kN/m³:  (0,04 x 1 x 1)m³/m² x 0,35 kN/m³ = 0,01 kN/m²

• MASSETTO spessore 3,5 cm e peso specifico 20 kN/m³:  (0,035 x 1 x 1) m³/m² x 20 kN/m³ = 0,7 kN/m²

• PAVIMENTO: 0,24 KN/m²

• IMPIANTI : 0,5 KN/m²

• TRAMEZZI : 1 KN/m²

                     q_p= 0,19 kN/m² + 0,01 kN/m² + 0,7 kN/m² + 0,24 kN/m² + 1,5 kN/m²= 2,64 KN/m²

 

Carico accidentale q_a

                                                 q_a = 2 kN/m²  (per l’ambiente ad uso residenziale)

 

I valori ottenuti vengono sommati tra loro per ottenere q_u (kN/m):

• ​q_u = (1,3*q_s + 1,5*q_p + 1,5*q_a)*i = 49,75 KN/m

Conoscendo la luce (7 m),si ottiene il valore del Momento massimo di una trave appoggiata M_max = ql²/8 (307,57 KNm)

                                   

 

FASE PROGETTUALE

Il foglio di calcolo relativo al cemento armato ha bisogno di più informazioni per dimensionare l’altezza della sezione di una trave perchè si tratta di un materiale non omogeneo, composto da calcestruzzo e da acciaio.

Per questa ragione, in fase progettuale, è necessario scegliere sia la resistenza caratteristica dell’acciaio (f_yk) , che quella del calcestruzzo (f_ck).

Per le armature scelgo un acciaio con coefficiente di resistenza caratteristica pari a f_yk=450 MPa e un calcestruzzo con resistenza a compressione pari a f_ck=60 MPa. Imposto una base b pari a 25 cm.

Si ottiene un H_min pari a 44,70 cm; ingegnerizzando possiamo scrivere H = 50 cm.

     

Quindi la sezione finale della trave in cls sarà (25 x 50) cm.

VERIFICA

Anche per la trave in cls armato bisogna ricalcolare il valore di q_u tenendo in considerazione il peso proprio della trave.

Si aggiunge, quindi, ai carichi strutturali q_s  il peso p della trave moltiplicato per 1,3:

• p_trave = (0,25 x 0,50 x 1)m³/m x 25 kN/m³ = 2,81 kN/m (moltiplicato per 1,3 = 4,06 kN/m)

Ottengo un nuovo valore di q_u (54,28 kN/m) e una nuova H_min (46,28 cm)

    

L’ipotesi di utilizzare una trave a sezione rettangolare di dimensioni (25 x 50) cm era corretta.

                                                                   La sezione è stata verificata.

 

 

 

 

 

Presente! ;)