Trave appoggiata in acciaio
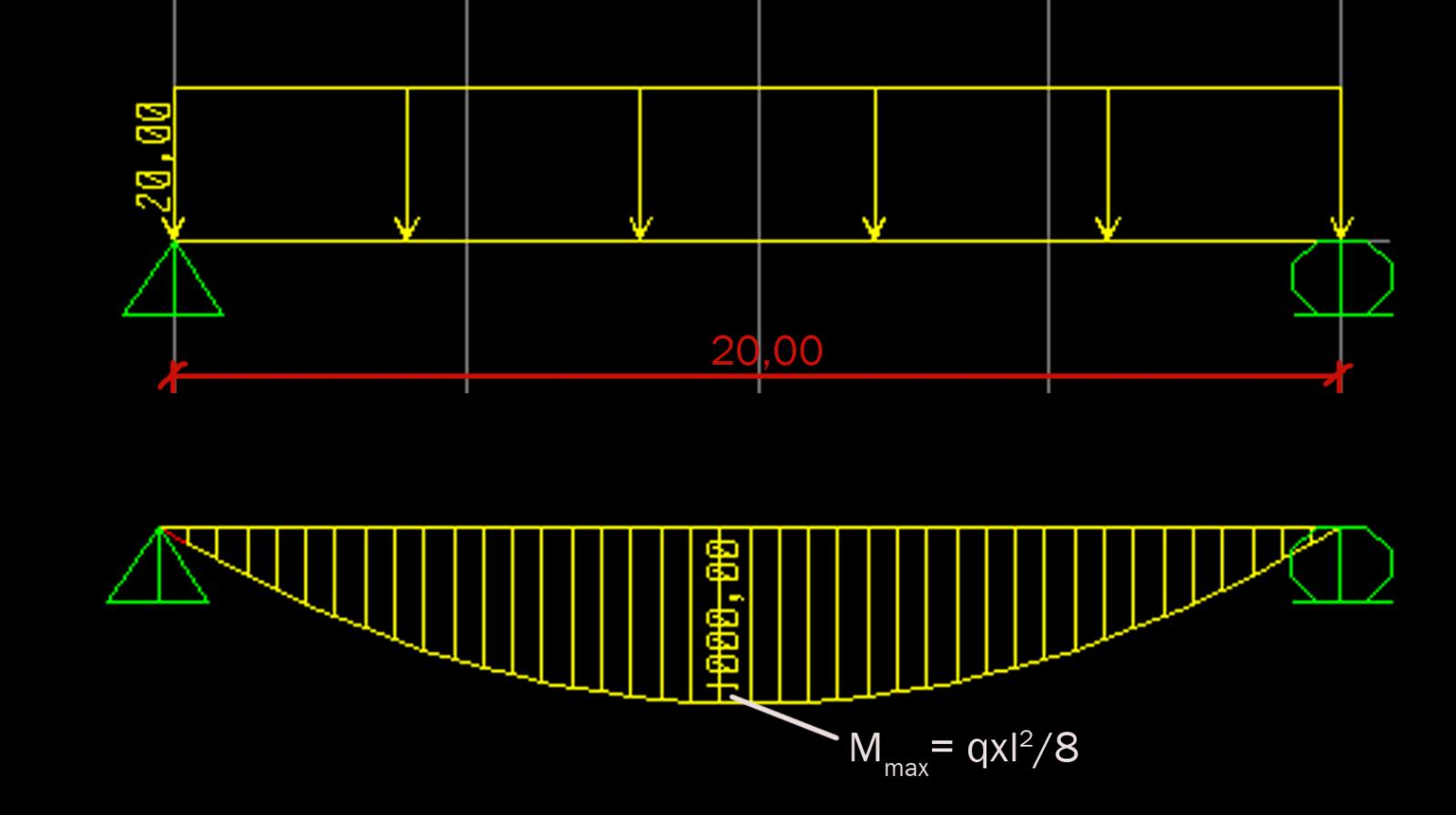
Il momento massimo della trave è in mezzeria ed è uguale a (qxl2 )/8
Mmax= 20x202/8 = 1000 kNm
Visto la luce della trave utilizzo un acciaio speciale, più resistente.
Fe510 fyk= 355 MPa v (coefficiente di sicurezza)=1,15
Wx = Mmax / (fyk/v) = 1000/ (355*1000/1,15) = 0,003239 m3 = 3239 cm3
Il profilario preso in esame non prevede sezioni per moduli di resistenza di tali dimensione.
Considero quindi il più grande presente : IPE600 con Wx = 3069 cm3
Trave reticolare
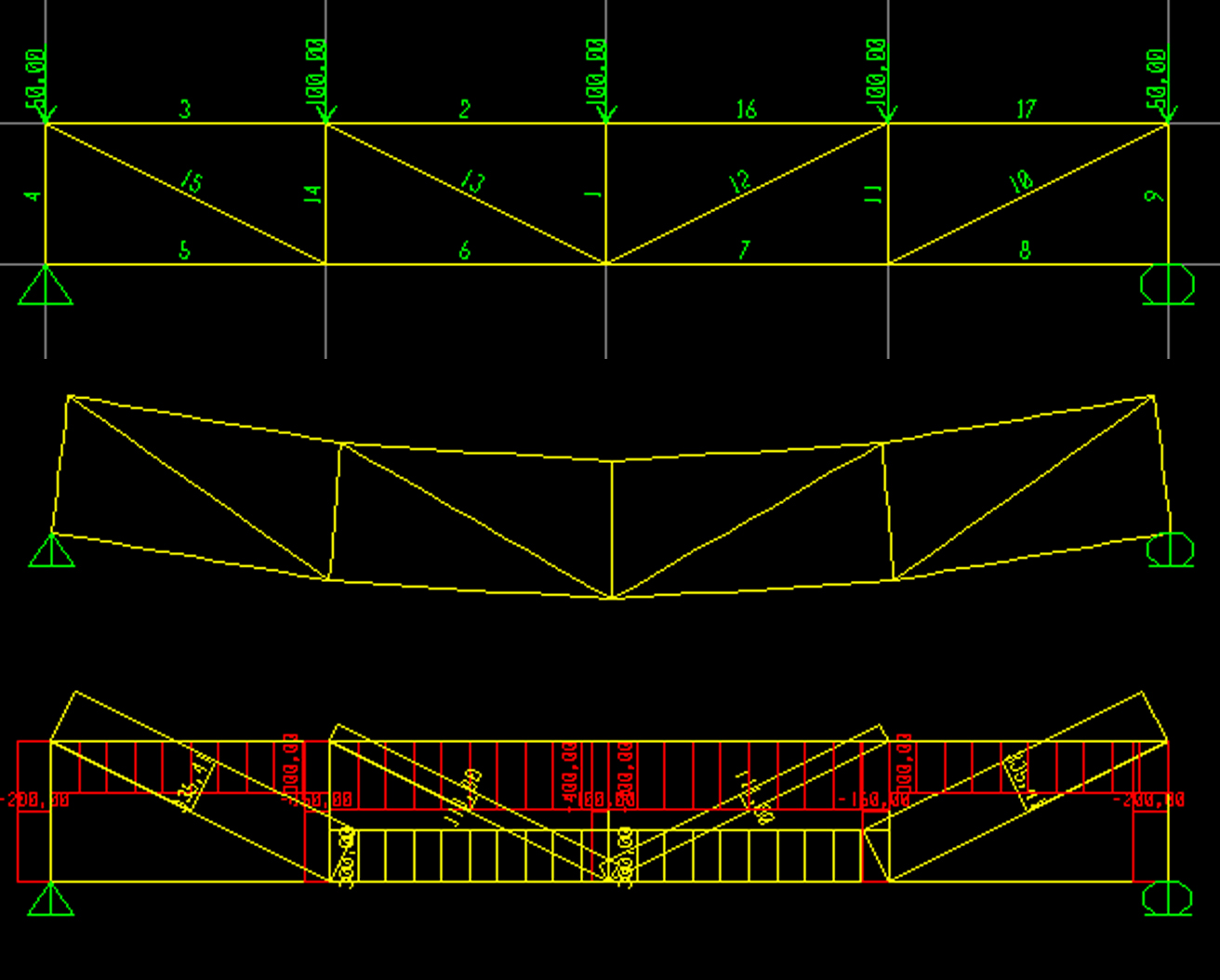
Il modello elaborato su SAP mi conferma che, essendo una trave reticolare, la struttura non è sollecitata a flessione ma solo lungo le direzioni delle aste.
Per dimensionare la struttura considererò le aste più sollecitate rispettivamente a trazione e compressione.
ASTA 15-10 N(Trazione) = 335 kN ASTA 2-16 N(compressione) = 400 kN
Fe510 fyk= 355 MPa v (coefficiente di sicurezza)=1,15
ASTA SOLLECITATA A TRAZIONE
Amin = N(T)/ σadm = 335000 / 308,7 = 1085m m2 = 10,85 cm2
Ipotizzo un profilo tubolare con diametro 114,3 mm e spessore 3,6 mm (A=12,50cm2)
ASTA SOLLECITATA A COMPRESSIONE
Imin= (C x ν x l²)/(π² x E)= (400 x1.2x(500)²) / (π²x21000 ) = 554,85 cm4
Ipotizzo un profilo tubolare con diametro d=168 mm e spessore s=3,2 mm (I=566cm4)
Verifico la snellezza del profilo
ρ= √ I / A = √ 566/16,60 = 5,83 cm
λ = lo / ρmin = 500/5,83 = 85,76
Trave Vierendeel
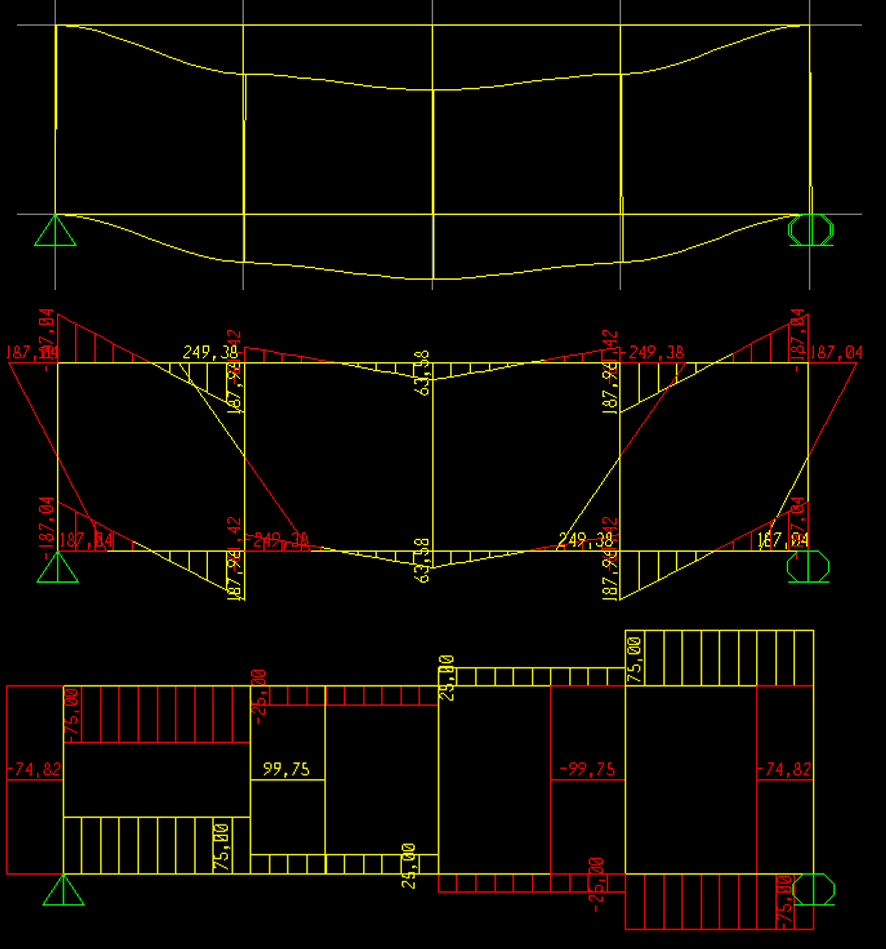
Dal modello sviluppato su SAP ricavo l'asta più sollecitata.
Dal momento che sulla struttura si sviluppano sia sollecitazione flessionali che di trazione e compressione, nel primo dimensionamento di massima a flessione imporrò una maggiorazione ipotetica del 50%.
Wx = Mmax /1,5σadm = 187000/1,5x308,7 = 403,84 cm3
Adotto IPE 270 con Wx= 428,9 cm3 A=45,95 cm2
A questo punto verifico a pressoflessione se la tensione di progetto è minore di quella ammissibile
Mmax/Wx + Nmax/A < σadm
σd =1870/428,9 + 7500/45,95 = 167,58 MPa < σadm
Commenti recenti