Scelgo una pianta di carpenteria e dimensiono la trave a sbalzo più sollecitata nei tre materiali scelti: cemento armato, acciaio e legno. Partendo dal solaio in figura evidenzio la trave più sollecitata; essa infatti ha un’area d’influenza maggiore rispetto alle altre pari a 4 m x 3 m= 12 m².


Prendo in considerazione i solai utilizzati nella prima esercitazione.
SOLAIO IN CEMENTO ARMATO
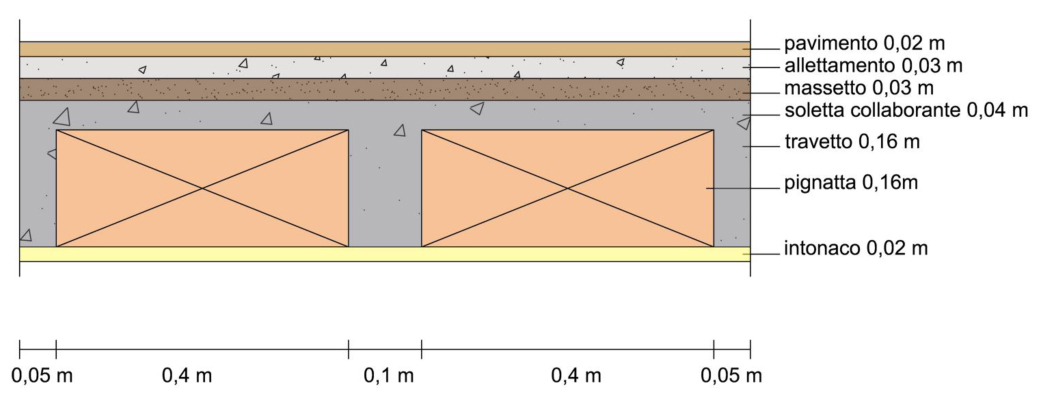
Analizzo il carico strutturale qs, il carico permanente qp e il carico accidentale qa.
Carico strutturale qs = 2,378 KN/m²
Carico permanente qp = 3,54 KN/m²
Carico accidentale qa = 2 KN/m²
Dopo aver trovato i valori dei carichi qs, qp e qa, questi si inseriscono nella tabella Excel. Il carico totale ultimo qu si troverà moltiplicando il carico strutturale per un coefficiente di sicurezza pari a 1,3 e i carichi permanente e accidentale per un coefficiente di sicurezza pari a 1,5. La combinazione di questi carichi deve essere poi moltiplicata per l’interasse della trave e si troverà così il carico a metro lineare agente sulla trave qu.
Essendo la trave in oggetto una trave a sbalzo, il momento massimo si trova nella sezione di incastro ed è M= ql²/2, quindi pari a M=205,23 KNm.

La resistenza caratteristica delle armature è pari a fyk= 450 Mpa, mentre per il calcestruzzo scelgo un C35/45 con fck = 45 Mpa. Ponendo la base b=30 cm si ottiene un’altezza ingegnerizzata pari a H= 45 cm.
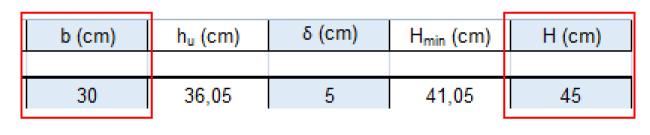
Vengono poi effettuati dei calcoli per verificare se la sezione con l’altezza ingegnerizzata H è in grado di portare i carichi calcolati in precedenza e il peso proprio della trave. Di conseguenza al qu ottenuto precedentemente si somma il peso unitario della trave moltiplicato per un coefficiente di sicurezza 1,3. Se l’altezza che si ottiene con il nuovo dimensionamento è più piccola dell’altezza ingegnerizzata H, la sezione risulterà verificata.
Dopo aver dimensionato la sezione, bisogna effettuare la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce e questo calcolo si effettua allo SLE (Stato Limite di Esercizio).
I carichi vengono ricombinati seguendo la combinazione frequente e viene aggiunto il peso proprio della trave:
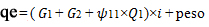
Inserito il valore del modulo elastico E=21000 N/mm² e del momento di inerzia Ix= 227813 cm4, a questo punto si può calcolare l’abbassamento massimo Vmax= qel4/8EIx. Si ottiene un Vmax= 0,66 cm. Essendo il rapporto tra luce e abbassamento massimo maggiore di 250 (come imposto da normativa) la sezione risulta verificata.

SOLAIO IN ACCIAIO
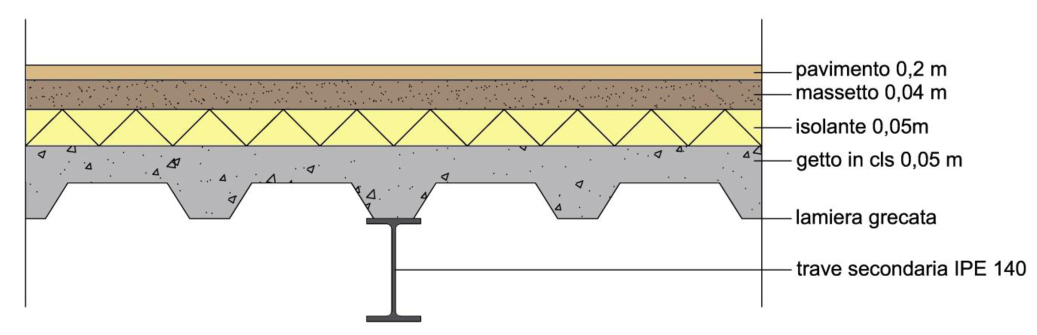
Analizzo il carico strutturale qs, il carico permanente qp e il carico accidentale qa.
Carico strutturale qs = 1,783 KN/ m²
Carico permanente qp = 2,635 KN/ m²
Carico accidentale qa = 2 KN/ m²
Dopo aver trovato i valori dei carichi qs, qp e qa e averli moltiplicati per i rispettivi coefficienti di sicurezza, si ottiene il carico qu e di conseguenza il momento massimo di una mensola che è pari a M= ql²/2, ovvero M=166,87 KNm.

Ottenuto il momento massimo scelgo la classe dell’acciaio e la sua tensione caratteristica di snervamento.Si trova ora il modulo di resistenza a flessione minimo Wx,min= Mmax/fd ottenendo Wx,min= 745,58 cm³; quindi si sceglie un profilo che abbia il modulo di resistenza superiore al valore minimo, ovvero una IPE 360 con Wx= 903,6 cm³, Ix= 16270 cm4 e peso= 0,571 KN/m.
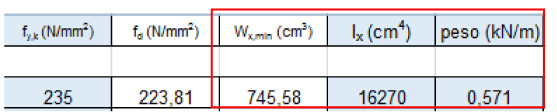
Dopo aver dimensionato la sezione, bisogna effettuare la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce e questo calcolo si effettua allo SLE (Stato Limite di Esercizio).
I carichi vengono ricombinati seguendo la combinazione frequente e viene aggiunto il peso proprio della trave:
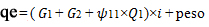
A questo punto si può calcolare l’abbassamento massimo Vmax= qel4/8EIx. Si ottiene un Vmax= 0,659 cm. Essendo il rapporto tra luce e abbassamento massimo maggiore di 250 (come imposto da normativa) la sezione risulta verificata.

SOLAIO IN LEGNO
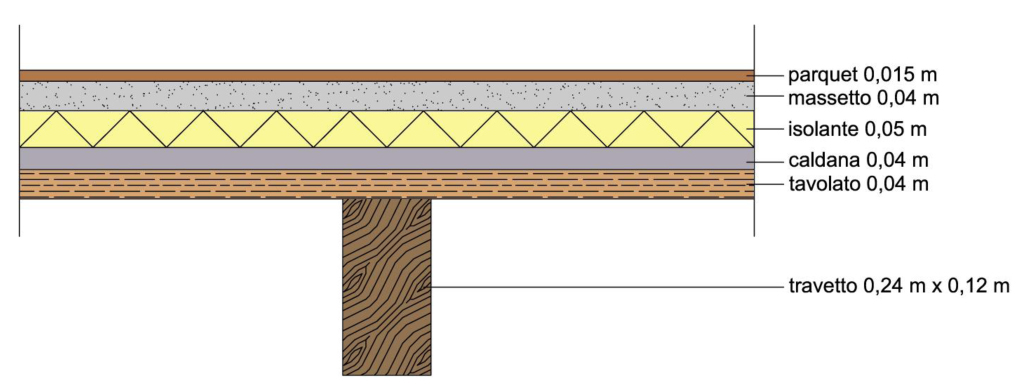
Analizzo il carico strutturale qs, il carico permanente qp e il carico accidentale qa.
Carico strutturale qs = 0,413 KN/m²
Carico permanente qp = 2,635 KN/m²
Carico accidentale qa = 2 KN/m²
Dopo aver trovato i valori dei carichi qs, qp e qa e averli moltiplicati per i rispettivi coefficienti di sicurezza, si ottiene il carico qu e di conseguenza il momento massimo di una mensola che è pari a M= ql²/2, ovvero M=134,80 KNm.

A questo punto si sceglie un legno GL 24h con resistenza a flessione fmk= 24 Mpa. Scelto come materiale il legno massiccio si ottiene un Kmod= 0,60 e un coefficiente γm= 1,50, si stabilisce una base b= 30 cm trovando un’altezza ingegnerizzata pari a H= 55 cm.

Dopo aver dimensionato la sezione, bisogna effettuare la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce e questo calcolo si effettua allo SLE (Stato Limite di Esercizio).
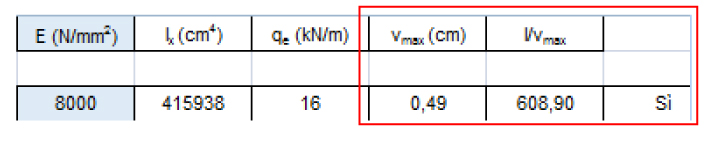
I carichi vengono ricombinati seguendo la combinazione frequente e il peso proprio della trave non viene considerato in quanto il legno è un materiale leggero:
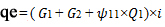
Ora si può calcolare l’abbassamento massimo Vmax= qel4/8EIx. Si ottiene un Vmax= 0,49 cm. Essendo il rapporto tra luce e abbassamento massimo maggiore di 250 (come imposto da normativa) la sezione risulta verificata.
Commenti recenti