Ho fatto un confronto tra l'analisi della curvatura fatta in Rhino e quella fatta in Inventor, verificando quella Gaussiana; per renderle visibili ho dovuto fare l'analisi della superficie in un intervallo che va da un valore minimo di (- 0,0001) ad uno massimo di (0,0001). Le scale cromatiche sono diverse ma il risultato è identico. Come prossimo passo vorrei verificare a mano uno di questi valori per capire meglio come lavorare sugli intervalli, per poi ripetere il procedimento sclando la superficie e rendendola più piccola.
Le immagini sono prese da Inventor (sopra) e Rhino (sotto):
Mi sono accorto solo ora dei tuoi post sul blog.. era un po' che nn lo aprivo, in ogni caso se hai bisogno di qualcosa chiedi pure, in ogni caso seguirò gli sviluppi quando ne posterai.. sono curiosissimo di cosa verrà fuori.
Ho utilizzato Autocad per provare dare una forma tridimnsionale ad una curva, sia con sezione costante, sia con sezione variabile.
Il primo comando che ho utilizzato è stato il "LOFT", che unisce tramite "rigata" o "levigata adattata" due o più sezioni trasversali. L'impedimento è il loft viene eseguito semre su traiettoria retta, a meno di alcune possibili modifiche, ma non si può chiedere di unire due sezioni seguendo un percorso (ossia la curva, disegnata o con la "polilinea" o con la "spline"). Per far si che i risultato finale seguisse effettivamente la curva disegnata, ho diviso quest'ultima in più parti ed ho copiato la sezione che volevo dare all'oggetto tridimensionale sui diversi punti per poi unirli traite "levigata adattata".
Il secondo comando che ho utilizzato, lo "Sweep", è molto più veloce e preciso, ma ha la limitazione di non consentire un una sezione variabile. In pratica, disegnata una sezione iniziale, si comanda di estruderla secondo un percorso, in questo caso la curva:
Grazie all'unione dei comandi "LOFT" e "SWEEP" in breve tempo sono riuscita a rappresentare la superficie di cui avevo eseguito l'analisi della curvatura gaussiana ipotizzandone una tessitura (ovviamente in modo arbitrario) che riprendesse queste curve:
Le tre linee più scure sono delle facce 3D di cui non esiste, e non sono riuscita a creare, una traccia continua, per cui era impossibile eseguire lo SWEEP. Di conseguenza ho creato i solidi (con LOFT) come segue:
Le linee trasversali sono curve, per cui, disegnata la sezone, eseguito lo SWEEP:
Da cui:
Ho poi importato il risultato finale in "3D Studio Max" ed ho verificato che tutti i solii creati venissero riconosciuti come superfici a cui sarebbe possibile applicare dei materiali per un eventuale render.
ho visto che hai cercato di fare una forma libera partendo da più sezioni "sweppate" su un solo binario, se l'obiettivo rimane quello di creare una forma arbitraria potresti provare a fare uno sweep di un'unica sezione su due binari diversi..
tipo cose del genere..
anche se il controllo di tal superfice è un po' "sfuggente"..
Infatti Rhino, che per me è ancora molto da scoprire, mi sembra più adatto a certe cose. Comunque l'importante ora era verificare che si potesero rappresentare diverse forme o sezioni, quindi mi hai dato un ottimo consglio...la necessità o meno di controllarle è un problema che mi porrò a breve.
Ho provato a fare le sweep da Rhino, sia con un solo binario e diverse sezioni:
Sia, come suggerito da Daniele, con una sola sezione e due binari (le curve disegnate nell'immagine sopra accanto alla superficie), ottenendo risultati interessanti:
come modellatore di superfici rhino è tra i programmi più efficienti e di semplice utilizzo, ti consiglio di sfruttarlo molto! l'ho sempre trovato molto intuitivo
Il lavoro procede, grazie per l'interesse, ora serve solo l'abilitazione! ma arriverà a breve..
Ho utilizzato rhino per altre prove di estrusione. In ognuno di questi esempi ho disegnato un unico binario, coincidente con l'asse centrale di una ipotetica trave;
Nella seguente immagine ho eseguito lo Sweep disegnando le sezioni iniziale, finale e di mezzeria, quest'ultima alta il doppio delle altre:
Le altre prove sono state eseguite sempre con il comando Sweep, ma disegnando solo la sezione iniziale e quella finale:
Ho generato una superficie in Rhino utlizzando il loft e la modellazione tramite punti di controllo. L'ho poi salvata in DWG ed importata in Autocad; il file di disegno conteneva, non una superficie, ma le linee tramite cui l'avevo generata e modellata:
A questo punto ho eseguito lo Sweep lungo queste curve disegnando una sezione rettangolare 80x30, costante, considerando le linee come assi centrali e le sezioni sempre ad esse perpendicolari:
Il 3D di Autocad lavora con i solidi tramite "addizioni" o "sottrazioni"; per vedere cosa succedesse alle intersezioni di questo sistema di travi, ho sottratto alle "longitudinali" le "trasversali", e viceversa, rilevando anche delle imperfezioni:
Nonostante queste imprecisioni ho importato il modello in 3Ds Max per fare una prova di resa con i materiali. Ho immaginato dapprima una tessitura in cemento, ed in secondo luogo una tessitura mista tra pannelli in plastica e struttura in metallo:
L'intento di questa prova era di cominciare a prendere confidenza con le linee coordinate, a partire dall'analisi di una superficie semplice. Sulla sfera le linee coordinate rappresentano i meridiani ed i paralleli, per cui quello che ho fatto è stato disegnare una sfera nello spazio tridimensionale di autocad, con raggio 2m e centro coincidente con l'origine del sistema di riferimento cartesiano; su questa sfera ho poi disegnato alcuni meridiani e paralleli calcolati nel seguente modo:
Ho estruso degli elementi a sezione rettangolari lungo queste linee coordnate:
Su questa superficie ho eseguito l'analisi della curvatura.
Gaussiana:
Mediana:
Mediana con un differente intervallo:
Infine ho renderizzato l'immagine assegnando dversi materiali:
Allora, ho trovato questo comando che penso potrà esserci molto utile. Si chiama "Proietta", funziona così: disegno una superficie nello spazio e disegno un curva sul piano orizzontale in corrizpondenza di questa superfcie; questo comando proietta un qualsiasi tipo di curva su una superficie qualsiasi adattando la curva alla forma di quest'ultima. Facendo un esempio pratico, ho disegnato una spirale e sopra di essa una sfera, poi ho chiesto a Rhino di proiettare la spirale sulla sfera e questo è il risultato:
Dove si vede in rosso la spirale piana, in nero la proiezione sulla sfera, ed in giallo le linee di costruzione della sfera. Per verificare che queste linee venissero lette correttamente ho importat il file in autocad ed ho ripetuto il processo di estrusione, fino ad arrivare ad un modello tridimensionale che ho potuto renderizzare in 3Dstudio:
Ho modellato una superficie seguendo un percorso che era meglio orientato. In particolare questa prova vuole essere da una parte una sintesi, o meglio, una via d'utilizzo delle nozioni fin qui apprese a livello di modellazione di software; dall'altra una prima interazione con il programma di calcolo meccanico. C'è quindi un obiettivo aggiunto, che ha comportato diversi problemi.
Il primo passo è stata la creazione della superficie in Rhino. Questa è stata generata e modellata a partire da un rattangolo di dimensioni 25x15 m immaginato orientato secondo gli assi x ed y, per poi essere suddivisa in mesh triangolari facilmente leggibili da SAP. Successivamente ho disegnato sulla proiezione a terra un graticcio 1x1 e l'ho poi proiettato (tramite il comando "proietta") sulla superficie:
Nella figura si vedono le linee in rosso che sono le linee proiettate sulla superficie, e quelle in viola che appartengono al piano xy e definiscono la figura di partenza.
Come prima cosa ho provato ad importare la superficie in SAP per verficare che venisse letta correttamente:
Come si vede nella figura sottostante, selezionando tutte le linee sembra non ci siano imprecisioni:
Questo passaggio, grazie ad una verisone più aggiornata di SAP, non ha creato problemi. Il passaggio ostico è stata l'importazione del solo graticcio.
Salvando il file dxf da Rhino, Sap non leggeva nessuna linea. Facendo diversi tentativi di capirne il motivo ho notato che le linee proiettate, ovvero quelle che formavano il graticcio, venivano lette male sia in Rino che in Autocad, per cui risultava impossibile anche eseguire lo sweep. Lavorando su Autocad ho capito che Sap legge solo le polilinee3D, mentre la modellazione fatta fino ad ora si basava su spline e polilinee2D. Sono sicura che esiste un modo per convertire un elemento nell'altro, ma è più difficile da trovare di quanto credessi; quello che ho fatto è stato ricalcare in Autocad il graticcio con le polilinee3D, per poi importarlo in SAP ed avre la possibilità di esegurne uno sweep:
Come si può vedere a questo punto l'importazione non da problemi, almeno apparentemente.
Ho risolto molti problemi, sebbene ancora non tutti, riguardo l'importazione in SAP. Il metodo che avevo usato risultava lungo (poichè dovevo ricalcare il graticcio in autocad) e poco utile, poichè non venivano riconosciuti i nodi all'intersezione delle curve.
Per migliorare questi aspetti sono partita da Rhino.
Il graticcio che ho disegnato tramite il comando "Proietta" non riconosceva i nodi poichè si tratta di polilinee continue:
Ho provato ad aggiungere i punti, con il comando "Punto" di Rhino nelle intersezioni, ma SAP non è in grado di leggerli. Per cui ho pensato che l'unico modo per far riconoscere i nodi a SAP sarebbe stato quello di spezzare le curve nei punti di intersezone. Il metodo più veloce che ho trovato è il seguente: Seleziono tutte le curve e uso il comando "Intersezione":
Questo comando genera solo punti laddove riconosce delle intersezoni, nel caso non le riconosca è possibile aggiungerli manualmente. Poi ho usato il comando "Suddividi", dicendo che tutte le curve erano gli oggetti che volevo suddividere, mentre i punti erano gli oggetti di taglio:
In questo modo Sap è in grado di riconoscere con precisione tutti i nodi. Infine il passo fondamentale è stato quello di NON usare un file dxf, ma di salvare il disegno in formato IGES (.igs) che, a quanto pare, è di più facile lettura. A questo punto il passaggio tra Rhino e SAP è immediato:
Ho selezionato il file IGES da importare, in questo caso SAP non ti chiede quale layer vuoi utilizzare, ma importa tutti i layer del disegno, per cui è bene pulire il file direttamete da Rhino:
Ci sono però ancora dei problemi. SAP crea dei punti di discontinuità:
Ci sono dei comandi di Rhino che mi possono aiutare a semplificare le curve, lavorando sulle tolleranze si dovrebbe riuscire a ridurre il numero di linee ed a far leggere il file senza più errori.
Era un problema di facile soluzione. Quando si importa il file in SAP bisogna stare attenti alle unità di misura:
Lo stesso File non presenta più problemi se importato con le unità di misura giuste. Inoltre ho provato a ridurre il numero di Frames, prima da SAP utilizzando "Merge Joints": la tolleranza più alta che non distorce la geometria è di 0,001 e non ha effetto sul numero di Frames (3942). Così ho lavorato su Rhino con il comando "Semplifica Curve" che ha ridotto il numero a 3173. Ripetendo più volte il comando si arriva ad una approssimazione massima di 3168 Frames.
Per verificare l'attendibilità del metodo ho ripetuto tutti i passaggi per un secondo graticcio la cui tessitura è inclinata a 45°: Da Rhino ho utilizzato, in ordine, i comandi : INTERSEZIONE; SUDDIVIDI; SEMPLIFICA (Due volte) SALVA IGES.
Poi in SAP ho cambiato l'unità di misura del disegno in KN, m, C, ed ho importato il File senza nessun problema.
Ho provato a realizzare un modello utilizzando le curve geodetiche. Ho lavorato solo su Rhino e 3Dstudio; come prima cosa ho generato e modellto la superficie tramite i comandi di "Loft" e "Punti di Controllo"
Ho poi diviso le curve generatrici in 40 pezzi (misuravano cirvca 40 metri) ed ho unito i punti tramite il comando "CurvaGeodetica", sia passando per la curva centrale (Rosso) sia andando direttamente da parte a parte (Verde):
Ho deciso di provare a renderizzae un modello estrudendo le geodetiche in Rosso ed aggiungendo due curve intermedie lungo il lato lungo (in blu).
Sono linee tracciate in modo pressochè casuale, nel senso che immagno si possano disegnare queste curve con un criterio che tenga in considerazione le conseguenze meccaniche che vi sarebbero nel caso in cui una curva geodetica rappresentasse una trave, o un elemento struttrale. Di fatto questo passaggio logico mi sfugge, come mi sfugge, non avendo ancora approfondito l'argomento, il significato reale di queste curve; ad ogni modo forse questo esercizio, agli occhi dei più esperti, può aiutare a capire se si tratta di un approfondimento sarebbe o meno necessario fare.
Ho provato a fare l'analisi del graticcio con Sap, ma ho molti dubbi sulla correttezza del risultato. Il procedimento è stato il seguente:
Assegnare i vincoli a terra lungo tutto il perimetro (incastri); Assegnare una sezione (uguale per tutti) ad ogni Frame; Assegnare un carico distribuito a tutta la struttura; Avviare l'analisi escludendo l'analisi modale. Ho lasciato che SAP calcolasse in automatico il peso proprio della struttura tramite le caratteristiche di deafult del materiale, ecco uno schema riassuntivo:
Ecco le immagini relative all'analisi di: Momento:
Taglio:
e Normale:
Ed il grafico della deformata (in grigio):
La deformata mi sembra corretta, quindi in teoria dovrebbero essere corretti anche i grafici delle sollecitazioni. Poichè la struttura è molto grande ho scalato i grafici a seconda delle necessità perchè risultassero visibili, per cui possono sembrare esageratamente accentuati, ma spero che salmeno si riescano a leggere. Ad ogni modo ho approfondito il comportamento di diverse curve per verificarne il funzionamento.
La prima, una della curve centrali più sollecitate:
Di cui riporto i grafici del taglio:
e del momento:
Anch'essi scalati a seconda delle necessità. In generale il mio dubbio è questo: ogni nodo interno, perchè il graticcio abbia senso, deve essere un incastro, ma io non ho assegnato nulla ai nodi sapendo che SAP li considera incastri di default. Quello che mi aspetto però è che in quei punti il momento non sia nullo o che comunque si noti la discontinuità. La "scalettatura" del grafico del momento sopra riportato può essere riconducibile a questo ragionamento, ma non ne sono convinta, specialmente sapendo cosa è venuto fuori dall'altra analisi...:
La seconda curva è stata presa sul lato lungo:
Anche qui abbiamo i grafici del taglio:
e del momento:
Le linee verticali sono i valori, nei nodi, di taglio e momento delle aste ortogonali (sembrano enormi, ma si tratta del problama di scala legato alla visibilità,, ho controllato i valori e sembrano "umani"). Credo si vedano in questi grafici e non nei precedenti semplicemente per delle impostazioni di visulaizzazione di SAP di strutture. Comunque il problema qui, detto in tutta sincerità, è che questo grafico mi sembra tanto strano e non so se lo capisco tanto bene da poter capire se è giusto o sbagliato.
Come ultima cosa ho preso una curva sul bordo:
Sia il grafico del taglio:
che quello del momento:
(accentuati) mi sembrano evidentemente corretti. I dubbi rimangono sui nodi centrali.
Ho eseguito l'analisi, come precedentemente descritta, sulla stessa superficie, prima considerando un secondo graticcio, e poi considerando la superficie stessa una soletta in c.a.
SECONDO GRATICCIO:
Riporto la configurazione iniziale:
ed i grafici delle sollecitazioni di Momento:
Taglio:
e Normale:
Ed infine la deformata:
SOLETTA in C.A.
L'importazione della superficie come shell (tramite salvataggio in file dwx) non ha riportato problemi:
Ho vincolato l'intero perimetro e cominciato l'analsi.
Ho riportato tutti i valori massimi dei risultati che mi sono comparsi, senza capirne però la vera natura. In attesa di studiare più approfonditamente il concetto di shel e di membrana, allego i grafici dei suddetti risultati:
Ho provato a studiare una superficie di cui conoscevo l'equazione per cercare di disegnarvi sopra le linee di curvatura ed utilizzarle poi per il calcolo strutturale. La superficie in questione è un paraboloide ellittico della forma z = x^2 + y^2, ho svolto tutti i calcoli del caso a mano e li ho rassunti in questa pagina:
A questo punto sono passata a Rhino. Per disegnare il paraboloide ho utilizzato il comando "Paraboloide".
Il caso preso in considerazione è quello di un paraboloide generato dalla rotazione di una parabola z = x^2 intorno all'asse delle z, per cui ho individuato il vertice (0,0) ed il fuoco (0,1), ed immesso i dati.
Sono poi passata allo script. Le famiglie di curve individuate sono le proiezioni delle linee di curvatura sul piano xy, per cui ho riportato le equazioni nello script prima delle circonferenze:
E poi delle rette:
Ottenedno il seguente risultato:
A questo punto ho utlizzato il comando "Proietta" per ottenere la proiezione di cueste curve sulla superficie:
Disegnandovi, appunto, le linee di curvatura. Ho fatto poi un'ulteriore considerazione:
per prima cosa tengo a precisare che sono assolutamente certa di questo risultato poichè l'ho confrontato anche con gli esercizi svolti del testo "Problemi di geometria differenziale";
Detto ciò, essendoci spesso interrogate sulla natura dell' "analisi zebra" di rhino, ho svolto l'analisi su questa superficie. Una volta svolta ci viene data la possibilità di scegliere se visualizzare le linee zebra verticalmente o orizzontalmente, in direzioni, quindi, tra loro perpendicolari. Questo ha fatto sorgere il dubbio che le linee zebra altro non fossero che la rappresentazione grafica delle due famiglie di linee di curvatura. Ma svolta l'analisi del caso, mentre la rappresentazione della famiglia di linee verticali sembrava potesse confermare questa teoria:
Quella nella direzione orizzontale ha cancellato ogni dubbio:
Quindi le linee zebra NON sono le linee di curvatura, il che spiegherebbe anche l'assenza di un apposito comando di Rhino che fosse in grado di disegnarle, come accade infatti con le curve geodetiche.
Come ultima cosa, prima di passare all'analisi strutturale, ho provato ad utilizzare il linguaggio dello script per generare una superficie apparentemente più complessa sulla quale vorrei svolgere i medesimi calcoli: z = sinx siny:
Ho eseguito il calcolo in SAP del paraboloide ellittico. Ho provato anche a fare l'analisi considerandolo una shell, ma non potendone capire i risultati credo sia più importante adesso cercare di vedere quali passaggio ho fatto per calcolare il graticcio e vedere se il procedimento è corretto o se non considero alcuni elementi
Ho eliminato le aste del verice perchè so che il sistema funziona ugualemente, e mi semravano troppo ravvicinate; tuttavia non credo sia una scelta dovuta.
L'impostazione dell'analisi è la seguente:
VINCOLI a terra: CERNIERE
NODI: INCASTRI (non ho assegnato nulla in particolare ai nodi perchè SAP dovrebbe riconoscerli come incastri di default)
CARICHI: 5kN distribuito + peso proprio della struttura
MATERIALE: ACCIAIO con sezioni Rettangolari 10x15cm di spessore 6,5 mm
A questo punto avvio l'analisi. I risultati che cerco, in questo caso, sono i valori massimi della normale (Axial Force):
Del taglio (shear 2-2):
e del Momento (moment 3-3):
Inoltre posso guardare la deformata per verificare che sia consona alla distribuzione dei carichi:
Ho assegnato stessi carichi, stesso materiale e stessa sezione. Gli elementi strutturali corrispondono a meridiani e paralleli, quindi alle linee coordinate; inoltre ogni direzione è una direzione principale, quindi si può dire che corrispondano anche alle linee di curvatura; nel caso dei meridiani, inoltre, essi rappresentano le curve geodetiche che uniscono i punti appartenenti alla circonferenza di base con il vertice. I risultati sono i seguenti:
Ho rifatto il calcolo dei graticci (post #22 e #23). Avevo incastrato la struttura ed avevo assegnato una sezione troppo grande per un reticolo così fitto. I termini per l'analisi, in entrambi i casi, sono i seguenti:
VINCOLI: CERNIERE
MATERIALE: ACCIAIO con sezione rettangolare 20x10 cm di spessore 4 mm
CARICHI: 5kN distribuito + peso proprio
NODI: INCASTRI (assegnati in automatico da SAP)
Ho quindi analizzato i due casi.
1) GRATICCIO (1x1 m), con inclinazione delle aste a 90°.
Momento:
Taglio:
Normale:
Deformata:
2) GRATICCIO (1x1 m), con inclinazione delle aste a 45°.
Oggi ho installato la versione 8.0 di Mathematica ed ho cominciato a vedere come funziona perchè sulle forme parametriche è possibile calcolare le equazioni delle due famiglie di linee di curvatura, ma fare questo calcolo a mano è possibile solo su superfici descritte da un'equazione molto semplice, e comunque, arrivati ad un certo punto del calcolo, le cose si complicano inevitabilmente.
Stavo cercando di trovare le linee di curvatura della superficie z = Sin(x)Sin(y) che ho sviluppato con lo script e pubblicato nel post #24; in Mathematica viene rappresentata così:
Svolgendo i calcoli si arriva ad avere un'eqazione di questa forma:
Da qui in poi gestire il calcolo a meno diventa davvero complicato. Bisogna svolgere un sistema per trovare i rispettivi valori di A e B, ma la semplificazione migliore, ad ora, è la seguente:
Che va sostituto all'equazione in B. Al di là di questo esempio credo comunque sia utile imparare ad utilizzare il programma, per non essere bloccata dal calcolo nel caso si scegliesse di studiare una forma parametrica.
Mi piacerebbe portare due metaprogetti, una geometria gestibile a livello parametrico ed una geometria libera. Credo sia il modo migliore di rappresentare questa ricerca, per diversi motivi: il primo è che i due approcci, visti insieme, mettono in evidenza uno i limiti dell'altro e risultano meglio comprensibili; il secondo è che tutto il lavoro fatto rende possibile la gestione dell'uno e dell'altro tipo di forma, e limitarsi ad approfondirne una sola mi sembra non del tutto esaustivo. A questo proposito ho sviluppato due ipotesi sulle queli si potrebbe lavorare:
FORMA PARAMETRICA. Generta tramite il seguente script:
Ovvero:
Che risulta fin troppo semplice forse, ma la modifica dell'altezza tramite lo script è più difficoltosa di quanto mi aspettassi. Non so se dettato dalla stanchezza, ma io c'ho trovato un certo fascino, quindi ho ipotizzato una tessitura:
Vista in tre dimensioni:
Non sono andata oltre su questo esempio perchè ho diverse riserve riguardo la geometria.
FORMA LIBERA. Generata a partire da quattro curve (in rosso nella figura) mediante il comando Loft, e riferendomi ad una base composta di due circonferenze (in nero) di 80 e 40 metri di diametro:
Nel processo di modellazione tramite punti di controllo ho anche deciso di inserire delle bucature (cerchi in blu nella figura), ed ho ottenuto il seguente risultato:
In questo caso sono andata avanti perchè, sinceramente, questa forma mi piace. Ho provato quindi ad esportala in SAP2000; la prima divisione in mesh è stata effettuata con una densità pari ad 1.0:
Ma era impossibile lavrarci in SAP, evidentemente pesa troppo ed il programma gira lentissimo. Allora ho creato una seconda mesh con densità 0.7, sulla quale è stato possibile lavorare:
Prima di passare a SAP ho tentato di generare una tessitura. Dapprima ho utilizzato un sistema di riferimento polare (con origine coincidente con il centro della circonferenza più piccola) ed ho generato una grid shell di linee coordinate:
Esteticamente questa grid-shell non ha grande valore ed andrebbe disegnata con più accuratezza, ma ho comunque provato a fare un'analisi per rendermi conto di quanto la geometria fosse getibile.
Come ultima cosa, prima di passare al SAP, ho provato a generare una grid-shell composta di curve geodetiche e, con mia grande sorpresa, il comando su questa superficie non funziona. Mi spiego meglio: seguendo lo stesso procedimento di sempre ho suddiviso i limiti interni ed esterni della superficie in 60 parti ed ho poi provato a generare le geodetiche da punto a punto, ma il risultato è stato il seguente:
Probabilmente è una geometria troppo complessa anche per Rhino. Questo è un aspetto che vorrei capire meglio, appena possibile cercherò di analizzarlo.
Vediamo le analisi strutturali in SAP, premetto che ad entrambi ho assegnato un carico distribuito pari a 4 kN e non ho considerato il contributo del peso proprio.
GRID-SHELL. Il File viene letto senza errori:
Il materiale è acciaio, sezione scatolare di altezza 15 cm, larghezza 10 cm e spessore 6,5 mm. Riporto solo il grafico della sollecitazione normale poichè sia la deformazione sia i valori di taglio e momento sono trascurabili. Riguardo lo sforzo assiale, invece, il valore massimo è di 1475 kN (il cerchio più grande), ma i punti di "picco" sono locali e si potrebbe intervenire sulla geometria per correggerli:
SHELL. Ho importato la shell e verificato che venissero letti tutti gli elementi:
A questo punto ho asegnato il materiale ed il carico. Stavolta ho studiato prima di fare l'analisi per capire bene quali parametri andare a toccare: ho scelto come carico Area Loads e poi Uniform (Shell) che viene applicato alla superficie mediana della shell (che coincide con la superficie importata); sono poi andata a definire la sezione del'area tramite questa finestra:
Ho importato il file come "Shell", per cui in Type potevo scegliere solo tra le opzoni Thin e Thick, ho scelto Thin nonostante la tipologia Thick sia più accurata. La scelta del tipo Thin, però, è consgliabile quando si analizzano mesh distorte o quando si è certi che la deformazione a taglio sia trascurabile, ed essendo la deformazione a taglio importante solo quando lo spessore dell'area è più di 1/5 o 1/10 della luce, ho reputato Thin la scelta migliore. Ho impostato lo spessore (thickness) di 20 cm; questo valore, se ho capito bene, verrà utilizzato per caclolare la rigidezza della membrana (membrane) e la rigidezza torsionale (Bending), ed è uso comune stabilire lo spessore della membrana ed utilizzare quello stesso valore nella voce Bending. A questo punto ho avviato l'analisi, vediamo la deformata:
In cui si può notare che una parte della geometria si deforma troppo rispetto al resto.
Sempre se ho capito bene, il risultato che devo andare a guardare è Fmax, che fa parte delle Resultant Forces, anche dette Shear Element Internal Forces, da cui deduco che Fmax sia il valore massimo dello sforzo di membrana, di cui vengono rappresentati i valori medi mediante lo spettro di colori generato da SAP:
Non so bene quali siano i limiti entro i qual è ragionevole pensare ad un dimensionamento, ma i valori per ora mi sembrano essere molto elevati.
Per concludere, ho provato a renderizzare questa geometria per verificarne l'effetto visivo:
Nel Post #29 avevo individuato almeno tre punti della forma libera in cui le sollecitazioni avevano valori estremamente più alti della media. Ho quindi provato a correggere quei punti variandone la geometria. Ho fatto diversi tentativi e li ho analizzati su SAP come shell, ottenendo i seguenti risultati:
La modifica numero 3 ha dei valori degli sforzi gestibili, di seguito riporto i grafici relativi ad Fmax:
Ed Smax:
Da queste immagini si capisce che i valori di massimo e di minimo sono locali (potrebbero essere considerati puntali), mentre mediamente gli sforzi sono molto più bassi.
Ho preso per buona questa gemetria ed ho ipotizzato una GRID-Shell che vi si adattasse:
Le curve in bianco sono 80, ed hanno origine nel centro della circonferenza piccola (tramite la quale ho costruito la geometria). Le curve in blu, invece, sono curve geodetiche. Sempre nel post #29 avevo evidenziato un problema di Rhino, ovvero che non riusciva a disegnare le curve geodetiche su questa forma: questo è vero in senso trasversale, mentre longitudinalmente le curve vengono disegnate senza problemi. Per costruire questa GRID-Shell, quindi, ho suddiviso in 10 parti alcune delle curve in bianco (che sono a tutti gli effetti linee coordinate), e le ho collegate tramite il comando "CurvaGeodetica". A questo punto ho condotto l'analisi in SAP: ho utilizzato scatolari in acciaio, variandone la sezione:
Ho scelto poi di utilizzare una sezione 20x40. Come si può vedere con una sezione più grande (25x50) i valori delle sollecitazioni si abbassavano ulteriormente, tuttavia la differenza con le sollecitazioni della prova precedente mi è sembrata troppo piccola in relazione all'aumento del materiale, ed ho quindi preferito considerare migliore la sezione 20x40. Riporto i grafci dello Sforzo Assiale:
Del Taglio:
E del Momento:
Anche in questo caso i valori medi delle sollecitazioni sono molto più bassi di quelli massimi o minimi. Si può quindi procedere individuando i punti critici e correggendone la geometria. Nel frattempo ho fatto una prova di render anche per la GRID-Shell:
è un po' che non commento il tuo blog, il tuo lavoro va avanti è vedo che hai raggiunto buoni risultati, sei partita con un concetto molto più astratto del mio, e sei arrivata un po' al mio punto di partenza... mi sembra bello vedere quanto lavoro può essere fatto prima di pansare ad una forma anche se astratta.. ti faccio i miei complimenti.. soprattutto per averlo descritto step by step.
la forma in se comincia ad essere molto interessante a mio avviso... se fosse tutta una superficie unica e liscia trattata come un fazzolettone sarebbe veramente interessante.. ma questo è un mio giudizio personale... esoprattutto porta non poche complicazioni strutturali... per quanto riguarda invece le correzioni geometriche per ottenere sforzi sufficientemente accettabili nel mio blog c'è molto materiale. io mi sono scontrato con delle trazioni tremende e la geometria della mia forma ha dovuto compensare queste grandissime trazioni. se hai domande a riguardo sono tutto orecchie.
continuo a seguire con molto interesse il tuo blog.. buon lavoro.
Mi fa piacere sapere che continui a seguire il blog, ti ringrazio per l'incoraggiamento!
Per quanto riguarda la forma libera stiamo considerando sia il caso della shell, sia il caso della Grid-shell, ad ogni modo mi confronterò a breve con le dovute complicazioni ed il tuo blog tornerà ad essermi utile come sempre.
Grazie anche per la disponibilità, in caso avessi dei dubbi ti contatterò, spero che il lavoro ti vada bene, a presto
(Per Daniele: appena avrò conferma ti scriverò la data!)
Intanto ho modificato lo script della forma parametrica che avevamo scelto per adattarla ad una stanza rettangolare, immaginandola quindi come un oggetto ornamentale. Non ho esguito alcun calcolo perchè volevo essere prima certa dell'effetto, questo è il render:
(Ho fatto molte prove con diversi tipi di luci)
Adesso vorrei riuscire ad utilizzare questa forma, con le dovute modifiche, ad una scala un pò più grande, o comunque in condizioni in cui risulti portante. Per quanto riguarda la forma libera invece ho risolto il problema della fessurazione per i carichi verticali, ma ho dei dubbi circa il sisma di cui parleremo meglio domani.
la forma parametrica è bellissima. Prendi in considerazione che a dimensioni più grandi piena non resiste e sarebbe MERAVIGLIOSO se fosse nervata con le nervature dirette lungo le linee di curvatura.
Allora, cito testualmente quanto riportato dal testo Schaum a pagina 185:
"Teorema 9.9. Una direzione du:dv è una direzione principale in P se e solo se du e dv soddisfano la condizione:
(EM - LF) du2+ (EN - LG) dudv+ (FN - MG) dv2= 0
Si può dimostrare che in un punto non ombelicale questa equazone si fattorizza in due equazioni lineari della forma A du + B dv = 0 relativa alle due direzioni principlai, perpendicolari tra loro."
Questo teorema si rifersca a carte locali arbitrarie e non a casi particolari, per cui le direzioni principali sono sempre ortogonali. A mio avviso abbiamo male interpretato il significato di "du:dv". Infatti più di una volta viene scritto che le linee coordinate si dispongono ortogonalmente una in direzione du=0,dv=1 ed una in direzione dv=0,du=1, qundi la direzione non viene indicata con il rapporto du/dv anche perchè, nel caso delle linee coordinate, una delle due direzioni risulterebbe uguale ad un numero diviso zero, che è impossibile.
Sempre lo Schaum a pagina 186 dice:
"Teorema 9.14. La direzione du:dv in un punto di una carta locale rappresenta una direzione principale se e solo se per un opportuno scalare k, dN = Nudu + Nvdv e dx = xudu + xvdv soddisfano la relazione:
dN = - k dx
In questo caso k è la curvatura principalenella direzione du:dv.
La formula precedente, che caratterizza completamente le direzioni principali, viene detta formula di Rodrigues, e dovrebbe essere imparata a memoria."
Allego anche un'immagine che ho sempre dimenticato di postare di com'è diventata la forma libera a seguito di tutte le modifiche dovute al calcolo, ora dovrebbe funzionare:
Ho provato a calcolare le linee di curvatura del paraboloide ellittico. Ho rifatto i calcoli in Maple trovando i coeficienti fondamentali:
Poi sono passata a RhinoScript ed ho provato a disegnare una sola linea di curvatura come una successione di punti, il risultato è il seguente:
I punti seguono effettivamente la linea di curvatura. Quindi ho ripreso in mano il file Maple del "fungo" ed ho ricontrollato ogni passaggio utilizzato per calcolare i coefficienti fondamentali, che risultano:
Quindi sono tornata sullo script ed ho provato a disegnare le linee di curvatura, prima in una direzione e poi nell'altra:
Quelle che vengono fuori sono le linee coordinate, ma se questo procedimento è corretto non caisco perchè i coefficienti fondamentali F ed M non sono uguali a zero. Ho comunque costruito la grid-shell:
L'unica spiegazione possibile è che nel generare la successione di punti nello script abbia reso un parametro costante. Se così fosse queste sarebbero le linee coordinate, non per forza linee di curvatura.
Quelle erano linee coordinate. Questa dovrebbe essere la nuvola di punti che identifica le linee di curvatura, sto cercando di capire come isolare una sola direzione perchè in questo modo non riesco a ricostruirle con precisione:
Commenti
Fabiana Riparbelli
Mar, 05/07/2011 - 14:35
Collegamento permanente
Primi Passi
Come prima cosa riporto l'immagine della superficie discretizzata disegnata in Rhino seguendo lo stesso procedimento già spiegato nel Blog di Nardone.
Fabiana Riparbelli
Mar, 05/07/2011 - 15:24
Collegamento permanente
Analisi Curvatura Gaussiana
Ho fatto un confronto tra l'analisi della curvatura fatta in Rhino e quella fatta in Inventor, verificando quella Gaussiana; per renderle visibili ho dovuto fare l'analisi della superficie in un intervallo che va da un valore minimo di (- 0,0001) ad uno massimo di (0,0001). Le scale cromatiche sono diverse ma il risultato è identico. Come prossimo passo vorrei verificare a mano uno di questi valori per capire meglio come lavorare sugli intervalli, per poi ripetere il procedimento sclando la superficie e rendendola più piccola.
Le immagini sono prese da Inventor (sopra) e Rhino (sotto):
DanieleNardone
Mar, 20/09/2011 - 15:21
Collegamento permanente
Buon Lavoro!
Ciao Fabiana,
Mi sono accorto solo ora dei tuoi post sul blog.. era un po' che nn lo aprivo, in ogni caso se hai bisogno di qualcosa chiedi pure, in ogni caso seguirò gli sviluppi quando ne posterai.. sono curiosissimo di cosa verrà fuori.
Buon lavoro!
Daniele
Fabiana Riparbelli
Mer, 21/09/2011 - 22:19
Collegamento permanente
Ciao Daniele
Grazie per l'augurio!
Piano piano posterò tutto, le cose stanno prendendo una bella direzione...
In bocca al lupo per il lavoro, spero che le cose ti vadano bene, a presto!
Fabiana Riparbelli
Sab, 01/10/2011 - 12:11
Collegamento permanente
Prove di Estrusione
Ho utilizzato Autocad per provare dare una forma tridimnsionale ad una curva, sia con sezione costante, sia con sezione variabile.
Il primo comando che ho utilizzato è stato il "LOFT", che unisce tramite "rigata" o "levigata adattata" due o più sezioni trasversali. L'impedimento è il loft viene eseguito semre su traiettoria retta, a meno di alcune possibili modifiche, ma non si può chiedere di unire due sezioni seguendo un percorso (ossia la curva, disegnata o con la "polilinea" o con la "spline"). Per far si che i risultato finale seguisse effettivamente la curva disegnata, ho diviso quest'ultima in più parti ed ho copiato la sezione che volevo dare all'oggetto tridimensionale sui diversi punti per poi unirli traite "levigata adattata".
Fabiana Riparbelli
Sab, 01/10/2011 - 12:17
Collegamento permanente
Prove di Estrusione_2
Come secondo passo ho provato a generare questi solidi utilizzando diverse sezioni e sezioni non costanti:
Fabiana Riparbelli
Sab, 01/10/2011 - 12:36
Collegamento permanente
Loft e Sweep
Il secondo comando che ho utilizzato, lo "Sweep", è molto più veloce e preciso, ma ha la limitazione di non consentire un una sezione variabile. In pratica, disegnata una sezione iniziale, si comanda di estruderla secondo un percorso, in questo caso la curva:
Grazie all'unione dei comandi "LOFT" e "SWEEP" in breve tempo sono riuscita a rappresentare la superficie di cui avevo eseguito l'analisi della curvatura gaussiana ipotizzandone una tessitura (ovviamente in modo arbitrario) che riprendesse queste curve:
Le tre linee più scure sono delle facce 3D di cui non esiste, e non sono riuscita a creare, una traccia continua, per cui era impossibile eseguire lo SWEEP. Di conseguenza ho creato i solidi (con LOFT) come segue:
Le linee trasversali sono curve, per cui, disegnata la sezone, eseguito lo SWEEP:
Da cui:
Ho poi importato il risultato finale in "3D Studio Max" ed ho verificato che tutti i solii creati venissero riconosciuti come superfici a cui sarebbe possibile applicare dei materiali per un eventuale render.
DanieleNardone
Lun, 03/10/2011 - 22:14
Collegamento permanente
ho visto che hai cercato di
ho visto che hai cercato di fare una forma libera partendo da più sezioni "sweppate" su un solo binario, se l'obiettivo rimane quello di creare una forma arbitraria potresti provare a fare uno sweep di un'unica sezione su due binari diversi..
tipo cose del genere..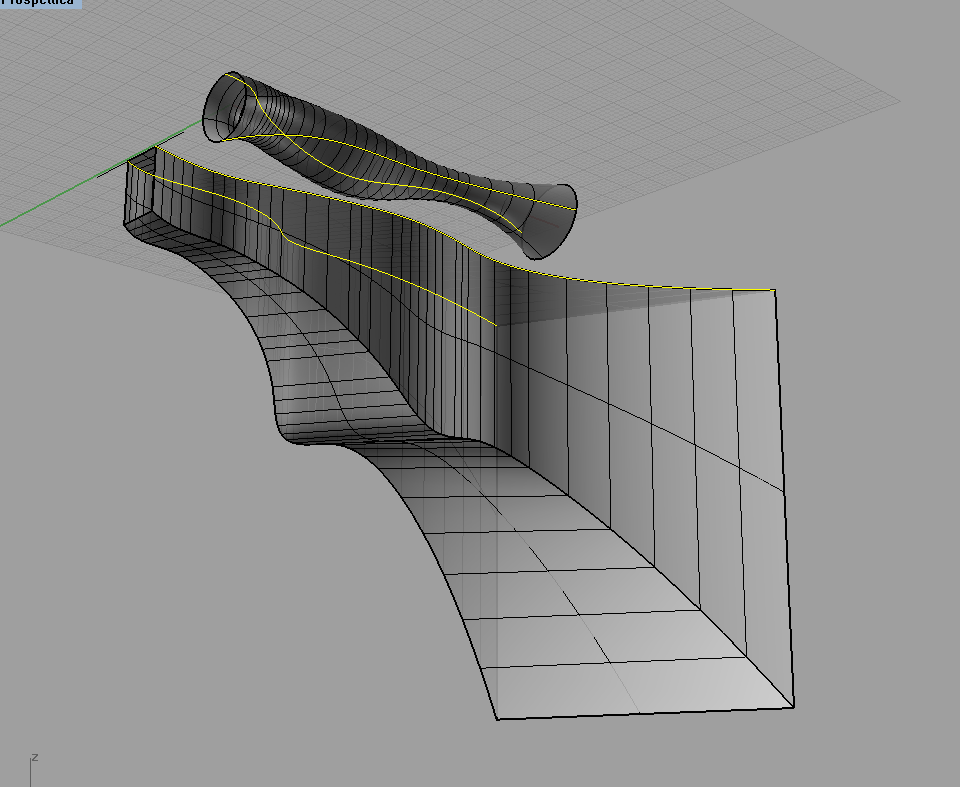
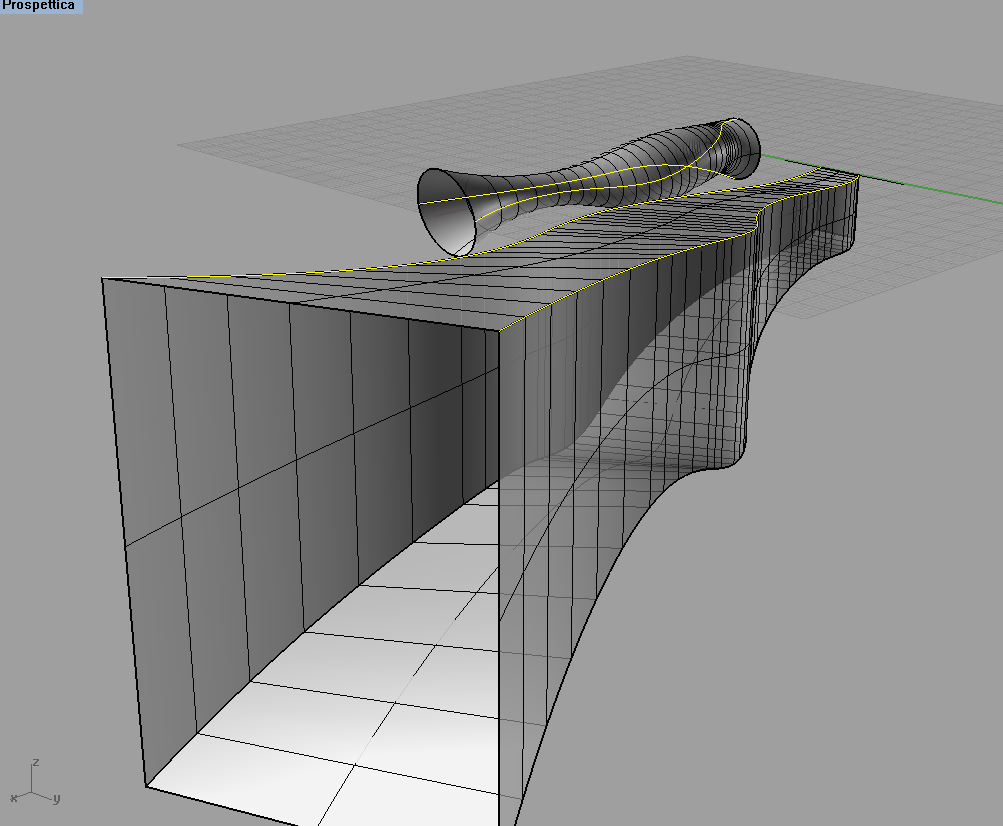
anche se il controllo di tal superfice è un po' "sfuggente"..
Fabiana Riparbelli
Mar, 04/10/2011 - 09:29
Collegamento permanente
è un ottimo consiglio
Infatti Rhino, che per me è ancora molto da scoprire, mi sembra più adatto a certe cose. Comunque l'importante ora era verificare che si potesero rappresentare diverse forme o sezioni, quindi mi hai dato un ottimo consglio...la necessità o meno di controllarle è un problema che mi porrò a breve.
Grazie mille! tutto bene con il lavoro?
a presto, Fabiana
Fabiana Riparbelli
Mar, 04/10/2011 - 09:48
Collegamento permanente
Sotto consiglio di Daniele
Ho provato a fare le sweep da Rhino, sia con un solo binario e diverse sezioni: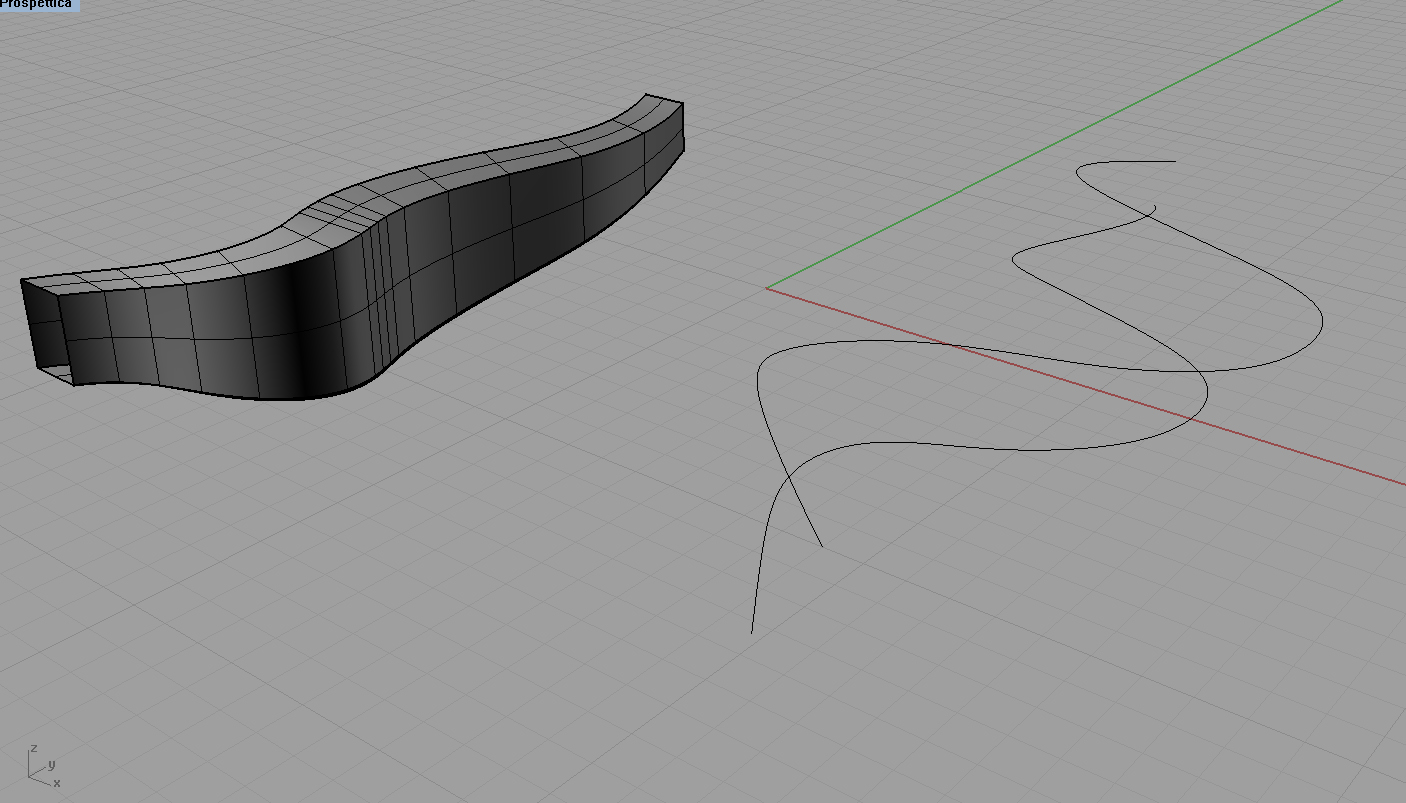
Sia, come suggerito da Daniele, con una sola sezione e due binari (le curve disegnate nell'immagine sopra accanto alla superficie), ottenendo risultati interessanti:
DanieleNardone
Mar, 04/10/2011 - 14:20
Collegamento permanente
felice di esserti utile
come modellatore di superfici rhino è tra i programmi più efficienti e di semplice utilizzo, ti consiglio di sfruttarlo molto! l'ho sempre trovato molto intuitivo
Il lavoro procede, grazie per l'interesse, ora serve solo l'abilitazione! ma arriverà a breve..
Buon lavoro
Daniele
Fabiana Riparbelli
Lun, 10/10/2011 - 20:47
Collegamento permanente
rhino
Fabiana Riparbelli
Mer, 12/10/2011 - 19:05
Collegamento permanente
Prova di rappresentazione
Fabiana Riparbelli
Gio, 10/11/2011 - 10:54
Collegamento permanente
Analisi curvatura da Rhino
Di questa superficie ho anche eseguito l'analisi della curvatura Gaussiana e Mediana.
Gaussiana:
Mediana:
Fabiana Riparbelli
Gio, 10/11/2011 - 11:18
Collegamento permanente
Prove su Sfera
L'intento di questa prova era di cominciare a prendere confidenza con le linee coordinate, a partire dall'analisi di una superficie semplice. Sulla sfera le linee coordinate rappresentano i meridiani ed i paralleli, per cui quello che ho fatto è stato disegnare una sfera nello spazio tridimensionale di autocad, con raggio 2m e centro coincidente con l'origine del sistema di riferimento cartesiano; su questa sfera ho poi disegnato alcuni meridiani e paralleli calcolati nel seguente modo:
Ho estruso degli elementi a sezione rettangolari lungo queste linee coordnate:
Fabiana Riparbelli
Lun, 12/12/2011 - 19:36
Collegamento permanente
piccoli progressi
Allora, ho trovato questo comando che penso potrà esserci molto utile. Si chiama "Proietta", funziona così: disegno una superficie nello spazio e disegno un curva sul piano orizzontale in corrizpondenza di questa superfcie; questo comando proietta un qualsiasi tipo di curva su una superficie qualsiasi adattando la curva alla forma di quest'ultima. Facendo un esempio pratico, ho disegnato una spirale e sopra di essa una sfera, poi ho chiesto a Rhino di proiettare la spirale sulla sfera e questo è il risultato:
Dove si vede in rosso la spirale piana, in nero la proiezione sulla sfera, ed in giallo le linee di costruzione della sfera. Per verificare che queste linee venissero lette correttamente ho importat il file in autocad ed ho ripetuto il processo di estrusione, fino ad arrivare ad un modello tridimensionale che ho potuto renderizzare in 3Dstudio:
Fabiana Riparbelli
Sab, 17/12/2011 - 21:49
Collegamento permanente
Passaggio successivo
Ho modellato una superficie seguendo un percorso che era meglio orientato. In particolare questa prova vuole essere da una parte una sintesi, o meglio, una via d'utilizzo delle nozioni fin qui apprese a livello di modellazione di software; dall'altra una prima interazione con il programma di calcolo meccanico. C'è quindi un obiettivo aggiunto, che ha comportato diversi problemi.
Il primo passo è stata la creazione della superficie in Rhino. Questa è stata generata e modellata a partire da un rattangolo di dimensioni 25x15 m immaginato orientato secondo gli assi x ed y, per poi essere suddivisa in mesh triangolari facilmente leggibili da SAP. Successivamente ho disegnato sulla proiezione a terra un graticcio 1x1 e l'ho poi proiettato (tramite il comando "proietta") sulla superficie:
Nella figura si vedono le linee in rosso che sono le linee proiettate sulla superficie, e quelle in viola che appartengono al piano xy e definiscono la figura di partenza.
Come prima cosa ho provato ad importare la superficie in SAP per verficare che venisse letta correttamente:
Come si vede nella figura sottostante, selezionando tutte le linee sembra non ci siano imprecisioni:
Questo passaggio, grazie ad una verisone più aggiornata di SAP, non ha creato problemi. Il passaggio ostico è stata l'importazione del solo graticcio.
Salvando il file dxf da Rhino, Sap non leggeva nessuna linea. Facendo diversi tentativi di capirne il motivo ho notato che le linee proiettate, ovvero quelle che formavano il graticcio, venivano lette male sia in Rino che in Autocad, per cui risultava impossibile anche eseguire lo sweep. Lavorando su Autocad ho capito che Sap legge solo le polilinee3D, mentre la modellazione fatta fino ad ora si basava su spline e polilinee2D. Sono sicura che esiste un modo per convertire un elemento nell'altro, ma è più difficile da trovare di quanto credessi; quello che ho fatto è stato ricalcare in Autocad il graticcio con le polilinee3D, per poi importarlo in SAP ed avre la possibilità di esegurne uno sweep:
Come si può vedere a questo punto l'importazione non da problemi, almeno apparentemente.
Fabiana Riparbelli
Dom, 18/12/2011 - 14:56
Collegamento permanente
Render
Ho provato a renderizzare il graticcio, allego le immagini:
Fabiana Riparbelli
Dom, 08/01/2012 - 12:27
Collegamento permanente
Come importare un graticcio in SAP
Ho risolto molti problemi, sebbene ancora non tutti, riguardo l'importazione in SAP. Il metodo che avevo usato risultava lungo (poichè dovevo ricalcare il graticcio in autocad) e poco utile, poichè non venivano riconosciuti i nodi all'intersezione delle curve.
Per migliorare questi aspetti sono partita da Rhino.
Il graticcio che ho disegnato tramite il comando "Proietta" non riconosceva i nodi poichè si tratta di polilinee continue:
Ho provato ad aggiungere i punti, con il comando "Punto" di Rhino nelle intersezioni, ma SAP non è in grado di leggerli. Per cui ho pensato che l'unico modo per far riconoscere i nodi a SAP sarebbe stato quello di spezzare le curve nei punti di intersezone. Il metodo più veloce che ho trovato è il seguente: Seleziono tutte le curve e uso il comando "Intersezione":
Questo comando genera solo punti laddove riconosce delle intersezoni, nel caso non le riconosca è possibile aggiungerli manualmente. Poi ho usato il comando "Suddividi", dicendo che tutte le curve erano gli oggetti che volevo suddividere, mentre i punti erano gli oggetti di taglio:
In questo modo Sap è in grado di riconoscere con precisione tutti i nodi. Infine il passo fondamentale è stato quello di NON usare un file dxf, ma di salvare il disegno in formato IGES (.igs) che, a quanto pare, è di più facile lettura. A questo punto il passaggio tra Rhino e SAP è immediato:
Ho selezionato il file IGES da importare, in questo caso SAP non ti chiede quale layer vuoi utilizzare, ma importa tutti i layer del disegno, per cui è bene pulire il file direttamete da Rhino:
Ci sono però ancora dei problemi. SAP crea dei punti di discontinuità:
Ci sono dei comandi di Rhino che mi possono aiutare a semplificare le curve, lavorando sulle tolleranze si dovrebbe riuscire a ridurre il numero di linee ed a far leggere il file senza più errori.
Fabiana Riparbelli
Dom, 08/01/2012 - 13:01
Collegamento permanente
Come non detto, questi problemi sono risolti...
Era un problema di facile soluzione. Quando si importa il file in SAP bisogna stare attenti alle unità di misura:
Lo stesso File non presenta più problemi se importato con le unità di misura giuste. Inoltre ho provato a ridurre il numero di Frames, prima da SAP utilizzando "Merge Joints": la tolleranza più alta che non distorce la geometria è di 0,001 e non ha effetto sul numero di Frames (3942). Così ho lavorato su Rhino con il comando "Semplifica Curve" che ha ridotto il numero a 3173. Ripetendo più volte il comando si arriva ad una approssimazione massima di 3168 Frames.
Per verificare l'attendibilità del metodo ho ripetuto tutti i passaggi per un secondo graticcio la cui tessitura è inclinata a 45°: Da Rhino ho utilizzato, in ordine, i comandi : INTERSEZIONE; SUDDIVIDI; SEMPLIFICA (Due volte) SALVA IGES.
Poi in SAP ho cambiato l'unità di misura del disegno in KN, m, C, ed ho importato il File senza nessun problema.
Fabiana Riparbelli
Mer, 11/01/2012 - 19:21
Collegamento permanente
curve geodetiche
Ho provato a realizzare un modello utilizzando le curve geodetiche. Ho lavorato solo su Rhino e 3Dstudio; come prima cosa ho generato e modellto la superficie tramite i comandi di "Loft" e "Punti di Controllo"
Ho poi diviso le curve generatrici in 40 pezzi (misuravano cirvca 40 metri) ed ho unito i punti tramite il comando "CurvaGeodetica", sia passando per la curva centrale (Rosso) sia andando direttamente da parte a parte (Verde):
Ho deciso di provare a renderizzae un modello estrudendo le geodetiche in Rosso ed aggiungendo due curve intermedie lungo il lato lungo (in blu).
Sono linee tracciate in modo pressochè casuale, nel senso che immagno si possano disegnare queste curve con un criterio che tenga in considerazione le conseguenze meccaniche che vi sarebbero nel caso in cui una curva geodetica rappresentasse una trave, o un elemento struttrale. Di fatto questo passaggio logico mi sfugge, come mi sfugge, non avendo ancora approfondito l'argomento, il significato reale di queste curve; ad ogni modo forse questo esercizio, agli occhi dei più esperti, può aiutare a capire se si tratta di un approfondimento sarebbe o meno necessario fare.
Fabiana Riparbelli
Sab, 14/01/2012 - 20:47
Collegamento permanente
Prova di Calcolo
Fabiana Riparbelli
Dom, 22/01/2012 - 19:03
Collegamento permanente
Altre Analisi
Ho eseguito l'analisi, come precedentemente descritta, sulla stessa superficie, prima considerando un secondo graticcio, e poi considerando la superficie stessa una soletta in c.a.
SECONDO GRATICCIO:
Riporto la configurazione iniziale:
ed i grafici delle sollecitazioni di Momento:
Taglio:
e Normale:
Ed infine la deformata:
SOLETTA in C.A.
L'importazione della superficie come shell (tramite salvataggio in file dwx) non ha riportato problemi:
Ho vincolato l'intero perimetro e cominciato l'analsi.
Ho riportato tutti i valori massimi dei risultati che mi sono comparsi, senza capirne però la vera natura. In attesa di studiare più approfonditamente il concetto di shel e di membrana, allego i grafici dei suddetti risultati:
CONCRETE DESIGN_Nmax:
SHELL STRESSES_Smax:
SHELL STRESSES_SmaxV:
RESULTANT FORCES_Fmax:
RESULTANT FORCES_Mmax:
RESULTANT FORCES_Vmax:
Fabiana Riparbelli
Mer, 01/02/2012 - 01:15
Collegamento permanente
Le linee di curvatura!
Ho provato a studiare una superficie di cui conoscevo l'equazione per cercare di disegnarvi sopra le linee di curvatura ed utilizzarle poi per il calcolo strutturale. La superficie in questione è un paraboloide ellittico della forma z = x^2 + y^2, ho svolto tutti i calcoli del caso a mano e li ho rassunti in questa pagina:
A questo punto sono passata a Rhino. Per disegnare il paraboloide ho utilizzato il comando "Paraboloide".
Il caso preso in considerazione è quello di un paraboloide generato dalla rotazione di una parabola z = x^2 intorno all'asse delle z, per cui ho individuato il vertice (0,0) ed il fuoco (0,1), ed immesso i dati.
Sono poi passata allo script. Le famiglie di curve individuate sono le proiezioni delle linee di curvatura sul piano xy, per cui ho riportato le equazioni nello script prima delle circonferenze:
E poi delle rette:
Ottenedno il seguente risultato:
A questo punto ho utlizzato il comando "Proietta" per ottenere la proiezione di cueste curve sulla superficie:
Disegnandovi, appunto, le linee di curvatura. Ho fatto poi un'ulteriore considerazione:
per prima cosa tengo a precisare che sono assolutamente certa di questo risultato poichè l'ho confrontato anche con gli esercizi svolti del testo "Problemi di geometria differenziale";
Detto ciò, essendoci spesso interrogate sulla natura dell' "analisi zebra" di rhino, ho svolto l'analisi su questa superficie. Una volta svolta ci viene data la possibilità di scegliere se visualizzare le linee zebra verticalmente o orizzontalmente, in direzioni, quindi, tra loro perpendicolari. Questo ha fatto sorgere il dubbio che le linee zebra altro non fossero che la rappresentazione grafica delle due famiglie di linee di curvatura. Ma svolta l'analisi del caso, mentre la rappresentazione della famiglia di linee verticali sembrava potesse confermare questa teoria:
Quella nella direzione orizzontale ha cancellato ogni dubbio:
Quindi le linee zebra NON sono le linee di curvatura, il che spiegherebbe anche l'assenza di un apposito comando di Rhino che fosse in grado di disegnarle, come accade infatti con le curve geodetiche.
Come ultima cosa, prima di passare all'analisi strutturale, ho provato ad utilizzare il linguaggio dello script per generare una superficie apparentemente più complessa sulla quale vorrei svolgere i medesimi calcoli: z = sinx siny:
Ed ha funzionato!
Fabiana Riparbelli
Sab, 11/02/2012 - 12:44
Collegamento permanente
Prove in SAP
Ho eseguito il calcolo in SAP del paraboloide ellittico. Ho provato anche a fare l'analisi considerandolo una shell, ma non potendone capire i risultati credo sia più importante adesso cercare di vedere quali passaggio ho fatto per calcolare il graticcio e vedere se il procedimento è corretto o se non considero alcuni elementi
Ho eliminato le aste del verice perchè so che il sistema funziona ugualemente, e mi semravano troppo ravvicinate; tuttavia non credo sia una scelta dovuta.
L'impostazione dell'analisi è la seguente:
VINCOLI a terra: CERNIERE
NODI: INCASTRI (non ho assegnato nulla in particolare ai nodi perchè SAP dovrebbe riconoscerli come incastri di default)
CARICHI: 5kN distribuito + peso proprio della struttura
MATERIALE: ACCIAIO con sezioni Rettangolari 10x15cm di spessore 6,5 mm
A questo punto avvio l'analisi. I risultati che cerco, in questo caso, sono i valori massimi della normale (Axial Force):
Del taglio (shear 2-2):
e del Momento (moment 3-3):
Inoltre posso guardare la deformata per verificare che sia consona alla distribuzione dei carichi:
Fatto questo non so cos'altro cercare.
Fabiana Riparbelli
Sab, 11/02/2012 - 13:16
Collegamento permanente
Prove in SAP 2
Ho eseguito lo stesso calcolo su una semisfera.
Ho assegnato stessi carichi, stesso materiale e stessa sezione. Gli elementi strutturali corrispondono a meridiani e paralleli, quindi alle linee coordinate; inoltre ogni direzione è una direzione principale, quindi si può dire che corrispondano anche alle linee di curvatura; nel caso dei meridiani, inoltre, essi rappresentano le curve geodetiche che uniscono i punti appartenenti alla circonferenza di base con il vertice. I risultati sono i seguenti:
Sforzo Normale:
Taglio:
Momento:
E la deformata:
Fabiana Riparbelli
Sab, 11/02/2012 - 14:27
Collegamento permanente
Prove in SAP 3
Ho rifatto il calcolo dei graticci (post #22 e #23). Avevo incastrato la struttura ed avevo assegnato una sezione troppo grande per un reticolo così fitto. I termini per l'analisi, in entrambi i casi, sono i seguenti:
VINCOLI: CERNIERE
MATERIALE: ACCIAIO con sezione rettangolare 20x10 cm di spessore 4 mm
CARICHI: 5kN distribuito + peso proprio
NODI: INCASTRI (assegnati in automatico da SAP)
Ho quindi analizzato i due casi.
1) GRATICCIO (1x1 m), con inclinazione delle aste a 90°.
Momento:
Taglio:
Normale:
Deformata:
2) GRATICCIO (1x1 m), con inclinazione delle aste a 45°.
Momento:
Taglio: (qui il grafico mi sembra strano)
Normale:
Deformata:
Fabiana Riparbelli
Sab, 11/02/2012 - 18:32
Collegamento permanente
Mathematica
Oggi ho installato la versione 8.0 di Mathematica ed ho cominciato a vedere come funziona perchè sulle forme parametriche è possibile calcolare le equazioni delle due famiglie di linee di curvatura, ma fare questo calcolo a mano è possibile solo su superfici descritte da un'equazione molto semplice, e comunque, arrivati ad un certo punto del calcolo, le cose si complicano inevitabilmente.
Stavo cercando di trovare le linee di curvatura della superficie z = Sin(x)Sin(y) che ho sviluppato con lo script e pubblicato nel post #24; in Mathematica viene rappresentata così:
Svolgendo i calcoli si arriva ad avere un'eqazione di questa forma:
Da qui in poi gestire il calcolo a meno diventa davvero complicato. Bisogna svolgere un sistema per trovare i rispettivi valori di A e B, ma la semplificazione migliore, ad ora, è la seguente:
Che va sostituto all'equazione in B. Al di là di questo esempio credo comunque sia utile imparare ad utilizzare il programma, per non essere bloccata dal calcolo nel caso si scegliesse di studiare una forma parametrica.
Fabiana Riparbelli
Mar, 13/03/2012 - 18:26
Collegamento permanente
Ho fatto questo ragionamento...
Mi piacerebbe portare due metaprogetti, una geometria gestibile a livello parametrico ed una geometria libera. Credo sia il modo migliore di rappresentare questa ricerca, per diversi motivi: il primo è che i due approcci, visti insieme, mettono in evidenza uno i limiti dell'altro e risultano meglio comprensibili; il secondo è che tutto il lavoro fatto rende possibile la gestione dell'uno e dell'altro tipo di forma, e limitarsi ad approfondirne una sola mi sembra non del tutto esaustivo. A questo proposito ho sviluppato due ipotesi sulle queli si potrebbe lavorare:
FORMA PARAMETRICA. Generta tramite il seguente script:
Ovvero:
Che risulta fin troppo semplice forse, ma la modifica dell'altezza tramite lo script è più difficoltosa di quanto mi aspettassi. Non so se dettato dalla stanchezza, ma io c'ho trovato un certo fascino, quindi ho ipotizzato una tessitura:
Vista in tre dimensioni:
Non sono andata oltre su questo esempio perchè ho diverse riserve riguardo la geometria.
FORMA LIBERA. Generata a partire da quattro curve (in rosso nella figura) mediante il comando Loft, e riferendomi ad una base composta di due circonferenze (in nero) di 80 e 40 metri di diametro:
Nel processo di modellazione tramite punti di controllo ho anche deciso di inserire delle bucature (cerchi in blu nella figura), ed ho ottenuto il seguente risultato:
In questo caso sono andata avanti perchè, sinceramente, questa forma mi piace. Ho provato quindi ad esportala in SAP2000; la prima divisione in mesh è stata effettuata con una densità pari ad 1.0:
Ma era impossibile lavrarci in SAP, evidentemente pesa troppo ed il programma gira lentissimo. Allora ho creato una seconda mesh con densità 0.7, sulla quale è stato possibile lavorare:
Prima di passare a SAP ho tentato di generare una tessitura. Dapprima ho utilizzato un sistema di riferimento polare (con origine coincidente con il centro della circonferenza più piccola) ed ho generato una grid shell di linee coordinate:
Esteticamente questa grid-shell non ha grande valore ed andrebbe disegnata con più accuratezza, ma ho comunque provato a fare un'analisi per rendermi conto di quanto la geometria fosse getibile.
Come ultima cosa, prima di passare al SAP, ho provato a generare una grid-shell composta di curve geodetiche e, con mia grande sorpresa, il comando su questa superficie non funziona. Mi spiego meglio: seguendo lo stesso procedimento di sempre ho suddiviso i limiti interni ed esterni della superficie in 60 parti ed ho poi provato a generare le geodetiche da punto a punto, ma il risultato è stato il seguente:
Probabilmente è una geometria troppo complessa anche per Rhino. Questo è un aspetto che vorrei capire meglio, appena possibile cercherò di analizzarlo.
Fabiana Riparbelli
Mar, 13/03/2012 - 19:32
Collegamento permanente
Seguito del post precedente
Vediamo le analisi strutturali in SAP, premetto che ad entrambi ho assegnato un carico distribuito pari a 4 kN e non ho considerato il contributo del peso proprio.
GRID-SHELL. Il File viene letto senza errori:
Il materiale è acciaio, sezione scatolare di altezza 15 cm, larghezza 10 cm e spessore 6,5 mm. Riporto solo il grafico della sollecitazione normale poichè sia la deformazione sia i valori di taglio e momento sono trascurabili. Riguardo lo sforzo assiale, invece, il valore massimo è di 1475 kN (il cerchio più grande), ma i punti di "picco" sono locali e si potrebbe intervenire sulla geometria per correggerli:
SHELL. Ho importato la shell e verificato che venissero letti tutti gli elementi:
A questo punto ho asegnato il materiale ed il carico. Stavolta ho studiato prima di fare l'analisi per capire bene quali parametri andare a toccare: ho scelto come carico Area Loads e poi Uniform (Shell) che viene applicato alla superficie mediana della shell (che coincide con la superficie importata); sono poi andata a definire la sezione del'area tramite questa finestra:
Ho importato il file come "Shell", per cui in Type potevo scegliere solo tra le opzoni Thin e Thick, ho scelto Thin nonostante la tipologia Thick sia più accurata. La scelta del tipo Thin, però, è consgliabile quando si analizzano mesh distorte o quando si è certi che la deformazione a taglio sia trascurabile, ed essendo la deformazione a taglio importante solo quando lo spessore dell'area è più di 1/5 o 1/10 della luce, ho reputato Thin la scelta migliore. Ho impostato lo spessore (thickness) di 20 cm; questo valore, se ho capito bene, verrà utilizzato per caclolare la rigidezza della membrana (membrane) e la rigidezza torsionale (Bending), ed è uso comune stabilire lo spessore della membrana ed utilizzare quello stesso valore nella voce Bending. A questo punto ho avviato l'analisi, vediamo la deformata:
In cui si può notare che una parte della geometria si deforma troppo rispetto al resto.
Sempre se ho capito bene, il risultato che devo andare a guardare è Fmax, che fa parte delle Resultant Forces, anche dette Shear Element Internal Forces, da cui deduco che Fmax sia il valore massimo dello sforzo di membrana, di cui vengono rappresentati i valori medi mediante lo spettro di colori generato da SAP:
Non so bene quali siano i limiti entro i qual è ragionevole pensare ad un dimensionamento, ma i valori per ora mi sembrano essere molto elevati.
Per concludere, ho provato a renderizzare questa geometria per verificarne l'effetto visivo:
Fabiana Riparbelli
Sab, 24/03/2012 - 17:12
Collegamento permanente
Modifiche forma libera
Nel Post #29 avevo individuato almeno tre punti della forma libera in cui le sollecitazioni avevano valori estremamente più alti della media. Ho quindi provato a correggere quei punti variandone la geometria. Ho fatto diversi tentativi e li ho analizzati su SAP come shell, ottenendo i seguenti risultati:
La modifica numero 3 ha dei valori degli sforzi gestibili, di seguito riporto i grafici relativi ad Fmax:
Ed Smax:
Da queste immagini si capisce che i valori di massimo e di minimo sono locali (potrebbero essere considerati puntali), mentre mediamente gli sforzi sono molto più bassi.
Ho preso per buona questa gemetria ed ho ipotizzato una GRID-Shell che vi si adattasse:
Le curve in bianco sono 80, ed hanno origine nel centro della circonferenza piccola (tramite la quale ho costruito la geometria). Le curve in blu, invece, sono curve geodetiche. Sempre nel post #29 avevo evidenziato un problema di Rhino, ovvero che non riusciva a disegnare le curve geodetiche su questa forma: questo è vero in senso trasversale, mentre longitudinalmente le curve vengono disegnate senza problemi. Per costruire questa GRID-Shell, quindi, ho suddiviso in 10 parti alcune delle curve in bianco (che sono a tutti gli effetti linee coordinate), e le ho collegate tramite il comando "CurvaGeodetica". A questo punto ho condotto l'analisi in SAP: ho utilizzato scatolari in acciaio, variandone la sezione:
Ho scelto poi di utilizzare una sezione 20x40. Come si può vedere con una sezione più grande (25x50) i valori delle sollecitazioni si abbassavano ulteriormente, tuttavia la differenza con le sollecitazioni della prova precedente mi è sembrata troppo piccola in relazione all'aumento del materiale, ed ho quindi preferito considerare migliore la sezione 20x40. Riporto i grafci dello Sforzo Assiale:
Del Taglio:
E del Momento:
Anche in questo caso i valori medi delle sollecitazioni sono molto più bassi di quelli massimi o minimi. Si può quindi procedere individuando i punti critici e correggendone la geometria. Nel frattempo ho fatto una prova di render anche per la GRID-Shell:
DanieleNardone
Mar, 27/03/2012 - 10:10
Collegamento permanente
ottimo lavoro!
Ciao Fabiana,
è un po' che non commento il tuo blog, il tuo lavoro va avanti è vedo che hai raggiunto buoni risultati, sei partita con un concetto molto più astratto del mio, e sei arrivata un po' al mio punto di partenza... mi sembra bello vedere quanto lavoro può essere fatto prima di pansare ad una forma anche se astratta.. ti faccio i miei complimenti.. soprattutto per averlo descritto step by step.
la forma in se comincia ad essere molto interessante a mio avviso... se fosse tutta una superficie unica e liscia trattata come un fazzolettone sarebbe veramente interessante.. ma questo è un mio giudizio personale... esoprattutto porta non poche complicazioni strutturali... per quanto riguarda invece le correzioni geometriche per ottenere sforzi sufficientemente accettabili nel mio blog c'è molto materiale. io mi sono scontrato con delle trazioni tremende e la geometria della mia forma ha dovuto compensare queste grandissime trazioni. se hai domande a riguardo sono tutto orecchie.
continuo a seguire con molto interesse il tuo blog.. buon lavoro.
Fabiana Riparbelli
Gio, 29/03/2012 - 11:24
Collegamento permanente
Ciao Daniele!
DanieleNardone
Gio, 12/04/2012 - 08:28
Collegamento permanente
buon lavoro..
mi raccomando non dimenticare di scrivere quando hai intenzione di discutere la tesi che non voglio perdermela.
A presto
Daniele
Fabiana Riparbelli
Gio, 12/04/2012 - 09:11
Collegamento permanente
Forma parametrica
(Per Daniele: appena avrò conferma ti scriverò la data!)
Intanto ho modificato lo script della forma parametrica che avevamo scelto per adattarla ad una stanza rettangolare, immaginandola quindi come un oggetto ornamentale. Non ho esguito alcun calcolo perchè volevo essere prima certa dell'effetto, questo è il render:
(Ho fatto molte prove con diversi tipi di luci)
Adesso vorrei riuscire ad utilizzare questa forma, con le dovute modifiche, ad una scala un pò più grande, o comunque in condizioni in cui risulti portante. Per quanto riguarda la forma libera invece ho risolto il problema della fessurazione per i carichi verticali, ma ho dei dubbi circa il sisma di cui parleremo meglio domani.
GinevraSalerno
Ven, 13/04/2012 - 10:53
Collegamento permanente
la bellezza delle forma parametrica
cara Fabiana
la forma parametrica è bellissima. Prendi in considerazione che a dimensioni più grandi piena non resiste e sarebbe MERAVIGLIOSO se fosse nervata con le nervature dirette lungo le linee di curvatura.
Ginevra Salerno
Fabiana Riparbelli
Gio, 19/04/2012 - 15:28
Collegamento permanente
Perpendicolarità Direzioni Principali
Allora, cito testualmente quanto riportato dal testo Schaum a pagina 185:
Fabiana Riparbelli
Gio, 19/04/2012 - 15:32
Collegamento permanente
Forma Libera
Allego anche un'immagine che ho sempre dimenticato di postare di com'è diventata la forma libera a seguito di tutte le modifiche dovute al calcolo, ora dovrebbe funzionare:
Fabiana Riparbelli
Gio, 19/04/2012 - 21:06
Collegamento permanente
Passi avanti
Ho provato a calcolare le linee di curvatura del paraboloide ellittico. Ho rifatto i calcoli in Maple trovando i coeficienti fondamentali:
Poi sono passata a RhinoScript ed ho provato a disegnare una sola linea di curvatura come una successione di punti, il risultato è il seguente:
I punti seguono effettivamente la linea di curvatura. Quindi ho ripreso in mano il file Maple del "fungo" ed ho ricontrollato ogni passaggio utilizzato per calcolare i coefficienti fondamentali, che risultano:
Quindi sono tornata sullo script ed ho provato a disegnare le linee di curvatura, prima in una direzione e poi nell'altra:
Quelle che vengono fuori sono le linee coordinate, ma se questo procedimento è corretto non caisco perchè i coefficienti fondamentali F ed M non sono uguali a zero. Ho comunque costruito la grid-shell:
L'unica spiegazione possibile è che nel generare la successione di punti nello script abbia reso un parametro costante. Se così fosse queste sarebbero le linee coordinate, non per forza linee di curvatura.
Fabiana Riparbelli
Gio, 19/04/2012 - 21:33
Collegamento permanente
Passo indietro
Quelle erano linee coordinate. Questa dovrebbe essere la nuvola di punti che identifica le linee di curvatura, sto cercando di capire come isolare una sola direzione perchè in questo modo non riesco a ricostruirle con precisione: