SESTA ESERCITAZIONE: Esercitazione sulle travi Virendeel

ESERCIZIO 1: TRAVE VIRENDEEL A SBALZO

SCHEMA INIZIALE:

Per risolvere la trave Virendeel, essa può essere trattata come un telaio Shear-Type sdraiato orizzontalmente;

quindi supponiamo che:

- i pilastri siano infinitamente rigidi,

- i ritti siano deformabili

- per effetto delle forze esterne i pilastri traslano, senza deformarsi, di una quantità δ

DEFORMATA:

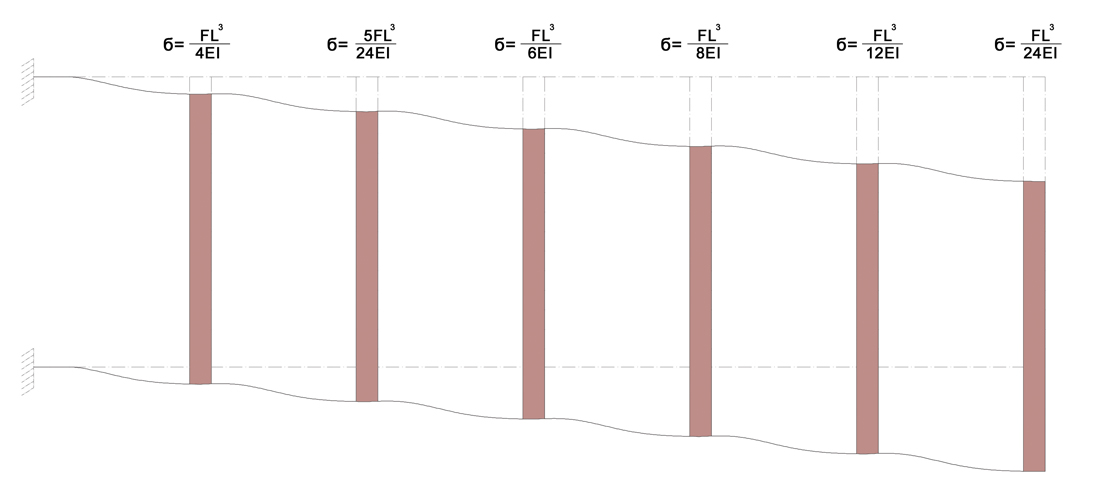
OSSERVAZIONI:

Conoscendo il valore dello spostamento trasversale  δ è possibile determinare il valore delle caratteristiche di sollecitazione e delle rigidezze dei traversi.

FONDAMENTALE:

Avvalendoci dello schema noto riguardante la trave doppiamente incastrata, risolto in classe con le equazioni della linea elastica, possiamo risolvere la trave Virendeel.

                                                                                                    SCHEMA NOTO

                                                                               

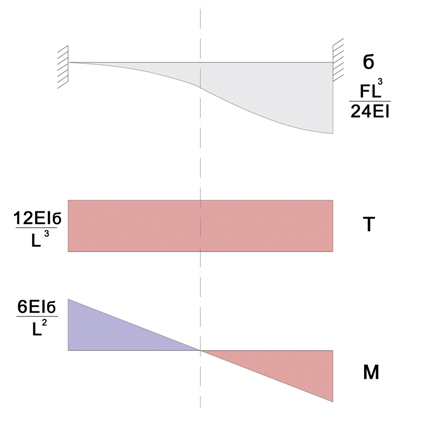
RISOLUZIONE:

1-TAGLIO NELLE TRAVI

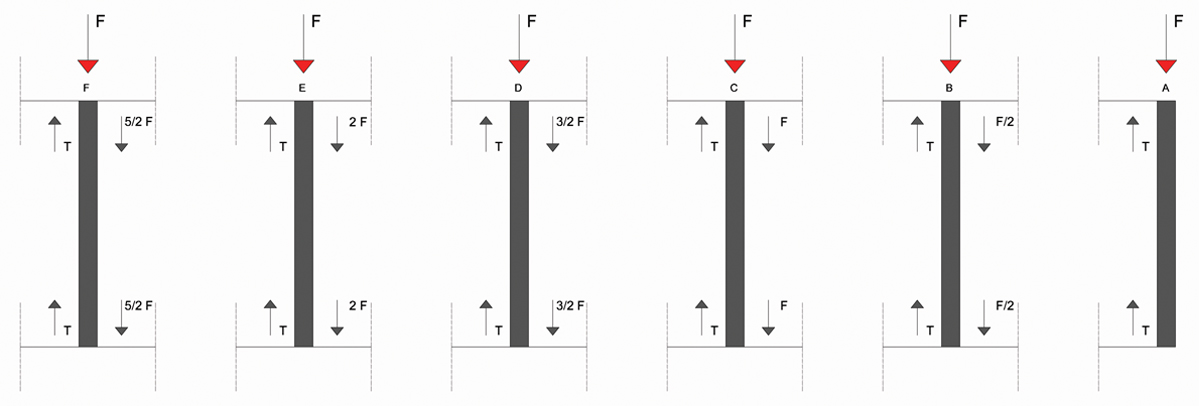
N.B: per ogni incognita spostamento avremo un’equazione alla traslazione verticale.

A.      F= 2T

T= 12EIδ/L³

F= (24EI/L³)×δ

δ= FL³/24EI

T= (12EI/L³)×(FL³/24EI)= F/2

B.      F + F/2 + F/2= 2T

F + F/2 + F/2= (24EI/L³)×δ

2F= (24EI/L³)×δ

F= (12EI/L³)×δ

δ= FL³/12EI

T= (12EI/L³)×(FL³/12EI)= F

C.     F + F + F= 2T

F + F + F= (24EI/L³)×δ

3F= (24EI/L³)×δ

F= (8EI/L³)×δ

δ= FL³/8EI

T= (12EI/L³)×(FL³/8EI)= 3/2F

D.     F + 3/2F + 3/2F= 2T

F + 3/2F + 3/2F= (24EI/L³)×δ

4F= (24EI/L³)×δ

F= (6EI/L³)×δ

δ= FL³/6EI

T= (12EI/L³)×(FL³/6EI)= 2F

E.     F + 2F + 2F= 2T

F + 2F + 2F= (24EI/L³)×δ

5F= (24EI/L³)×δ

F= 24EI/5L³)×δ

δ= 5FL³/24EI

T= (12EI/L³)×(5FL³/24EI)= 5/2F

F.     F + 5/2F + 5/2F= 2T

F + 5/2F + 5/2F= (24EI/L³)×δ

6F= (24EI/L³)×δ

F= 4EI/L³)×δ

δ= FL³/4EI

T= (12EI/L³)×(FL³/4EI)= 3F

2-MOMENTO NELLE TRAVI

N.B: per calcolare il momento basta moltiplicare la forza di taglio complessiva agente su quella parte di trave per il suo braccio L/2.

A.      (F/2)×(L/2)= FL/4

B.      F × L/2= FL/2

C.      3/2F × L/2= 3/4 FL

D.      2F × L/2= FL

E.      5/2F × L/2= 5/4 FL

F.      3F × L/2= 3/2 FL

3-MOMENTO NEI RITTI

N.B: Nella trave Virendeel vale  ancora M=EIχ , ma χ=0 e EI=∞, ma M è ancora un numero Reale.

Facendo l'equilibrio ai nodi ci accorgiamo che, questi, non sono in equilibrio; perciò, per garantire l'equilibrio complessivo della struttura, anche sui ritti insisterà un momento che sarà semplicemente calcolato effettuando, appunto, l'equilibrio al nodo.

A.      ribaltando il momento per continuità= FL/4

B.      (FL/4) + (FL/2)= 3/4 FL

C.      (FL/2) + (3/4FL)= 5/4 FL

D.      (3/4FL) + (FL)= 7/4 FL

E.      (FL) + (5/4FL)= 9/4 FL

F.      (5/4FL) + (3/2FL)= 11/4 FL

4-TAGLIO NEI RITTI

N.B: per determinare il valore del Taglio, prodotto dalla presenza del momento derivante dall'equilibrio al nodo, sommerò i valori dei momenti all'estremità e li dividerò per il braccio; (m1+m2)/L.

A.      [(FL/4)+(FL/4)]/2L= F/4

B.      [(3/4FL)+(3/4FL)]/2L= 3/4F

C.      [(5/4FL)+(5/4FL)]/2L= 5/4F

D.      [(7/4FL)+(7/4FL)]/2L= 7/4F

E.      [(9/4FL)+(9/4FL)]/2L= 9/4F

F.      [(11/4FL)+(11/4FL)]/2L= 11/4F

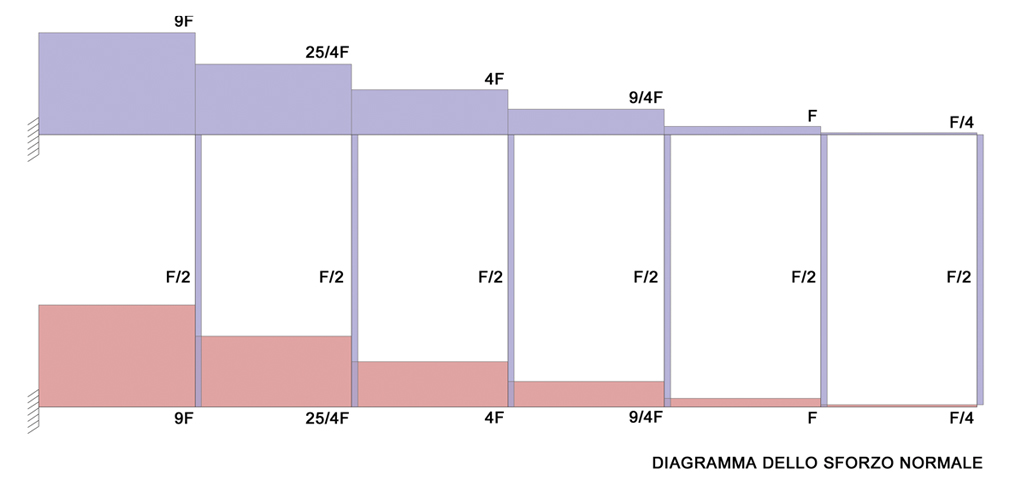
5-SFORZO NORMALE 

N.B: per determinare il valore dello Sforzo Normale, basta ribaltare il valore del taglio presente nei ritti sulle travi e il valore del taglio presente nelle travi sui ritti tenendo conto delle forze esterne "F" applicate sui nodi.

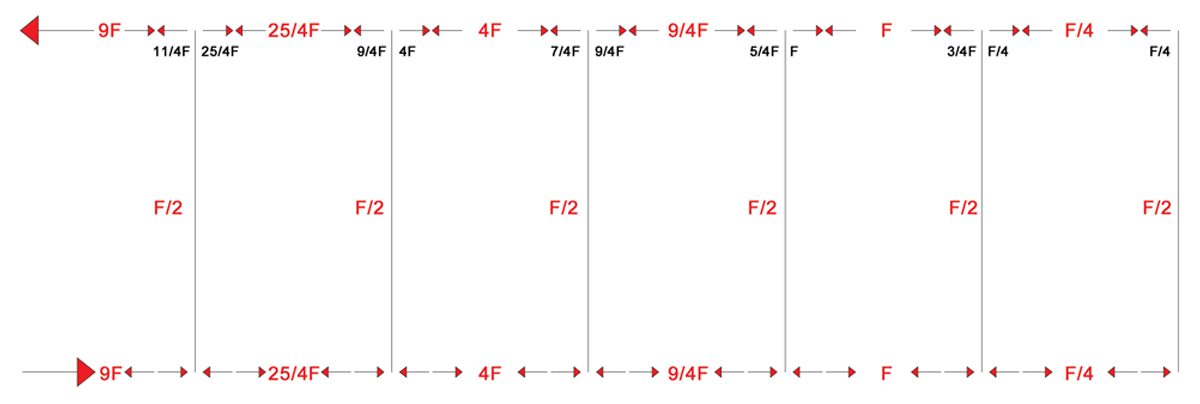
6-DIAGRAMMI

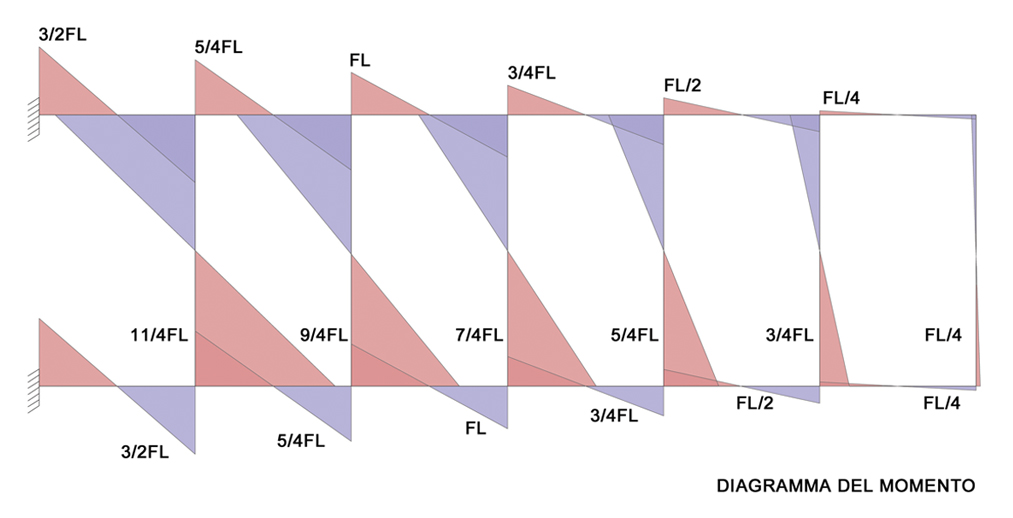
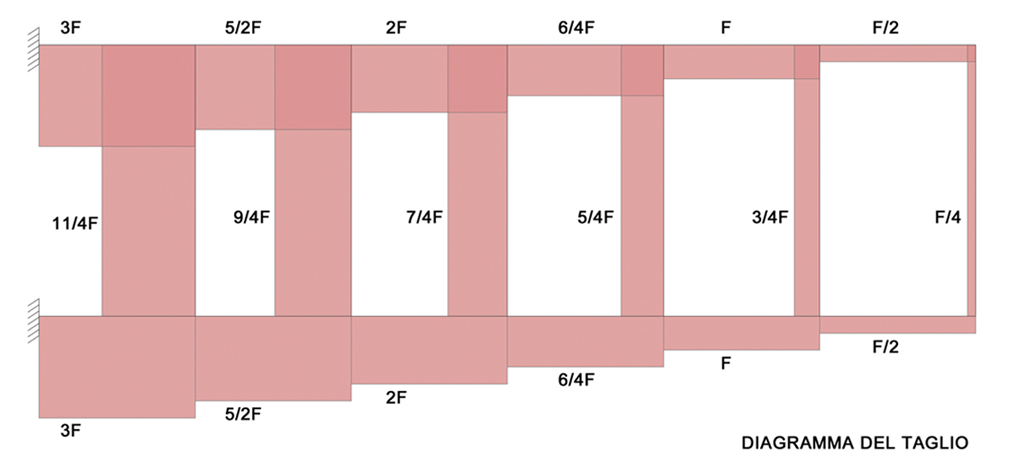
ESERCIZIO 2: TRAVE VIRENDEEL DOPPIAMENTE INCASTRATA

OSSERVAZIONI:

Questo secondo esercizio risulta essere molto simile a quello svolto precedentemente; in questo caso però abbiamo una trave Virendeel doppiamente incastrata su entrambe la estremità. Un dato molto importante, che facilita il procedimento risolutivo dell'esercizio, è la simmetria della struttura e dei carichi esterni. Possiamo quindi analizzare solamente la metà di sinistra.

Ovviamente fanno fede tutte le considerazioni fatte nell'esercizio n.1 perciò lo svolgimento di questo sarà molto più immediato

SCHEMA INIZIALE:

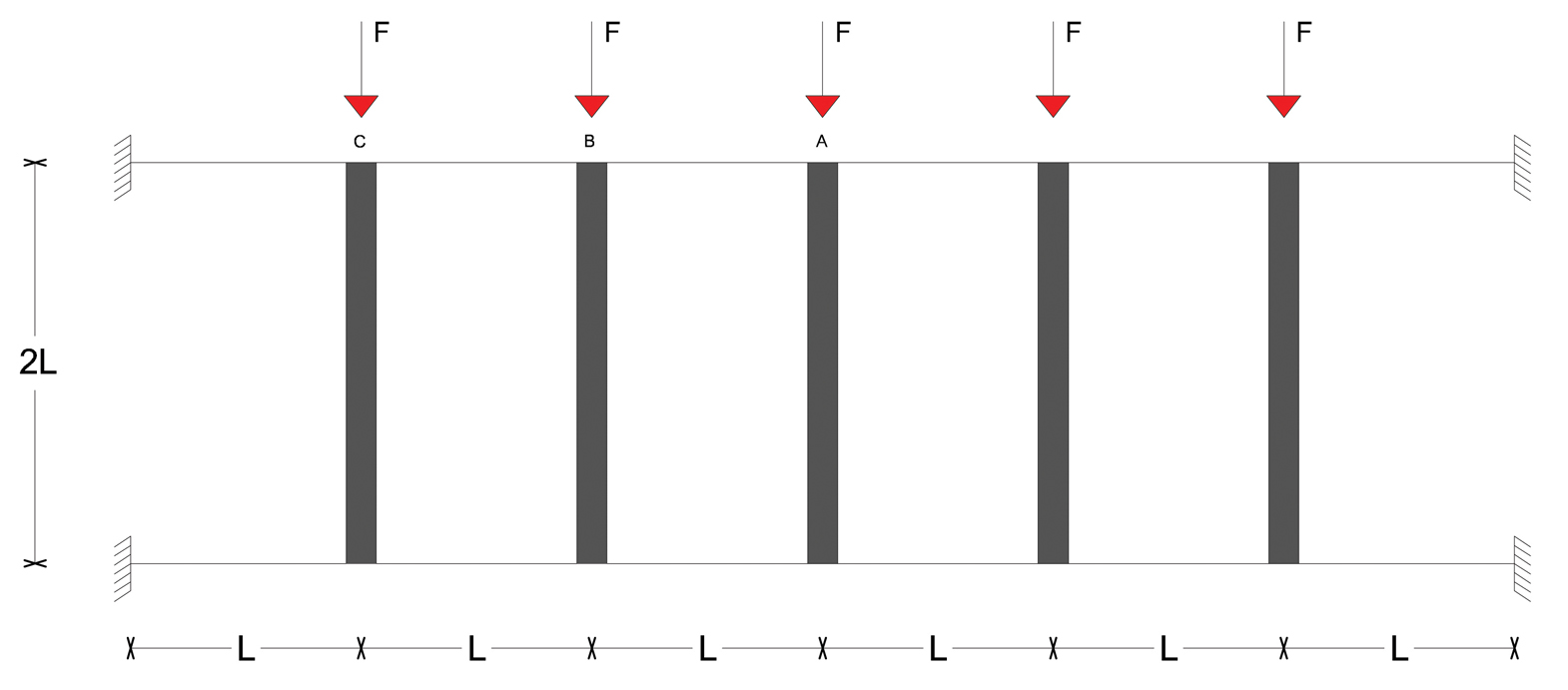
DEFORMATA:

RISOLUZIONE:

1-TAGLIO NELLE TRAVI

A.      F= 4T

T= 12EIδ/L³

F= (48EI/L³)×δ

δ= FL³/48EI

T= (12EI/L³)×(FL³/48EI)= F/4

B.      F + F/4 + F/4= 2T

F + F/4 + F/4= (24EI/L³)×δ

3/2F= (24EI/L³)×δ

F= (16EI/L³)×δ

δ= FL³/16EI

T= (12EI/L³)×(FL³/16EI)= 3/4 F

C.     F + 3/4 F + 3/4 F= 2T

 F + 3/4 F + 3/4 F= (24EI/L³)×δ

5/2F= (24EI/L³)×δ

F= (48EI/5L³)×δ

δ= 5FL³/48EI

T= (12EI/L³)×(5FL³/48EI)= 5/4 F

2-MOMENTO NELLE TRAVI

A.      (F/4)×(L/2)= FL/8

B.      (3/4 F)×(L/2)= 3/8 FL

C.      (5/4 F)×(L/2)= 5/8 FL

3-MOMENTO NEI RITTI

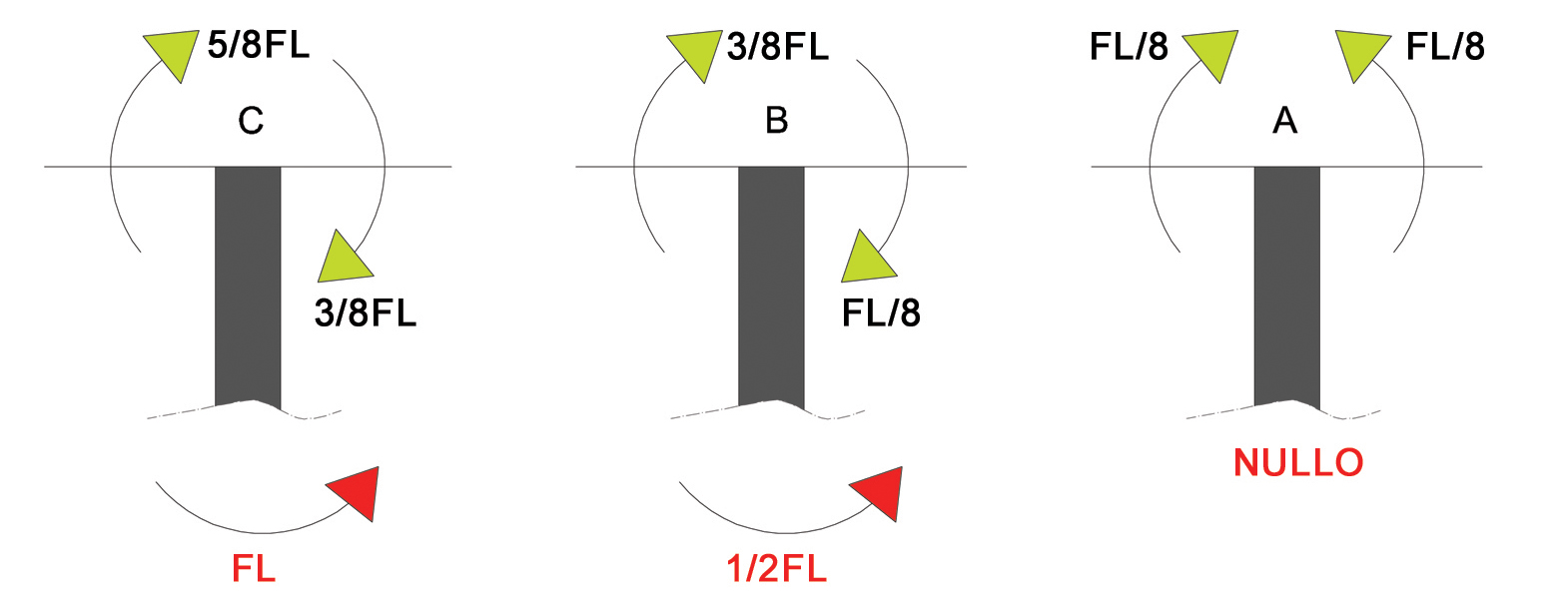
N.B: il momento nel ritto "A" è nullo per la considerazione di simmetria fatta all'inizio

A.      NULLO

B.      (FL/8) + (3FL/8)= 1/2 FL

C.      (3FL/8) + (5FL/8)=  FL

4-TAGLIO NEI RITTI

A.      NULLO

B.      [(1/2FL)+(1/2FL)]/2L= 1/2F

C.      [(FL)+(FL)]/2L= F

5-DIAGRAMMI

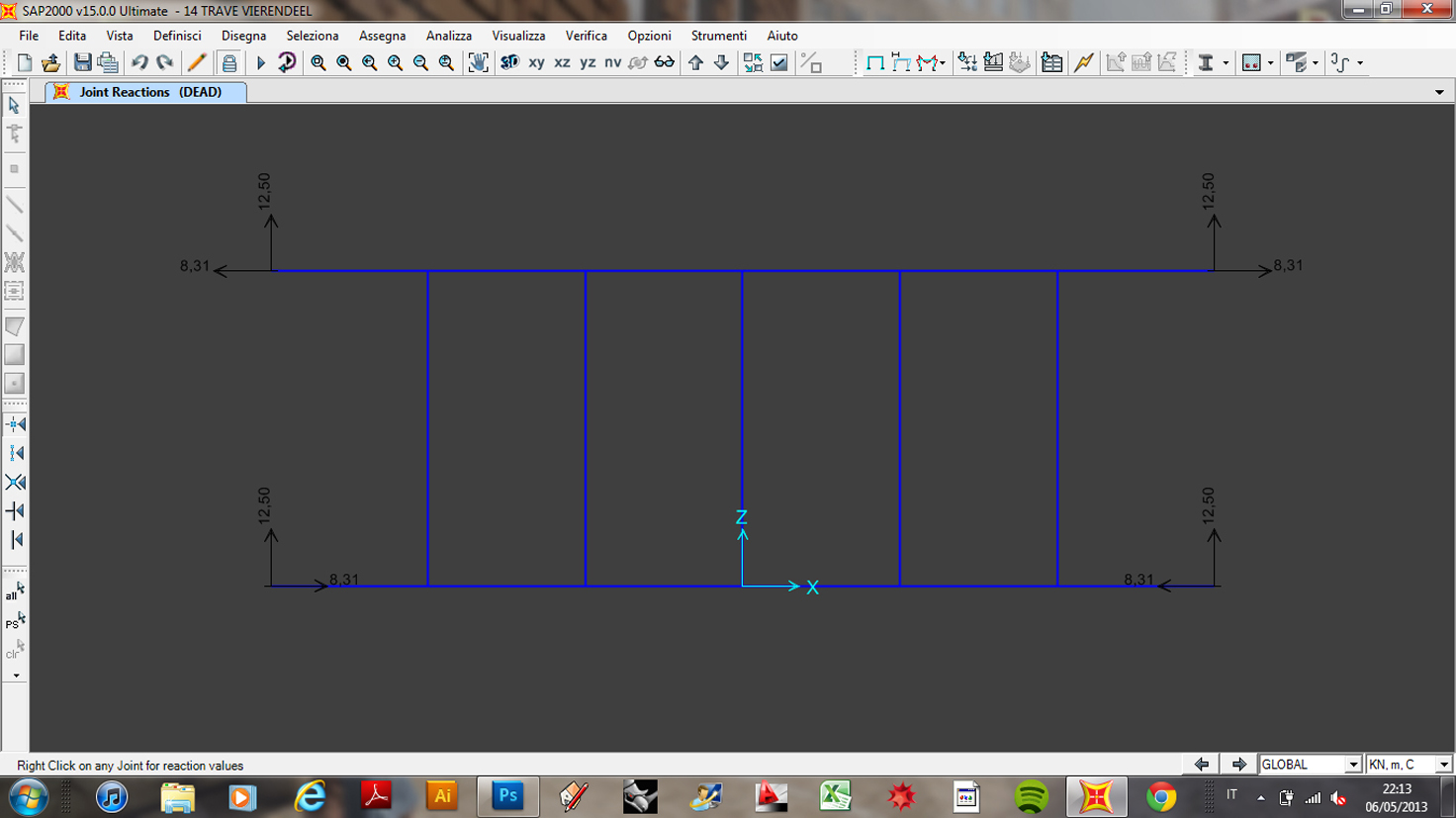
6-VERIFICA IN SAP

Qui sotto sono state riportate una serie di scatti fatti durante la risoluzione di una trave Virendeel doppiamente incastrata. F=10Kn, L(trave)=3m, L(ritto)=6m.

Ivalori ed i grafici delle sollecitazioni corrispondono perfettamente all'esercizio svolto a mano fatto salva qualche piccola divergenza dovuta a questioni di arrotondamento decimale!!!!