Esercitazione_Trave reticolare piana risolta con il metodo delle sezioni di Ritter

Risoluzione di una trave reticolare piana

Metodo delle sezioni di Ritter

Si ricercano I valori della normale a cui sono soggette le aste, tese o compresse, della struttura qui disegnata:

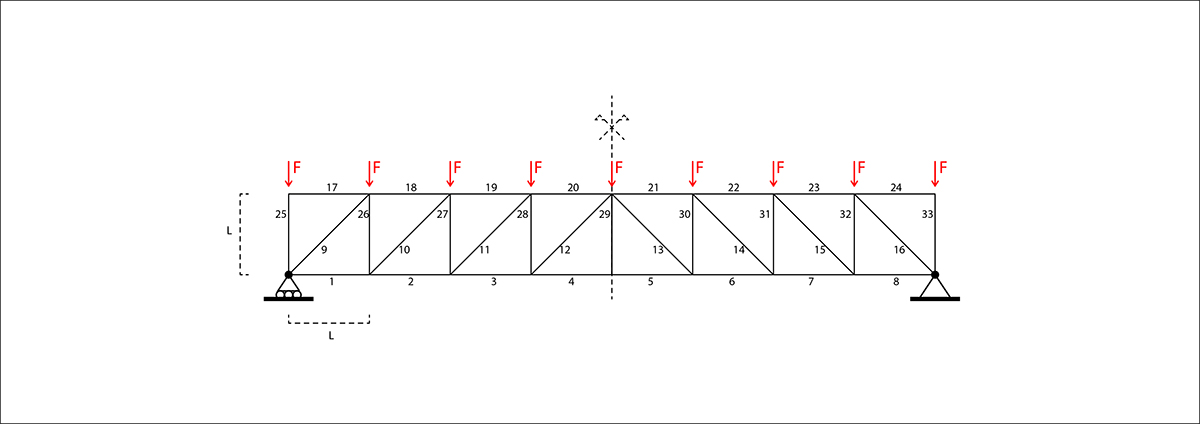
Essendo il sistema isostatico, si possono immediatamente  trovare le reazioni vincolari del carrello e della cerniera esterni.

Si procede quindi a ricercare le azioni di contatto delle aste interne con il metodo di Ritter. Tale metodo divide la struttura in due parti, sezionando tre aste per volta, analizzando le azioni di contatto che si liberano in conseguenza al distacco effettuato. 

Taglio 1

Eql. alla rotazione

M(A)= FL + N1L – (9/2)FL = 0

=> N1 = (7/2)F

Eql. delle forze verticali

sinN9– F + (9/2)F = 0

=> sinN9= -(7/2)F = cos N9

=> N9= (7/2) √2F

Eql. delle forze orizzontali

N17+ (7/2)F – (7/2)F = 0

=> N17= 0

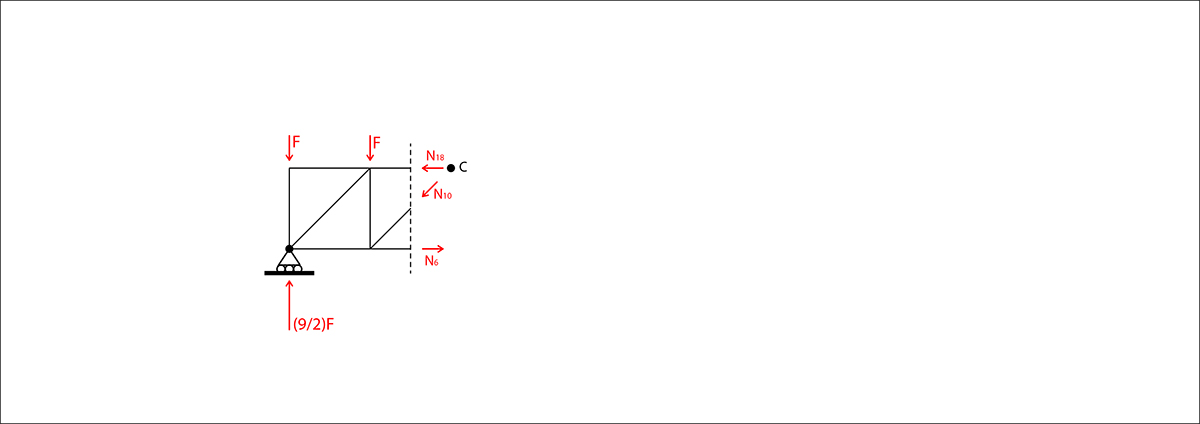
Taglio 2

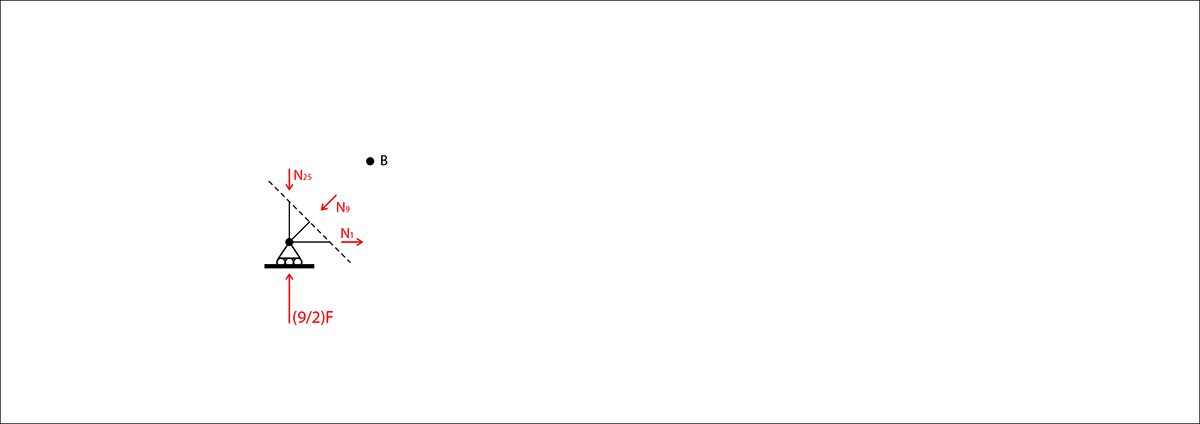
Eql. alla rotazione

M(a) = N25L – (9/2)FL + (7/2)FL = 0

=> N25= (9/2)F – (7/2)F = F

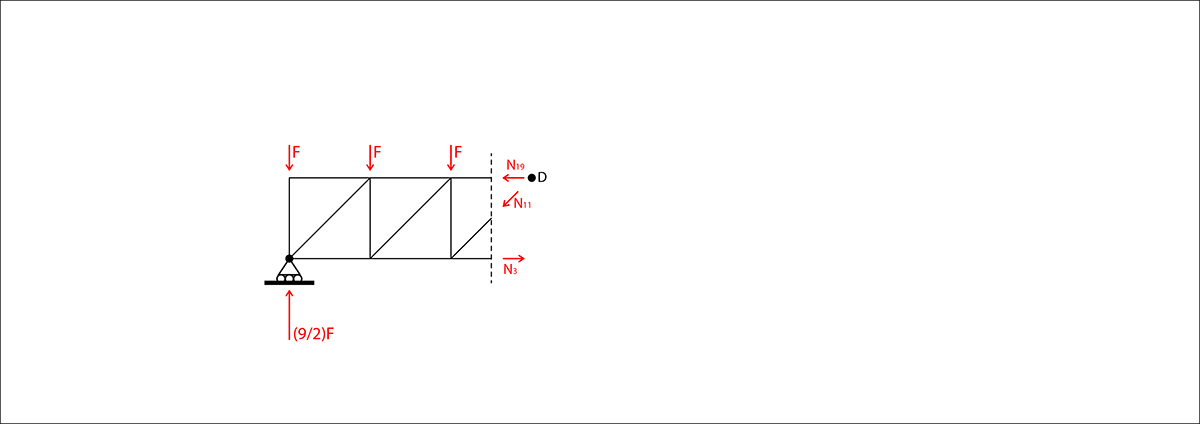
Taglio 3

Eql. delle forze verticali

- (9/2)F + 2F + sinN10= 0

=> sinN10= (9/2)F – 2F = (5/2)F  = cos N10

=> N10= (5/2)F √2

Eql. alla rotazione

M(C)= FL + F 2L – (9/2)F 2L + N2L = 0

=> N2= (9/2)F – 3F = (3/2)F

Taglio 4

Eql. delle forze verticali

sinN11+ 3F – (9/2)F = 0

=> sinN11= (3/2)F

=> N11= (3/2)F √2

Eql. alla rotazione

M(E)= N3L + 3F 2L – (9/2)F 3L = 0

=> N3= (15/2)F

Eql. delle forze orizzontali

N19+ (3/2)F – (15/2)F = 0

=> N19= 6F

Taglio 5

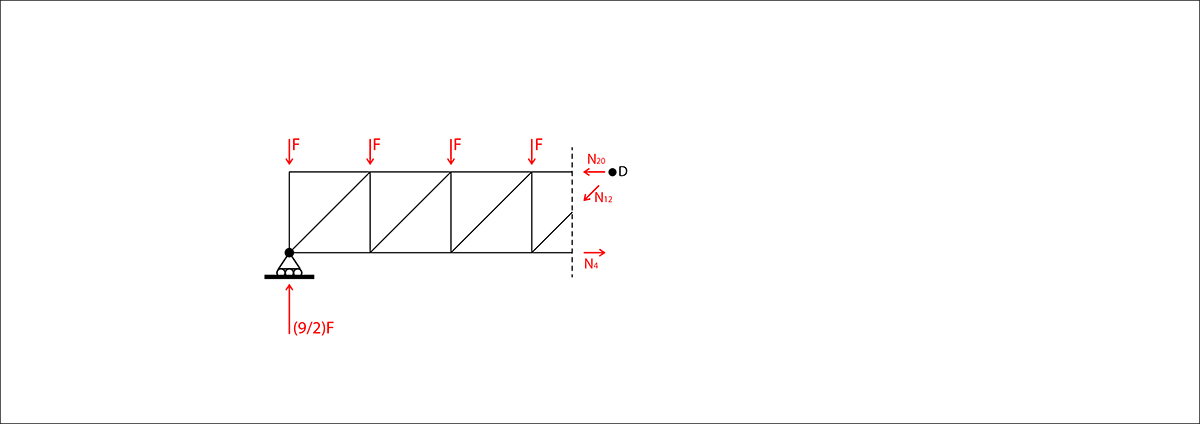
Eql. delle forze verticali

SinN12 + 4F – (9/2)F = 0

=> SinN12 = F/2

=> N12 = (√2/2)F

Eql. alla rotazione

M(G)= 4F 2L – (9/2)F 4L + N4L = 0

=> N4= 10F

Eql. delle forze orizzontali

N20 – 10F + F/2 = 0

=> N20 = (19/2)F

Per simmetria, le aste a queste simmetriche saranno soggette agli stessi valori delle azioni di contatto.

Trovati tali valori si può procedure all’individuazione delle aste tese e di quelle compresse:

Si può infine procedere a verificare l’esercizio modellando la struttura in SAP2000.

Vengono impostati, per semplicità di verifica rispetto ai calcoli manuali, una L = 1m e un carico applicator sui nodi di F = 10 KN

N.B. Trattandosi di una struttura reticolare in cui tutte le aste sono collegate da cerniere interne, si deve effettuare il rilascio del vincolo alla rotazione a tutte le aste.

Inoltre, dato che per il modello utilizzato consideriamo la struttura caricata solo di forze puntuali in corrispondenza dei nodi, dobbiamo eliminare dall’analisi il contributo del peso proprio della struttura, che costituirebbe per questa un carico distribuito sulle aste.

Si può quindi lanciare l'analisi dello sforzo normale (a destra una vista della deformata):

Si controllano i risultati ottenuti con quelli di calcolo a cui si sostituiscano i parametri con i carichi e le dimensioni stabilite.

Per verifica si controlli anche che le sollecitazioni di taglio e momento flettente siano nulle.