Esercitazione 8_Rigidezza Torsionale

Esercitazione 9

Rigidezza torsionale

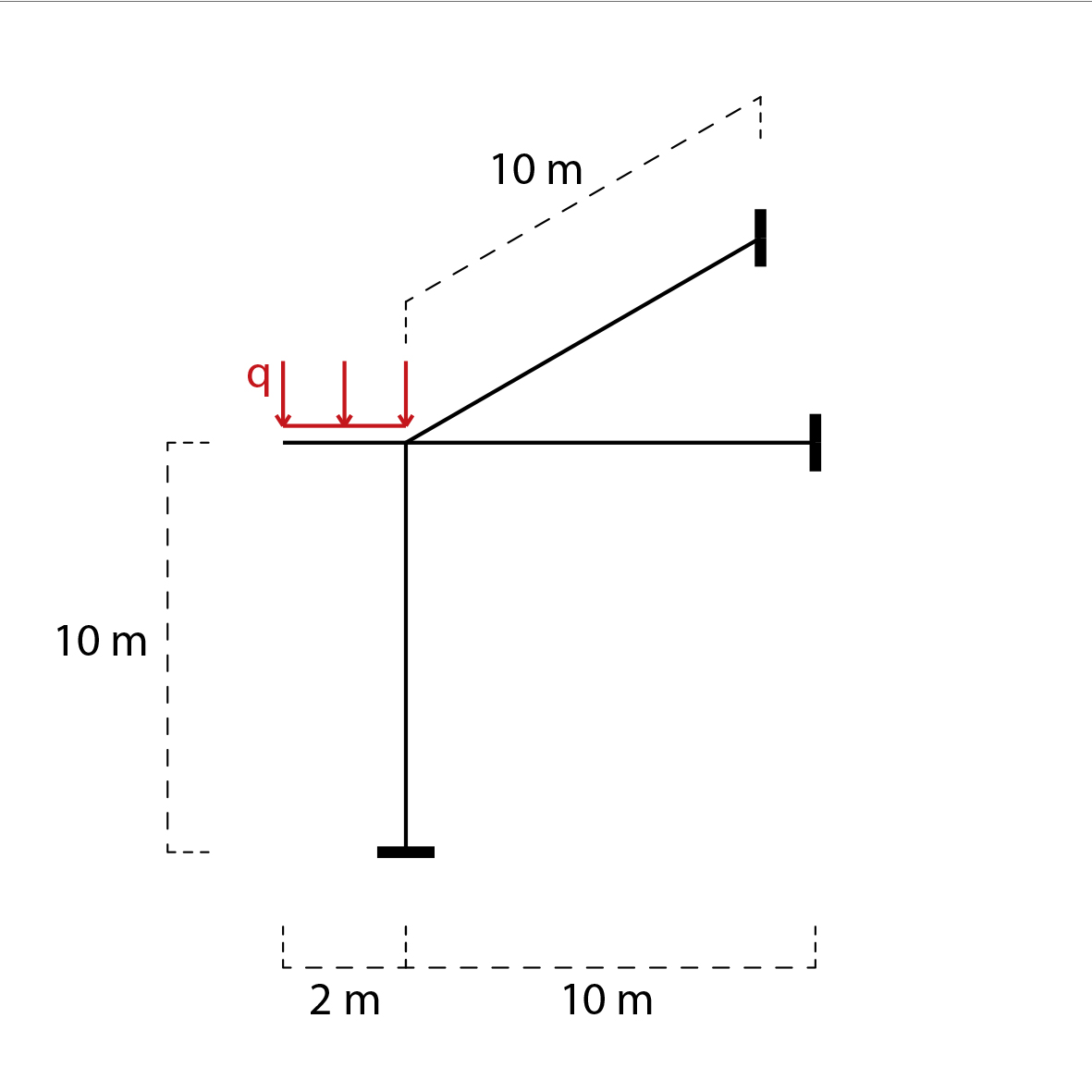
La struttura qui disegnata è soggetta ad un carico distribuito pari a 5 KN/m sul tratto a mensola. 

Tale carico provoca una deformazione di inflessione delle aste nel piano a cui lo stesso carico appartiene, ed una di torsione per l’asta a questo ortogonale. Ciò avviene perchè il nodo tra le travi è rigido (infatti, se si trascurano le deformazioni assiali, esso si muoverà di rotazione pura).

Come già anticipato, essendo il tratto caricato di tipo a mensola, la struttura può essere rappresentata con un sistema equivalente in cui la mensola ed il carico vengono sostituiti dal momento (5*2^2)/2 che questo genera.

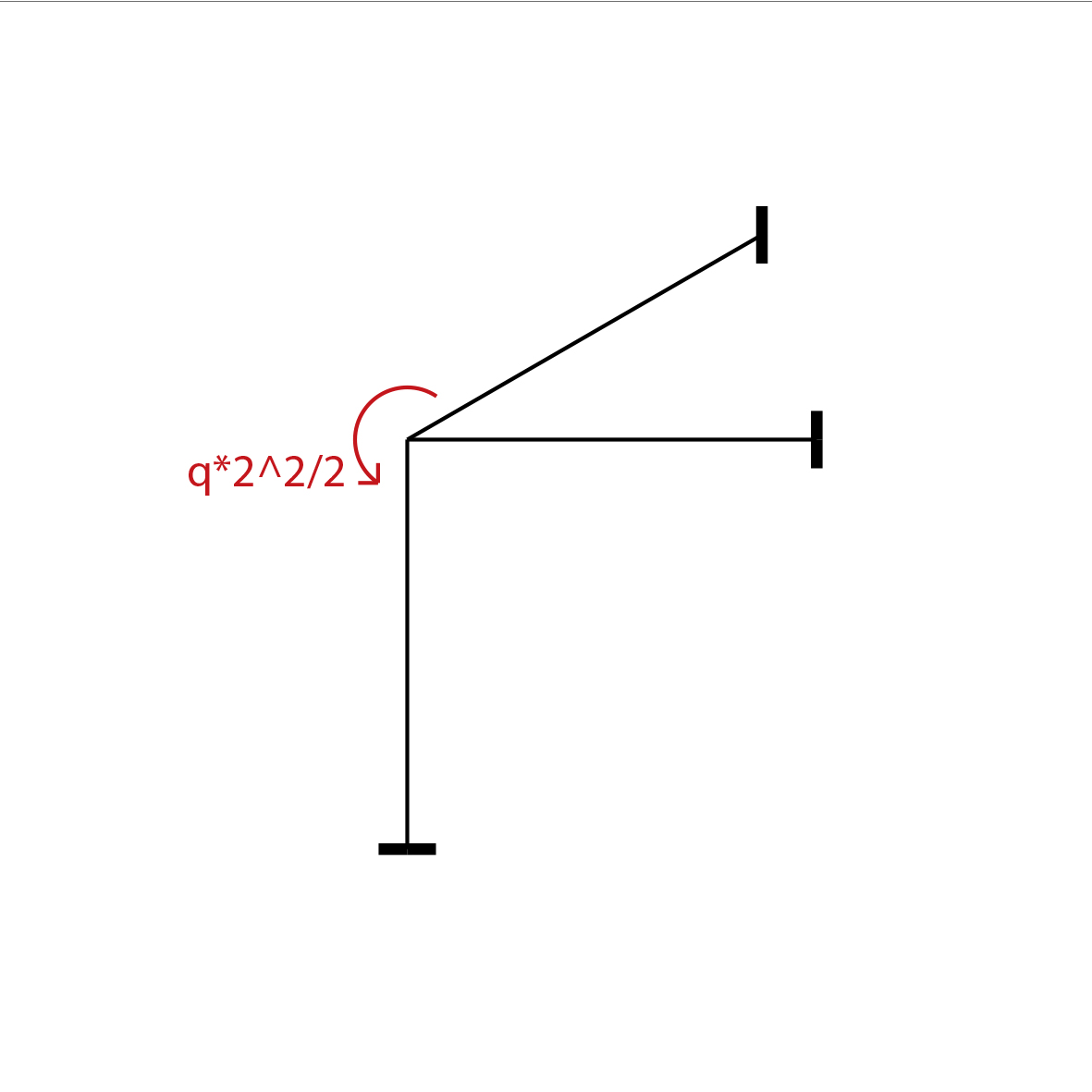
Questa rappresentazione aiuta ad intuire la natura qualitativa della conformazione deformata:

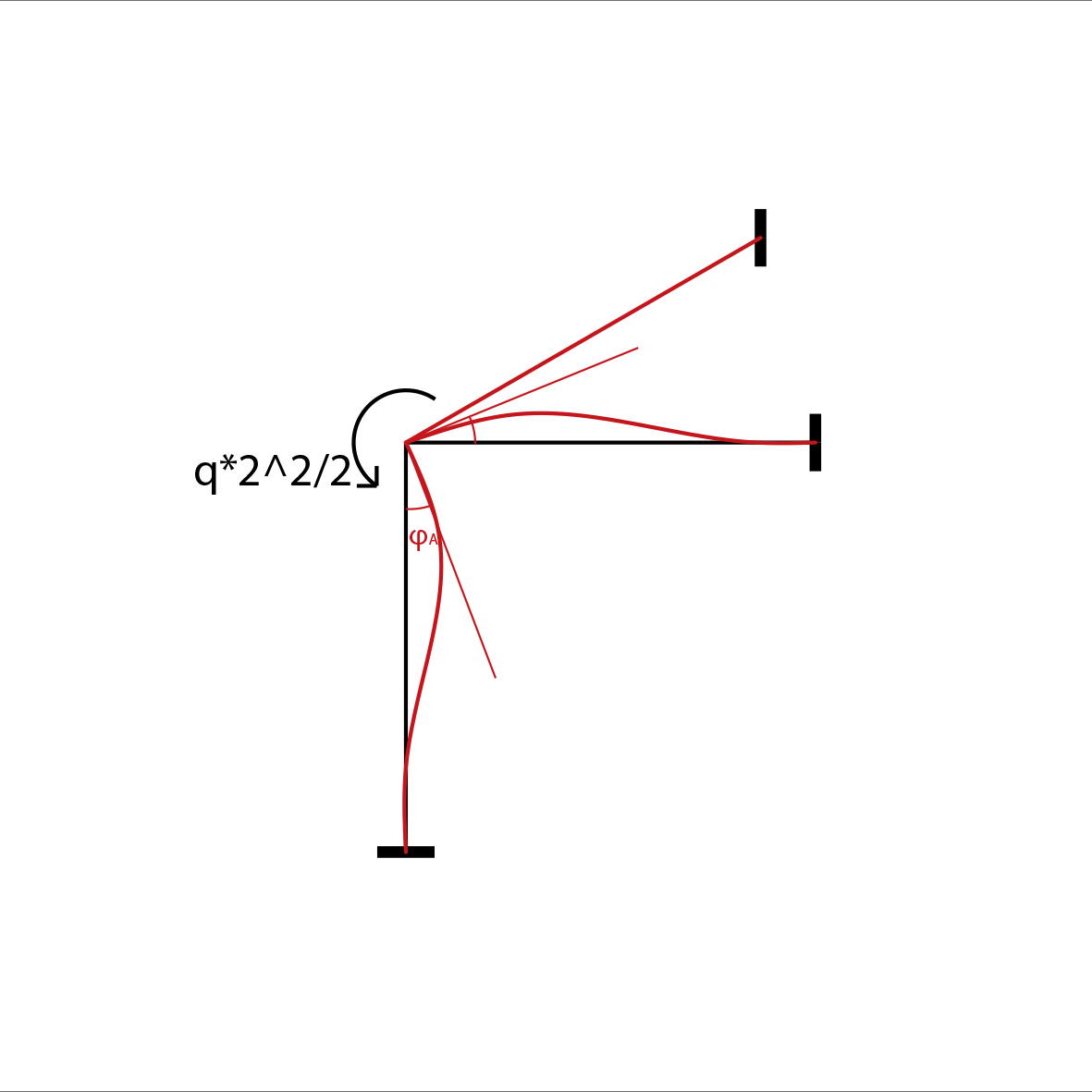
Il grafico dei momenti sarà noto per il metodo delle rigidezze:

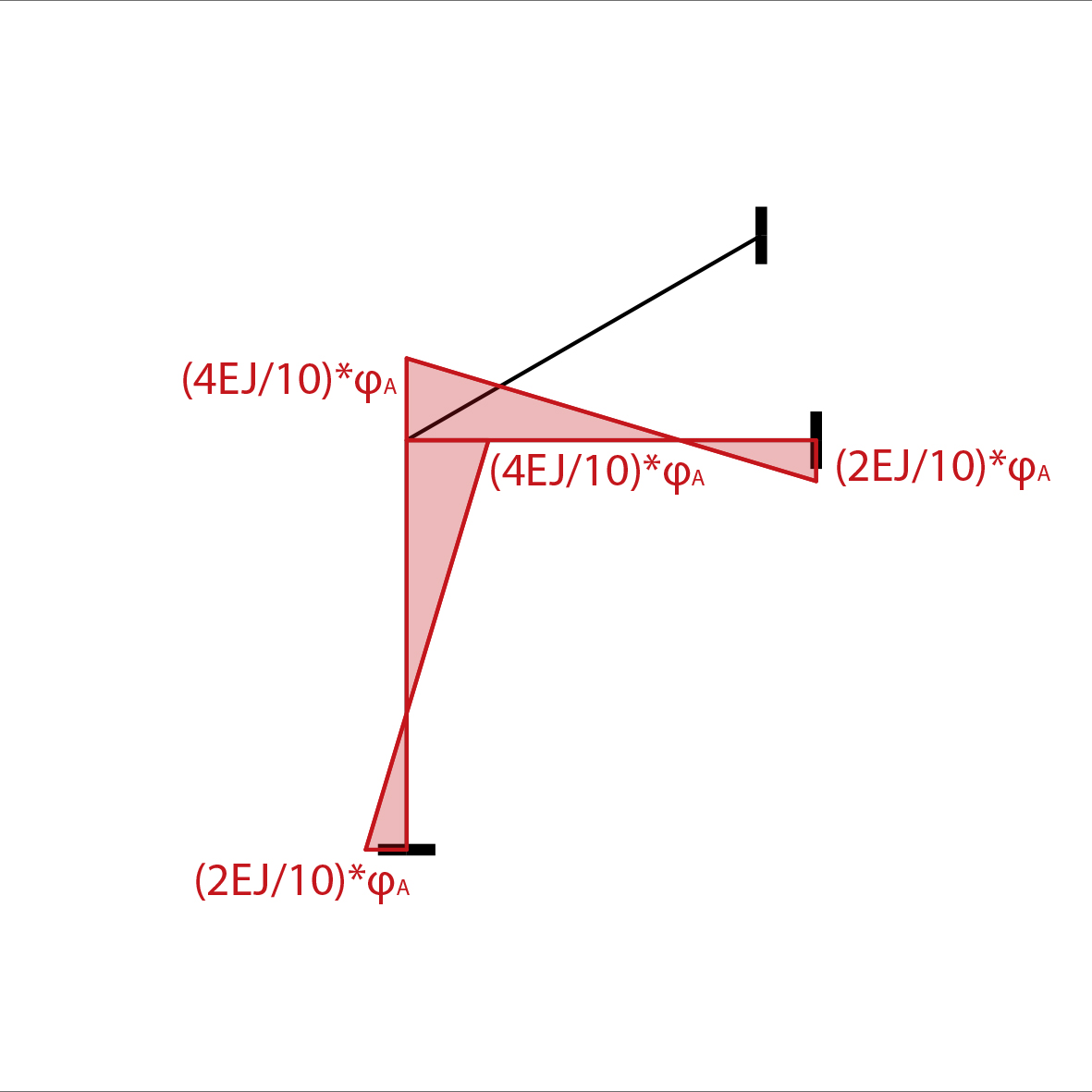
Possiamo così impostare l’equazione di equilibrio del nodo, nella quale l’unica incognita risulta essere la rotazione:

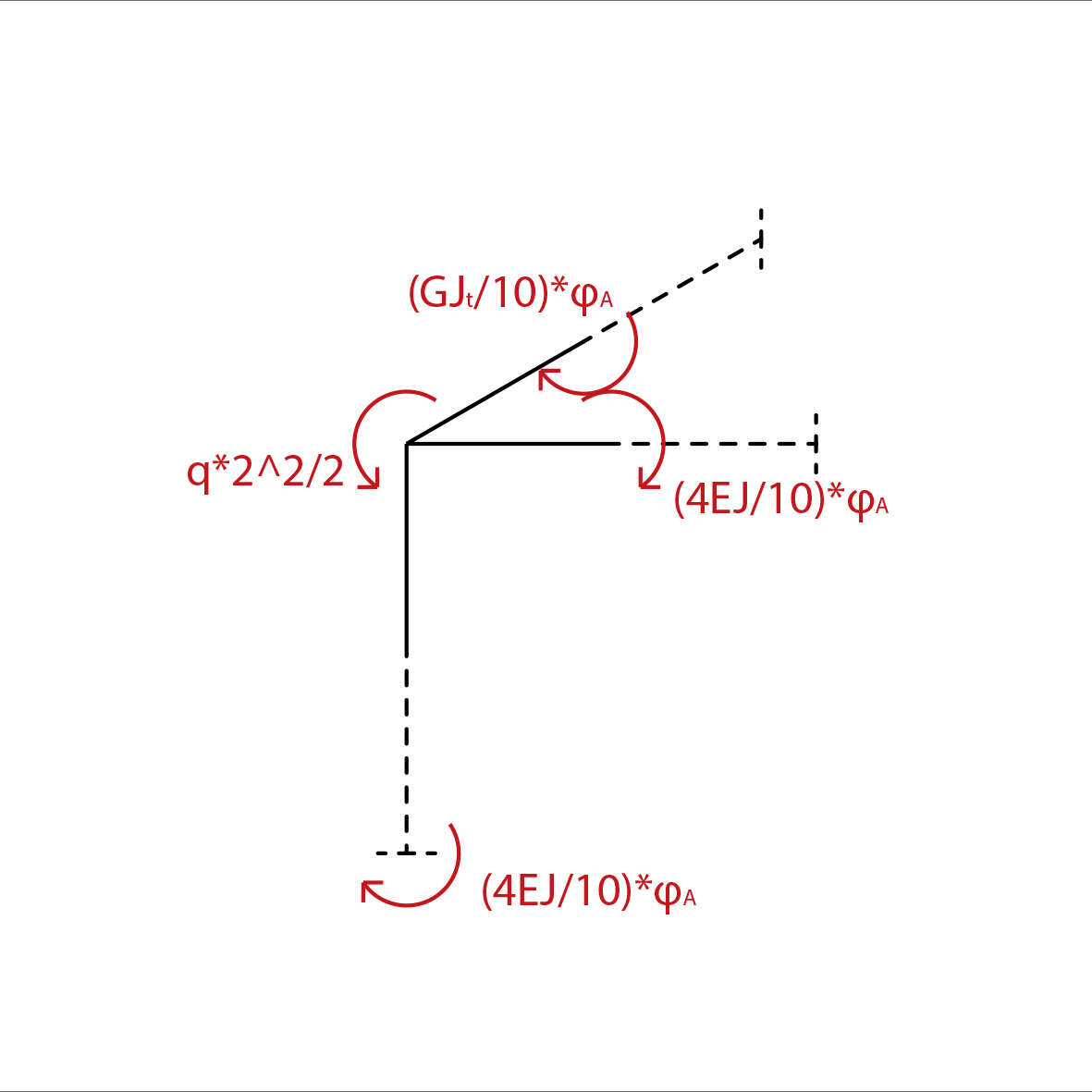
eql:

(5*2^2)/2 - (GJt/10)*φA - 2(4EJ/10)*φA = 0

=> φA = 100/(8EJ + GJt)

Per verificare l’influenza della forma della sezione sulla sua rigidezza torsionale, proviamo ad assegnare una sezione a tutte le aste, mantenendo fisse quelle delle aste soggette a flessione, cambiando di volta in volta la sezione dell’asta soggetta a torsione.

A quest’ultima verranno assegnate le seguenti sezioni:

1. C.A. rettangolare (0,67*0,15 m);
2. C.A. circolare (d = 0,36 m);
3. Scatolare quadrato acciaio (l = 0,2 m , t = 0,01 m);
4. Circolare cavo acciaio (d = 0,2 m . t = 0,01 m);
5. HE200.

Viene impostato un foglio excel per calcolare, una volta raccolti i dati derivanti dalla forma e dal materiale delle varie sezioni, la rotazione φA ed il momento torcente (che sarà proporzionale alla rigidezza torsionale della sezione).

1. C.A. rettangolare

1. C.A. circolare

1. Scatolare quadrato acciaio

1. Circolare cavo acciaio

1. HE200

N.B. Alcuni dati geometrici sono stati ricavati per comodità da SAP, nel menù section properties:

Ovviamente si può cercare un riscontro sulle ipotesi qualitative e quantitative fatte, tramite l’analisi della struttura su SAP.

In primo luogo si può verificare a livello qualitativo l’aspetto della deformata:

Mostro poi qui a titolo esplicativo il confronto tra la sezione circolare in C.A. ed il profilo scatolare quadrato.

C.A. circolare:

Scatolare quadrato:

Si può osservare, come già si intuiva, che le sezioni a profilo aperto hanno una rigidezza torsionale inferiore rispetto ai profili pieni o scatolari. Ovviamente influisce nella rigidezza anche la grandezza della sezione (le cui dimensioni appaiono nel modulo di rigidezza).

Come si è verificato con il metodo delle rigidezze nel caso della flessione, ad una maggiore rigidezza torsionale corrisponderà una maggiore sollecitazione di momento torcente (mentre inversamente proporzionale sarà ovviamente la deformazione).