OTTAVA ESERCITAZIONE: Rigidezza Torsionale

DESCRIZIONE:

Con questa esercitazione studieremo gli effetti che la torsione genera su un telaio iperstatico 3D e verificheremo, in seguito, attraverso SAP2000 , come varia la rigidezza torsionale di un telaio in base alle scelte progettuali che decideremo di adottare, quali il materiale e la sezione.

OSSERVAZIONI:

Qualsiasi forza esterna, che insiste sulla struttura, si ripartisce su di essa proporzionalmente alla rigidezza dei sui elementi, possiamo dire che il comportamento strutturale è un gioco di squadra dove il singolo ha un ruolo ben specifico ma il risultato finale che si considera è quello del gruppo!!!

Nell’analizzare questo telaio ci renderemo conto che il momento applicato, agente sul nodo 3D, viene trasmesso alla struttura in parte come momento flettente (asse y ed x), in parte in momento torcente (asse z).

Quindi, sul asse (z)  perpendicolare al piano (xy) dove agisce il momento esterno, l'effetto prodotto sarà una deformazione torcente della trave stessa, che reagirà  attraverso la sua rigidezza torsionale Rt che dipende da:

- modulo di elasticità tangenziale G

-  lunghezza l della trave

-  momento d'inerzia torsionale I_t.

La rigidezza torsionale Rt è:

-Rt=G ^. I_t / l

RISOLUZIONE:

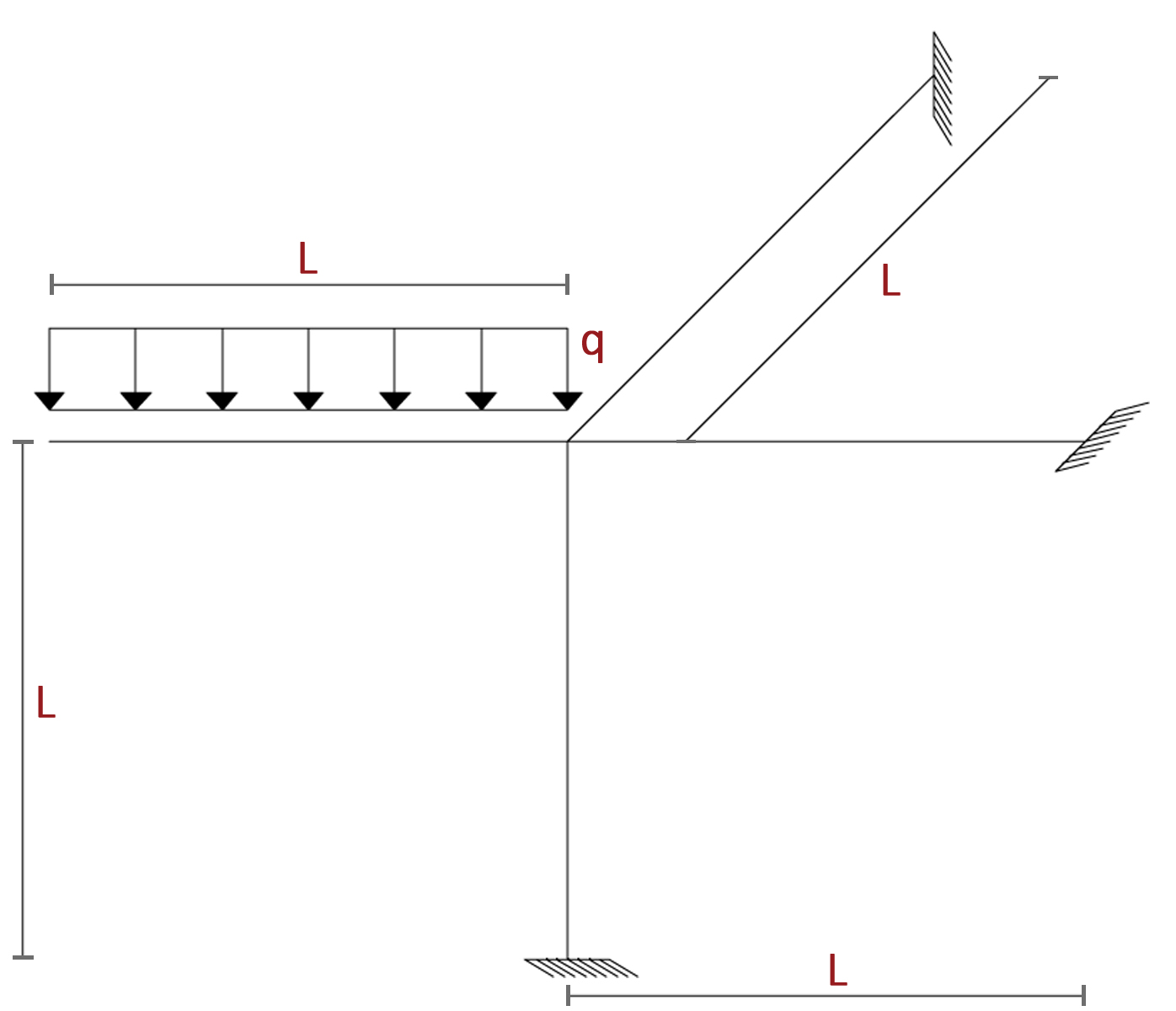
Il telaio in esame è composto da tre aste alle cui estremità sono presenti dei vincoli ad incastro ed un’asta a sbalzo sulla quale è presente un carico distribuito “q”. Tutte le aste hanno la stessa lunghezza pari ad “L”.

Il carico ripartito “q” genera un inflessione delle aste nel piano xy, ed una torsione dell’aste perpendicolare al piano xy.

La struttura complessivamente è iperstatica perche in 3D ogni incastro ha un numero di gradi di vincolo pari a 6 ed i g.d.l di un corpo sono 6, quindi la struttura è 12 volte iperstatica.

Lo sbalzo invece, preso singolarmente, risulta essere isostatico, quindi può essere risolto isolatamente.

Per risolvere l’esercitazione partiremo proprio risolvendo l'unico sisteme isostatico, lo sbalzo, cosicchè potremo avvalerci di un sistema equivalente dove saranno presenti nel nodo le sollecitazioni trasmesse alla struttura dallo sbalzo su cui insiste il carico ripartito “q” dove:

- il  corrispondente momento flettente vale ql²/2

- il carico verticale ql, che diventa sforzo normale sul pilastro, può essere trascurato in quanto la rigidezza assiale è maggiore rispetto a quella flessionale. => u_x=0 u_y=0 u_z=0

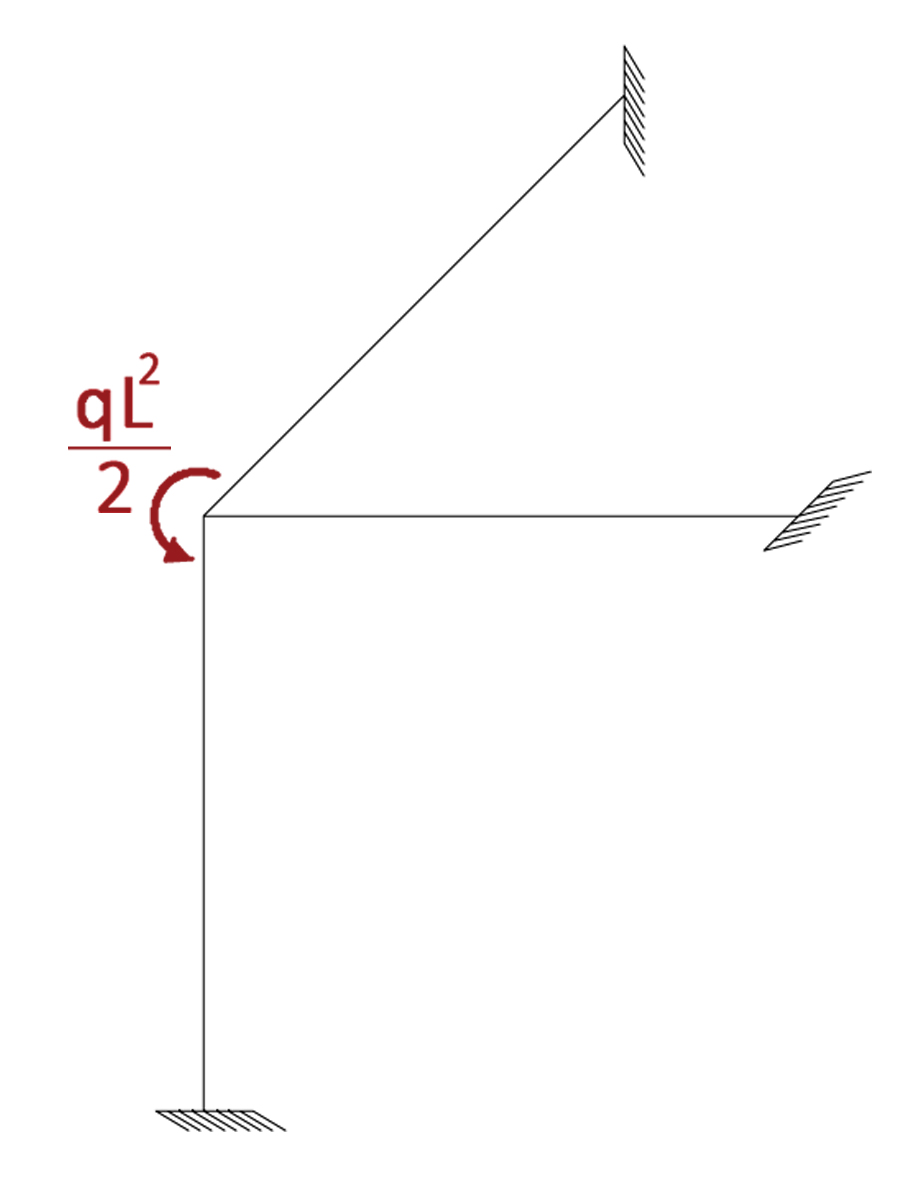
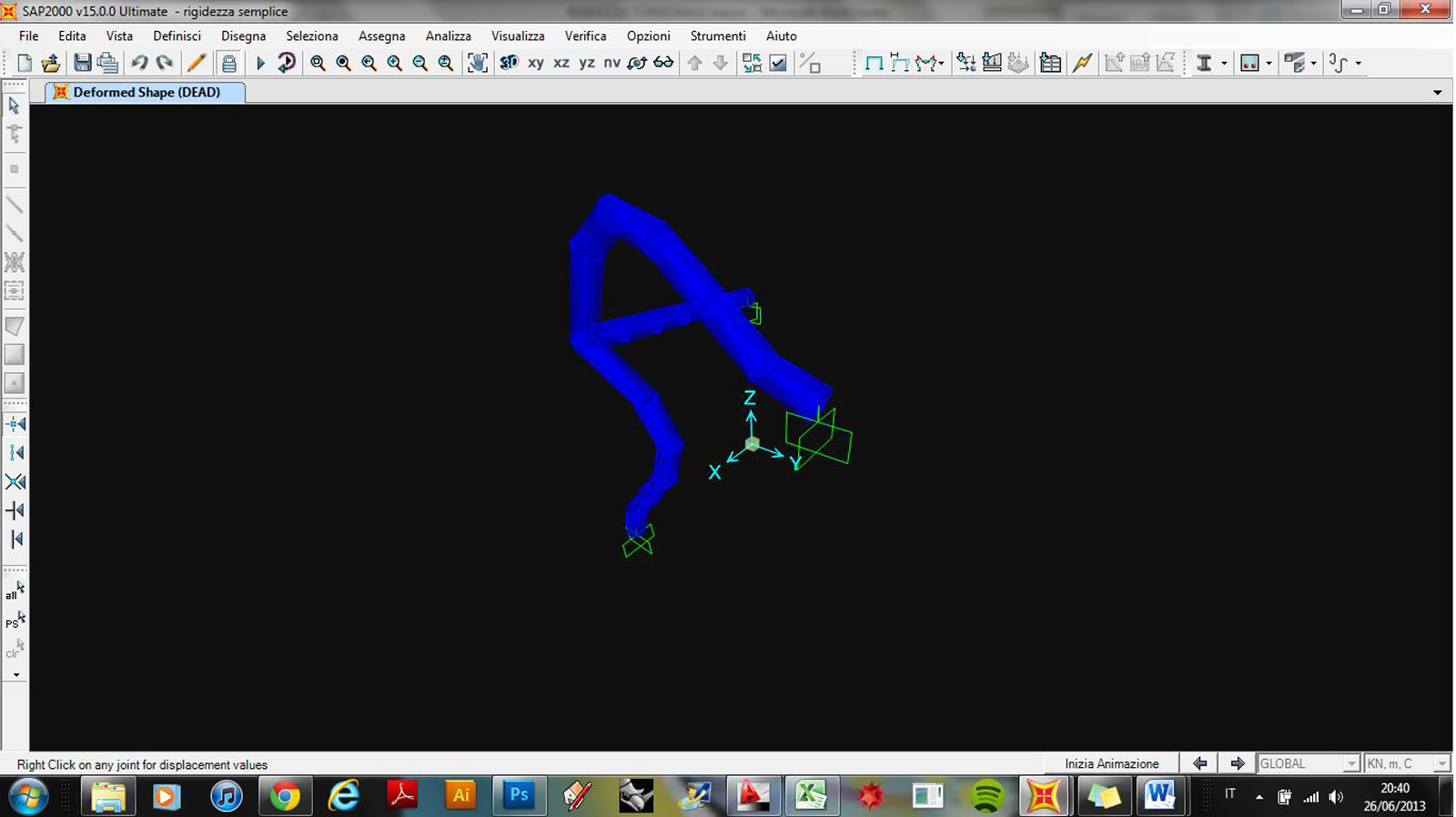
Sulla struttura, in conclusione agirà solamente un momento pari a ql²/2 che provocherà una rotazione φ_y; (unica incognita)

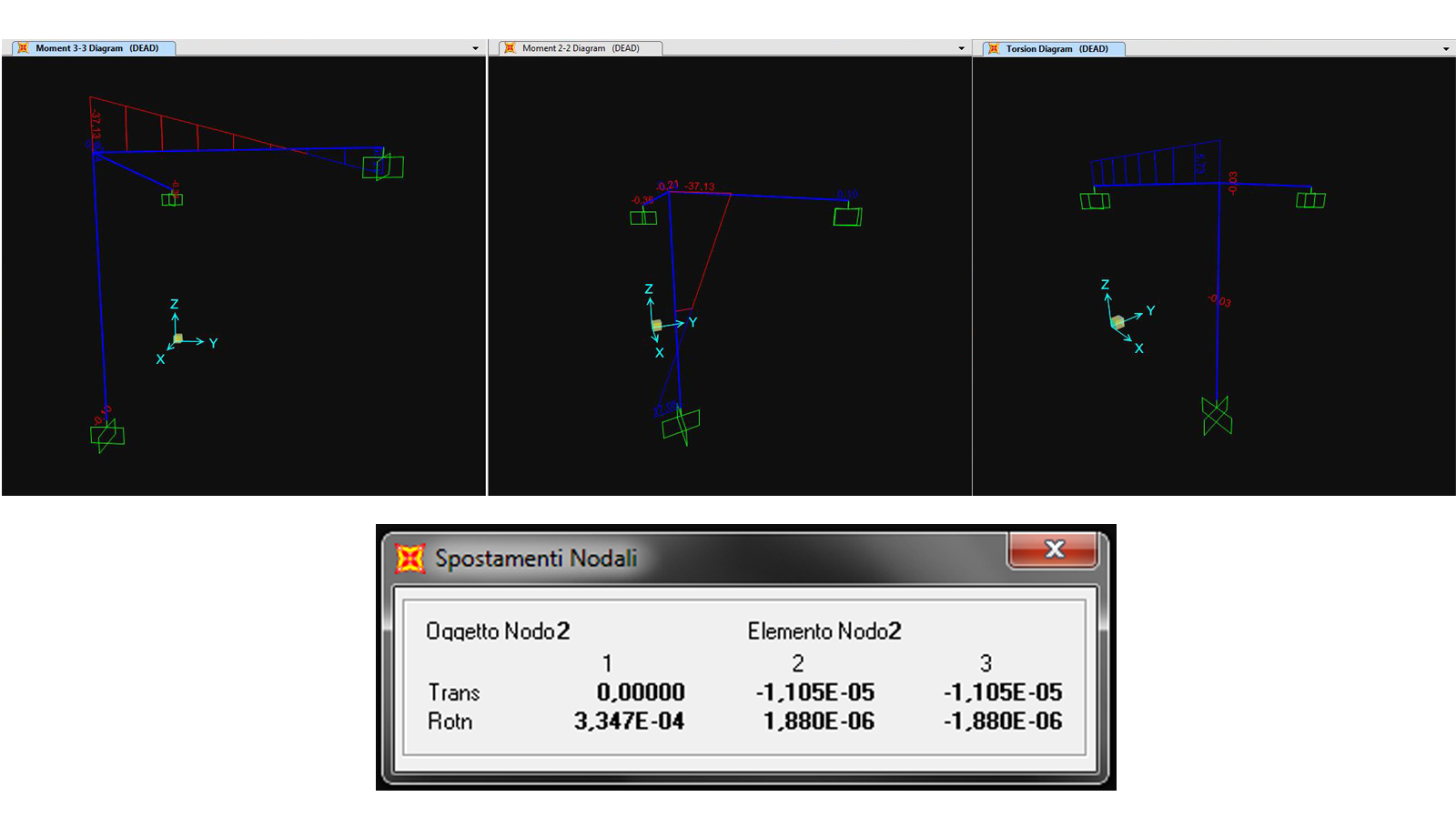
Di seguito sono riportati la graficizzazione della deformata ed il grafico dei momenti ricavati grazie allo schema noto del metodo delle rigidezze. (unica incognita)

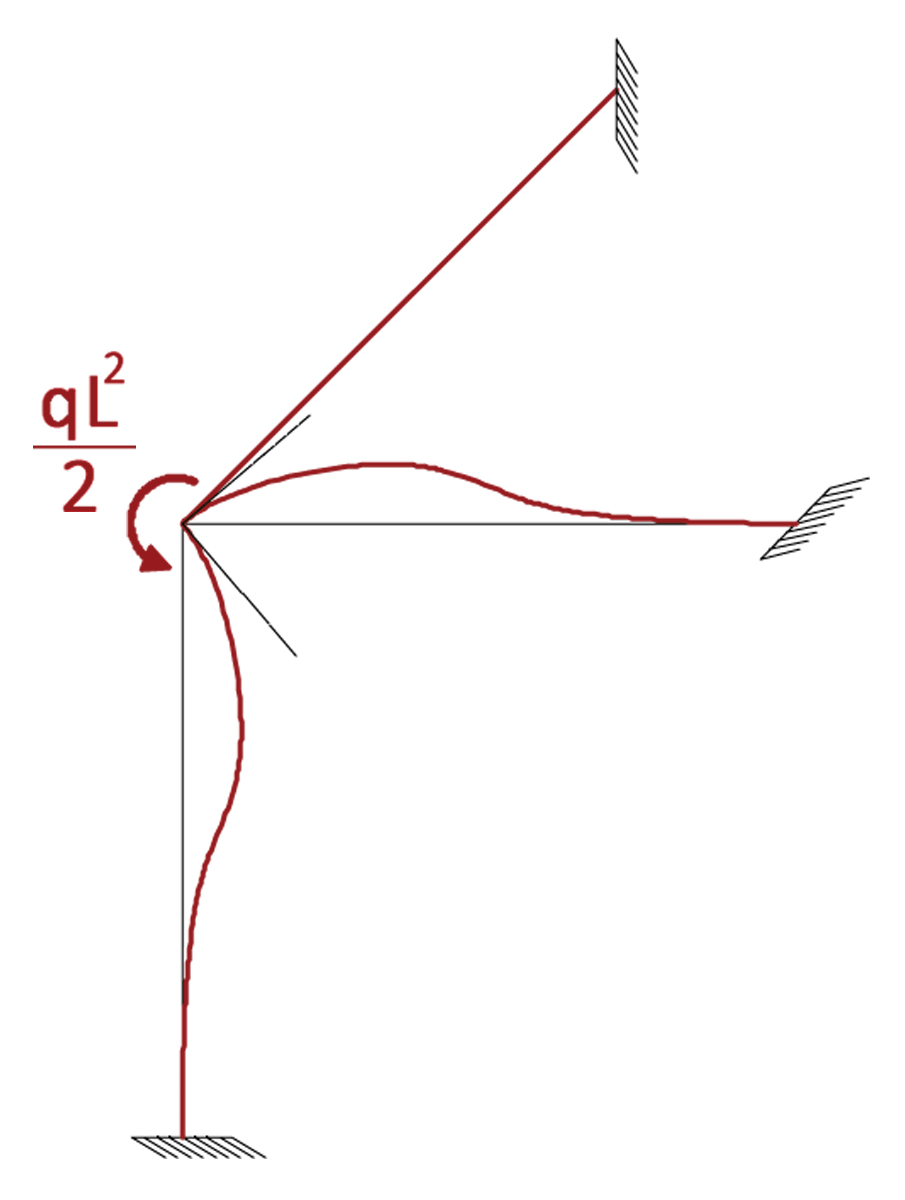
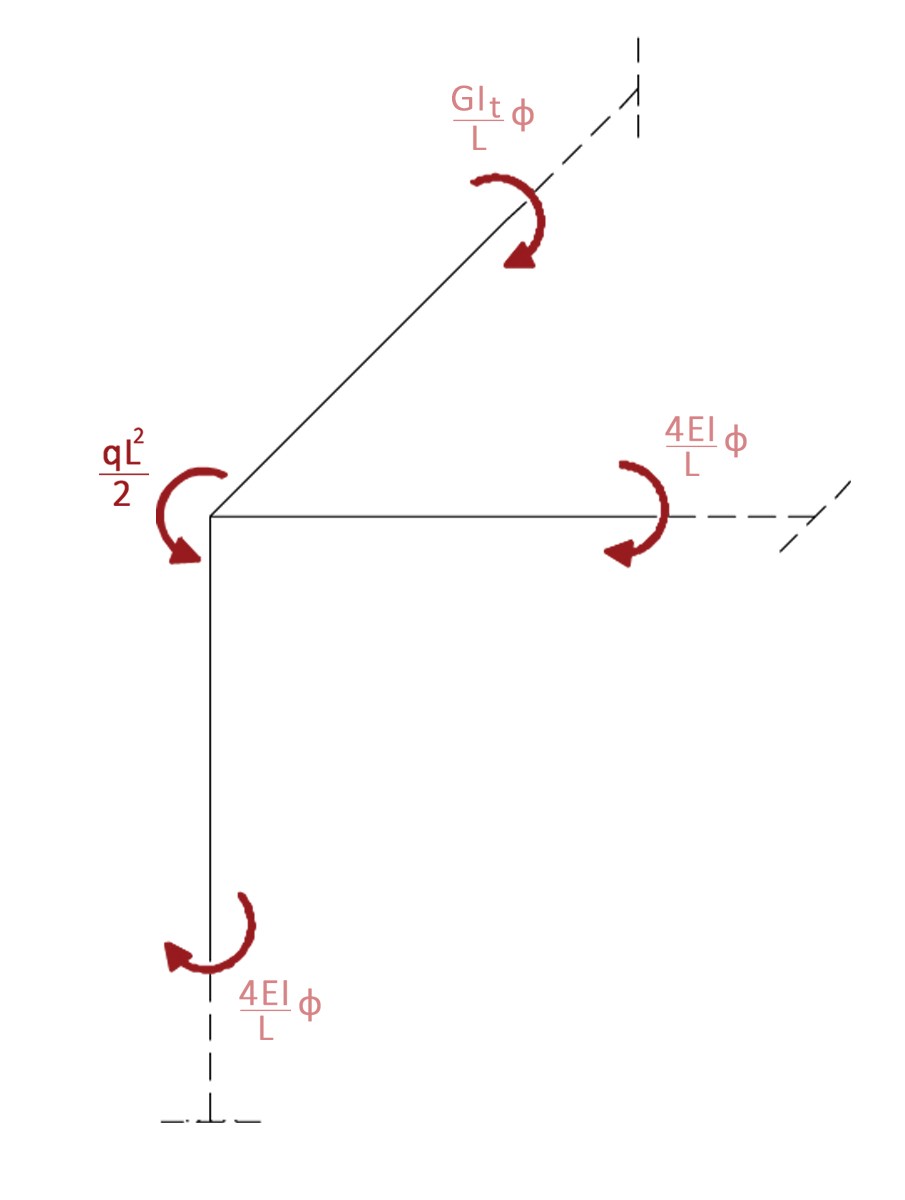
-Scriviamo l'equilibrio al nodo:

ql²/2 = (4EI/L+ 4EI/L + GI_t/L) φ con R= rigidezza del nodo= 4EI/L+ 4EI/L + GI_t/L

dunque:

- φ=ql²/2R  

- M=4EI(ql²)/L(2R)  

- M_t=GI_t(ql²)/L(2R)

VERIFICA IN SAP2000:

Analiziamo come varia la rigidezza torsionale di un telaio al variare del materiale e della geometria del materiale stesso....

N.B:La struttura sarà composta sempre da tre aste di lunghezza "L"=4m con un vincolo ad incastro alle loro estremità ed un asta a sbalzo, sempre di lunghezza "L"=4m, ed un carico ripartito "q"=10 KN/m che genera un momento "m",applicato sul nodo, pari a 80 KNm. 

CALCESTRUZZO:

1-sezione rettangolare 

I = momento d’inerzia = bh³/12 m⁴

E = modulo di elasticità = 21000 N/mm²=  21000000 KN/m²

G = modulo di elasticità tangenziale = 10000  N/mm²=  10000000 KN/m² 

I_t = coefficente di resistenza a torsione= c₂ x ab³ = (0,249)x(0,50)x(0,20)³ = 0,000996 m⁴

a/b è  tabellato. In questo caso vale a/b = 0.50/0.20 = 2,5 =>   c₂ = 0,249

2-sezione circolare 

I = momento d’inerzia = π x r⁴/64 = 0,001256m⁴

E = modulo di elasticità = 21000 N/mm²=  21000000 KN/m²

G = modulo di elasticità tangenziale = 10000  N/mm²=  10000000 KN/m² 

I_p = momento polare d'inerzia= π x r⁴/2 = 0,040192m⁴

ACCIAIO:

1-sezione scatolare

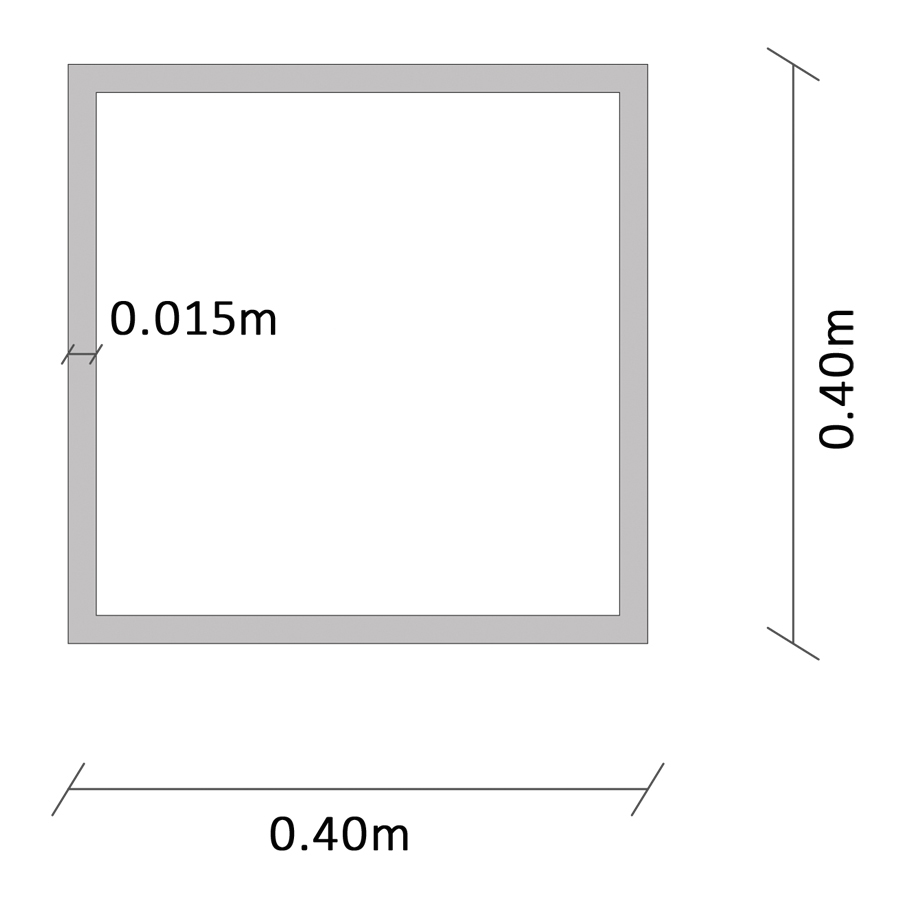
I = momento d’inerzia =0,0005715 m⁴

E = modulo di elasticità = 210000 N/mm²=  210000000 KN/m²

G = modulo di elasticità tangenziale = 80000  N/mm²=  80000000 KN/m² 

I_t = 0,000856 m⁴

2-IPE 270

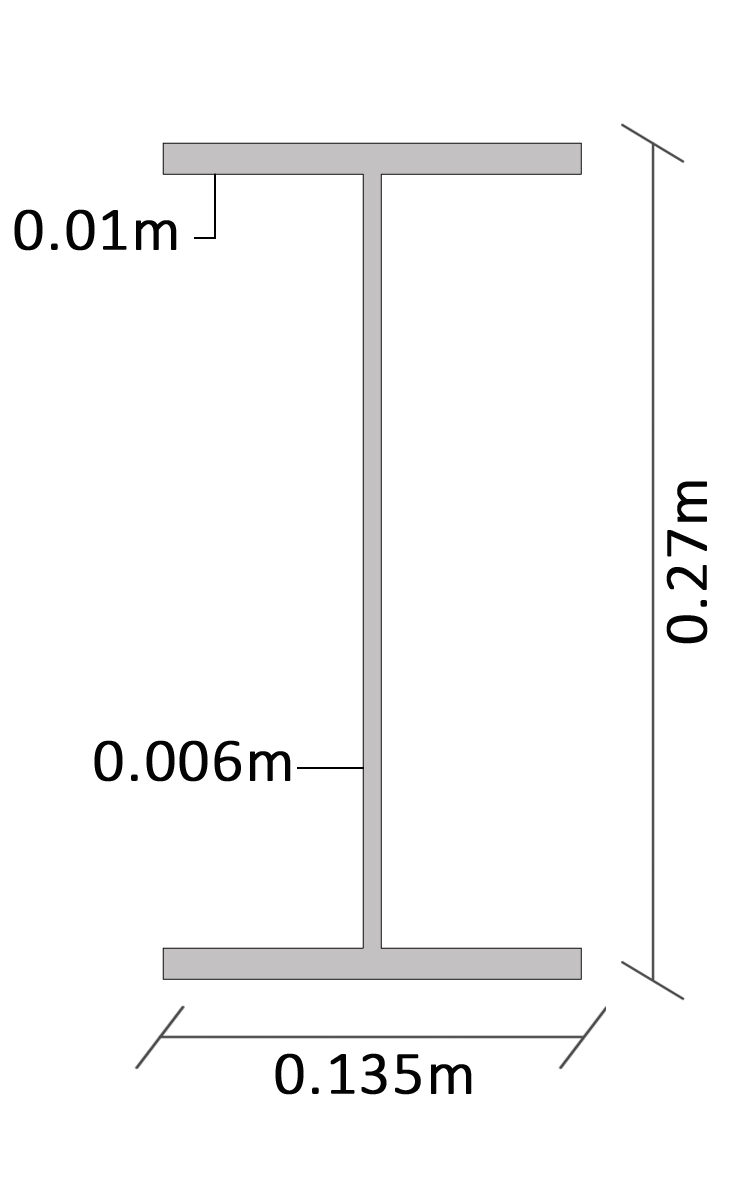
I = momento d’inerzia =0,0000542 m⁴

E = modulo di elasticità = 210000 N/mm²=  210000000 KN/m²

G = modulo di elasticità tangenziale = 80000  N/mm²=  80000000 KN/m² 

I_t = 0,00000011 m⁴

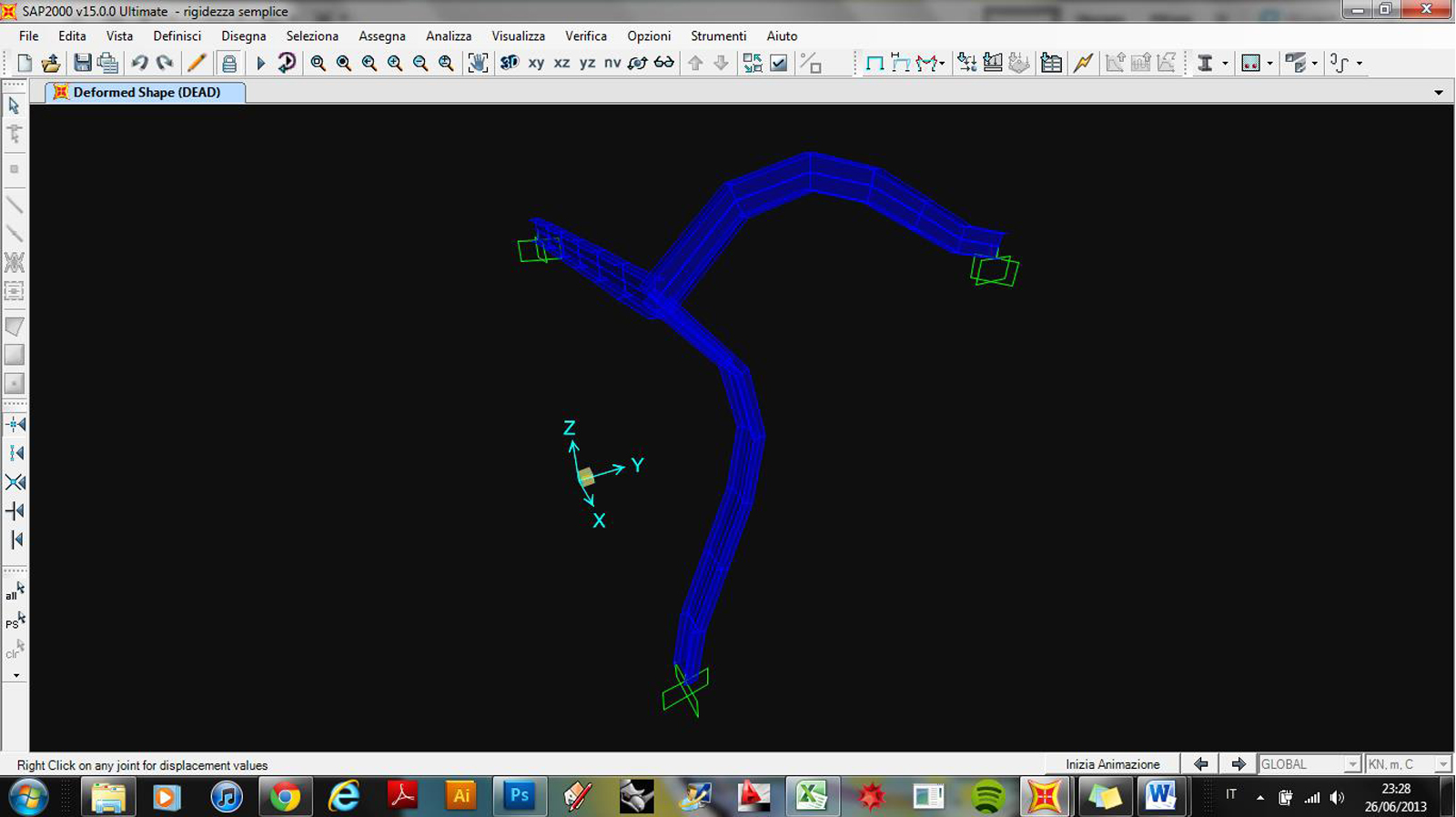
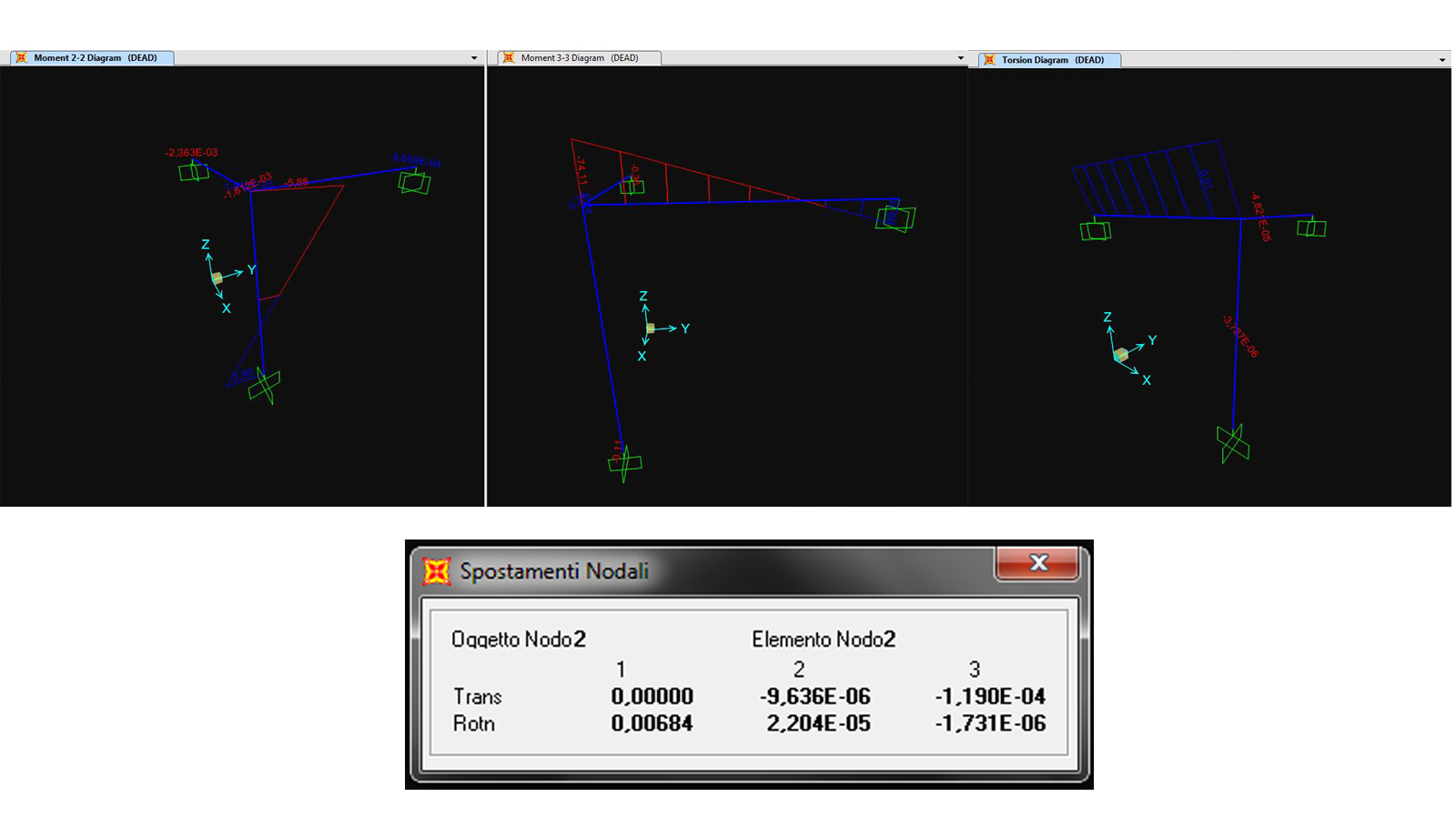
CONCLUSIONI:

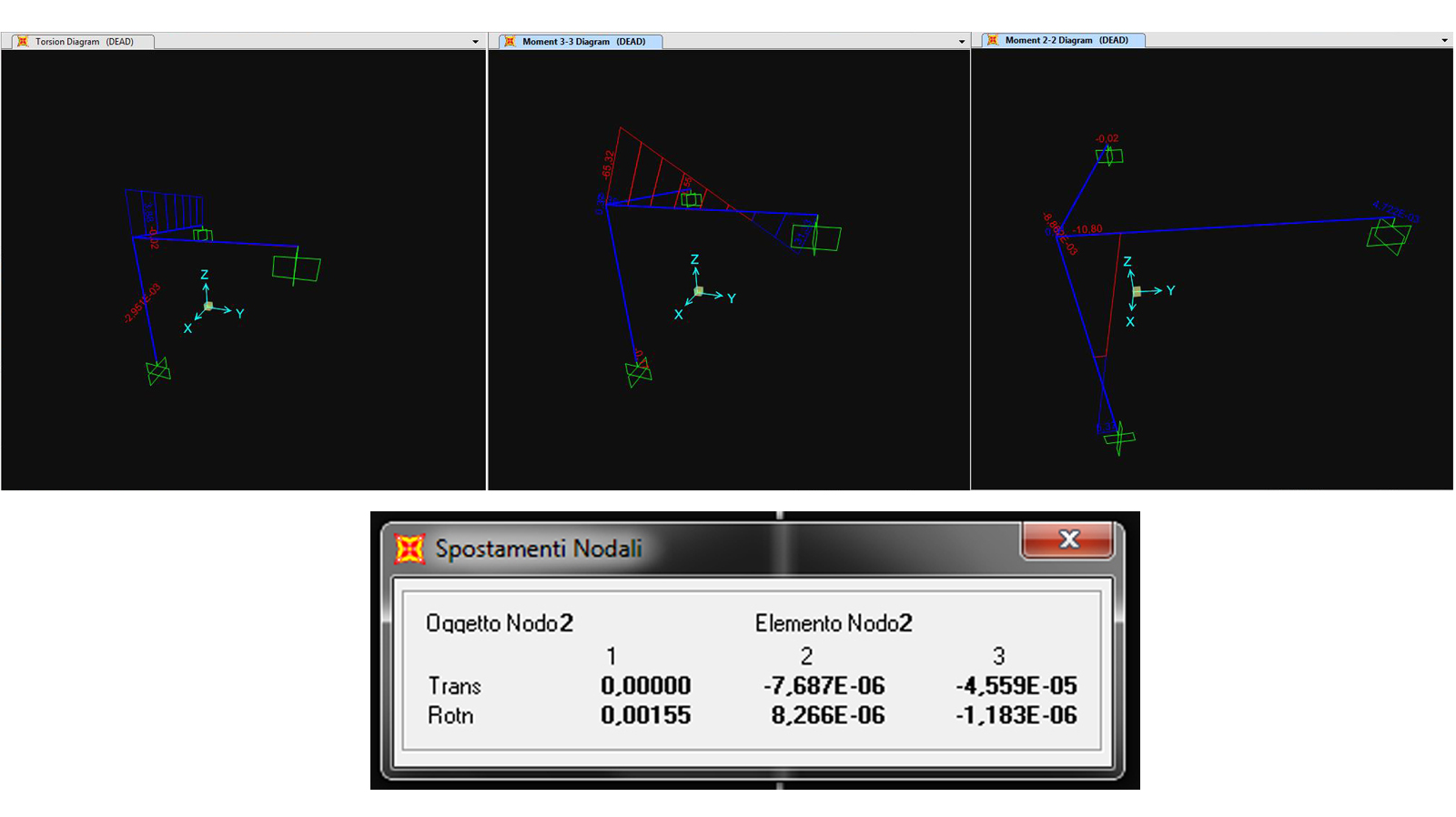
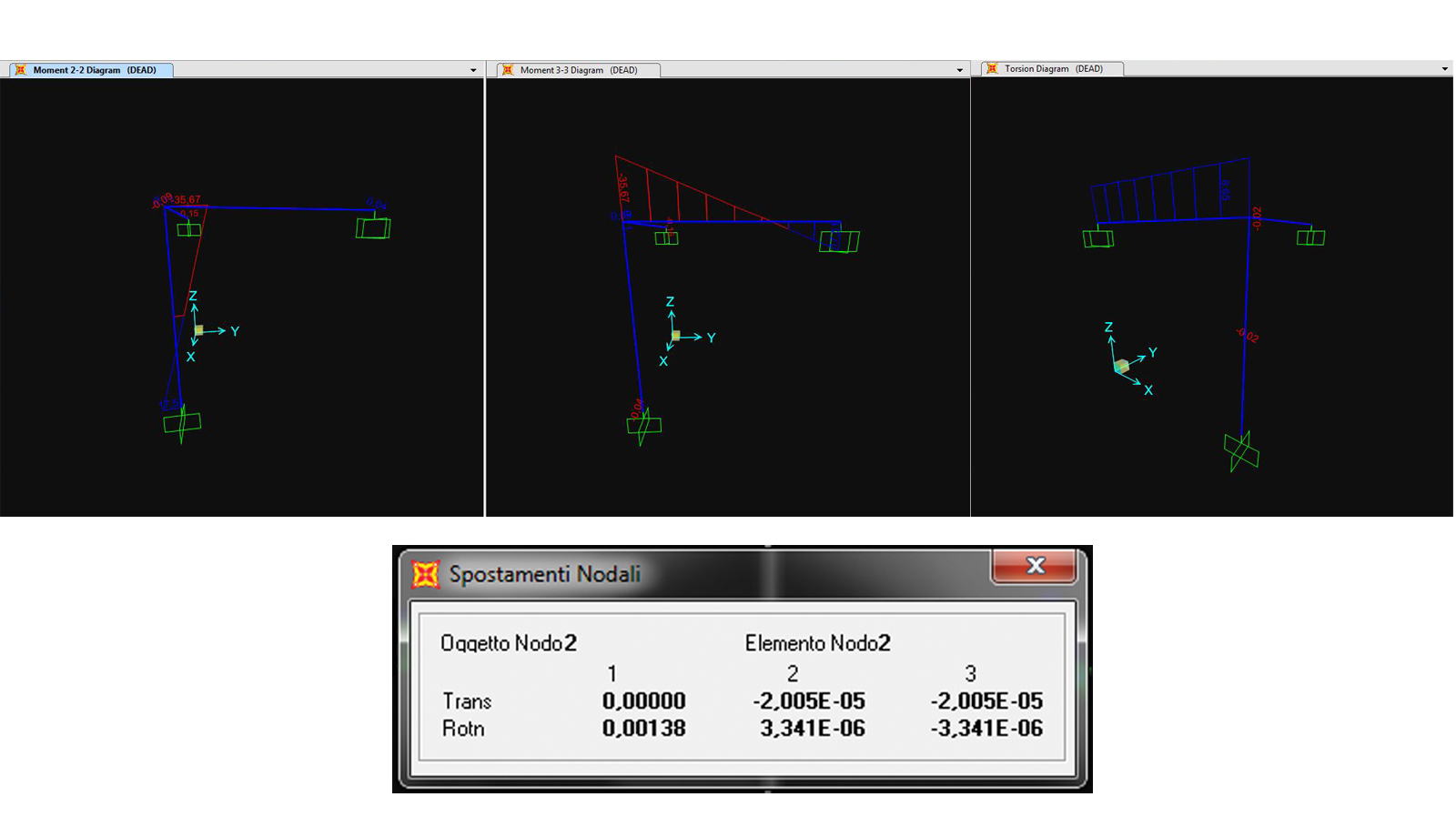
-sezione rettangolare in cls 0.2mX0.5m

M_t= 3,88 KNm      φ_y= 0,0000083

-sezione circolare in cls ø= 0.4m

M_t= 8,65 KNm      φ_y= 0,00000334

-sezione scatolare in acciaio 0.4mX0.4m s=0.0015m

M_t= 5,73 KNm      φ_y= 0,0000019

-IPE 270 in acciaio

M_t= 0,01 KNm      φ_y= 0,000022

Possiamo affermare che la geometria della sezione influisce notevolmente sulla Resistenza torsionale di un asta, ed in particolar modo le sezioni chiuse offrono resitenze torsionali maggiori rispetto alle sezioni aperte.

Importante, per questi fini, è anche il materiale: l'acciaio grazie al suo modulo di elasticità tangenziale offre più resistenza torsionale rispetto al cls che ha un modulo di elasticità tangenziale otto volte più piccolo.

Un asta con una rigidezza torsionale maggiore sarà in grado di supportare momenti torcenti maggiori e deformazioni più piccole rispetto un asta con una rigidezza torsionale inferiore.