Esercitazione 9_Graticcio di travi

Esercitazione 9

Graticcio di travi

Un graticcio di travi è un sistema strutturale in cui travi non parallele tra loro collaborano, in modo non gerarchico ma proporzionale alla propria rigidezza, all’equilibrio del sistema stesso. 

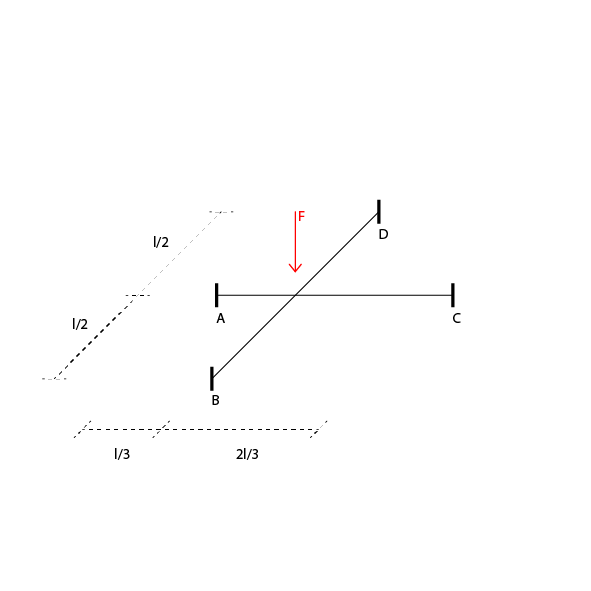
Esaminiamo in questa esercitazione in che modo le sollecitazioni dovute ad una forza F applicata nel nodo vengono spartite tra le travi.

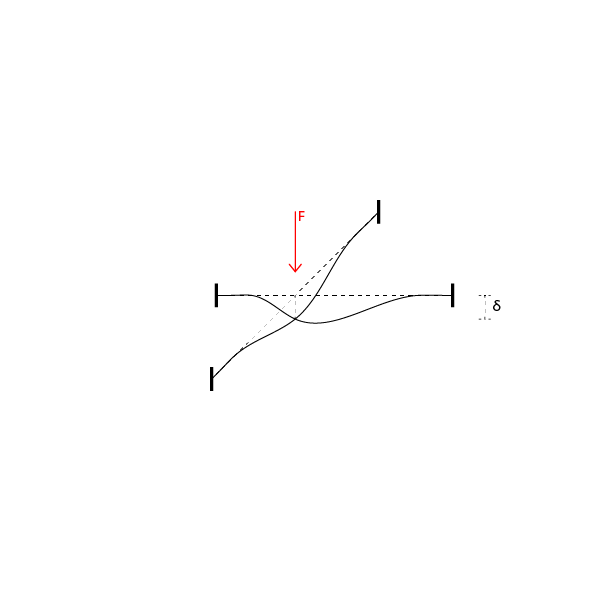
TRAVE A-C

Essendo la forza applicata ad l/3, nel punto di applicazione saranno diversi da 0 sia l’abbassamento δ che la rotazione φ. 

Possiamo quindi analizzare le deformazioni separatamente per poi fare uso del principio di sovrapposizione degli effetti. 

δ ≠ 0 ; φ = 0 .

φ ≠ 0 ; δ = 0 .

TRAVE B-D

In questa trave la forza è applicata a l/2, quindi nel punto di nullo del momento, per cui 

χ = 0. L’unica deformazione dovuta a F presente sarà quindi δ. 

Nondimeno, essendo il nodo un elemento rigido, la rotazione φ della sezione della trave A-C si presenta come torsione per l’elemento B-D. 

Sovrapponendo quindi tutti gli effetti dovuti ad F, possiamo procedere a scrivere le equazioni di equilibrio delle forze verticali e delle rotazioni.

eql. forze verticali

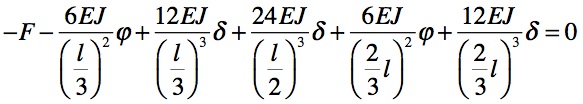
eql. rotazioni

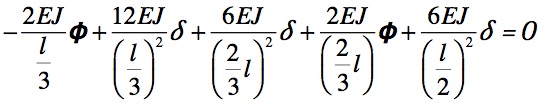
Mettendo a sistema le due equazioni si può giungere a trovare i valori di φ e di δ. 

Possiamo ora disegnare il sistema su SAP e analizzare la variazione dei valori delle sollecitazioni di momento flettente e torcente al variare della forma e della dimensione delle sezioni. Si useranno le stesse sezioni utilizzate nell'esercitazione precedente riguardante la rigidetta torsionale.

Acciaio_Circolare cava (d=0.36m;t=0.01m)

momento flettente

momento torcente

Acciaio_tubolare a sezione quadrata (l=0.2m;t=0.01)

momento flettente

momento torcente

Acciaio_IPE300

momento flettente

momento torcente

c.a._rettangolare (0.67*0.15m)

momento flettente

momento torcente

c.a._circolare (d=0.36m)

momento flettente

momento torcente