GRATICCIO DI TRAVI
Si chiama graticcio una struttura dove c’è una collaborazione tra due sistemi di travi più o meno ortogonali tra loro senza alcuna gerarchia, infatti l’intero sistema ha lo stesso momento d’inerzia (cioè i due sistemi di travi hanno la stessa sezione e stesso materiale) e i nodi sono tutti incastri che permettono il passaggio di momento e quindi il ripristino della continuità della trave.
Come già studiato nell’esercizio sulla rigidezza torsionale, anche nel graticcio questa entra in gioco grazie alla flessione di alcune aste che provocano una torsione nella direzione a loro ortogonale.
La struttura analizzata è un graticcio semplice formato da due travi di lunghezza pari a 6m ortogonali tra loro e incastrate nell’asta BD nel punto di mezzeria, mentre nell’asta AC a 1/3 della lunghezza, con una forza F=10 KN applicata sul nodo centrale .
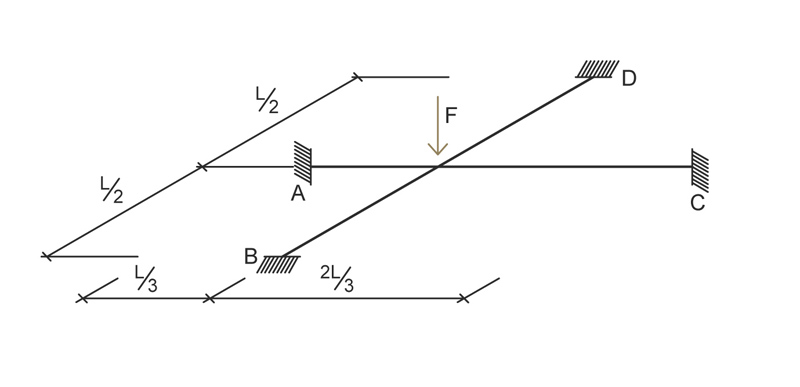
Se conosciamo gli spostamenti del nodo libero allora conosciamo anche quelli delle aste.
Trovandoci nello spazio tridimensionale, il nodo ha 6 gradi di libertà, esso può traslare e ruotare nelle direzioni x, y, z, ma per i vincoli che ci siamo dati sappiamo che in x e y il nodo non può traslare orizzontalmente altrimenti le aste si accorciano ed allungano, quindi è possibile il solo abbassamento .
La rotazione attorno a z non ci sta perché non ci sono forze applicate, mentre abbiamo una rotazione attorno a y in quanto nell’asta AC la forza non è applicata al centro ma ad 1/3 quindi la tangente alla deformata non è orizzontale. Le incognite di spostamento che abbiamo sono due ,
Con il metodo della sovrapposizione degli effetti possiamo studiare come la struttura reagisce ai nostri due parametri di spostamento facendoli agire uno per volta.
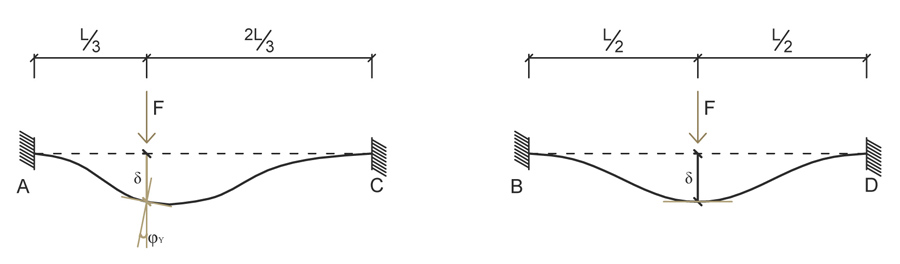
Facciamo agire solo l’abbassamento
Grazie agli schemi notevoli di una trave doppiamente incastrata possiamo ricavarci i valori di taglio e momento flettente.
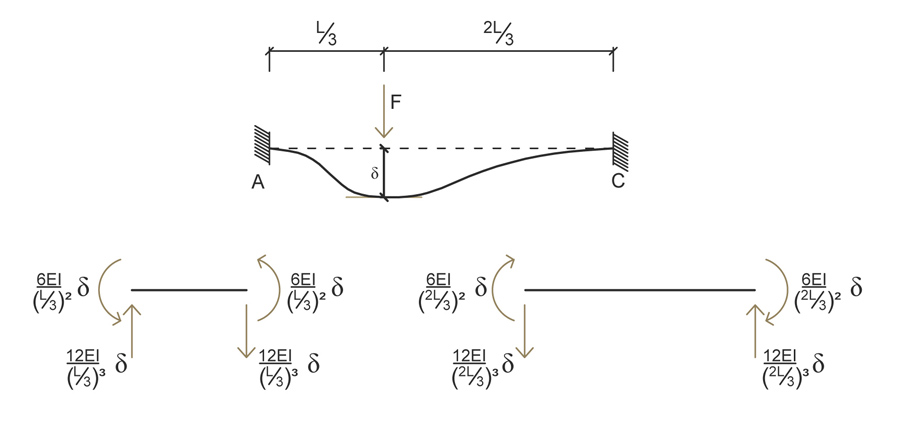
Nell’asta BD i due momenti sono uguali e contrari e si annullano, infatti questi riguardano una eventuale rotazione attorno all’asse x che in questo caso non abbiamo.
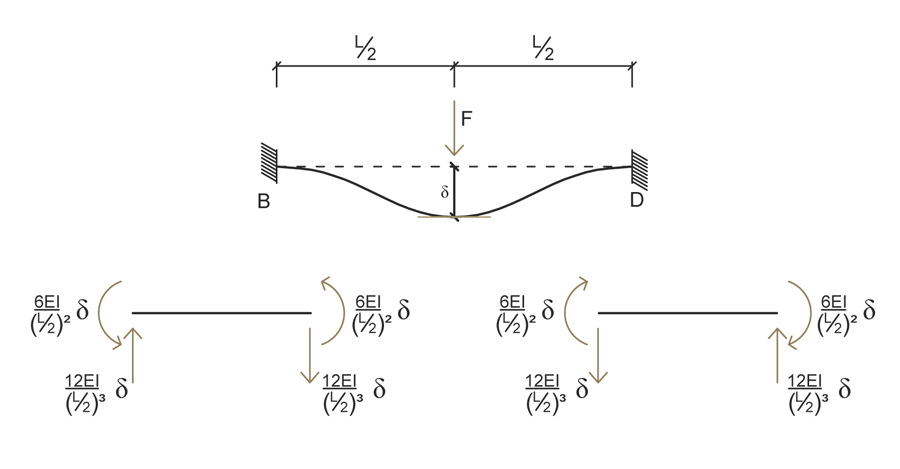
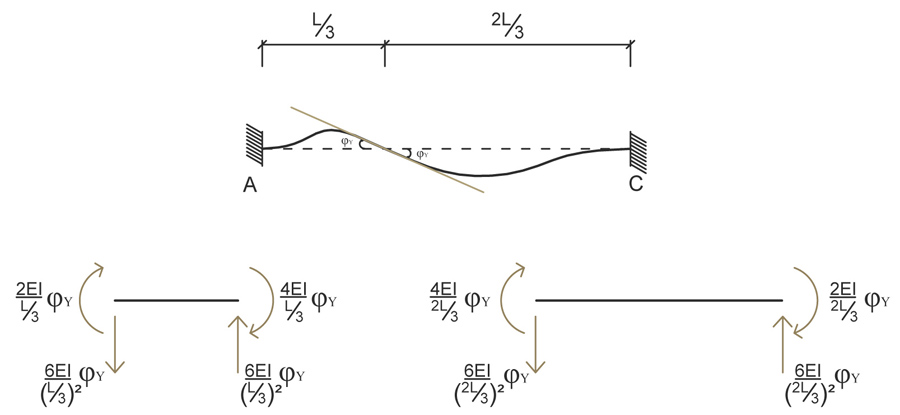
Facciamo agire solo la rotazione
Sempre grazie agli schemi notevoli di una trave doppiamente incastrata con una rotazione applicata ad un estremo, possiamo ricavarci valori del taglio e momento
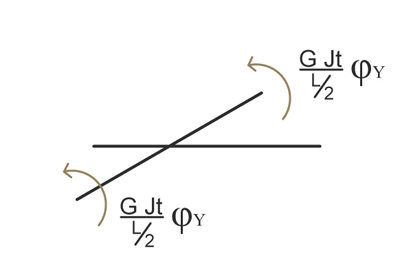
La flessione della trave AC intorno all’asse y corrisponde inevitabilmente alla torsione di quella BD:
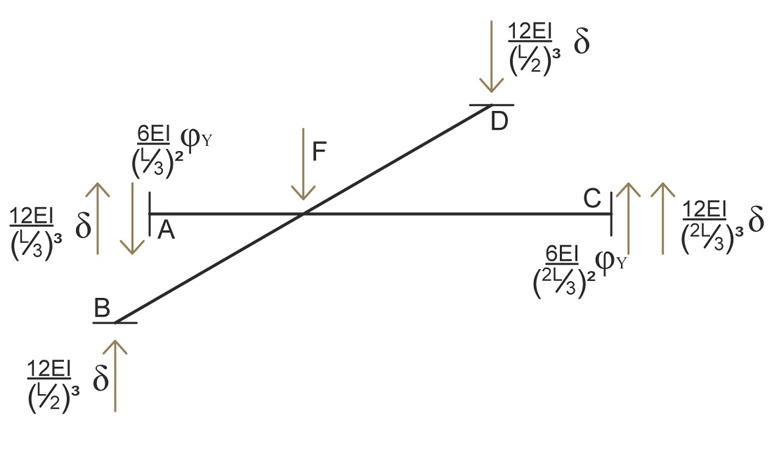
Applicando la sovrapposizione degli effetti al nodo centrale, otteniamo le seguenti forze
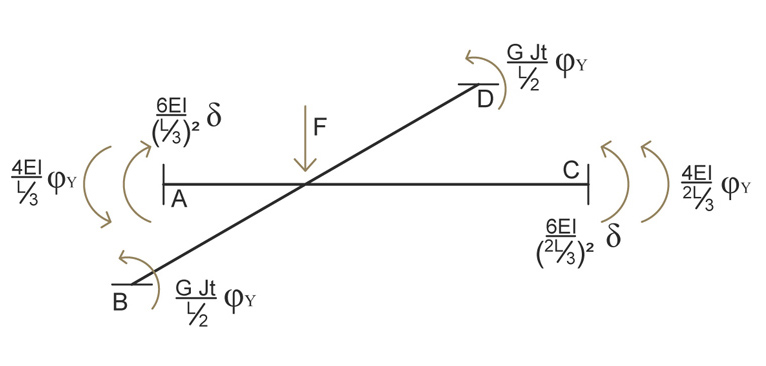
Mettendo a sistema le due equazioni
VERIFICA IN SAP
Verifichiamo con SAP la sezione in calcestruzzo calcolata a mano, e come nell'esercizio della rigidezza torsionale fatto in precedenza, con le altre sezioni scelte, cioè:
. Sezione RETTANGOLARE in CALCESTRUZZO ARMATO
· Sezione CIRCOLARE PIENA in CALCESTRUZZO ARMATO
· Sezione DOPPIA T in ACCIAIO
· Sezione QUADRATA CAVA in ACCIAIO
· Sezione TUBOLARE in ACCIAIO
DEFORMATA DIAGRAMMA MOMENTO
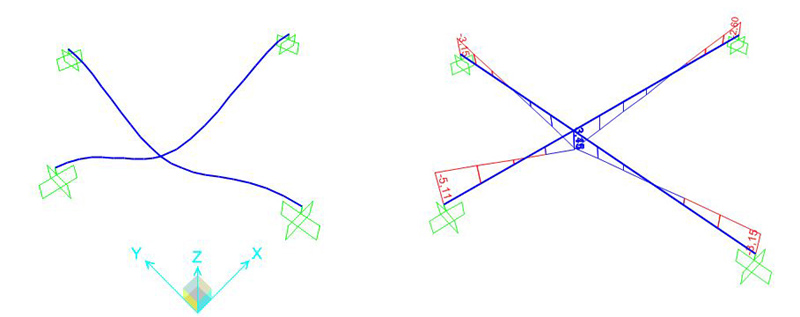
DIAGRAMMA TAGLIO DIAGRAMMA TORSIONE
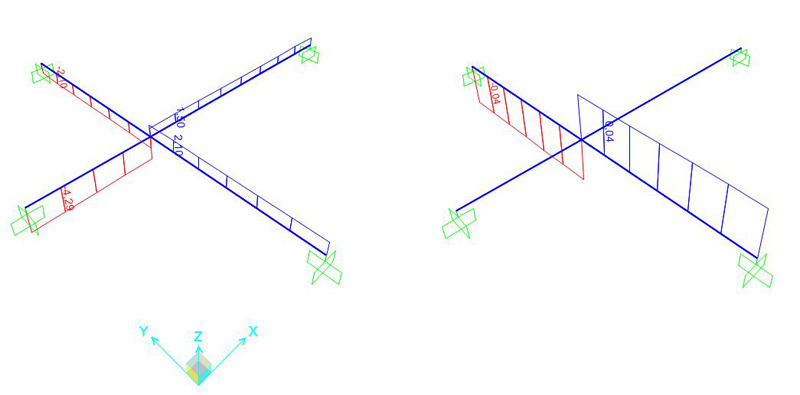
I risultati ottenuti sono stati riassunti in una tabella

