Facoltà di Architettura - Università degli Studi Roma Tre
Es2_Dimensionamento elementi Solaio.
Per questa esercitazione ho deciso di utilizzare un solaio ad interasse variabile; gli interassi e luci della struttura sono ampi per permettere di studiare come, oltre un certo fattore, non convenga utilizzare una determinata tecnologia.
Il primo caso studio è quello di un SOLAIO IN LEGNO LAMELLARE GL32c.
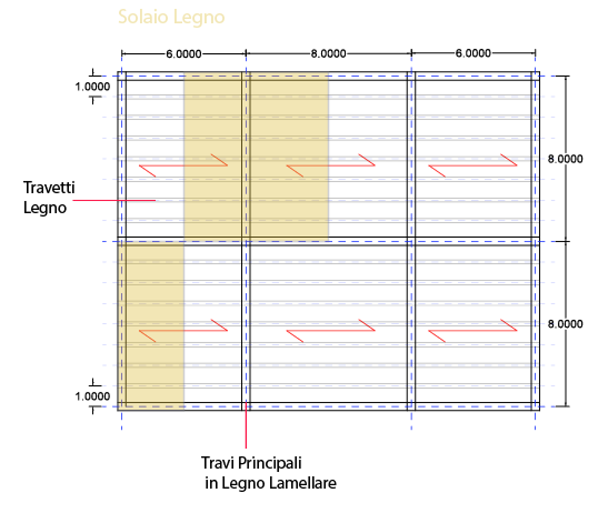
Esso, come visibile nell’ immagine, risulta caratterizzato da un sistema composto da 4travi principali e i relativi travetti [7, posizionati ad interasse standard di 1 metro].
L’interasse delle Travi è variabile, ma noi prenderemo l’area di influenza maggiore su una singola trave, equivalente a 7m di larghezza per 8 di lunghezza. [Inseriremo dunque 7 nella colonna “Interasse” di Excel, e 8 nella colonna “Luce” di excel.]
Guardando la sezione, possiamo vedere come esso sia composto da una stratigrafia così composta:
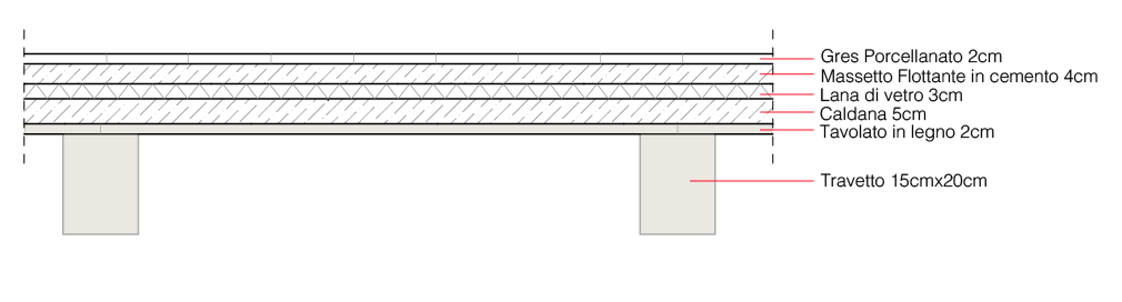
Travetto 15cmx20cm
Tavolato in legno 2cm
Caldana 5cm
Lana di vetro 3cm
Massetto Flottante in cemento 4cm
Gres Porcellanato 2cm
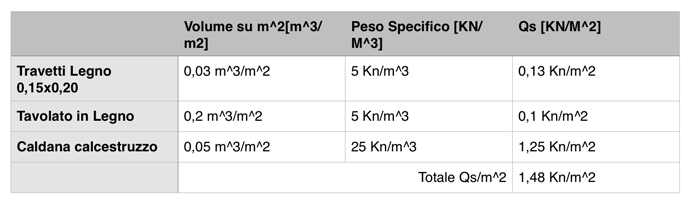
Iniziamo dunque a definire i Carichi Strutturali, Permanenti e Quelli Accidentali.
Per carichi strutturali intendiamo i carichi della struttura, senza i quali elementi la struttura sarebbe impensabile [Travetti in legno, tavolato in legno, caldana].
Si noti come in prima istanza il PESO PROPRIO DELLA TRAVE NON VENGA CONSIDERATO.
Carichi permanenti sono quei carichi che saranno sempre presenti nella struttura, ma non sono determinanti per il suo equilibrio strutturale [ isolante, massetto flottante e grès porcellanato].
Carichi Accidentali sono i carichi dipendenti dalla funzione della struttura [abitazione, ufficio al pubblico, ufficio chiuso al pubblico, etc..].
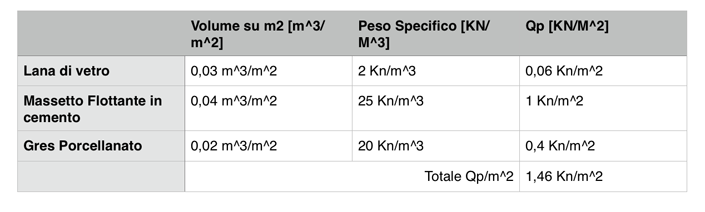
Per tutte e tre le ipotesi di studio dei solai [legno, acciaio e c.a] verrà previsto una Funzione Ad uso ufficio di categoria B1, con Carico Accidentale Qa di 2 Kn/m^2.
Si procederà dunque all’ inserimento dei dati relativi a Qstruttuali, Qpermanenti e Qaccidentali nella tabella excell.
Verrà ora visualizzato il Momento massimo alla quale la trave è sottoposta.
Procederemo poi all’inserimento della classe di resistenza a flessione del legno, caratteristica per ogni legno. Ho scelto il Legno Lamellare GL32c, il quale ha resistenza di 32 N/mm^2, poiché la luce del solaio è decisamente ampia [8m]. Maggiore la resistenza, Migliore sarà il comportamento a flessione della trave.
Dobbiamo poi inserire il Kmod, coefficiente che abbassa la tensione di Progetto, tenendo conto di fattori ambientali. Noi sceglieremo una “Classe di Servizio 2”, cioè caratterizzata da un’umidità del materiale in equilibrio con l’ambiente a una temperatura di 20°C e un’umidità relativa del’’aria circostante che superi l’85% solo per poche settimane l’anno.
Con Classe di Servizio 2 con Durata del Carico Media, inseriremo come coefficiente 0.8.
Come base della trave ho scelto 35 cm, già ipotizzando che essa verrà abbastanza alta.
Inseriti tutti i dati, otterremmo la dimensione minima dell’altezza della trave, la quale tuttavia ancora non considera il suo peso proprio.
Passaggio successivo sarà quindi inserire anche il suo peso aggiungendolo direttamente già nel valore dei carichi distribuiti Kn/m: aggiungeremo 1,05 Kn/m moltiplicandolo per il coefficiente dei carichi strutturali 1,3.
Controlleremo la sezione minima ora ottenuta.
Il nuovo risultato MINIMO DI ALTEZZA DELLA SEZIONE DELLA TRAVE è 61,77m.
Ritengo che una trave di altezza 0,65 possa dunque essere sufficiente.
Trave: 35x65 cm.
Travetti: 15x20cm
Come ipotizzabile, la sezione del legno risulta notevole in dimensioni.
Indaghiamo ora cosa accade in un SOLAIO D’ACCIAIO CON TRAVI IPE.
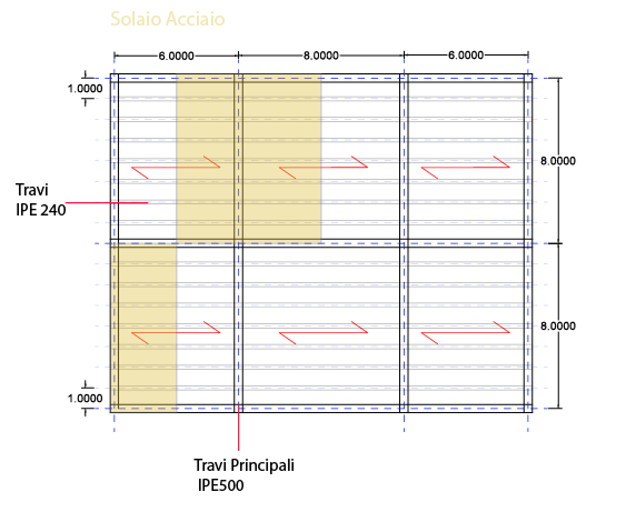
Come prima, l’interasse delle Travi è variabile, ma noi prenderemo l’area di influenza maggiore su una singola trave, equivalente a 7m di larghezza per 8 di lunghezza. [Inseriremo dunque 7 nella colonna “Interasse” di Excel, e 8 nella colonna “Luce” di excel.]
Guardando la sezione, possiamo vedere come esso sia composto da una stratigrafia così composta:
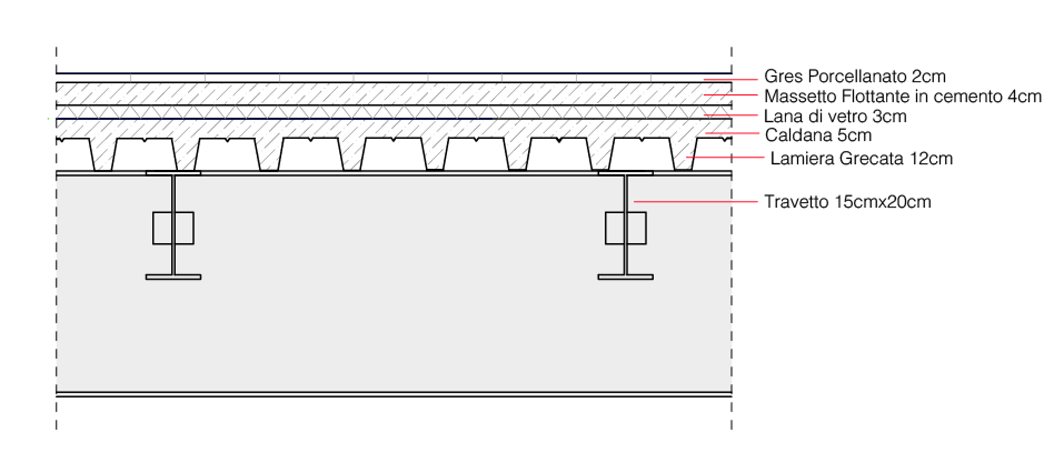
Trave acciaio ancora ignota.
Lamiera Grecata 12cm
Gettata in Calcestruzzo 5cm
Lana di vetro 3cm
Massetto Flottante in cemento 4cm
Gres Porcellanato 2cm
Per prima cosa, sarà necessario calcolare il peso al quale sono sottoposte le Travi secondarie in acciaio, così da definire quale sia effettivamente la loro giusta dimensione.
Ogni trave secondaria avrà interasse di 1 metro e luce di 6 metri. Inseriremo questi due parametri nella tabella Excel.
Successivamente, inizieremo a compilare i dati relativi a Qs e Qp e Qa ai quali le travi sono sottoposte.
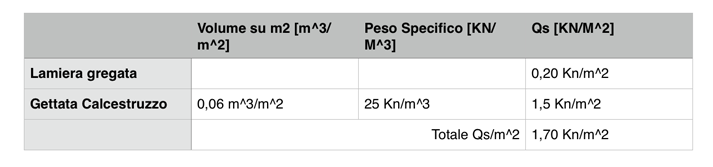
Per tutte e tre le ipotesi di studio dei solai [legno, acciaio e c.a] verrà previsto una funzione ad uso ufficio di categoria B1, con carico accidentale Qa di 2 Kn/m2.
Si dovrà decidere la Classe di resistenza dell’acciaio [le comunemente utilizzate sono S235, 2275, S325], le quali indicano il valore massimo di snervamento dell’acciaio. Io ho scelto il S235, quello con minore resistenza allo allo snervamento.
Nella colonna I otterremo dunque la Tensione massima ammissibile, nel nostro caso 204,35.
Nella colonna J comparirà il modulo di resistenza a flessione [Wx=278,27 cm^3].
Conoscendo la resistenza massima che la nostra trave, sotto queste condizioni di carico può avere, sceglieremo dal profilario una trave con valore Wx MAGGIORE a quello ottenuto.
La trave con resistenza subito maggiore a quella minima ottenuta è la IPE 240.
Conoscendo i valori della IPE240, innanzitutto andremo ad inserire il suo peso specifico nel calcolo dei Qstrutturali, e ricontrolleremo il calcolo di tutta la trave.
Il nuovo modulo di resistenza a flessione sarà 287,3 m^3 cioè minore della Wx massima di una IPE240, di conseguenza la resistenza della trave IPE240 è verificata.
Si procederà ora al calcolo della trave principale in acciaio.
I carichi strutturali sono quelli poc’anzi definiti, poiché in questo primo calcolo NON andremo ad inserire il peso proprio della Trave principale.
Qs sarà dunque 1,88 Kn/m2.
L’interasse sarà però di 7 e la luce massima di 8 metri.
Per la classe di resistenza della trave principale ho scelto una S275, cosicché l’acciaio abbia il limite di snervamento a 275 kN.
Il modulo di resistenza a flessione Wx ottenuto è 1728,50 m^3 [decisamente alto].
Secondo questo dato, la IPE da scegliere sarà una IPE500, la quale ha Wx massima 1930 m^3.
Passaggio successivo sarà quindi inserire anche il peso della IPE500, aggiungendolo direttamente già nel valore dei carichi distribuiti Kn/m: aggiungeremo 0,91 Kn/m moltiplicandolo per il coefficiente dei carichi strutturali 1,3.
Controlleremo la sezione minima ora ottenuta.
La resistenza a flessione ora trovata è 1768,07 M^3. Questo valore, essendo inferiore al valore di resistenza massima Wx della IPE500, di 1930 M^3, verifica dunque la situazione necessaria di Sdesign/Mmax < Wx.
Sceglieremo quindi Trave IPE500 per le travi e IPE240 per le travi secondarie.
Indaghiamo ora cosa accade con un SOLAIO IN CEMENTO ARMATO.
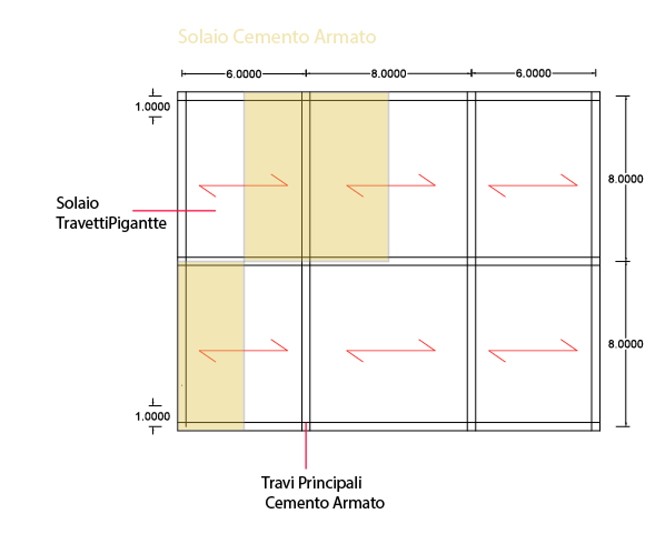
Come prima, l’interasse delle Travi è variabile, ma noi prenderemo l’area di influenza maggiore su una singola trave, equivalente a 7m di larghezza per 8 di lunghezza. [Inseriremo dunque 7 nella colonna “Interasse” di Excel, e 8 nella colonna “Luce” di excel.]
Guardando la sezione, possiamo vedere come esso sia composto da una stratigrafia così composta:
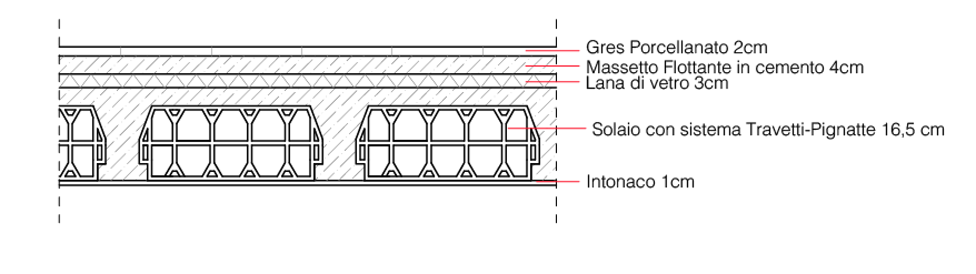
Solaio Sistema Trave-Pignatta: Pignatta 0.40*0,165 cm + Calcestruzzo armato
Lana di vetro 3cm
Massetto Flottante in cemento 4cm
Gres Porcellanato 2cm
Per prima cosa, sarà necessario calcolare il peso al quale sono sottoposte le Travi così da definire quale sia effettivamente la loro giusta dimensione.
L’ interasse maggiore è quello di di 7 metri e la luce di 6 metri. Inseriremo questi due parametri nella tabella Excel.
Successivamente, inizieremo a compilare i dati relativi a Qs e Qp e Qa ai quali le travi sono sottoposte.
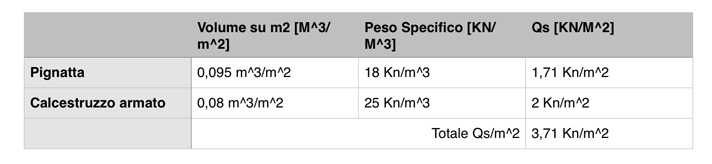
Calcoleremo poi i Qpermanenti.
Per tutte e tre le ipotesi di studio dei solai [legno, acciaio e c.a] verrà previsto una funzione ad uso ufficio di categoria B1, con carico accidentale Qa di 2 Kn/m2.
Inizieremo poi ad inserire/decidere i dati mancanti:
Classe di resistenza dell Acciaio da Armatura: 450 Mpa
Classe di Resistenza del calcestruzzo: 45 Mpa
Base trave ipotizzata: 30 cm
Delta: 5 cm
Inseriti i dati, avremo l’altezza preventivata della trave: 63,7 cm [inclusi i 5 cm di copriferro].
A questo punto sarà però opportuno verificare la trave inserendo nuovamente il suo peso proprio.
Sapendo che ogni sezione della trave preventivata è 0,19 m^2, avremo 0,19m^3 di trave su 1 m2 di solaio: il peso specifico del calcestruzzo armato è 25 Kn/m^3: il risultato Q sarà dunque 4,75 Kn/m.
Inseriremo poi il peso moltiplicandolo per il coefficiente dei carichi Strutturali Qs 1,3.
La nuova altezza della trave è 67 cm, quindi sceglieremo una trave 30x70cm.
Facendo un confronto, si otterrà la seguente situazione. Come prevedibile, l’acciaio risulta essere il materiale che meglio si addice ad un solaio a travi semplici con luci di 8 metri.
Interessante notare come il Legno e la trave di cemento armato abbiano pressoché la stessa dimensione.
