blog di lorenzo-tosti

Ho avuto problemi nell'uplodare le immagini, ma non capisco il perchè.

Allego duqnue il file pdf con l'esercitazione. :)

Questa esercitazione è incentrata sullo studio delle rigidezze di un impalcato ad un piano. 

Innanzitutto, definiamo la pianta dell’ impalcato, in Cemento Armato. Il calcestruzzo prescelto è di classe di resistenza C25/30. 

Passaggio successivo sarà la schematizzazione dell impalcato con le “Molle” Kon Kvn, le quali indicano la rigidezza di un telaio, il quale per sua conformazione è considerabile un controvento. 

Definiamo subito come la sezione dei pilastri scelti sia 0,4 x 0,4, per meglio studiare il comportamento della struttura. In fase successiva, dopo una prima analisi, verrà chiarito quale direzione della sezione dovrà essere maggiorata per contrastare la rotazione e/o traslazione del telaio.

L’altezza dell’impalcato totale è data a 4,2 m di cui 0,70 m di travi e 3,50 m di pilastro. Le travi, con sezione di 0,3 x 0,7, mirano a sintetizzare il modello di telaio Shear Type: questo modello è caratterizzato dall’avere Trave e pilastri con una grande differenza di Modulo di Inerzia, assumendo inoltre che la trave sia infinitamente rigida a flessione. 

 

Iniziamo ad inserire i dati.
Modulo inerzia del pilastro: b*h^3/12= 0,4 x 0,4 x 0,4 x 0,4 /12 =  213333 cm^4
Modulo elasticità CA: nonostante la normativa suggerisce di utilizzare il semplice modulo di elasticità del Calcestruzzo, che è 31475,81 N/mm^2, utilizzeremo il valore di SAP così da poter controllare i risultati in maniera più accurata. Adotteremo E= 24855,57 N/mm^2.

Utilizziamo questi dati per tutti i telai della nostra struttura.

Calcoliamo poi le distanze dei telai rispetto all’origine 0.
Inseriamo poi la distanza rispetto al punto O di origine degli assi. 

Troveremo cosi le distanze dei controventi dal centro delle rigidezze, e la relativa rigidezza torsionale totale. 

Nello Step5 inseriremo dunque i carichi permanenti di natura strutturali - 2,50 Kn/mq- i carichi permanenti-  3,0 Kn/Mq- e i carichi accidentali- 3,0 kn/mq.

A questo punto avremmo ottenuto tutti le forze a cui ogni controvento/telaio sarà soggetto. 

Il passo successivo è la modellazione in SAP del telaio precedentemente studiato. 

Definiamo i vincoli a terra.

Definiamo le sezioni delle travature.

 

 

Definiamo le sezioni dei pilastri.

 

Definiamo il centro delle rigidezze, utilizzando i dati ottenuti dalla tabella excell. Il centro si trova a coordinata X 6,51  e coordinata Y 4,91.

Definiamo l’impalcato rigido del “solaio”: selezionando tutti i Joints dell’impalcato Assign> Joints> Constrain. A questo punto dal menu a tendina selezioniamo DIAPHRAM, che conferisce all’intera aria selezionata rigidezza tale da non avere dilatazioni né accorciamenti, ma solo traslazioni. 

Ultimo passaggio di definizione dell’impalcatura è la caratteristica dello Shear Type: Travi infinitamente rigide a flessione. per fare ciò, selezioniamo le travi > Define>property material ed inseriamo un elevato numero di ZERI nello spazio ”momento di inerzia 2 e 3”. Così facendo il modello sarà affine a quello teorico dello Shear Type. 

A questo punto nel centro di rigidezza della struttura faremo agire la foza sismica orizzontale, precedentemente ricavata dalla tabella excell e con un valore di 126,40 Kn.

L’analisi avviata darà i seguenti risultati. 

Come visibile e prevedibile, il centro delle rigidezze non avrà nessun spostamento. 

 

 

 

In allegato il file. 

Per questa esercitazione ho deciso di utilizzare un solaio ad interasse variabile; gli interassi e luci della struttura sono ampi per permettere di studiare come, oltre un certo fattore, non convenga utilizzare una determinata tecnologia.

Il primo caso studio è quello di un SOLAIO IN LEGNO LAMELLARE GL32c.

Esso, come visibile nell’ immagine, risulta caratterizzato da un sistema composto da 4travi principali  e i relativi travetti [7, posizionati ad interasse standard di 1 metro].

L’interasse delle Travi è variabile, ma noi prenderemo l’area di influenza maggiore su una singola trave, equivalente a 7m di larghezza per 8 di lunghezza. [Inseriremo dunque 7 nella colonna “Interasse” di Excel, e 8 nella colonna “Luce” di excel.]

Guardando la sezione, possiamo vedere come esso sia composto da una stratigrafia così composta:

Travetto                   15cmx20cm 

Tavolato in legno    2cm

Caldana                   5cm

Lana di vetro           3cm

Massetto Flottante in cemento 4cm

Gres Porcellanato  2cm

 

Iniziamo dunque a definire i Carichi Strutturali, Permanenti e Quelli Accidentali. 

Per carichi strutturali intendiamo i carichi della struttura, senza i quali elementi la struttura sarebbe impensabile [Travetti in legno, tavolato in legno, caldana].

Si noti come in prima istanza il PESO PROPRIO DELLA TRAVE NON VENGA CONSIDERATO. 

Carichi permanenti sono quei carichi che saranno sempre presenti nella struttura, ma non sono determinanti per il suo equilibrio strutturale [ isolante, massetto flottante e grès porcellanato].

Carichi Accidentali sono i carichi dipendenti dalla funzione della struttura [abitazione, ufficio al pubblico, ufficio chiuso al pubblico, etc..].

Per tutte e tre le ipotesi di studio dei solai [legno, acciaio e c.a] verrà previsto una Funzione Ad uso ufficio di categoria B1, con Carico Accidentale Qa di 2 Kn/m^2. 

 

Si procederà dunque all’ inserimento dei dati relativi a Qstruttuali, Qpermanenti e Qaccidentali nella tabella excell.  

 

Verrà ora visualizzato il Momento massimo alla quale la trave è sottoposta.

 

Procederemo poi all’inserimento della classe di resistenza a flessione del legno, caratteristica per ogni legno.  Ho scelto il Legno Lamellare GL32c, il quale ha resistenza di 32 N/mm^2, poiché la luce del solaio è decisamente ampia [8m]. Maggiore la resistenza, Migliore sarà il comportamento a flessione della trave. 

 

Dobbiamo poi inserire il Kmod, coefficiente che abbassa la tensione di Progetto, tenendo conto di fattori ambientali. Noi sceglieremo una “Classe di Servizio 2”, cioè caratterizzata da un’umidità del materiale in equilibrio con l’ambiente a una temperatura di 20°C e un’umidità relativa del’’aria circostante che superi l’85% solo per poche settimane l’anno. 

Con Classe di Servizio 2 con Durata del Carico Media, inseriremo come coefficiente 0.8.

Come base della trave ho scelto 35 cm, già ipotizzando che essa verrà abbastanza alta.

 

Inseriti tutti i dati, otterremmo la dimensione minima dell’altezza della trave, la quale tuttavia ancora non considera il suo peso proprio. 

 

 

Passaggio successivo sarà quindi inserire anche il suo peso aggiungendolo direttamente già nel valore dei carichi distribuiti Kn/m: aggiungeremo 1,05 Kn/m moltiplicandolo per il coefficiente dei carichi strutturali 1,3.

Controlleremo la sezione minima ora ottenuta.

 

 

Il nuovo risultato MINIMO DI ALTEZZA DELLA SEZIONE DELLA TRAVE è 61,77m. 

 

Ritengo che una trave di altezza 0,65 possa dunque essere sufficiente. 

Trave: 35x65 cm.

Travetti: 15x20cm 

 

Come ipotizzabile, la sezione del legno risulta notevole in dimensioni.

 

 

Indaghiamo ora cosa accade in un SOLAIO D’ACCIAIO CON TRAVI IPE.

 

Come prima, l’interasse delle Travi è variabile, ma noi prenderemo l’area di influenza maggiore su una singola trave, equivalente a 7m di larghezza per 8 di lunghezza. [Inseriremo dunque 7 nella colonna “Interasse” di Excel, e 8 nella colonna “Luce” di excel.]

 

Guardando la sezione, possiamo vedere come esso sia composto da una stratigrafia così composta:

Trave acciaio ancora ignota. 

Lamiera Grecata 12cm

Gettata in Calcestruzzo 5cm

Lana di vetro 3cm

Massetto Flottante in cemento 4cm

Gres Porcellanato 2cm

 

Per prima cosa, sarà necessario calcolare il peso al quale sono sottoposte le Travi secondarie in acciaio, così da definire quale sia effettivamente la loro giusta dimensione. 

Ogni trave secondaria avrà interasse di 1 metro e luce di 6 metri. Inseriremo questi due parametri nella tabella Excel.

Successivamente, inizieremo a compilare i dati relativi a Qs e Qp e Qa ai quali le travi sono sottoposte.

 

Per tutte e tre le ipotesi di studio dei solai [legno, acciaio e c.a] verrà previsto una funzione ad uso ufficio di categoria B1, con carico accidentale Qa di 2 Kn/m2.

 

Si dovrà decidere la Classe di resistenza dell’acciaio [le comunemente utilizzate sono S235, 2275, S325], le quali indicano il valore massimo di snervamento dell’acciaio. Io ho scelto il S235, quello con minore resistenza allo allo snervamento. 

Nella colonna I otterremo dunque la Tensione massima ammissibile, nel nostro caso 204,35.

Nella colonna J comparirà il modulo di resistenza a flessione [Wx=278,27 cm^3]. 

Conoscendo la resistenza massima che la nostra trave, sotto queste condizioni di carico può avere, sceglieremo dal profilario una trave con valore Wx MAGGIORE a quello ottenuto. 

 

La trave con resistenza subito maggiore a quella minima ottenuta è la IPE 240.

Conoscendo i valori della IPE240, innanzitutto andremo ad inserire il suo peso specifico nel calcolo dei Qstrutturali, e ricontrolleremo il calcolo di tutta la trave.  

 

 

Il nuovo modulo di resistenza a flessione sarà 287,3 m^3 cioè minore della Wx massima di una IPE240, di conseguenza la resistenza della trave IPE240 è verificata. 

 

Si procederà ora al calcolo della trave principale in acciaio. 

I carichi strutturali sono quelli poc’anzi definiti, poiché in questo primo calcolo NON andremo ad inserire il peso proprio della Trave principale.

Qs sarà dunque 1,88 Kn/m2.

L’interasse sarà però di 7 e la luce massima di 8 metri.

 

Per la classe di resistenza della trave principale ho scelto una S275, cosicché l’acciaio abbia il limite di snervamento a 275 kN. 

 

Il modulo di resistenza a flessione Wx ottenuto è 1728,50 m^3 [decisamente alto].

Secondo questo dato, la IPE da scegliere sarà una IPE500, la quale ha Wx massima 1930 m^3.

 

 

Passaggio successivo sarà quindi inserire anche il peso della IPE500, aggiungendolo direttamente già nel valore dei carichi distribuiti Kn/m: aggiungeremo 0,91 Kn/m moltiplicandolo per il coefficiente dei carichi strutturali 1,3.

Controlleremo la sezione minima ora ottenuta.

 

La resistenza a flessione ora trovata è 1768,07 M^3. Questo valore, essendo inferiore al valore di resistenza massima Wx della IPE500, di 1930 M^3, verifica dunque la situazione necessaria di Sdesign/Mmax < Wx.

 

Sceglieremo quindi Trave IPE500 per le travi e IPE240 per le travi secondarie.

 

Indaghiamo ora cosa accade con un SOLAIO IN CEMENTO ARMATO.  

 

Come prima, l’interasse delle Travi è variabile, ma noi prenderemo l’area di influenza maggiore su una singola trave, equivalente a 7m di larghezza per 8 di lunghezza. [Inseriremo dunque 7 nella colonna “Interasse” di Excel, e 8 nella colonna “Luce” di excel.]

 

Guardando la sezione, possiamo vedere come esso sia composto da una stratigrafia così composta:

 

Solaio Sistema Trave-Pignatta: Pignatta 0.40*0,165 cm + Calcestruzzo armato  

Lana di vetro 3cm

Massetto Flottante in cemento 4cm

Gres Porcellanato 2cm

 

Per prima cosa, sarà necessario calcolare il peso al quale sono sottoposte le Travi così da definire quale sia effettivamente la loro giusta dimensione. 

L’ interasse maggiore è quello di di 7 metri e la luce di 6 metri. Inseriremo questi due parametri nella tabella Excel.

Successivamente, inizieremo a compilare i dati relativi a Qs e Qp e Qa ai quali le travi sono sottoposte.

 

Calcoleremo poi i Qpermanenti.

 

Per tutte e tre le ipotesi di studio dei solai [legno, acciaio e c.a] verrà previsto una funzione ad uso ufficio di categoria B1, con carico accidentale Qa di 2 Kn/m2.

 

 

Inizieremo poi ad inserire/decidere i dati mancanti: 

Classe di resistenza dell Acciaio da Armatura: 450 Mpa

Classe di Resistenza del calcestruzzo: 45 Mpa

Base trave ipotizzata: 30 cm

Delta: 5 cm

 

Inseriti i dati, avremo l’altezza preventivata della trave: 63,7 cm [inclusi i 5 cm di copriferro].

 

A questo punto sarà però opportuno verificare la trave inserendo nuovamente il suo peso proprio.

Sapendo che ogni sezione della trave preventivata è 0,19 m^2, avremo 0,19m^3 di trave su 1 m2 di solaio: il peso specifico del calcestruzzo armato è 25 Kn/m^3: il risultato Q sarà dunque 4,75 Kn/m.

Inseriremo poi il peso moltiplicandolo per il coefficiente dei carichi Strutturali Qs 1,3.

 

 

La nuova altezza della trave è 67 cm, quindi sceglieremo una trave 30x70cm. 

 

 

Facendo un confronto, si otterrà la seguente situazione. Come prevedibile, l’acciaio risulta essere il materiale che meglio si addice ad un solaio a travi semplici con luci di 8 metri.

Interessante notare come il Legno e la trave di cemento armato abbiano pressoché la stessa dimensione. 

 

 

 

 

 

 

Salve a Tutti.
Mostrero qui come ho sviluppato l'esercitazione di studio di una trave reticolare spaziale. 

Innanzitutto, ho deciso di prendere un caso di studio reale per rendere l'esercitazione più affine a ciò che normalmente si dovrebbe fare. Ho voluto studiare una trave reticolare di copertura per un progetto di un centro congressi che ho realizzato il secondo anno. 
Caratteristica principale è la grande luce da coprire nell'atrio principale, con i pochi appoggi della copertura [situati soprattutto nella zona Nord-Est dell'edificio]. Qua sotto è riportata la planimetria dell'ultimo piano con evidenziati in rosso gli appoggi della copertura.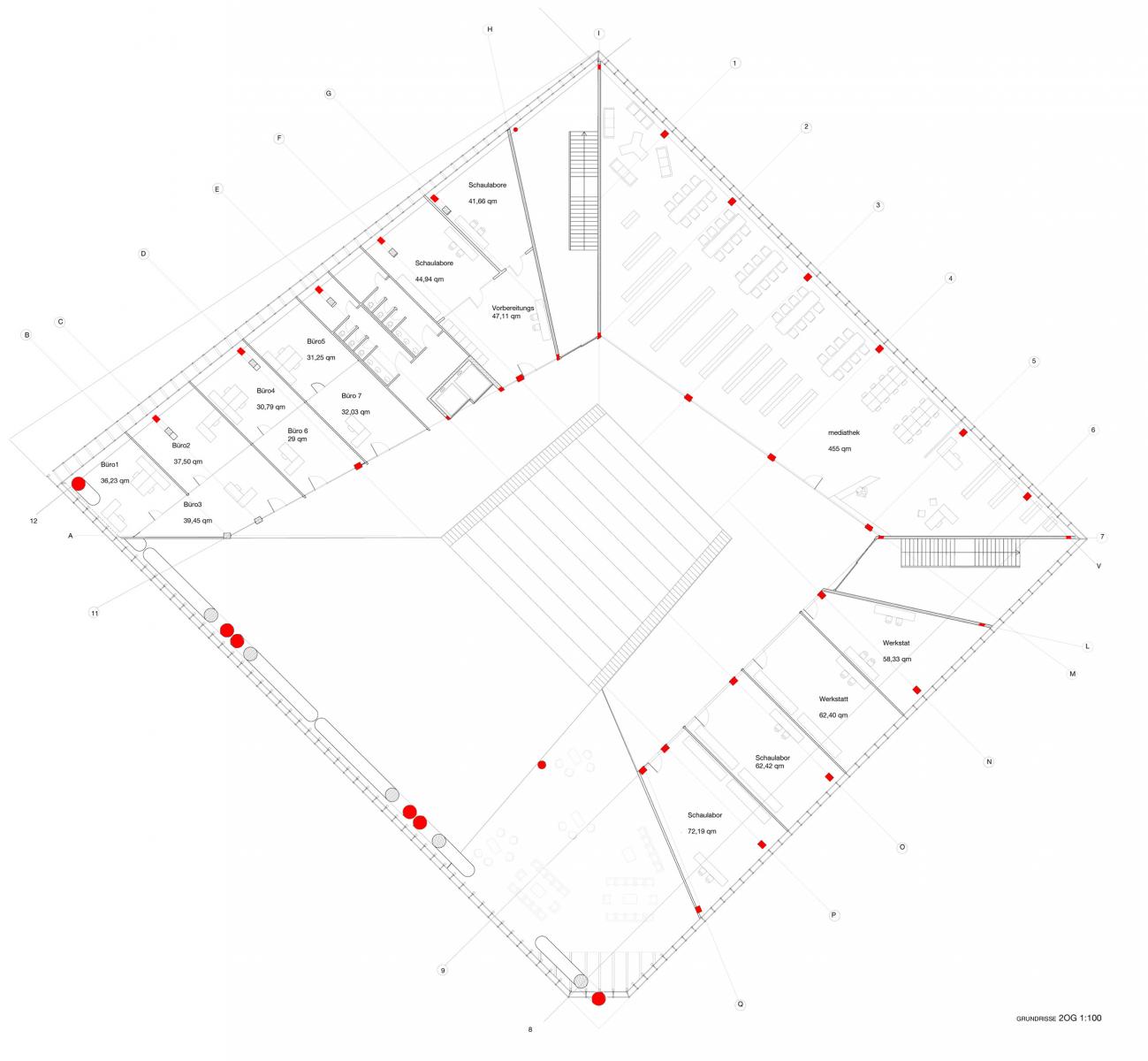 

Per la definizione della copertura ho deciso di utilizzare un modulo in pianta di 1,5x1,5- dunque abbastanza gestibile per far coincidere pilastro-cerniera- con altezza dei triangoli della copertura 2 metri.

Passaggio successivo, su Sap2000, è stata la definizione della griglia di base su cui andare a lavorare. il Risultato ottenuto è stato il seguente.  Una grigia di 42 x 35 moduli. 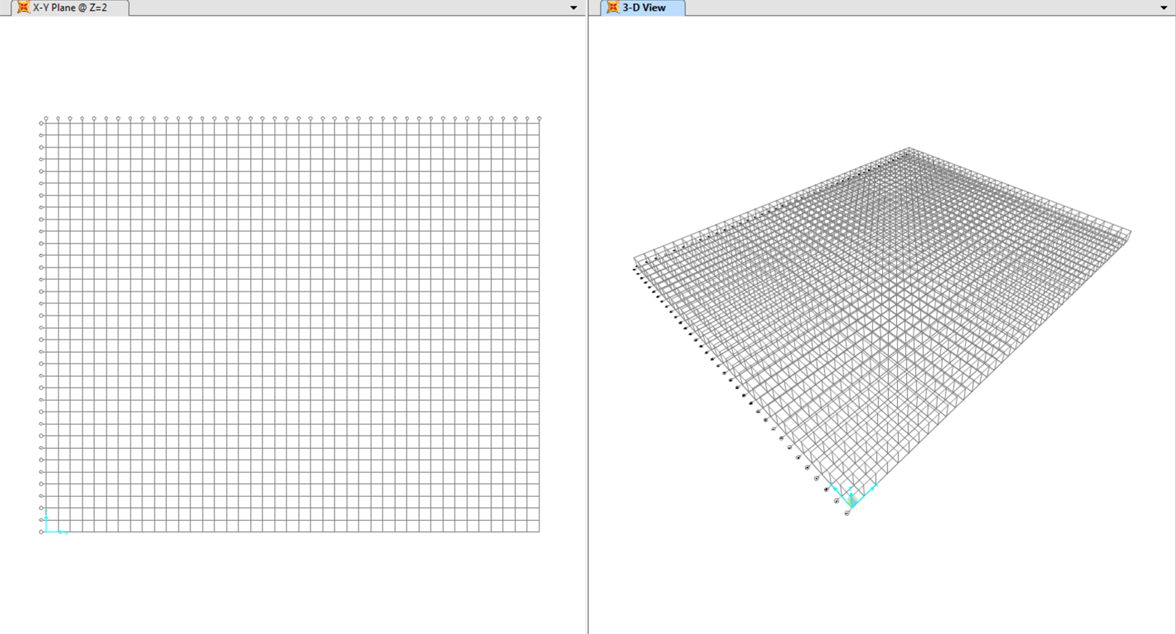 Ho poi iniziato a costruire un primo filare della trave di copertura, per poi copiarla tramite offset per tutta la griglia originaria.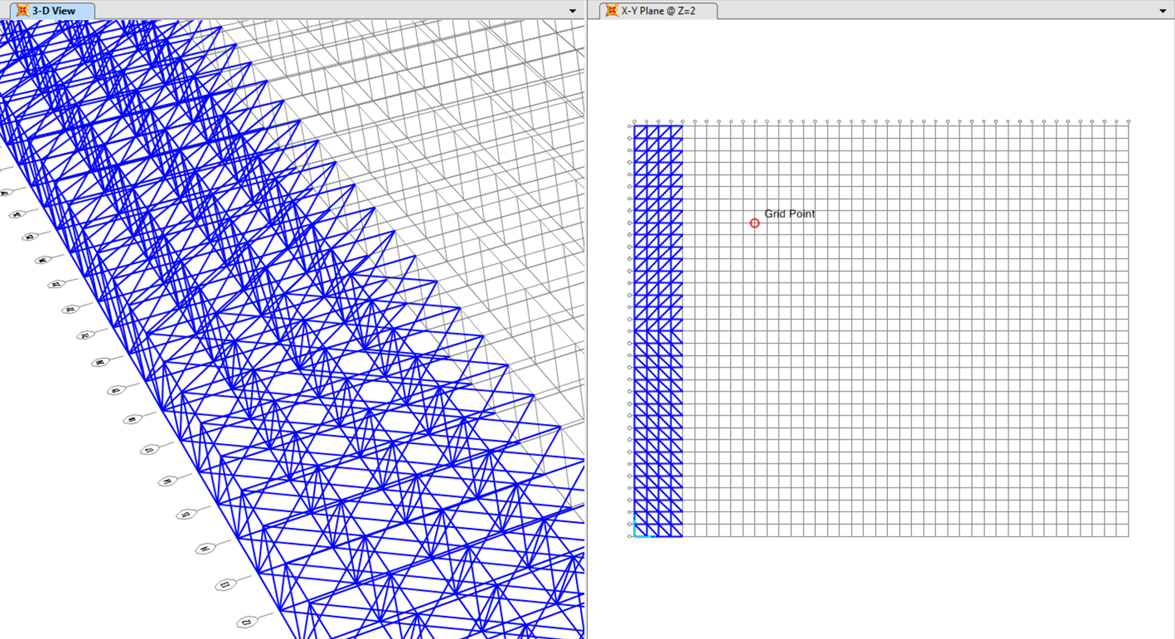 

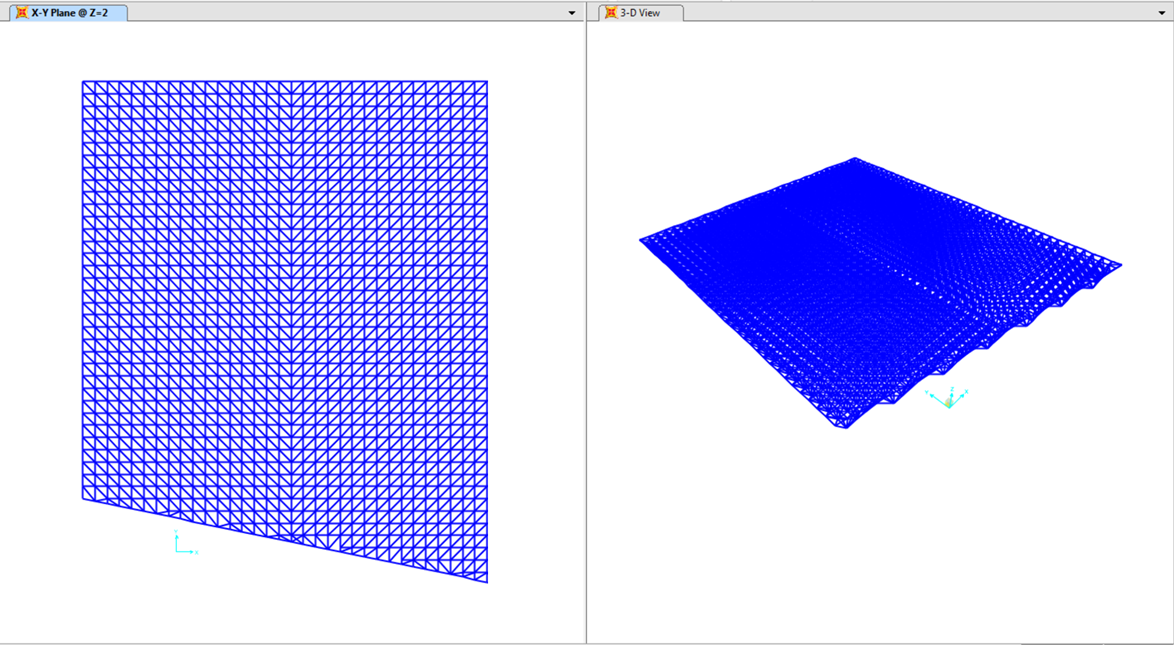
Come visibile, un lato della copertura è obliquo, ho quindi provveduto a creare delle terminazioni che seguissero il movimento obliquo della copertura, non utilizzando Frames di lunghezza maggiore a 3 metri [ragionevole lunghezza, a mio parere.]

Avendo tutti i Frames, passaggio successivo è stata la definizione delle cerniere:  selezioniamo tutti i frames del nostro modello e seguendo il percorso  

Assign>Frame>Releases/Partial Fixity

andiamo a definire che tutt i giunti delle aste sono delle Cerniere che non trasmettono il Momento [Caratteristica fondamentale in una Reticolare]. Nella finestra che si aprirà andremo a Spuntare Momento 3-3.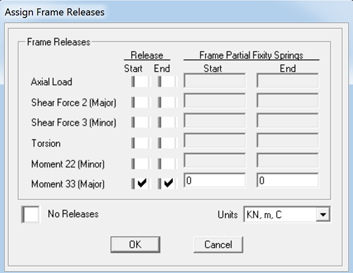

Ho cosi ottenuto questo immagine. 

Successivamente ho definito la tipologia della Sezione della copertura. Selezionando, 

Assign>Frame> Frame Section.

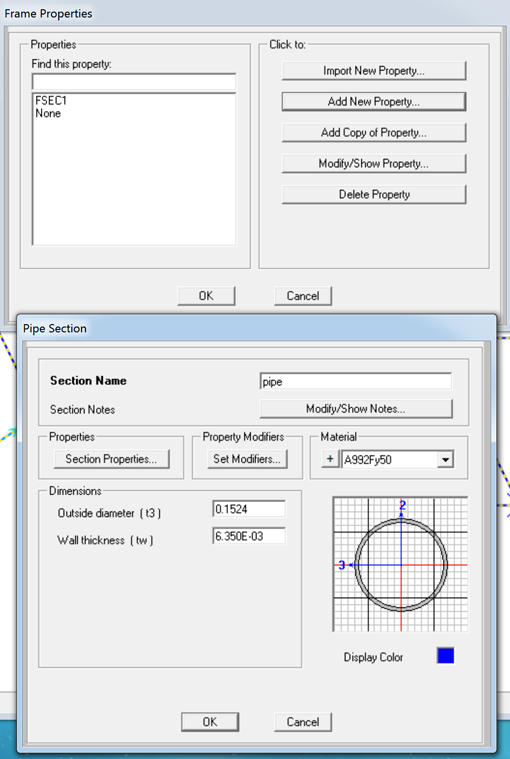
Qui ho impostato la tipologia in Acciaio con sezione Circolare da 15cm, e verrà poi mostrato sul display. 

Successivamente ho definito il terzo parametro fondamentale per lo studio della copertura e del suo funzionamento: GLI APPOGGI/CERNIERE.

Selezionando i punti necessari, 

Assign>JOINTS>JOINTS  RESTRAINTS.

Ho deciso di utilizzare solo Cerniere, che rappresentano l'appoggio sui pilastri in cemento armato.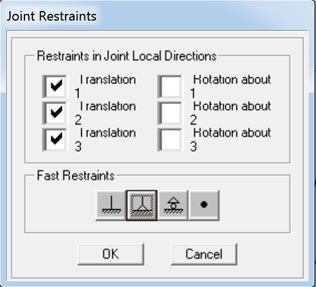 

Selezionando i JOINTS interessati, abbiamo cosi ottenuto questa schermata. In verde sono evidenziati le Cerniere. 

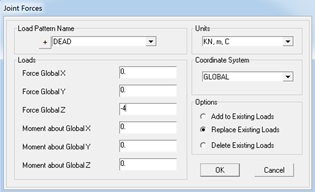
Ultimo Parametro da inserire è poi il CARICO agente sulle forze.

Selezionando TUTTI i nodi sulla parte verticale della copertura, 

Assign>joint Loads>Forces 

Ho qua impostato il Carico PUNTUALE, ipotizzando un carico per la copertura di 4KN. Inserire la forza sull'asse Z in valore negativo poichè Sap non considera la forza di Gravità. [Essendo non calpestabile e ricoperto con lastre di ALUKOBOND  non dovrebbe pesare eccessivamente].

Definite quindi le Forze, I vincoli, La tipologia di Sezione, Possiamo avviare l'Analisi Criccando su RUN nella TOOLBAR, ed evidenziando la Forza da calcolare nella seguente schermata.

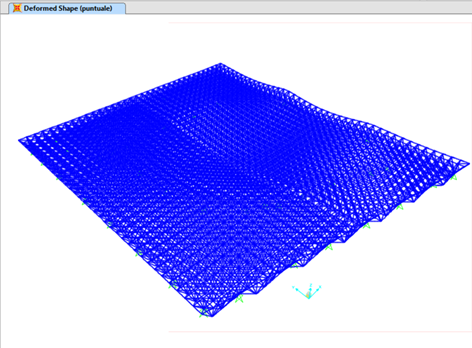
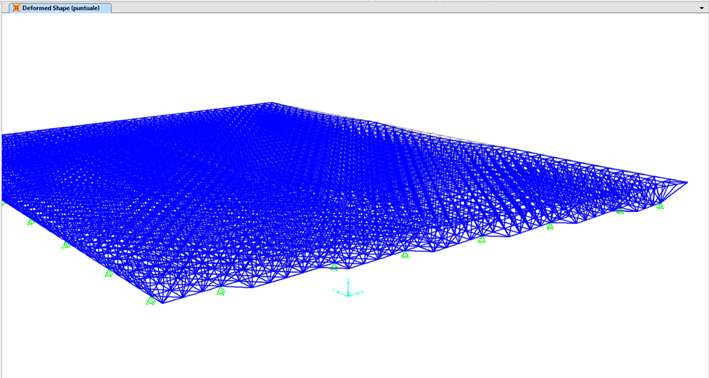
Dopo una analisi di qualche minuto, il primo risultato è la deformata.

L'immagine apparsa sullo schermo ben mostra un serio problema di deformazione della copertura.

Coprendo infatti una luce di circa 40 metri senza un appoggio, essa tende a deformarsi in maniera preoccupante utilizzando una reticolare con modulo in pianta di 1.5m x 1,5m. 

ù

IN grigio è mostrata la Indeformata. si noti inoltre come questo problema sia presente maggiormente nella zona centrale e in alto a destra, proprio le zone senza appoggi. 
Mi sorge spontaneo chiedere: Per migliorare la copertura senza intorduzione di ulteriori pilastri [cosi come era stato richiesto in fase progettuale], sarebbe migliore aumentare il modulo della reticolare, allungando i Frames, o no? Sicuramente l'altezza di 2 metri, alla luce dei dati, sembra inopportuna: forse un 3metri.

Oppure, ingrandendo la sezione FRAME SECTION, potremmo migliorare il risultato? [Magari un 20 cm di diametro anzichè 15.]

Spero di poter indagare in futuro questo aspetto, avendo migliore confidenza con il sistema di una reticolare spaziale.

Ritornando a Sap2000, ho provveduto poi all'analisi delle Forze assiali. Selezionando

Show Forces>Frames, spuntanto ASSIAL FORCES

avremo il diagramma della Forza Normale. 

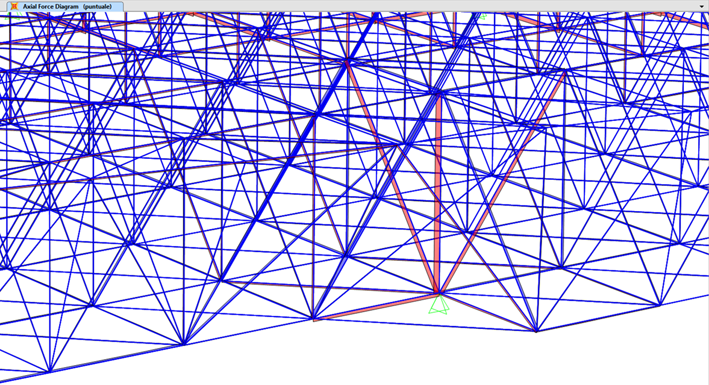
Cliccando invece su

Show Forces> Frames e spuntando MOMENT 3.3

avremo il diagramma del momento, in questa siuazione zero poichè in una rave reticolare il momento è zero [ricordiamo che precendetemente avevamo fissato come dato che la crniera non trasmettesse il momento.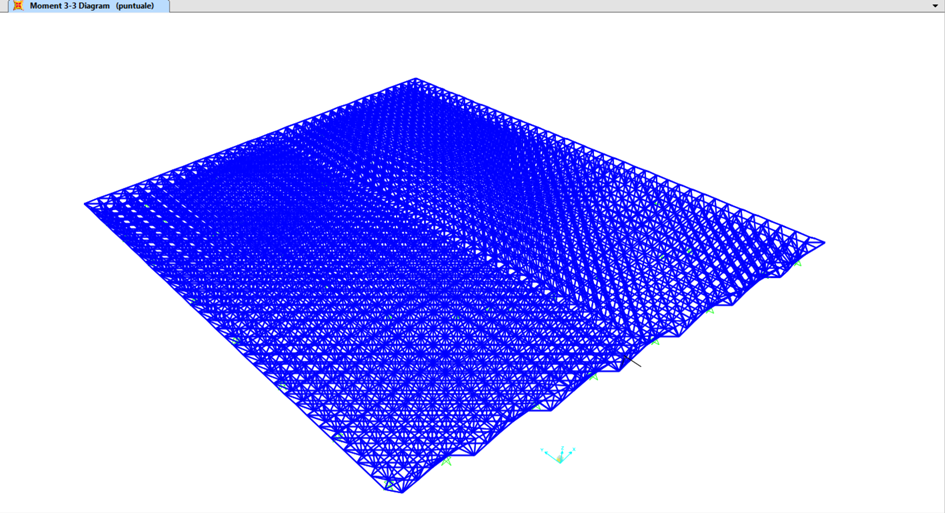

cliccando poi sull'icona nella toolbar

Show Forces>Joints

verranno mostrate le reazioni vincolari degli appoggi. 

Ritengo questo studio affrontato, come primo approccio generale, utile per intervenire nella definizione di importanti elementi quali altezza copertura- il suo sistema andrà infatti a modificare l'assetto interno dell'ambiente- e sezione dei pilastri diversamente sollecitati. 

Purtoppo Excel non riesce ad essere compatibile con Sap2000. Ma appena possibile esporterò i dati per controllare le sollecitazioni degli appoggi, dove alcuni risulteranno, per necessità, più sollecitati > un ingrandimento della loro sezione sarà allora necessario. 

Un saluto, 
Lorenzo. 

Salve a tutti.

Mostrerò ora come ho creato la trave reticolare2D sul programma Sap2000.
 

Innanzitutto sono andato a creare un nuovo File, ed utilizzando i template presenti in Sap2000 ho inserito le coordinate a mio piacere per ottenere una trave reticolare di Triangolo 3m di base per 3m d'altezza costituita da 3 triangoli.  

Fatto ciò, si presenterà sullo spazio virtuale la Trave2d con le caratteristiche da noi richieste. 

Per prima cosa selezioniamo tutti i frames del nostro modello e seguendo il percorso  

Assign>Frame>Releases/Partial Fixity

andiamo a definire che tutt i giunti delle aste sono delle Cerniere che non trasmettono il Momento [Caratteristica fondamentale in una Reticolare]. Nella finestra che si aprirà andremo a Spuntare Momento 3-3.

Questo sarà il risultato che apparirà sullo schermo.

Andiamo poi a definire la Sezione della nostra Trave [Materiale-tipologia di sezione]. Selezionando tutto,  

Assign>Frame> Frame Section.

Qui possiamo selezionare il Materiale e la sezione (quadrata, rotonda, L, e molte altre.). 
Se tutto fatto correttamente, il risultato sarà il seguente. Nel mio caso, con sezione d acciaio rotonda, ho chiamato questa tipologia PIPE. 

Definita anche la sezione, ci occuperemo della definizione dei carichi. Esseno una trave reticolare, per convenzione i carichi vengono posizionati come "Puntuali", non distribuiti. Selezionando i JOINTS interessati [nel mio caso 6, i 6 vertici dei triangoli che compongono la trave reticolare], seguire il percorso      

Assign>JOints>Forces.

Qua, cliccando sul bottone + affianco a Dead, si aprirà una schermata nella quasi si definiranno i carichi. Per carico puntuale sono andato a scrivere "Puntuale", e sotto Self Weight Multiper ho scritto ZERO [infatti non sto calcolando il peso specifico del materiale]. Cliccheremo poi su Add new Load Pattern e cliccheremo in basso su OK.

A questo punto le nostre forze compariranno sulla trave. 

A questo punto, definita la SEZIONE-TIPOLOGIA CERNIERA-FORZE AGENTI, possiamo  avviare l'analisi cliccando sul pulsante RUN nella toolbar orizzontale. 

Si aprirà una schermata, e selezioneremo il carico di cui vogliamo calcolare l'azione, poi cliccheremo RUN NOW. 

Il primo risultato è la deformata della Trave. 

cliccando poi sull'icona nella toolbar

Show Forces>Joints

verranno mostrate le reazioni vincolari degli appoggi. 

Cliccando invece su

Show Forces> Frames e spuntando MOMENT 3.3

avremo il diagramma del momento, in questa siuazione zero poichè in una rave reticolare il momento è zero [ricordiamo che precendetemente avevamo fissato come dato che la crniera non trasmettesse il momento.]

Selezionando

Show Forces>Frames, spuntanto ASSIAL FORCES

avremo il diagramma della Forza Normale. 

Avremo dunque ottenuto i risultati analitici e grafici della Deformata, Momento e Forza Normale.

[ogni singolo  Frame potrà esssere studiato cliccando con il tasto destro su di esso, e si aprirà una finestra che mostra la N, T,M].Nel nostro caso il Taglio sarà pari a zero, essendo una trave reticolare. 

I dati Potranno inoltre essere esportati come tabella in Excel cliccando su File>Export>excel File. [purtroppo nel mio caso Excel non si riesce ad aprire- appena risolverò il problema integrerà questo primo Post].

Spero di essere stato chiaro in questo primo Post, 
Lorenzo :) 

Non avevo dato tempo per caricare l'immagine , scusate! 

Ps. Stazione Av Tiburtina.

Ciao a tutti:) 

Giusto un'immagine Random della stazione AV Tiburtina.

Ciao a tutti:) 

Giusto un'immagine Random della stazione AV Tiburtina.