Facoltà di Architettura - Università degli Studi Roma Tre
Esercizio della linea elastica
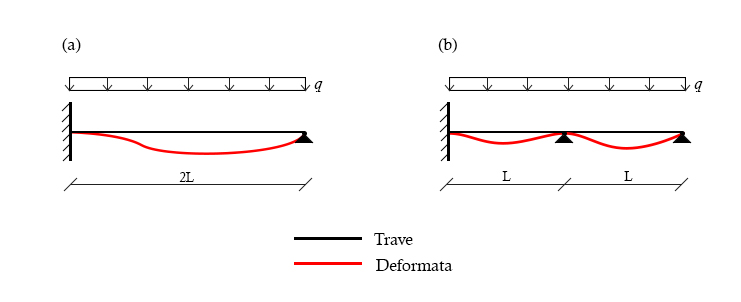FIG. 01
La FIG. 01a mostra una trave 2 volte iperstatica soggetta ad un carico q, distribuito e costante, e la sua deformata. Aggiungendo 2gdv (cioè posizionando una cerniera al centro della trave) si ottiene una trave 4 volte iperstatica. Osservando le due deformate, si può intuire come la cerniera sviluppi una reazione vincolare FBy che tende a riportare la deformata (a) verso l'alto (b).
La struttura, essendo iperstatica, non consente di calcolare immediatamente le reazioni vincolari, che si sviluppano in corrispondenza dei vincoli, con le sole equazioni di equilibrio, come si potrebbe fare in presenza di una struttura isostatica. Per arrivare a delle soluzioni quantitative sarà necessario ricorrere al metodo della linea elastica.
Per ora possiamo solo fare alcuni ragionamenti di tipo qualitativo, che saranno poi verifiati dai calcoli successivi.
La struttura è soggetta ad un carico distribuito di natura costante -> Taglio=lineare | Momento=parabolico
La deformata presenta 3 punti di flesso-> il momento si annullerà 3 volte in corrispondenza dei flessi
Vincolo di incastro -> rotazione nulla
Vincolo di cerniera -> momento nullo
Queste informazioni insieme all'analisi dei tratti in cui le fibre superiori o inferiori sono tese ci permettono di suppore ed immaginare un diagramma dei momenti e del taglio come in FIG. 02
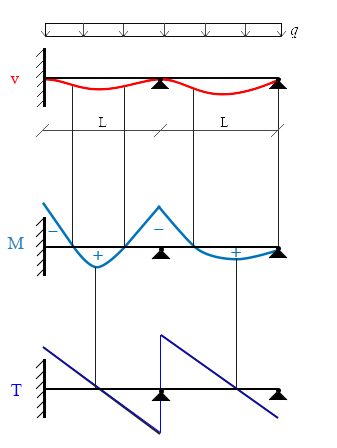FIG. 02
Per studiare la struttura iperstatica della FIG. 01b è necessario applicare 2 volte il metodo degli spostamenti, poichè la struttura presenta una singolarità. In tal modo si avrà un'equazione della linea elastica per il primo tratto lungo L (che indicheremo con i pedici 1) e un'altra equazione della linea elastica per il secondo tratto lungo sempre L (che indicheremo con i pedici 2).
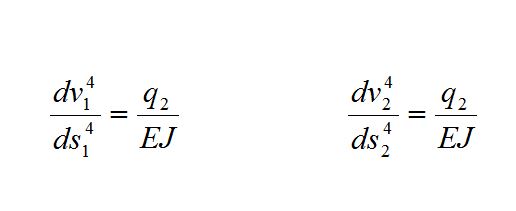
Nel caso specifico q2= -q ed il modulo di elasticità E con il momento d'inerzia J, assumono lo stesso valore, trattandosi del medesimo materiale e della stessa sezione. Si ricavano le seguenti equazioni:
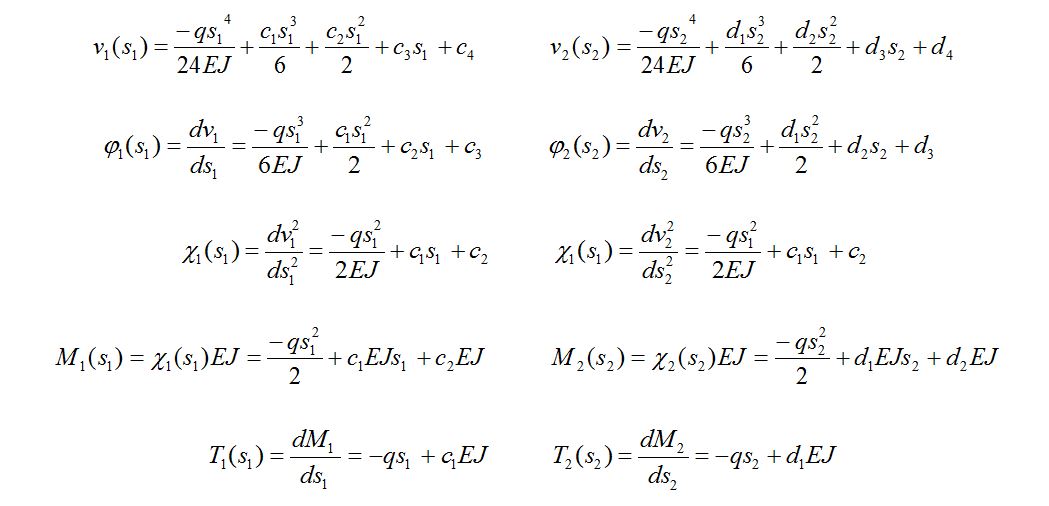
Abbiamo perciò 8 incognite, 4 per il primo tratto e altre 4 per il secondo tratto. Le prime vengono individuate con la lettera c e le seconde con la lettera d. Sarà necessario definire 8 condizioni al bordo, utili per ricavare le 8 incognite.
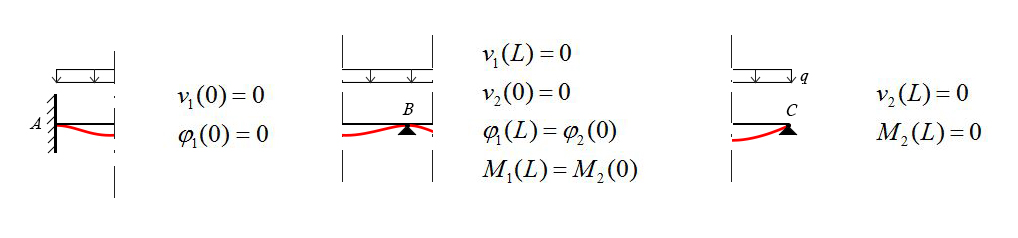
Di conseguenza il punto A fornisce 2 informazioni che corrispondono alle 2 equazioni:
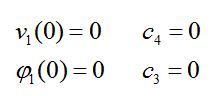
Il punto B fornisce 4 informazioni che corrispondono alle 4 equazioni:
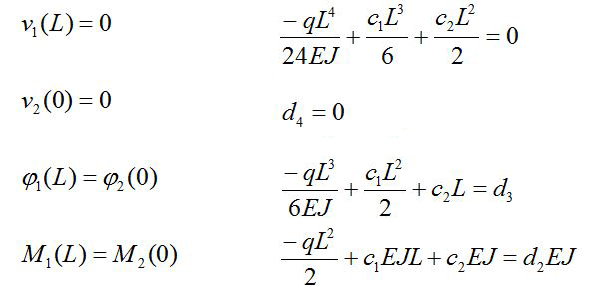
Il punto C fornisce 2 informazioni che corrispondono alle 2 equazioni:
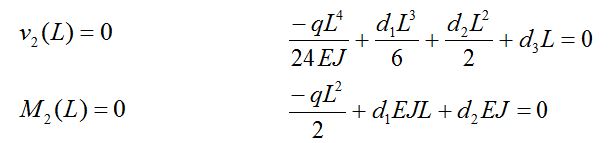
Le soluzioni che si ricavano da queste 8 equazioni sono:
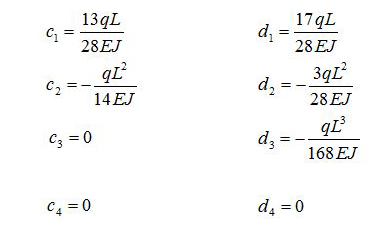
Questi risultati li sostituiremo nelle equazione iniziali ottenendo v1(s1) e v2(s2):
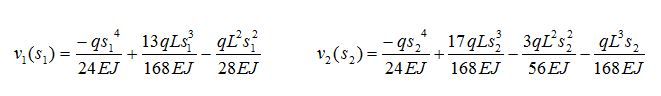
v1(s1) e v2(s2) forniscono tutte le informazioni necessarie a ricavare i diagrammi delle sollecitazioni, dai quali si possono ricavare le reazioni vincolari.
Iniziando dalle sollecitazioni di taglio, si va a calcolare il T1(s1) e T2(s2)in s=0 e in s=L, poichè in questo caso il Taglio è una funzione lineare bastano 2 valori per definirne il grafico:
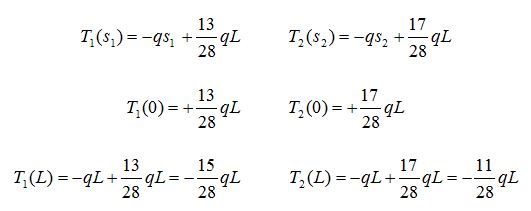
Il momento invece è descritto da una funzione di secondo grado quindi è rappresentato da una parabola che per essere disegnata ha bisogno di tre valori.
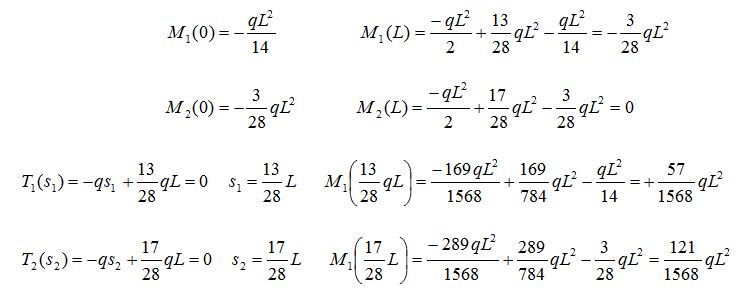
Una volta ricavati i valori possiamo disegnare i diagrammi:
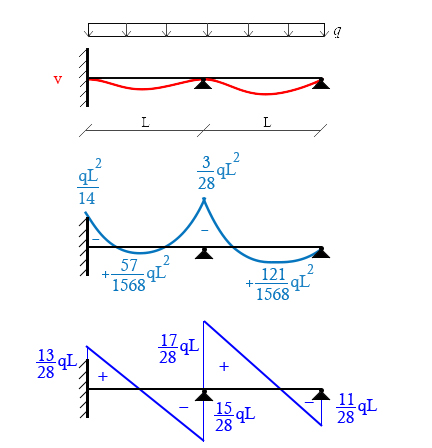
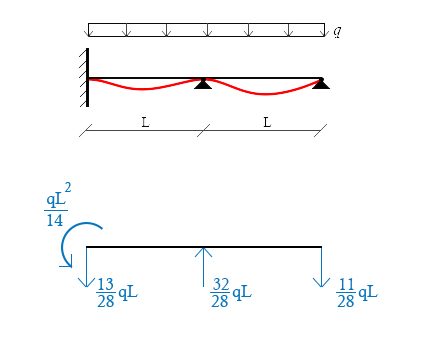
Dai diagrammi ricaviamo le reazioni vincolari:
