un foglio elettronico per la ripartizione delle forze sismiche

Impegnarsi a ripartire le forze orizzontali su di una struttura aiuta a comprendere molti concetti di meccanica strutturale.

Tra gli altri, i seguenti:

1) che la struttura, comunque sia fatta, vive nel tridimensionale;

2) che non esistono solo le azioni (carichi) verticali, ma anche azioni orizzontali, qualunque sia la loro natura (azioni sismiche, vento, spinte della terra etc.)

3) che la struttura va progettata (anzi, concepita) tenendo conto anche di queste azioni orizzontali

4) che i medesimi elementi strutturali possono avere una doppia funzione, se adeguatamente disposti nello spazio. In particolare, che un insieme di travi e pilastri, se allineati in un piano verticale,  rappresentano allo stesso tempo una struttura che sopporta i carichi verticali ma anche le azioni orizzontali (controvento)

In particolare, se ci concentriamo sulla tipologia dell'edificio e se il solaio è abbastanza rigido nel suo piano, lo sforzo di ripartire le forze sismiche equivale ad un'applicazione del metodo delle rigidezze in un sistema meccanico composto da corpi rigidi e molle elastiche.

Tuttavia, la semplicità algebrica ha un prezzo concettuale. Bisogna conoscere il concetto di rigidezza (in particolare di rigidezza traslante di un telaio shear-type) e lo spostamento rigido infinitesimo di un corpo piano (formula di Eulero). E poi aver capito bene che nella risoluzione dei sistemi elastici iperstatici le equazioni si usano tutte (equilibrio, congruenza e legame costitutivo) ed in un ordine ben preciso, definito dal metodo utilizzato (metodo delle forze, metodo delle rigidezze etc.).

Ciò premesso, ecco il problema.  Abbiamo un edificio di un solo piano definito dal seguente impalcato (pianta strutturale):

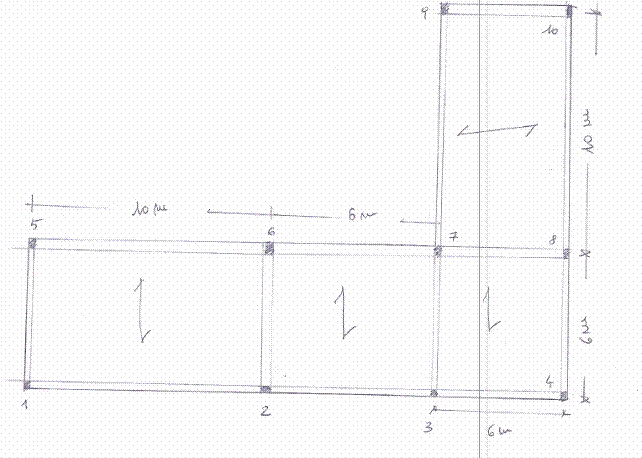
in cui i solai sono orditi come indicato in figura ed i pilastri hanno le seguenti sezioni:

Dall'analisi dell'impalcato individuiamo sette telai piani, quattro lungo Y e tre lungo X. Questi hanno il compito, oltre che di portare il peso della costruzione (struttura, sovrastruttura, sovraccarico accidentale), anche di controventare la struttura intera, ossia di resistere a forze orizzontali (nel piano X-Y), comunque orientate.

Gli elementi distinguibili che compongono la struttura sono tutti piani, ma vivono in piani diversi. Il solaio vive nel piano X-Y, 4 controventi vivono in Y-Z e tre in X-Z. Il solaio è ipotizzabile rigido nel suo piano, mentre ai controventi viene riconosciuta un'elasticità. A questo livello di semplificazione, i controventi sono vincoli (del solaio) cedevoli elasticamente e rappresentabili nel piano dell'impalcato come molle di adeguata rigidezza.

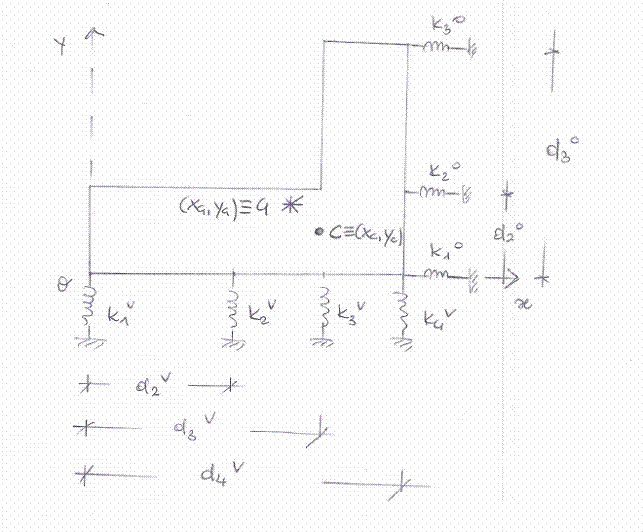
La rigidezza di ogni controvento (modellato come un telaio shear-type) viene calcolata come segue:

Ovviamente, se il controvento ha quattro pilastri al posto di due, la somma indicata in figura si estende ai momenti di inerzia dei quattro pilastri. Il coefficiente K è detto rigidezza traslante del telaio shear-type ed è funzione dei  parametri meccanici e geometrici su indicati.

Questa premessa è di base per comprendere quanto contenuto nel file excel allegato,  che ripartisce una forza orizzontale (in particolare quella sismica) sui sette controventi, attribuendone ad ognuno una frazione, che è funzione della rigidezza del controvento e della sua distanza da un punto privilegiato (il centro delle rigidezze). Molti dei concetti sopra riassunti sono contenuti in altri allegati di post precedenti a questo. Anche l'algoritmo contenuto nel file excel si riferisce a post ed allegati precedenti. 

Questo algoritmo si compone di sette passi:

Passo 1: calcolo della rigidezza del singolo controvento (in figura la tabella del controvento 1)

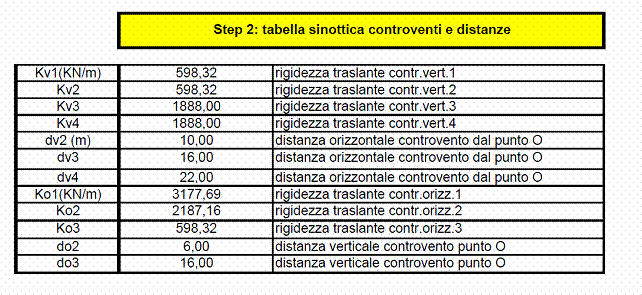
Passo 2: tabella sinottica di rigidezze e distanze dal punto O (origine degli assi) di tutti i controventi.

Passo 3: calcolo del centro di massa.

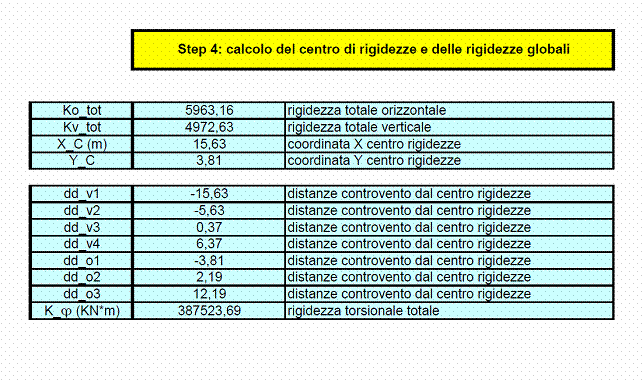
Passo 4: calcolo del centro delle rigidezze

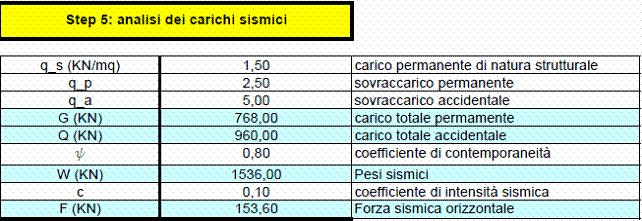
Passo 5: calcolo delle forze sismiche

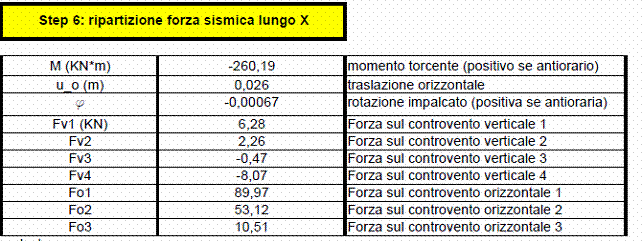
Passo 6: ripartizione forza sismica lungo X

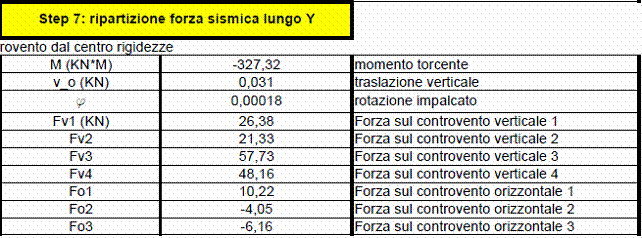
passo 7: ripartizione forza sismica lungo Y

In allegato trovate due file. L'uno contiene il file excel, l'altro il suo commento.

Il file excel è più generale di quanto si possa pensare. Anzitutto, la pianta può essere variata a piacimento, a patto che i telai rimangano diretti o lungo X o lungo Y.

Inoltre, se si effettua l'ipotesi che le sezioni dei pilastri non varino da piano a piano oppure che varino da un piano all'altro nelle medesime proporzioni, l'agoritmo di ripartizione può applicarsi anche ad un edificio multipiano, in quanto rimangono alterati sia il centro di massa sia il centro di rigidezza di ogni piano.

Ovviamente, va adeguata secondo normativa la valutazione ad ogni piano dell'azione sismica.