ESERCITAZIONE 3 - Dimensionamento di una trave a sbalzo ( C.A. , acciaio e legno)

Per dimensionare una trave a sbalzo, ovvero una mensola, bisogna individuare la trave più sollecitata come nell’esercitazione precedente.

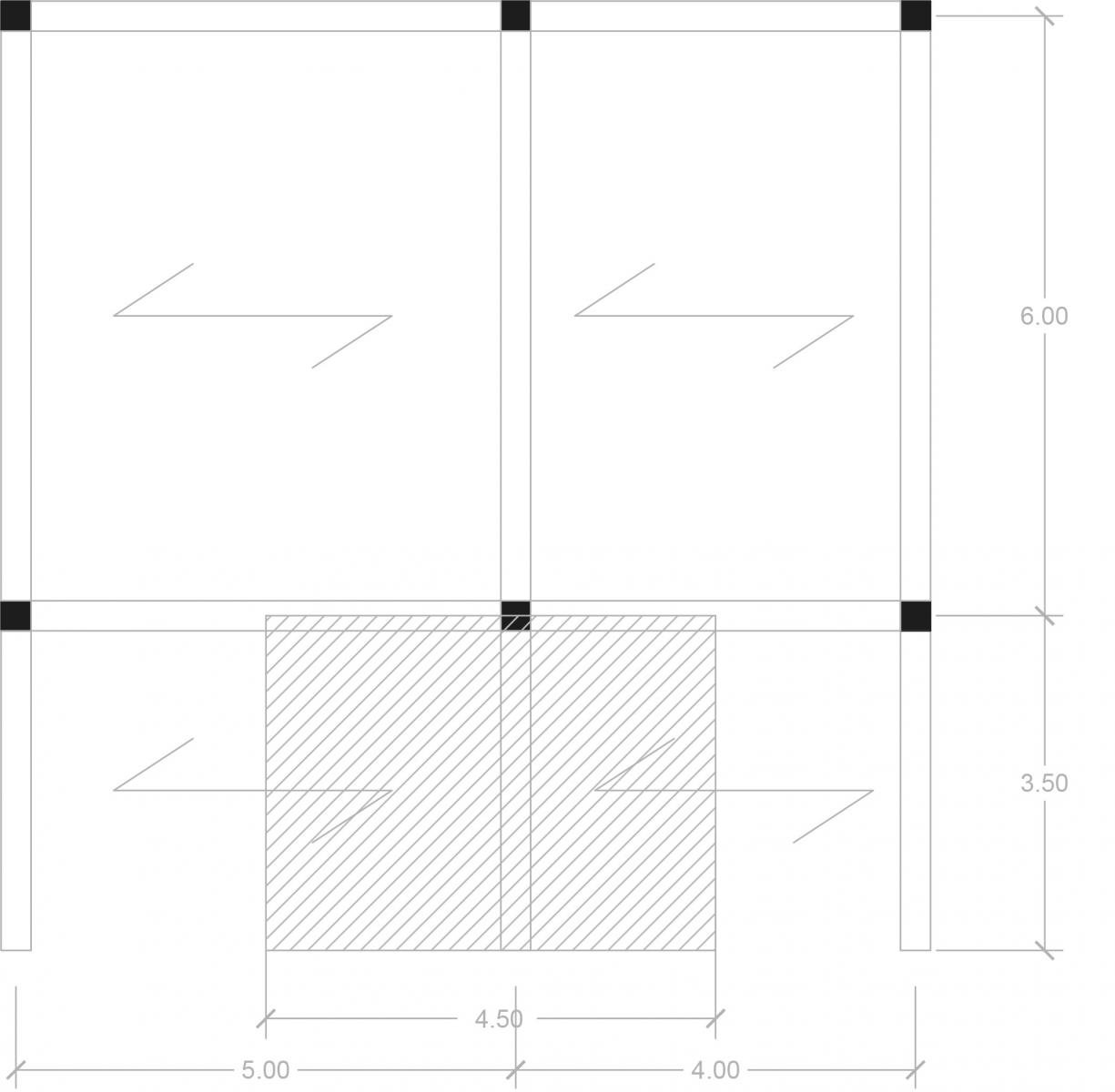
Nella prima parte bisogna sempre considerare i carichi agenti sulla trave (prenderemo come valore quelli ottenuti precedentemente).

Naturalmente cambierà il valore del momento massimo, che per una trave doppiamente appoggiata vale ql²/8, invece per una mensola il momento massimo equivale a ql²/2.

Solaio in C.A. 

Stato Limite Ultimo

Qu = 45.31 kg/m²  

M_max = 277.50 kNxm

Sezione 30x45

Stato limite di esercizio

Inserire il modulo elastico del C.A. E = 21000 N/mm²

Si ottengono i valori dell’inerzia e dello spostamento massimo, in questo caso

Ix = 227813 cm⁴

v_max = 1.18 cm

la sezione è verificata dal momento che il rapporto tra la luce e lo spostamento deve essere maggiore di 250.

Solaio in acciaio

Stato Limite Ultimo

Qu = 50.87 kg/m²  

M_max = 311.59 kNxm

IPE 450, Wx = 1500 cm³

Stato limite di esercizio

Dalla tabella prendere i valori di inerzia e peso

Ix = 33740 cm⁴

Peso = 0.77 kN/m

Di conseguenza si ricava il valore del carico di esercizio ed inserendo il valore del modulo elastico dell’acciaio si ottiene infine lo spostamento massimo.

v_max = 0.84 cm

La sezione è verificata dal momento che il rapporto tra la luce e lo spostamento deve essere maggiore di 250.

Solaio in legno 

Stato Limite Ultimo

Qu = 35.50 kg/m²  

M_max = 217.50 kNxm

Sezione 35x55

Stato limite di esercizio

Inserire il modulo elastico E = 8000 N/mm²

Si ottengono i valori dell’inerzia, del carico di esercizio e dello spostamento massimo, in questo caso

Ix = 485260 cm⁴

Qe = 20 kN/m

v_max = 0.95 cm

La sezione è verificata dal momento che il rapporto tra la luce e lo spostamento deve essere maggiore di 250.