ESERCITAZIONE 1 - DIMENSIONAMENTO TRAVE-PILASTRO CLS/ACCIAIO/LEGNO
La destinazione d’uso del progetto proposto è di tipo residenziale: l’edificio è composto da 4 piani con il medesimo schema strutturale. Per prima cosa analizziamo la pianta al fine di individuare la trave maggiormente sollecitata. La trave sottoposta ad un carico maggiore è la trave nel tratto “BC”.
Consideriamo ora la trave scelta in tre differenti tecnologie costruttive: calcestruzzo armato, acciaio e legno.
CALCESTRUZZO ARMATO
DIMENSIONAMENTO TRAVE
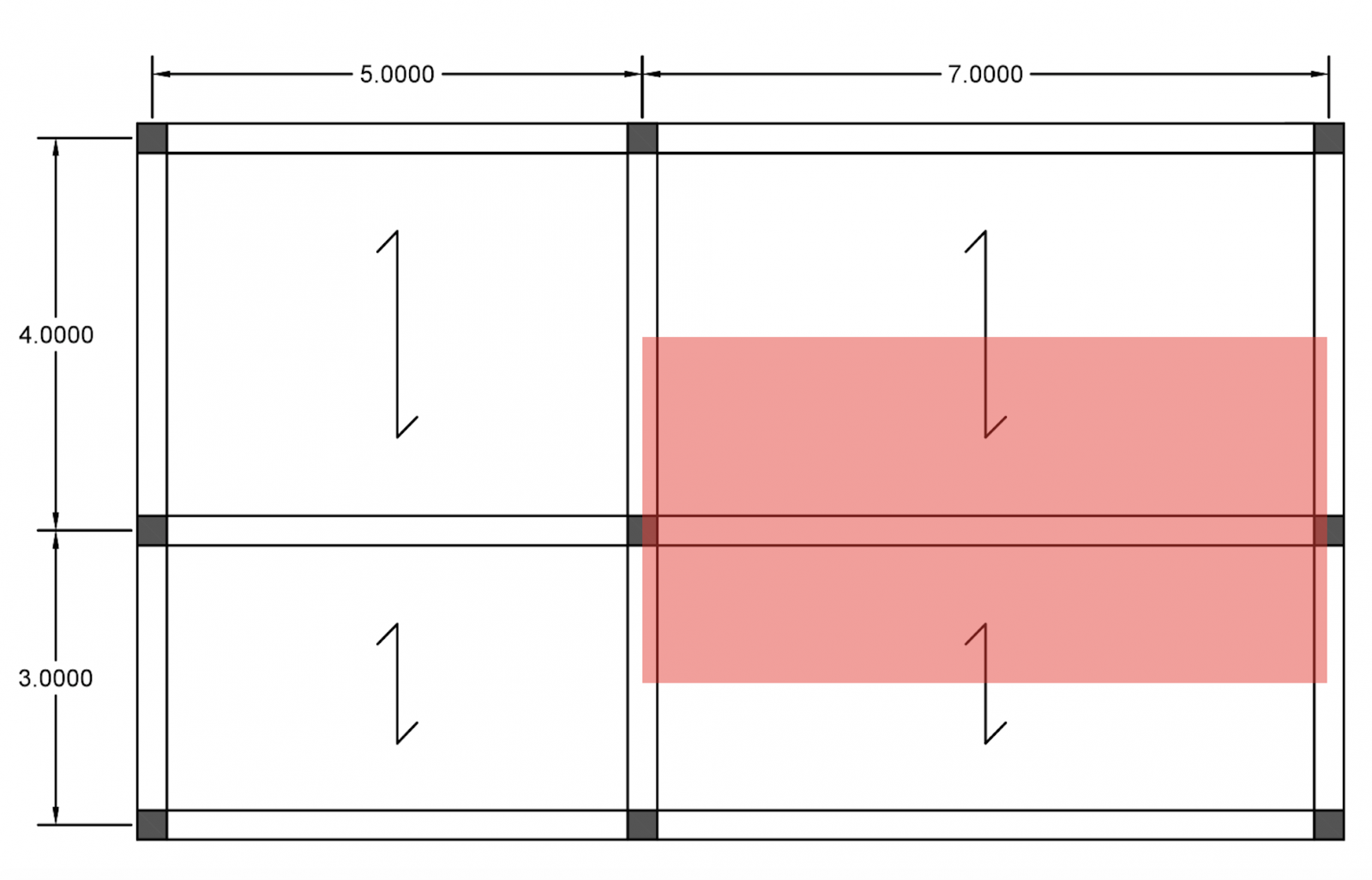
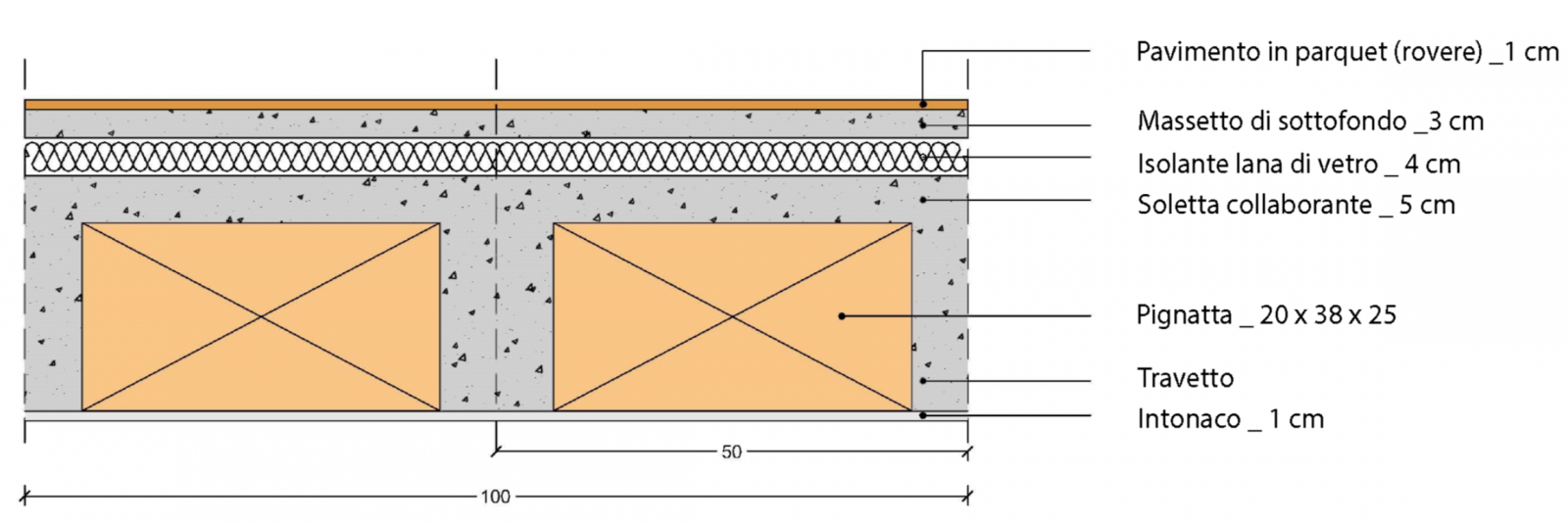
Per questo tipo di tecnologia costruttiva è stato scelto un solaio in latero cemento con travetti precompressi prefabbricati. Verrà calcolato tutto per una porzione di solaio pari a 1 m2.
Di seguito è rappresentato graficamente completo di tutte le sue parti costitutive.
ANALISI:
Il carico strutturale dipende dal peso dei travetti, della soletta in cos e delle pignatte.
TRAVETTI IN CLS:
DIMENSIONI: 12 cm x 20 cm
PESO SPECIFICO: 2500 kg/m3 = 25 kN/m3
VOLUME: 2 x 0,12 m x 0,2 m x 1 m = 0,048 m3
PESO AL METRO Q = 0,048 m3/m2 x 25 kN/m3 = 1,2 kN/m2
SOLETTA
SPESSORE: 5 cm
PESO SPECIFICO: 25 kN/m3
VOLUME: 0,05 m x 1 m x 1 m = 0,05m3
PESO AL METRO Q: 0,05 m3/m2 x 25 kN/m3 = 1,25 kN/m2
PIGNATTE
DIMENSIONI: 20 cm x 38 cm x 25 cm
PESO: 9,8 kg/cad.
PESO AL MQ: 78,4 kg/m2 = kN/m2
QS = (1,2+1,25+0,784) kN/m2 = 3,23 kN/m2
Il carico permanente Qp dipende dal peso del pavimento, del cassetto, dell’isolante e del rivestimento aggiungendo il contributo di tramezzi e impianti.
PAVIMENTO IN PARQUET DI ROVERE
SPESSORE: 1 cm
PESO SPECIFICO: 720 kg/m3 = 7,2 kN/m3
VOLUME: 0,01 m x 1m x 1m = 0,01 m3
PESO AL METRO Q: 0,01 m3/m2 x 7,2 kN/m3 = 0,072 kN/m2
MASSETTO
SPESSORE: 3 cm
PESO SPECIFICO: 2000 kg/m3 = 20 kN/m3
VOLUME: 0,03 m x 1m x 1m = 0,03 m3
PESO AL MQ: 0,03 m3/m2 x 20 kN/m3 = 0,6 kN/m2
ISOLANTE IN LANA DI VETRO
SPESSORE: 4 cm
PESO SPECIFICO: 20 kg/m3 = 0,2 kN/m3
VOLUME: 0,04 m x 1m x 1m = 0,04 m3
PESO AL METRO Q: 0,04 m3/ m2 x 0,2 kN/m3 = 0,008 kN/m2
INTONACO
SPESSORE: 1 cm
PESO SPECIFICO: 1800 kg/m3 = 18 kN/m3
VOLUME: 0,01 m x 1 m x 1 m = 0,01 m3
PESO AL METRO Q: 0,01 m3/m2 x 18 kN/m3 = 0,18 kN/m2
Qp = (0,072 + 0,6 + 0,008 + 0,18 + 0,5 + 1) = 2,36 kN/m2
(Dove 0,5 è il contributo degli impianti e 1 quello dei tramezzi)
Qa = 2 kN/m2 Valore scelto in quanto legato all’ambiente residenziale.
Il valore di carico da utilizzare per il progetto della trave non è dato dalla sola somma Qs+Qp+Qa: i valori trovati devono ora essere moltiplicati per i rispettivi coefficienti stabiliti dalla normativa (1,3;1,5;1,5); i loro risultati poi andranno sommati e daranno come risultato Q totali /m2 ovvero il carico di progetto ma relativo ad 1m2 di solaio. Per ottenere Qu /ml (ovvero il carico che agisce su un metro lineare di trave) sarà sufficiente moltiplicare Q totali /m2 per la misura dell’interasse:
Qu = ( 4,199 + 3,54 + 3 ) x 3,5 = 37,59 kN/m
Passiamo ora al calcolo del Momento Massimo Flettente della trave considerata.
Quest’ultima è una trave doppiamente appoggiata e quindi la formula del Momento risulta essere: ql2/8.
Mmax = [37,59 kN/m x (7 m)2] / 8 = 230,22 kN/m
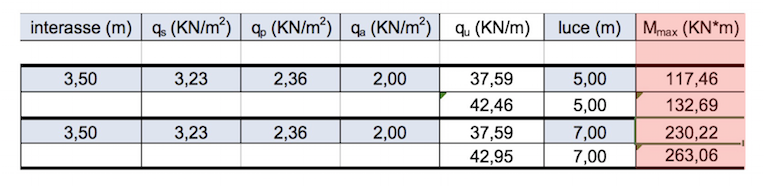
Per il cemento armato avrò due tensioni di progetto essendo un materiale non omogeneo, una per l’acciaio fyd dove y sta per yield ossia snervamento,e una per il calcestruzzo fcd.
La tensione di progetto per l’acciaio che deve resistere a trazione si calcola cosi:
Fyd = fyk / γs
dove fyk rappresenta la tensione caratteristica di snervamento dell’acciaio che da normativa equivale a 450 N/mm2 per quanto riguarda i ferri impiegati nel cls armato ,mentre γs
rappresenta il coefficiente di sicurezza dell’acciaio pari a 1,15.
Fyd = 450 x 1,15 = 391,30 N/mm2
La tensione di progetto per il calcestruzzo è data dalla resistenza caratteristica del cls a resistere a compressione:
Fcd = αcc (fck/γC)
dove fck è la resistenza caratteristica a compressione del calcestruzzo data dal tipo di cls scelto, e in questo caso è 50 N/mm2; αcc è un coefficiente di riduzione pari a 0,85 e γC è il coefficiente di sicurezza per il calcestruzzo pari a 1,5.
Fcd = 0,85 x ( 50/1,5) = 28,33 N/mm2
la tabella excel tiene inoltre conto di un altro coefficiente essendo il calcestruzzo un materiale non omogeneo, il COEFFICIENTE DI OMOGENEIZZAZIONE: n=15
β = fcd/ (fcd + (fyd/n) = 0,52
r = √2/fcd(1-β/3) x β = 2,16
Ora per trovare Hmin della sezione trave ho bisogno di:
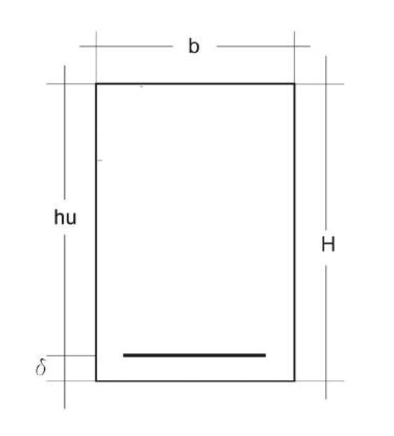
b = 30 cm
in questo modo mi ricavo hu che è l’altezza utile della sezione reagente in calcestruzzo e si trova al di sopra dell’armatura
hu = r √Mmax/b = 25,34 cm
δ= 4 cm (parte sotto del cls maggiormente sollecitata
in questo modo arrivo a calcolarmi Hmin
Hmin = hu + δ = 29,34 cm
Ho trovato ora l’altezza minima che deve avere la mia sezione rettangolare di base 30 cm, dopodiché ingegnerizzo per sicurezza l’altezza a H = 50 cm
VERIFICA
Aggiungo adesso al totale del Qu anche il peso unitario della trave:
(0,30 x 0,55 x 1) m3/m2 x 25 kN/m2 = 4,125 kN/m
lo moltiplico poi per il coefficiente di sicurezza 1,3: 4,125 x 1,3 = 5,36 kN/m2
e lo vado a sommare al mio Qu : 5,36 + 37,59 = 42,95 kN/m2
la tabella excel mi ricalcola l’altezza: la sezione 30x50 cm è stata VERIFICATA.

Abbiamo inoltre verificato la struttura su Sap2000; qui di seguito il diagramma che evidenzia i momenti flettenti:
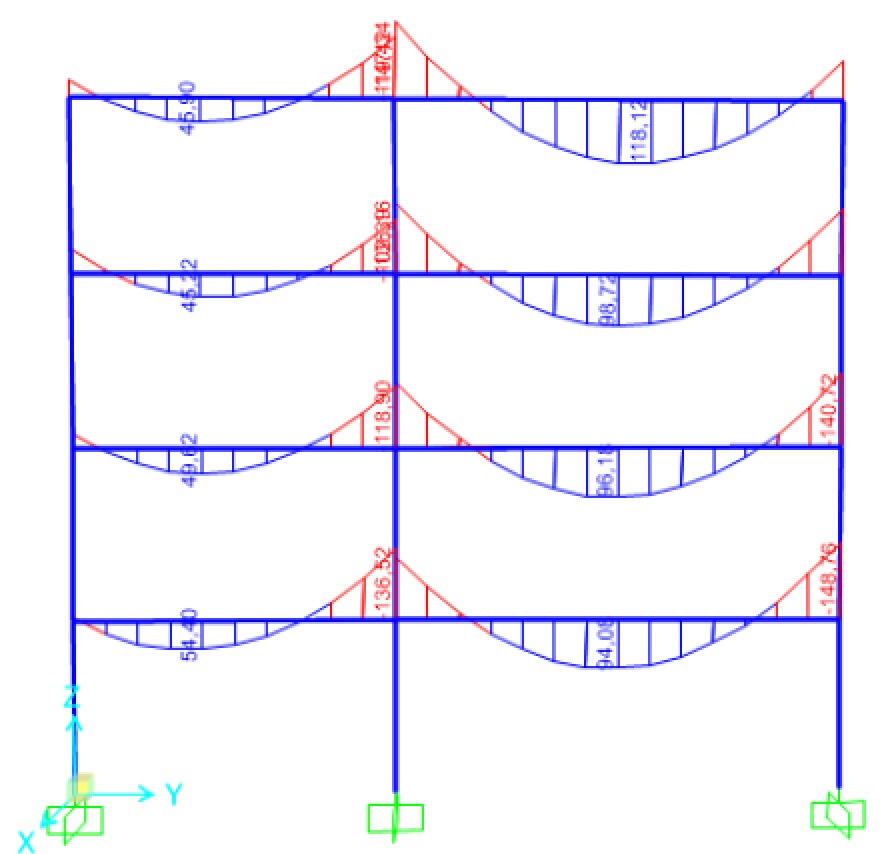
DIMENSIONAMENTO PILASTRO
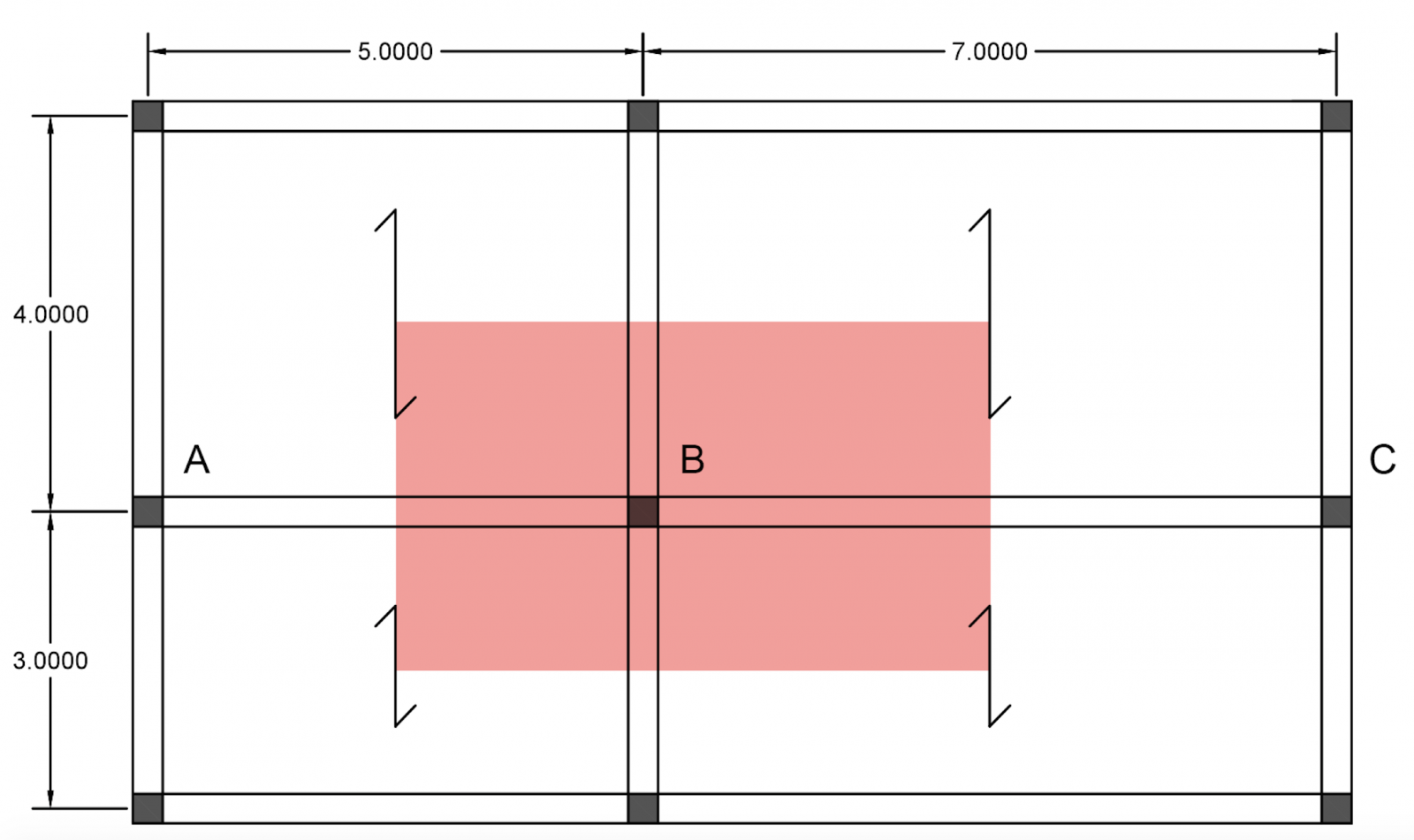
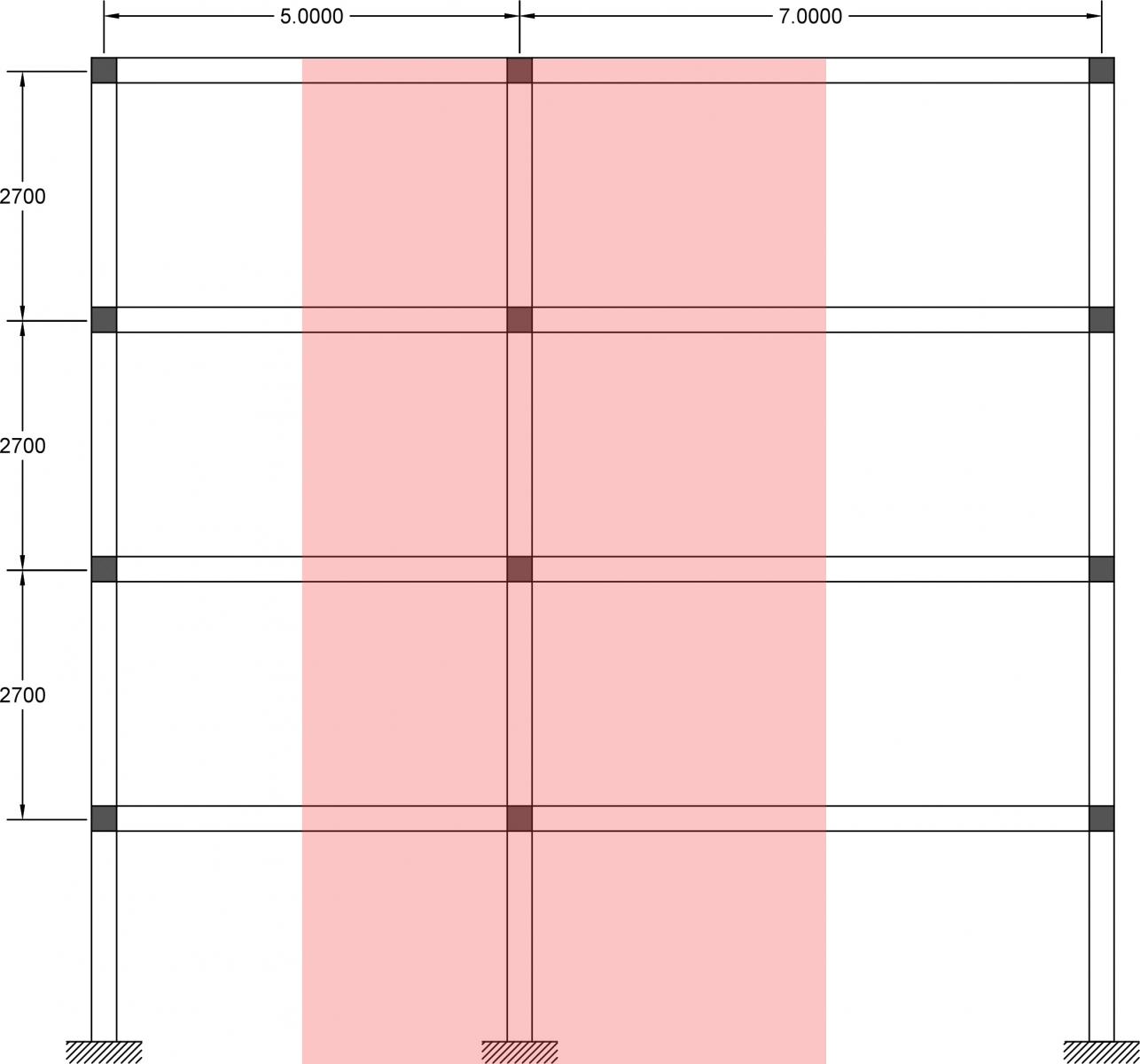
Seguendo ora i valori sopra elencati, inserisco nella tabella excel i dati a mia disposizione:

La tensione di progetto per il calcestruzzo è data dalla resistenza caratteristica del cls a resistere a compressione:
fcd = αcc (fck/γc)
dove fck è la resistenza caratteristica a compressione del calcestruzzo data dal tipo di cls scelto, e in questo caso è 50 N/mm2; αcc è un coefficiente di riduzione pari a 0,85 e γC è il coefficiente di sicurezza per il calcestruzzo pari a 1,5.
fcd = 0,85 x ( 50/1,5) = 28,33 N/mm2
Trovo ora L’area minima e la base minima:
Amin = N/fcd = 368,6753 cm2
Prendo ora in considerazione i valori del modulo di elasticità E, il coefficiente β avente un valore legato alla tipologia di vincoli a cui è soggetto il pilastro e l’altezza I del pilastro per definirne la snellezza λ, il raggio di inerzia minimo ρmin e la base minima che il pilastro dovrà avere:
λ = π √E/fcd = 85,52847
ρmin = (β x I) / λ = 3,156844 cm
bmin = ρmin x √12 = 10,93563 cm
Ingegnerizzo i valori minimi ricavati per ottenere le due dimensioni del pilastro = 30 x 50 cm.
Non ci resta che calcolare:
Adesign =b*h = 1500 cm2
Idesign =(h*b3)/12 = 112500 cm4
VERIFICA
Il pilastro in cls armato è sottoposto, oltre che a compressione, a presso-flessione, poiché il nodo trave-pilastro è realizzato da un incastro (il che trasmette momento), per evitare fenomeni di instabilità devo verificare che σmax sia minore o uguale a fcd.
A questo punto σmax = N/A + Mt /Wmax ≤ fcd ? Sì, 7,98 ≤ 28,33
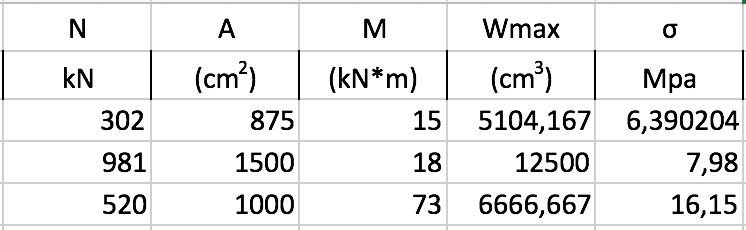
Abbiamo inoltre verificato la struttura su Sap2000; qui di seguito il diagramma che evidenzia lo sforzo assiale:
DIMENSIONAMENTO TRAVE
ACCIAIO
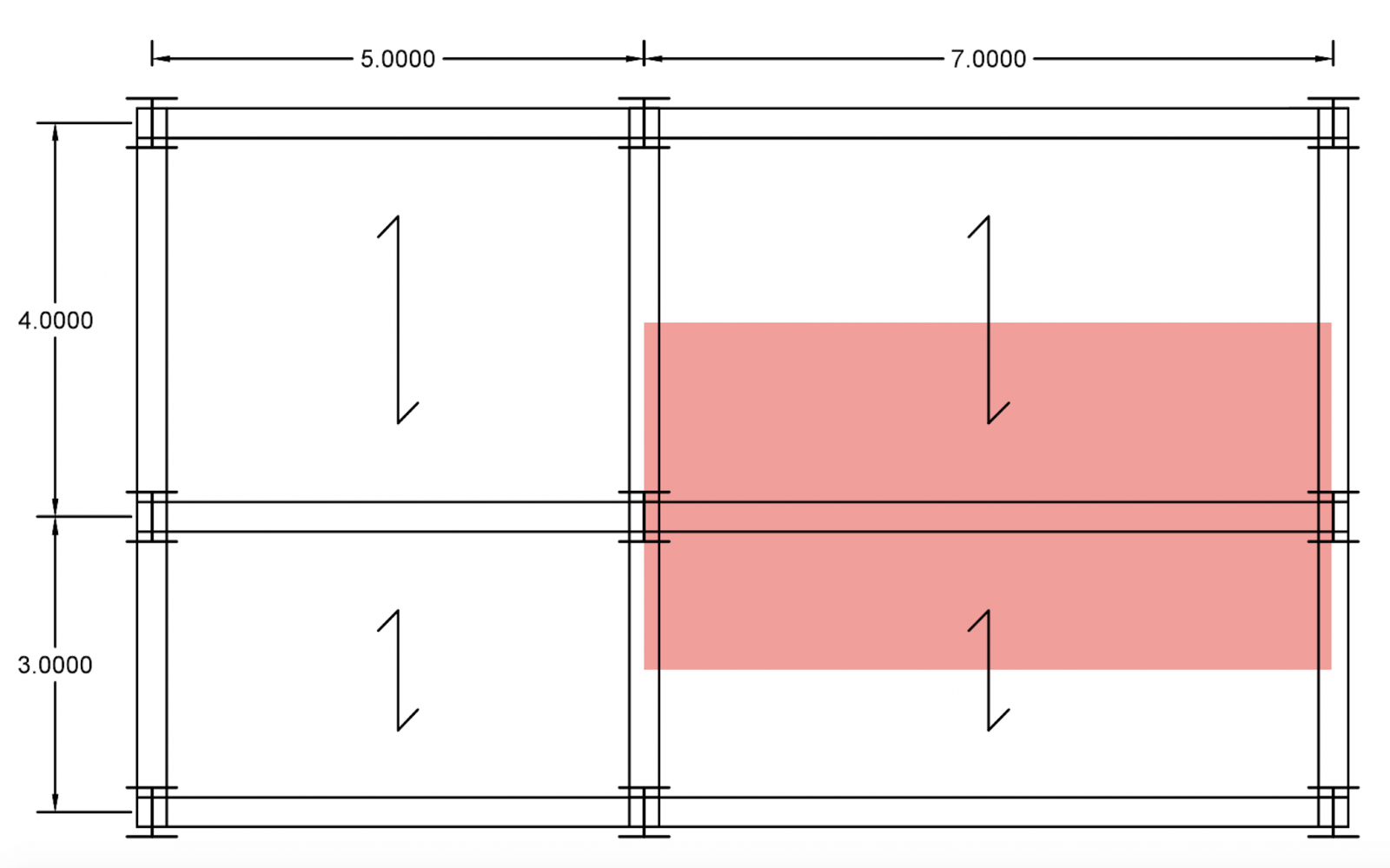
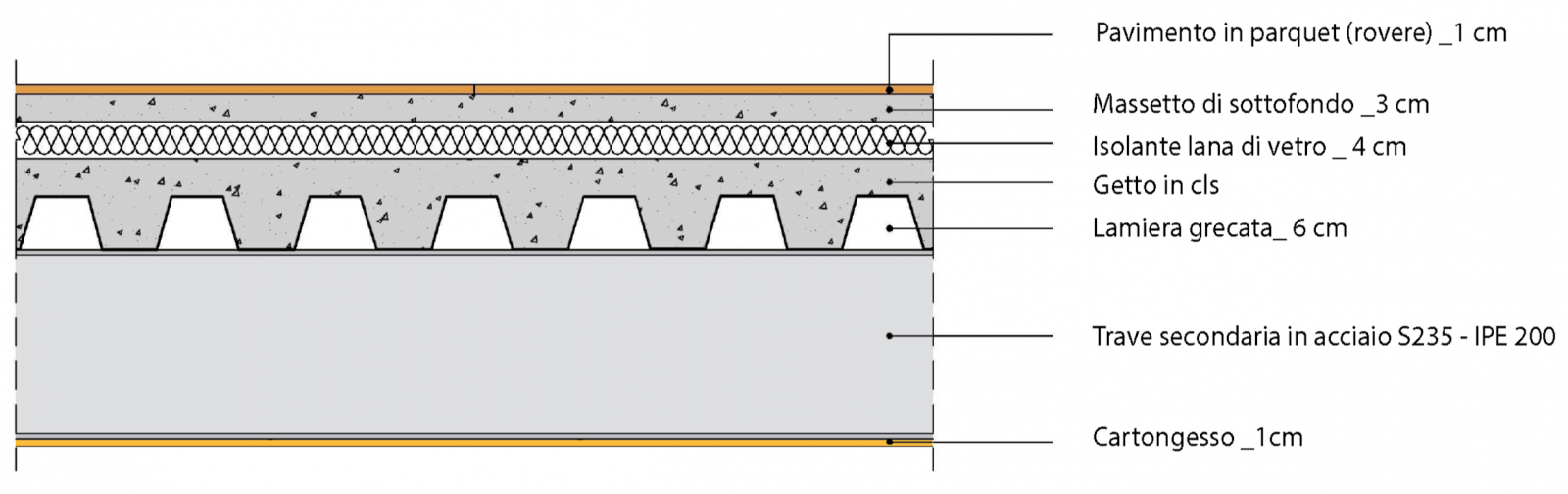
Per questo tipo di tecnologia costruttiva è stato scelto un solaio in lamiera grecata. Verrà calcolato tutto per una porzione di solaio pari a 1 m2.
ANALISI:
Il carico strutturale dipende dal peso delle travi secondarie, della lamiera recata e della soletta in calcestruzzo.
TRAVETTO IPE200
AREA: 28,5 cm2 = 0,0028 m2
PESO: 22,4 kg/m = 0,224 kN/m3
PESO AL METRO Q = 0,224 kN/m2
GETTO DI CLS
SEZIONE: 0,07 M2
PESO SPECIFICO: 2500 kg/m3 = 25 kN/m3
VOLUME: 0,07 m2 x 1 m = 0,07 m3
PESO AL METRO Q: 0,07 m3/m2 x 25 kN/m3 = 1,75 kN/m2
QS = (0,224 + 1,75) kN/m2 = 1,974 kN/m2
Il carico permanente Qp dipende dal peso del’isolante, del massetto, del pavimento e del rivestimento in cartonassero aggiungendo il peso degli impianti e dei tramezzi.
PAVIMENTO IN PARQUET DI ROVERE
SPESSORE: 1 cm
PESO SPECIFICO: 720 kg/m3 = 7,2 kN/m3
VOLUME: 0,01 m x 1m x 1m = 0,01 m3
PESO AL METRO Q: 0,01 m3/m2 x 7,2 kN/m3 = 0,072 kN/m2
MASSETTO
SPESSORE: 3 cm
PESO SPECIFICO: 2000 kg/m3 = 20 kN/m3
VOLUME: 0,03 m x 1m x 1m = 0,03 m3
PESO AL MQ: 0,03 m3/m2 x 20 kN/m3 = 0,6 kN/m2
ISOLANTE IN LANA DI VETRO
SPESSORE: 4 cm
PESO SPECIFICO: 20 kg/m3 = 0,2 kN/m3
VOLUME: 0,04 m x 1m x 1m = 0,04 m3
PESO AL METRO Q: 0,04 m3/ m2 x 0,2 kN/m3 = 0,008 kN/m2
CARTONGESSO
SPESSORE: 1 cm
PESO SPECIFICO: 9 kN/m3
VOLUME: 0,01 m x 1 m x 1 m = 0,01 m3
PESO AL METRO Q: 0,01 m3/m2 x 9 kN/m3 = 0,09 kN/m2
Qp = (0,072 + 0,6 + 0,008 + 0,09 + 0,5 + 1) = 2,27 kN/m2
(Dove 0,5 è il contributo degli impianti e 1 quello dei tramezzi)
Qa = 2 kN/m2 Valore scelto in quanto legato all’ambiente residenziale.
Il valore di carico da utilizzare per il progetto della trave non è dato dalla sola somma Qs+Qp+Qa: i valori trovati devono ora essere moltiplicati per i rispettivi coefficienti stabiliti dalla normativa (1,3;1,5;1,5); i loro risultati poi andranno sommati e daranno come risultato Q totali /m2 ovvero il carico di progetto ma relativo ad 1m2 di solaio. Per ottenere Qu /ml (ovvero il carico che agisce su un metro lineare di trave) sarà sufficiente moltiplicare Q totali /m2 per la misura dell’interasse:
Qu = ( 2,56 + 3,405 + 3 ) x 3,5 = 31,40 kN/m
Passiamo ora al calcolo del Momento Massimo Flettente della trave considerata.
Quest’ultima è una trave doppiamente appoggiata e quindi la formula del Momento risulta essere: ql2/8.
Mmax = [31,40 kN/m x (7 m)2] / 8 = 192,32 kN/m

Ora sceglieamo il valore caratteristico di snervamento per l’acciaio fyk che mi individua la classe di resistenza del materiale , in questo caso scelgo una resistenza di 235 MPa.
Mi calcolo così la tensione di progetto fd ( tensione ammissibile) dividendo fyk per un il coefficiente di sicurezza per la resistenza delle membrature e la stabilità, γs = 1,05 :
Fd = 235/1.05= 223,81 N/mm2
Mi calcolo infine il MODULO DI RESISTENZA A FLESSIONE Wx,min, per poi andare a scegliere il profilato appropriato sulla tabella dei profili in acciaio.
Wx,min = Mmax/fd = 859,30 cm3
La tabella di calcolo mi ha ora trovato il Wx,min cioè il valore minimo che la sezione che sceglierò dovrà avere affinchè nessuna fibra del materiali superi la tensione di progetto.
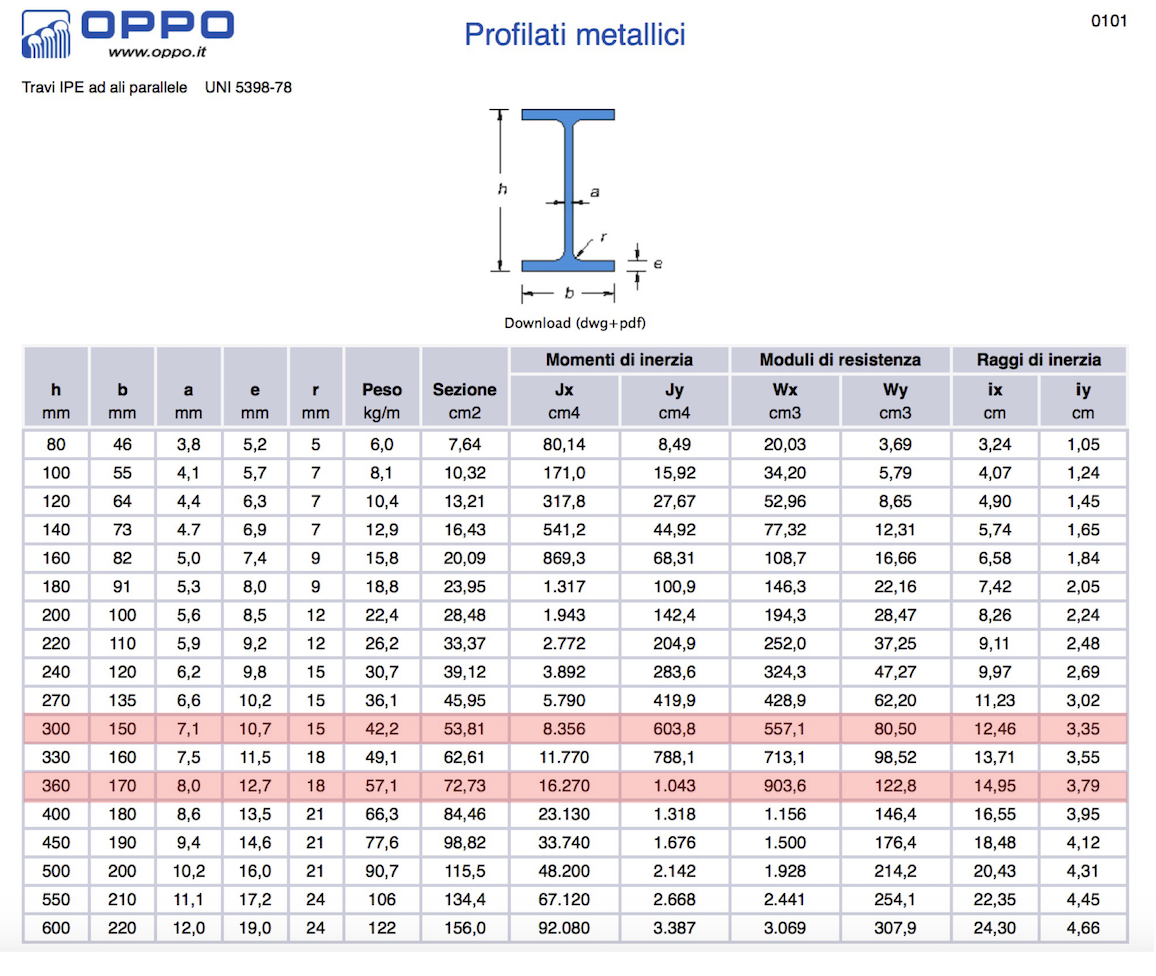
Nella tabella dei profili metallici scelgo un profilo adatto che abbia un modulo di resistenza a flessione Wx maggiore di quello da me trovato: SCEGLIAMO QUINDI UNA IPE 360.

Qui di seguito la tabella di riferimento per la scelta del profilato IPE:
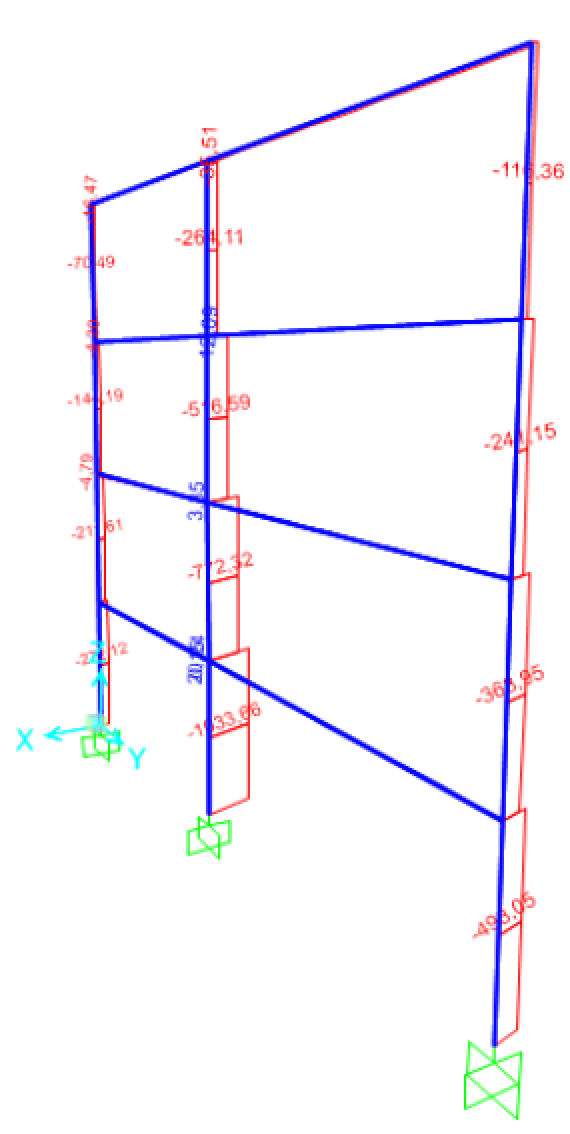
Abbiamo inoltre verificato la struttura su Sap2000; qui di seguito il diagramma che evidenzia i momenti flettenti:
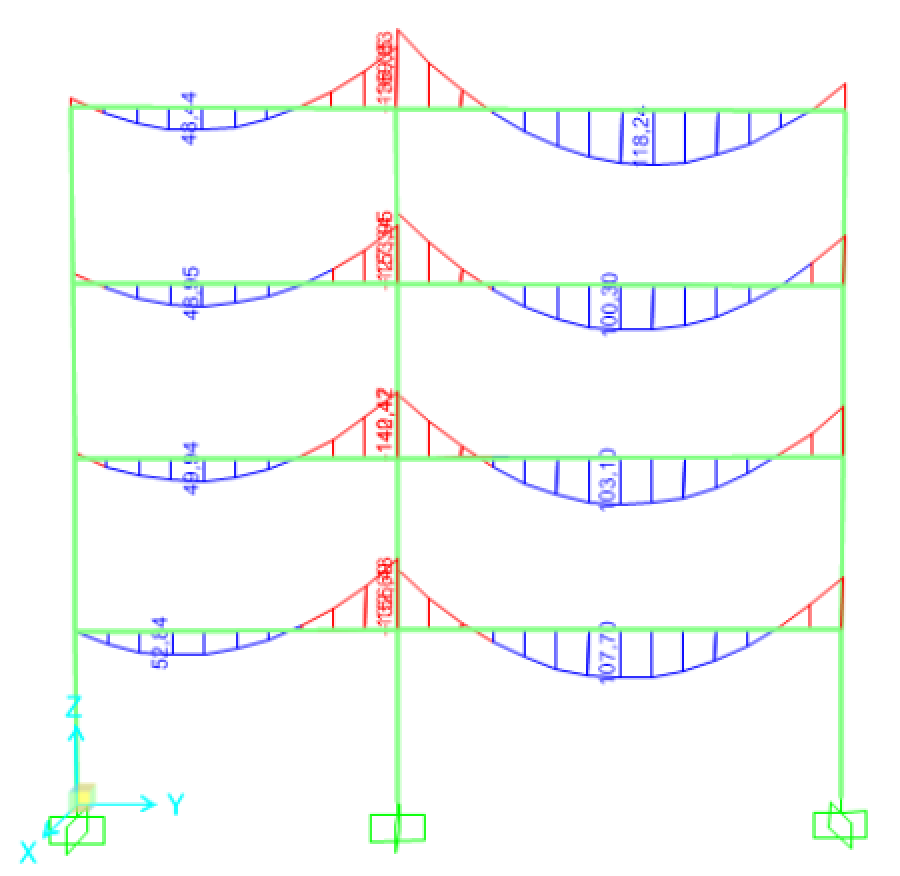
DIMENSIONAMENTO PILASTRO
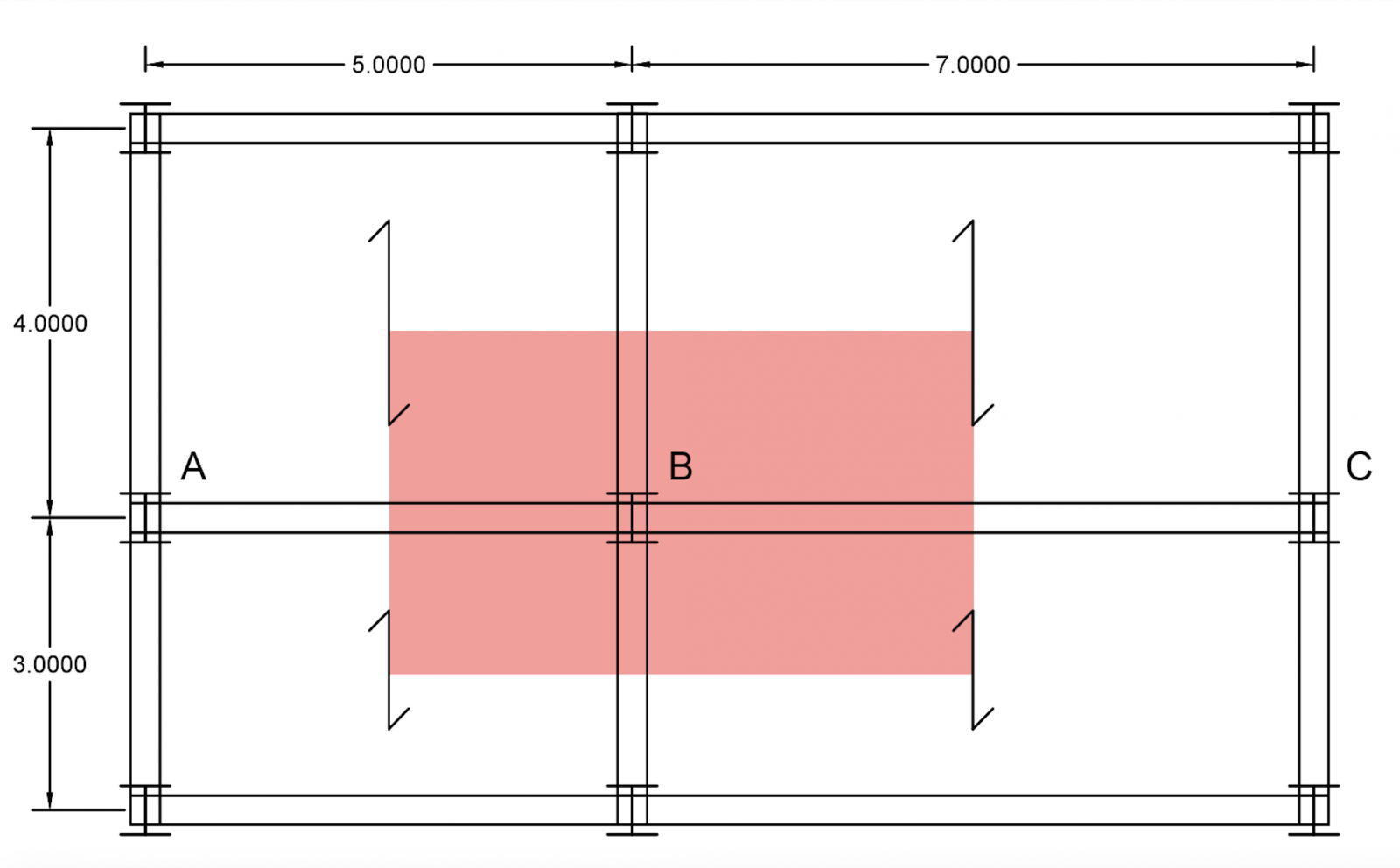

Seguendo i valori sopra elencati, inserisco i dati a mia disposizione nella mia tabella excel:

Scelgo il tipo di acciaio da utilizzare per il pilastro e definisco quindi la sua tensione caratteristica di snervamento fyk; moltiplico questo valore per γm coefficiente parziale di sicurezza per trovare il valore della tensione di progetto fyd; trovo adesso l'Amin:
Amin = N/fyd
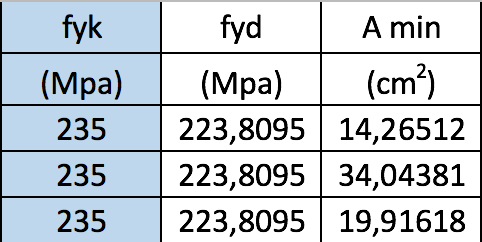
λ* = √(E/fyd)
ρmin = β l/ λ*
Imin = Aρmin2 (ricavo dunque il momento di inerzia minimo in funzione del raggio di inerzia minimo)
Attraverso la tabella dei profili HEA ricavo i valori di Adesign , Idesign e ρmin maggiori di quelli minimi ottenuti, il cui profilo risulta essere un HEA160.
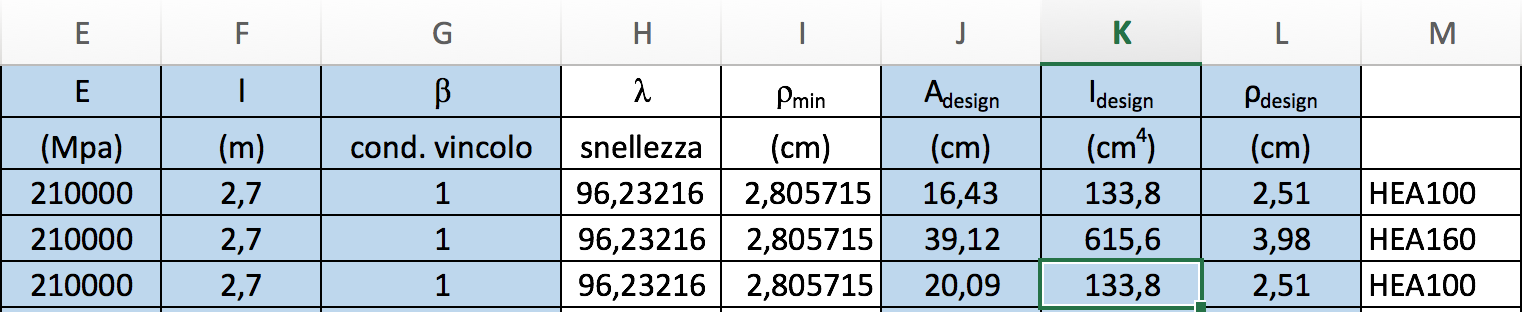
Abbiamo inoltre verificato la struttura su Sap2000; qui di seguito il diagramma che evidenzia lo sforzo assiale:
DIMENSIONAMENTO TRAVE
LEGNO

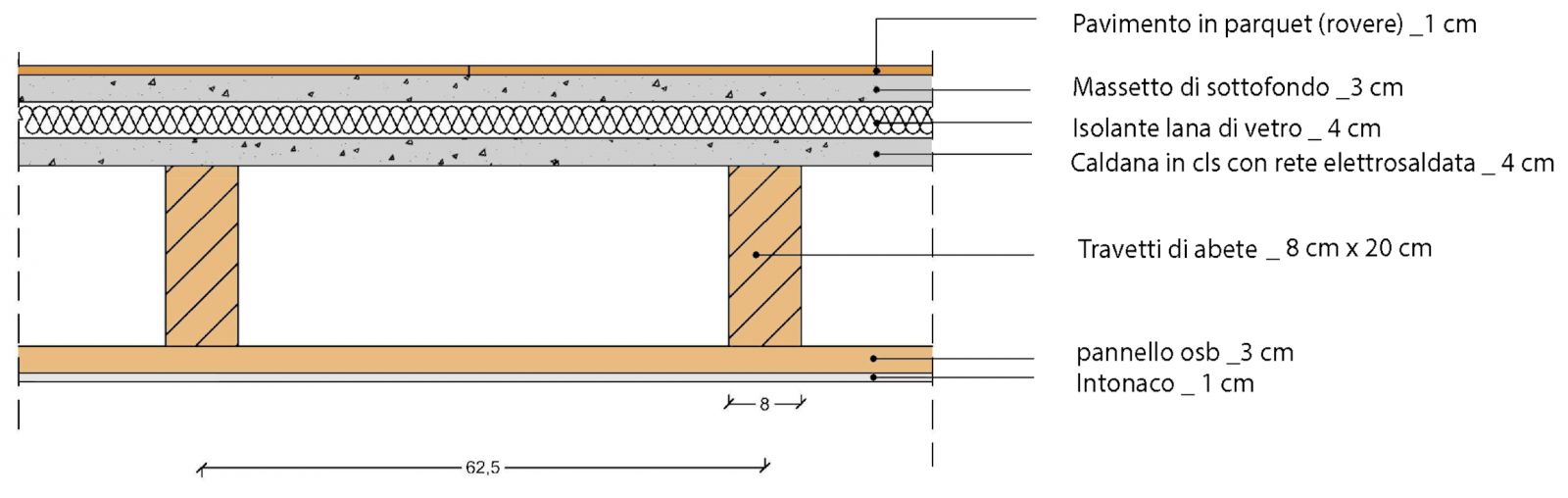
Per questo tipo di tecnologia costruttiva è stato scelto un solaio in travetti e pannelli OSB. Verrà calcolato tutto per una porzione di solaio pari a 1 m2
ANALISI:
Il carico strutturale dipende dal peso del travetto in legno d’abete e tavolato oso.
TRAVETTO IN LEGNO D’ABETE:
SEZIONE: 8 cm x 20 cm
PESO SPECIFICO: 550 kg/m3 = 5,5 kN/m3
VOLUME: 0,000256 m3
PESO AL METRO Q = 0,000256 m3/m2 x 5,5 kN/m3 = 0,0014 kN/m2
TAVOLATO IN OSB:
SPESSORE: 3 cm
PESO SPECIFICO: 650 Kkg/m3 = 6,5 kN/m3
VOLUME: 0,03 m x 1 m x 1 m = 0,03 m3
PESO AL METRO Q: 0,03 m3/m2 x 6,5 kN/m3 = 0,195 kN/m2
QS = (2 x 0,195 + 0,0014) kN/m2 = 0,39 kN/m2
Il carico permanente Qp dipende dal peso della caldana, dell’isolante, del massetto, del pavimento, dell’intonaco, aggiungendo il contributo di tramezzi e impianti.
PAVIMENTO IN PARQUET DI ROVERE
SPESSORE: 1 cm
PESO SPECIFICO: 720 kg/m3 = 7,2 kN/m3
VOLUME: 0,01 m x 1m x 1m = 0,01 m3
PESO AL METRO Q: 0,01 m3/m2 x 7,2 kN/m3 = 0,072 kN/m2
MASSETTO
SPESSORE: 3 cm
PESO SPECIFICO: 2000 kg/m3 = 20 kN/m3
VOLUME: 0,03 m x 1m x 1m = 0,03 m3
PESO AL MQ: 0,03 m3/m2 x 20 kN/m3 = 0,6 kN/m2
ISOLANTE IN LANA DI VETRO
SPESSORE: 4 cm
PESO SPECIFICO: 20 kg/m3 = 0,2 kN/m3
VOLUME: 0,04 m x 1m x 1m = 0,04 m3
PESO AL METRO Q: 0,04 m3/ m2 x 0,2 kN/m3 = 0,008 kN/m2
INTONACO
SPESSORE: 1 cm
PESO SPECIFICO: 1800 kg/m3 = 18 kN/m3
VOLUME: 0,01 m x 1 m x 1 m = 0,01 m3
PESO AL METRO Q: 0,01 m3/m2 x 18 kN/m3 = 0,18 kN/m2
CALDANA IN CLS CON RETE ELETTROSALDATA
SPESSORE: 4 cm
PESO SPECIFICO: 2500 kg/m3 = 25 kN/m3
VOLUME: 0,04 m x 1 m x 1 m = 0,04 m3
PESO AL METRO Q: 0,04 m3/m2 x 25 kN/m3 = 1 kN/m2
Qp = (1+ 0,008 + 0,6 + 0,072 + 0,18 + 0,5 + 1) = 3,36 kN/m2
(Dove 0,5 è il contributo degli impianti e 1 quello dei tramezzi)
Qa = 2 kN/m2 Valore scelto in quanto legato all’ambiente residenziale.
Il valore di carico da utilizzare per il progetto della trave non è dato dalla sola somma Qs+Qp+Qa: i valori trovati devono ora essere moltiplicati per i rispettivi coefficienti stabiliti dalla normativa (1,3;1,5;1,5); i loro risultati poi andranno sommati e daranno come risultato Q totali /m2 ovvero il carico di progetto ma relativo ad 1m2 di solaio. Per ottenere Qu /ml (ovvero il carico che agisce su un metro lineare di trave) sarà sufficiente moltiplicare Q totali /m2 per la misura dell’interasse:
Qu = ( 0,507 + 5,04 + 3) x 3,5 = 29,91 kN/m
A questo punto posso calcolarmi il momento massimo Mmax agente sulla trave avendo il carico lineare Qu, la luce che copre la mia trave che è 7 e sapendo che il momento massimo di una trave appoggiata è ql2/8.

Mmax = Qu x l2/8= 183,23 kN*m
Per calcolare la TENSIONE DI PROGETTO Fd per quanto riguarda il legno abbiamo bisogno di alcuni valori:
In fase progettuale si è scelto un legno lamellare con resistenza meccanica fmk pari a 27 Mpa.
γm (coefficiente di sicurezza del materiale) = 1,45
Kmod: è un coefficiente che riduce i valori della resistenza che tiene conto della durata del carico e delle condizioni di umidità e cambia a seconda del materiale prescelto , nel nostro caso: classe di servizio 2, classe di durata del carico media = 0.80
Inserendo questi dati nella tabella di calcolo mi ricavo Fd = Kmod x fmk / γm
Quindi il nostro fd = 14,90 N/mm2
Rimane ora da inserire nel foglio excel la base b = 26 cm ipotizzata per trovare l’altezza minima della trave di legno che era l’unica incognita nel nostro progetto.
L’altezza minima viene 53,28 cm e con una ingegnerizzazione arrivo ad un altezza della trave in legno di 55 cm.

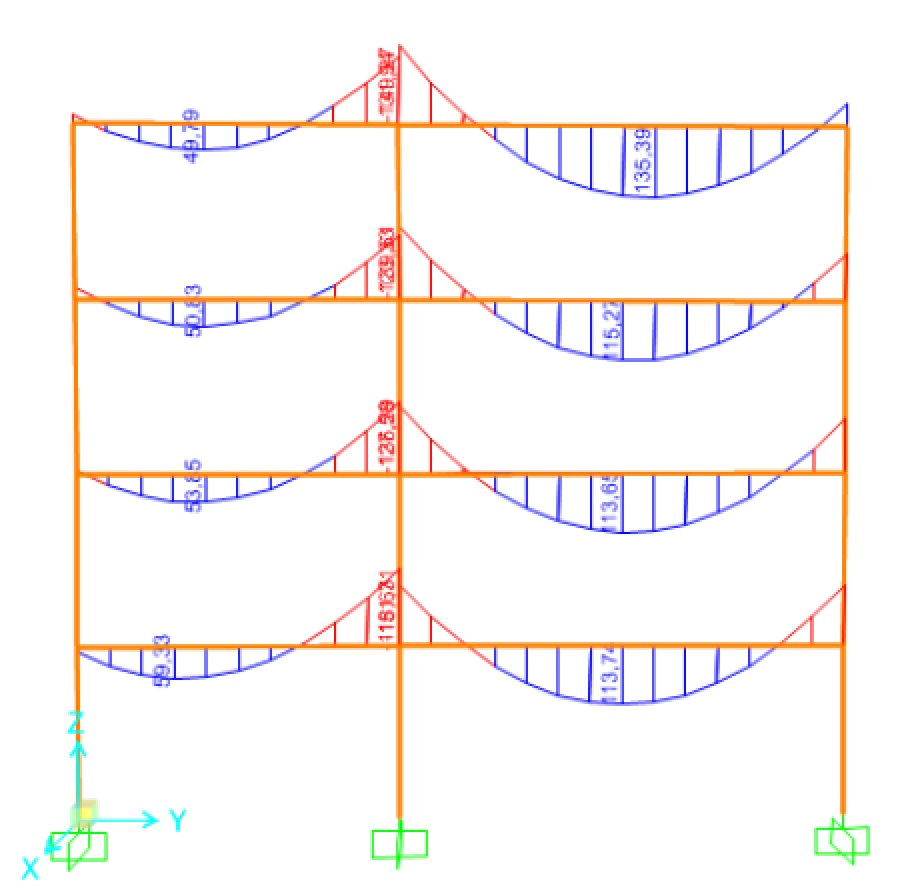
Abbiamo inoltre verificato la struttura su Sap2000; qui di seguito il diagramma che evidenzia i momenti flettenti:
DIMENSIONAMENTO PILASTRO


Seguendo i valori sopra elencati, inserisco i dati a mia disposizione nella mia tabella excel:

Procedo ora con il pre-dimensionamento della sezione del pilastro a partire dalla resistenza del materiale e ottenendo quanto vale Amin.
fmk = resistenza caratteristica a flessione nella direzione delle fibre (dipende dal materiale)
kmod = coefficiente di durata del carico (fornito dalla normativa)
γm = coefficiente di sicurezza
Ottengo così la tensione ammissibile fd = fmk x kmod / γm e quindi l'area minima necessaria alla sezione affinché il materiale non giunga a rottura.
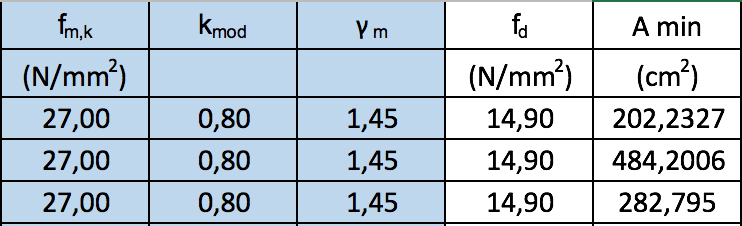
Prendo ora in considerazione i valori del modulo di elasticità E, il coefficiente β avente un valore legato alla tipologia di vincoli a cui è soggetto il pilastro e l’altezza I del pilastro per definirne la snellezza λ, il raggio di inerzia minimo ρmin e la base minima che il pilastro dovrà avere:
λ = π √E/fcd = 72,80346
ρmin = (β x I) / λ = 3,708615 cm
bmin = ρmin x √12 = 12,84702 cm
Ingegnerizzo i valori minimi ricavati per ottenere le due dimensioni del pilastro = 20 x 50 cm.
Non ci resta che calcolare:
Adesign =b*h = 1000 cm2
Idesign =(h*b3)/12 = 33333,33 cm4
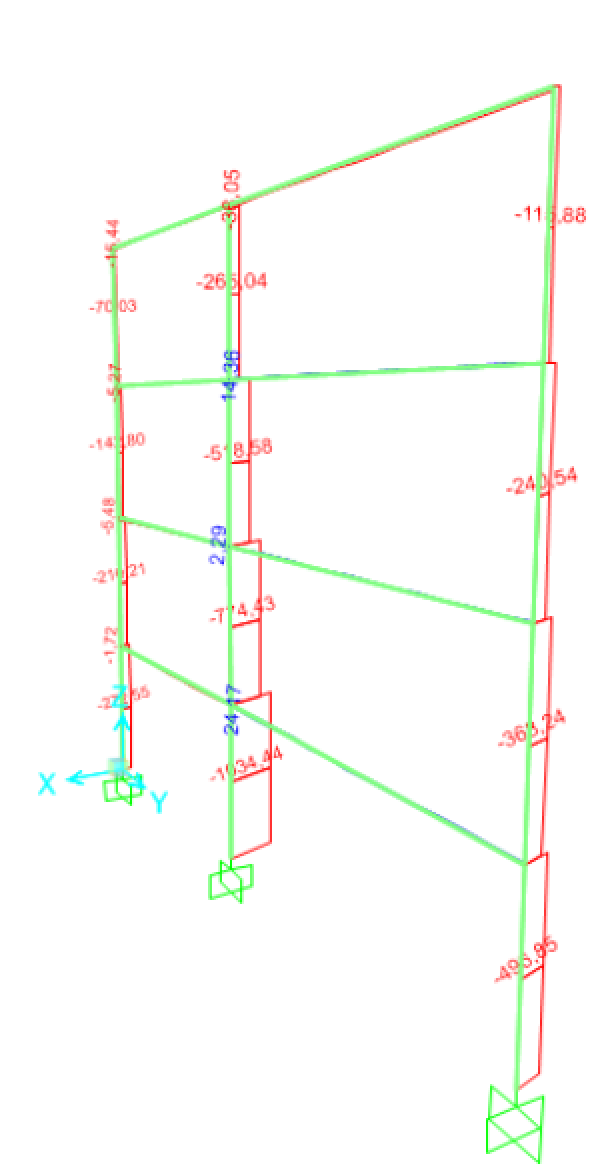
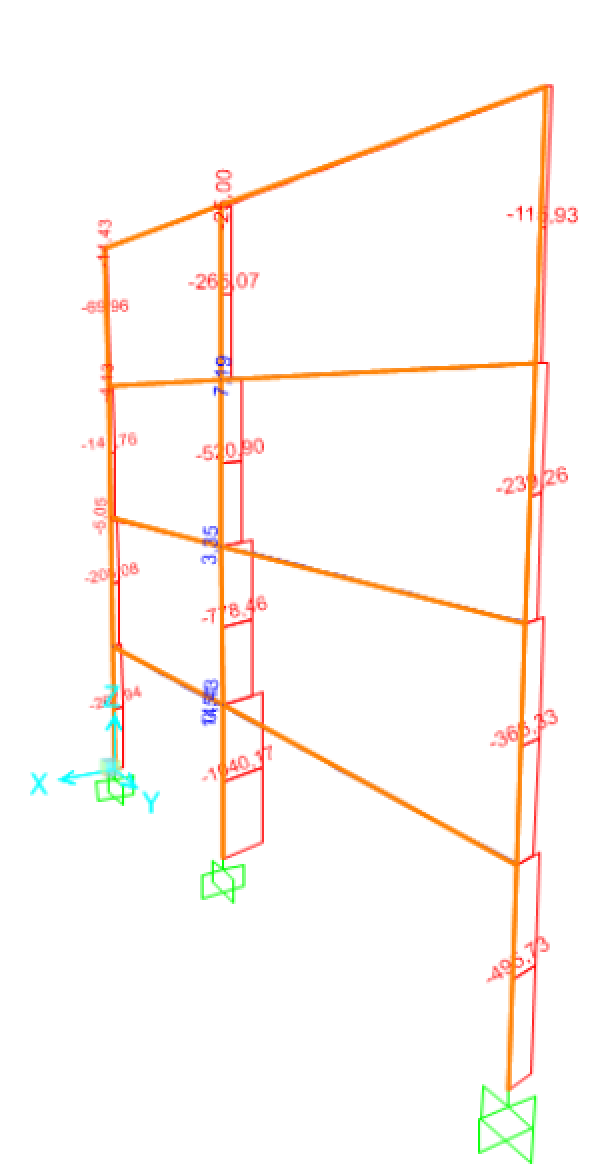
Abbiamo inoltre verificato la struttura su Sap2000; qui di seguito il diagramma che evidenzia lo sforzo assiale:
(Lavoro svolto in gruppo con Italo Millozzi e Angela Messina)
