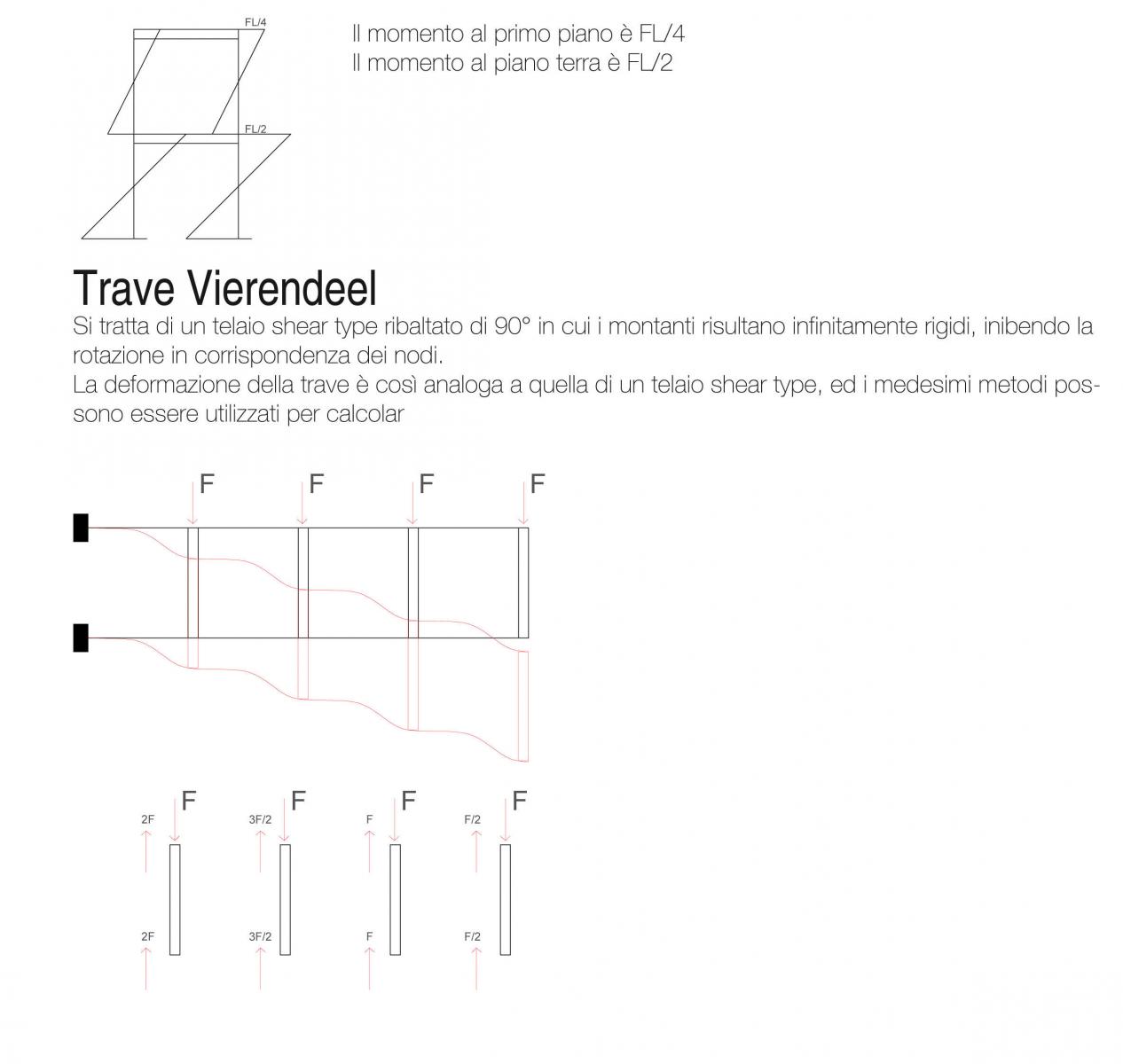
Esercitazioni

TRAVATURE RETICOLARI

Definizione: aste rettilinee, collegate alle estremità mediante cerniere

 

 

Le travi reticolari sono sistemi di travi soggette prevalentemente a forze di tipo assiale, le travi che compongono le strutture reticolari sono chiamate "aste", le quali sono collegate tra alle estremità tramite nodi cerniera, oppure nodi incastro.

Se le aste sono incernierate nei nodi e se le forze esterne agiscono solo nei nodi, l' unica sollecitazione presente è solo di sforzo normale. Se invece vi sono forze esterne agenti lungo le aste, queste risultano anche inflesse. Se però le forze prevalenti sono quelle applicate ai nodi allora prevarranno le forze normali sulle azioni flettenti.

 

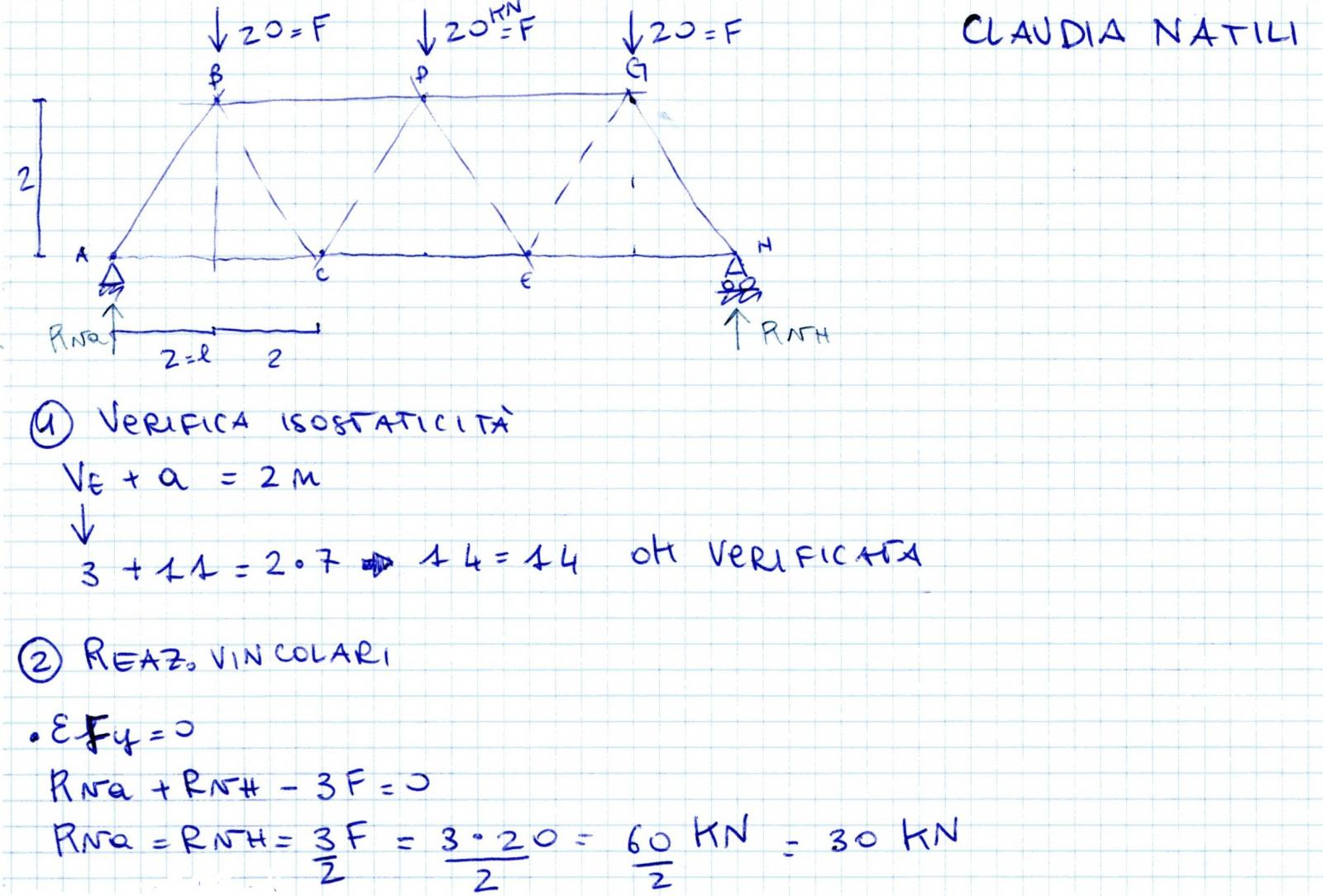
TRAVE RETICOLARE SIMMETRICA

1) Verifica dell' isostaticità: Ve+ a=2n ---- 3+11=14 !!!!!OK VERIFICATO!!!

Ve= gradi di vincolo esterni, in questo caso sono 2+1, ovvero 2 gradi da parte della cerniera e 1 da parte del carrello                        

a=numero delle aste, ovvero 11

n= numero dei nodi ovvero 7

2) Calcolo delle reazioni vincolari è il secono step...

 

3) Calcolo delle tensioni_METODO DI RITTER O DELLE SEZIONI

Una travatura reticolare generata a partire da un triangolo iniziale presenta la proprietà di poter essere tagliata da una sezione ideale, che divida la struttura integralmente in due parti sezionando solo tre aste non concorrenti nello stesso punto.
Si può quindi disegnare lo schema isolato di una delle due porzioni.

Prima sezione _Per cui nel primo tratto che seziono calcolo il Momento nel punto C per trovare N1, il Momento nel punto B per trovare N3 e con la sommatoria delle forze in direzione y trovo N2...

Seconda sezione_ con il momento nel punto D trovo N5, e con l' equilibrio alla traslazione in y trovo N6, come si può vedere l' asta N5 è la più sollecitata è pari a 50 kn...

Il secondo metodo per calcolare le sollecitazioni delle aste su una trave reticolare è il METODO DEI NODI ovvero:

Tale procedimento richiede di individuare un nodo semplice, definito come nodo in cui convergono due aste e di risolverlo mediante le due equazioni di equilibrio del nodo stesso. Si procede quindi nell’isolare un nodo della struttura reticolare tagliando le aste che vi convergono. Si esplicitano quindi gli sforzi normali trasmessi dalle aste al nodo e le eventuali forze esterne. Si scrivono infine le equazioni di equilibrio per il nodo in esame.
Poiché le forze sono convergenti al nodo, l’equazione di equilibrio dei momenti rispetto al nodo stesso è identicamente soddisfatta (ΣMnodo=0). Nel caso piano si hanno pertanto a disposizione per ogni nodo solo le rimanenti due equazioni di equilibrio: ΣFx,nodo=0 ΣFy,nodo=0.

Controprova con SAP_ Reazioni Vincolari...

Deformazione...

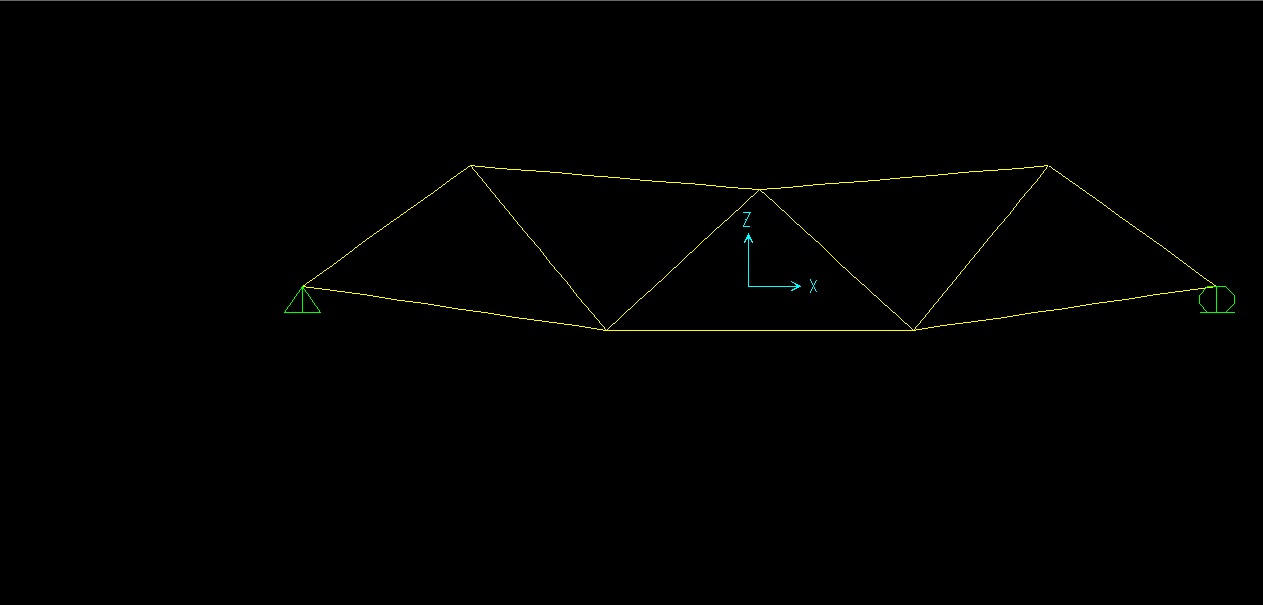
Sforzi assiali sulle aste...

 

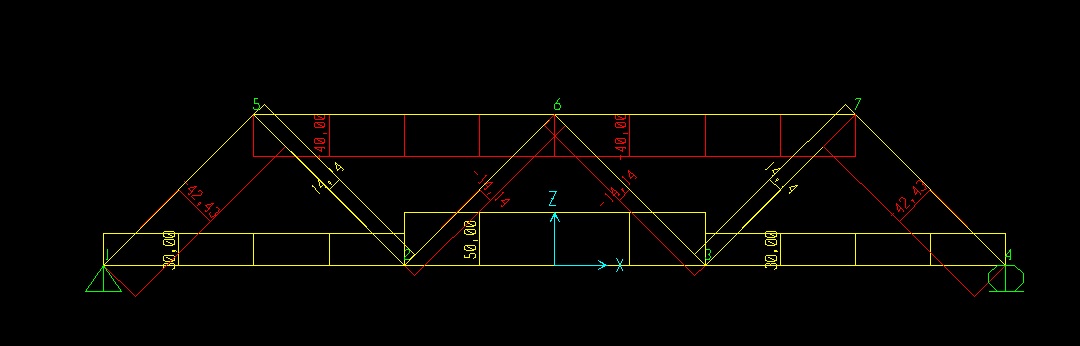
TRAVE RETICOLARE ASIMMETRICA

La trave asimmetrica, per sua natura, ci impone di calcolare tutte le aste della trave in quanto i risultati degli sforzi normali su tutta la trave saranno differenti per ogni asta.

Differente è la trave simmetrica dell' esercizio precedente che avendo un asse di simmetria verticale permette di calcolarci solo un metà degli sforzi normali della trave in quanto i risultati degli sforzi normali dell' altra metà saranno, per natura della trave, identici.

 

1)Verifica dell' isostaticità: Ve+ a= 2n

3+11= 2x7---->14=14 OK è VERIFICATO!!!LA TRAVE è ISOSTATICA!!!

 

2)Calcolo delle reazioni vincolari:

Ipotizzo i versi delle reazioni vincolari (frecce rosse) Rua, Rva e Rud, essendo le mie incognite faccio l' equilibrio alla traslazione orizzontale, ∑ Fx=0 in cui trovo che Rua e Rud sono uguali (di modulo ma con segno opposto!!); con la traslazione verticale ∑ Fy=0 trovo che Rva è uguale a 2 volte F ovvero 20 kn; calcolandomi il momento nel punto A trovo che Rud è uguale a 3Fl/H= 30 kn=Rua=Rud.

I versi che ho ipotizzato per le reazioni vincolari sono giusti!!!!

 

Ho fatto anche la controprova con SAP

 

 

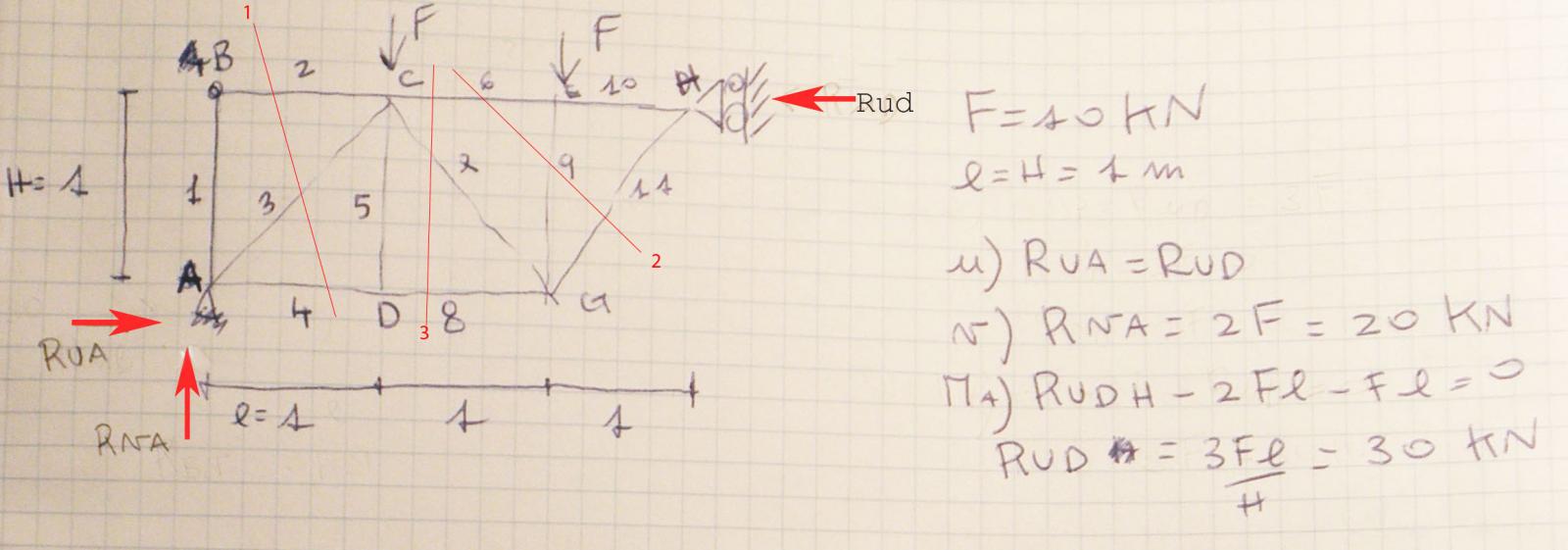
3)Calcolo delle tensioni:

 

-Sezione di ritter n°1_ Con la ∑ Mc=0 trovo N4= -10 kn, il verso che ho ipotizzato è sbagliato per cui l' asta è compressa

                              _ Con la ∑ Ma=0 trovo che l' asta N2= 0 per cui è un' asta scarica

                              _ Con la ∑ Fy=0 trovo che N3= -20√2, il verso ipotizzato errato per cui l' asta è compressa.

 

 

 

-Equilibrio al nodo H_ Con la ∑ Fx=0 trovo che N10= -30 kn, verso errato asta compressa

                             _ Con la ∑ Fy=0 trovo che N11=0 l' asta è scarica

 

 

 

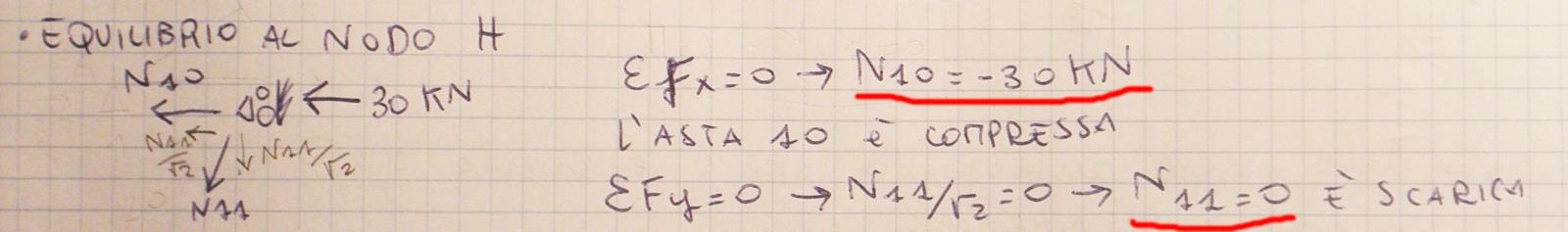
Sezione di ritter n°2_ Con la Con la ∑ Mg=0 trovo N6= -30 kn, verso errato asta compressa

                              _ Con la ∑ Me=0 confermo che l' asta 11 è scarica N11=0

                              _ Con la ∑ Fy=0 trovo che N9= -10 kn verso errato asta compressa

 

 

 

Sezione di ritter n°3_ Con la ∑ Mc=0 trovo N8=-10kn verso errato asta compressa

                             _ Con la ∑ Fy=0 trovo N7= F√2, verso giusto!! asta 7 tesa

 

 

 

 

 

 

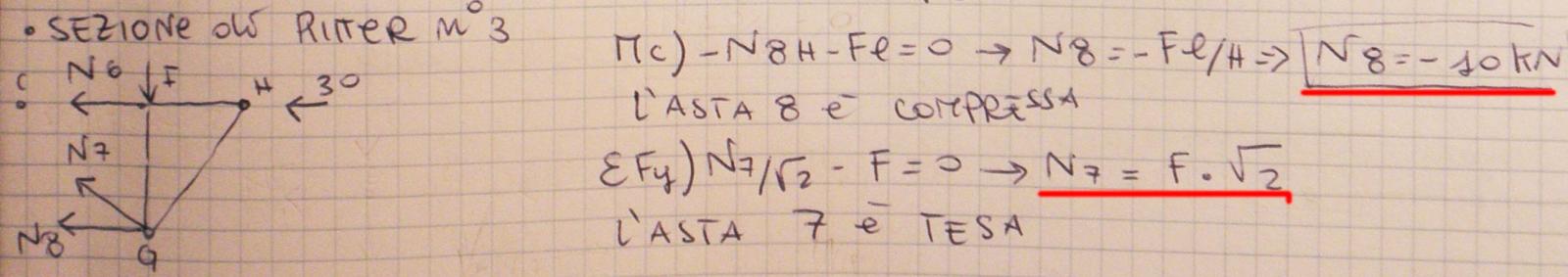
Equilibrio al nodo B_ Con la ∑ Fx=0 trovo che N2= 0, asta scarica ipotesi riconfermata

                            _ Con la ∑ Fy=0 trovo che N1=0, asta scarica

 

 

 

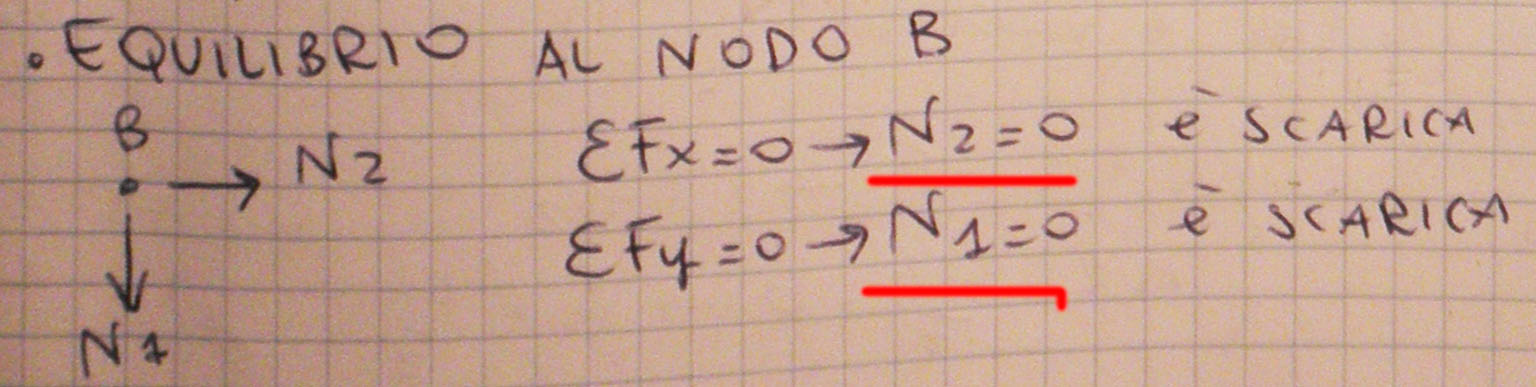
Equilibrio al nodo D_ Con la ∑ Fy=0 trovo che N5= 0, asta scarica

 

 

 

Con sap èchiaro vedere la deformazione.....

 

 

 

E gli sforzi assiali sulle singole aste...

 

 

 

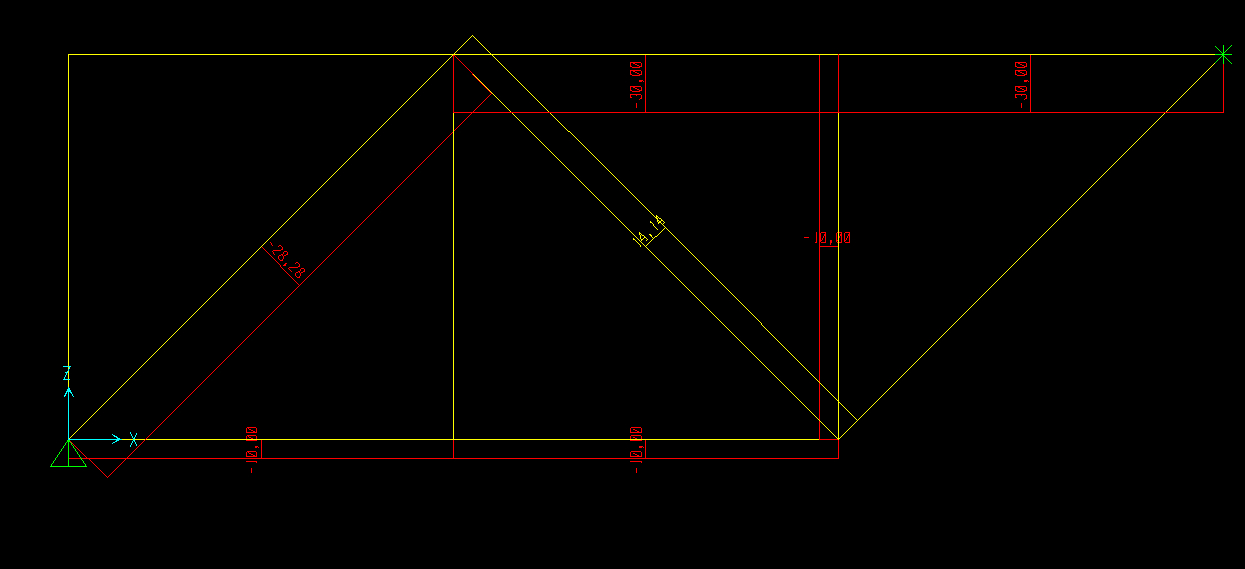
Esercitazione_Portale a 3 cerniere con carico distribuito lungo l' asse X

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

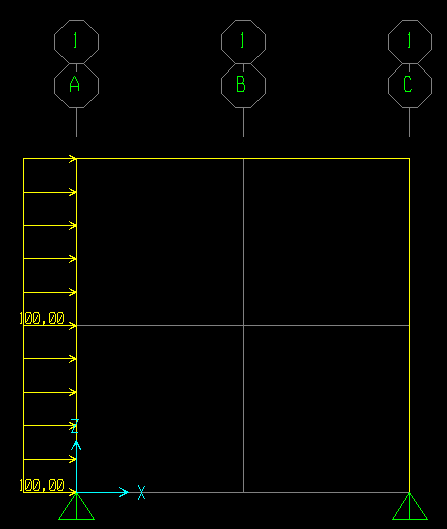
Dati

q= 100 kN/m

h=10m

l=5m

Ad occhio vediamo che la struttura è iperstatica lungo l' asse x,e che le reazioni vincolari Rua e Rub dovranno bilanciare il carico distribuito ovvero la loro somma dovrà essere uguale a q e che le reazioni verticali Rva e Rvb saranno uguali e opposte.

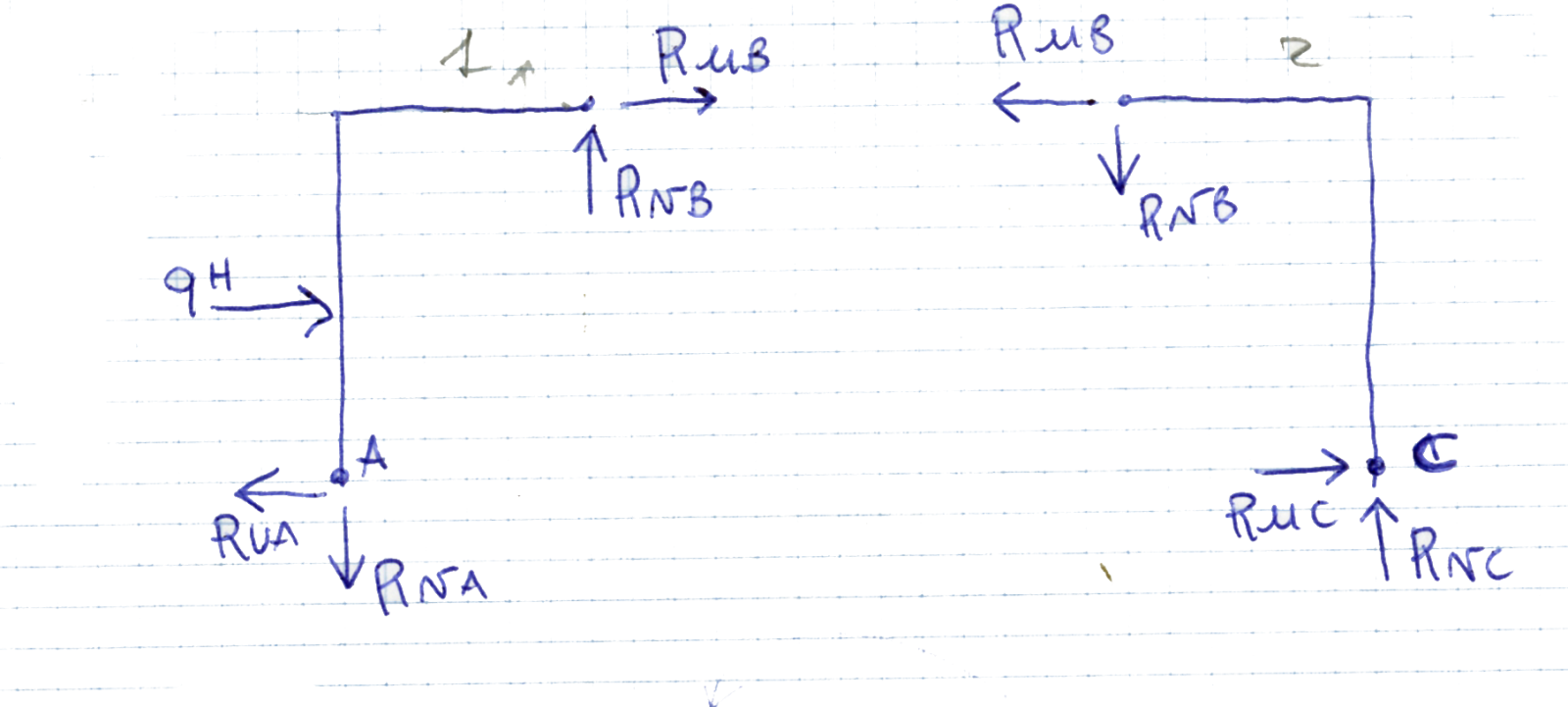
Per risolvere questa struttura dividiamola in due corpi, corpo 1 e corpo 2, ipotizzo il verso delle reazioni vincolari sia alle cerniere esterne sia a quella interna.

 

Reazioni vincolari nella cerniera interna B

Impongo il momento nel punto A e in B, ΣMA=0 e ΣMC=0 e li metto a sistema per trovarmi le reazioni vinvolari

ΣMA=0

-qh²/2-RuBh+ RvBl=0

ΣMC=0

RvBl+ RuBh=0 => RvB=- RuBh/l

Sostituisco il valore RvB dentro l' equilibrio alla rotazione in A, ΣMA=0 e ottengo RuB

-qh²/2-RuBh+ (-RuBh/l)l =>2 RuBh= -qh²/2 => RuB= -qh/4

Sostituisco il valore trovato di RuB= -qh/4 dentro RvB=- RuBh/l e trvo che RvB= qh²/4l

 

RuB= -qh/4

RvB= qh²/4l

 

Reazioni vincolari nella cerniera esterna A

u) qh+ RuB-RuA=0

Conoscendo RuB posso trovare RuA:

RuA= qh-qh/4

RuA=3/4 qh

 

v) RvA= RvB=qh²/4l                                                            

 

Reazioni vincolari nella cerniera esterna B

u) RuB=RuC= -qh/4

v) RvB= RvC=qh²/4l

 

Determino l' andamento di N(s), T(s) e M(s)

dN(s)/ds+ q1(s)=0

dT(s)/ds+ q2(s)=0

dM(s)/ds+ T(s)=0

 

 

 

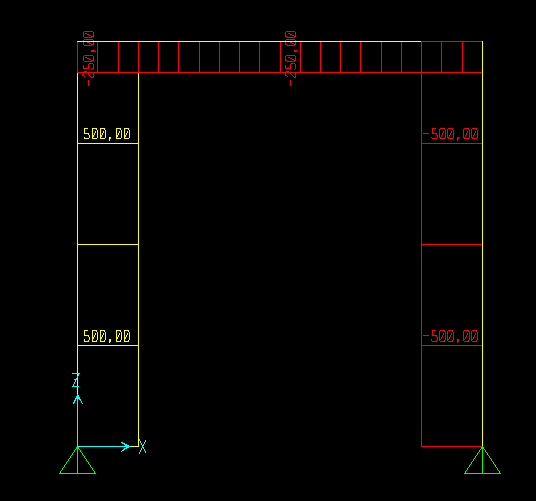
Una densità di carico distribuito q1 su x non è presente infatti il grafico dello sforzo assiale risulta costante

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

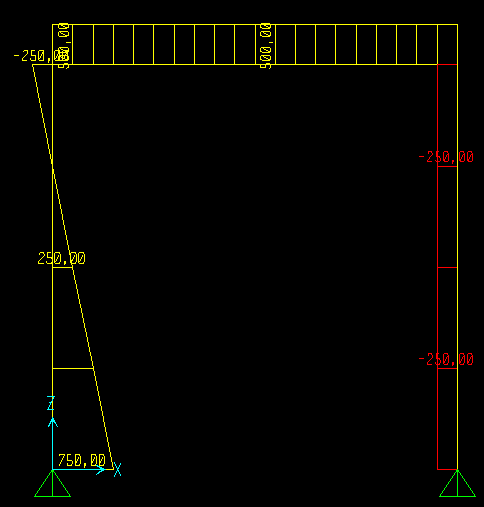
Una densità di carico distribuito q2 su y  è presente infatti il grafico dello sforzo di taglio risulta lineare lungo l' asta interessata dal carico distribuito con un diagramma a farfalla asimmetrica e risulta costante nelle due aste rimanenti in cui il carico distribuito nn è presente:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dM(s)/ds+ T(s)=0, da questa formula risulta che il diagramma del momento è la derivata del taglio per cui il taglio nel prima asta verticale con carico distribuito avendo un andamento lineare, il momento di conseguenza su quell' asta sarà parabolico, nelle altre due aste dove il diagramma del taglio era costante avremmo un momento lineare:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Esercitazione_Portale a 3 cerniere con carico carico concentrato lungo l' asse delle Y o Z

 

  

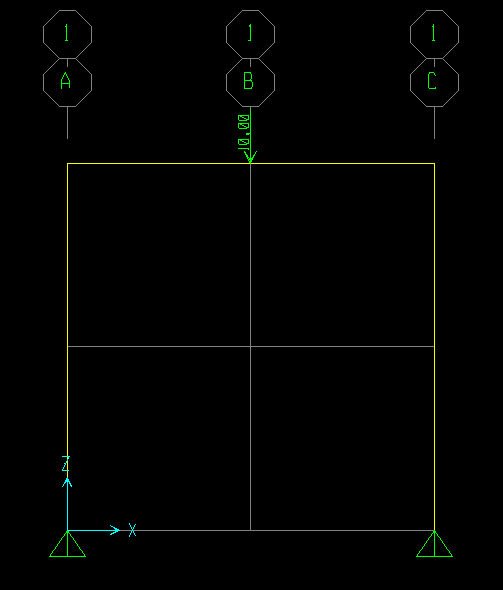
Dati

q= 100 kN/m                                             

h=10m

l=5m

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

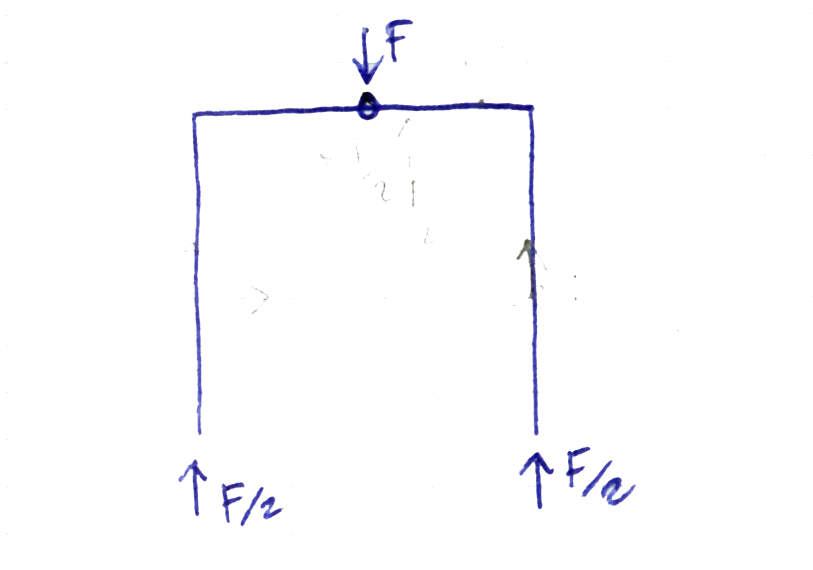
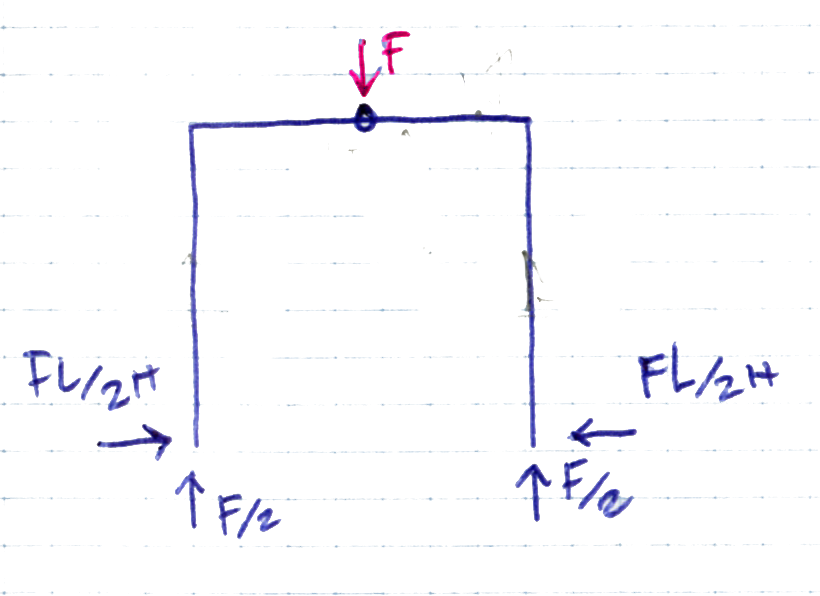
Possiamo vedere che la struttura è tutta simmetrica, tenendo il corpo unito, senza dividirlo, di primo acchitto notiamo subito un carico F centrale, in cerniera, in l/2. A tale forza F dovranno corrispondere 2 Reazione vincolari che saranno la somma di F con verso opposto a F, per cui avremmo F/2 e F/2.

Illustro il ragionamento riportato di sopra, dividendo la struttura e facendo vedere come le reazioni vincolari in direzione y siano uguali a F/2.

 

 

 

 

 

 

 

 

 

 

Divido il corpo in 3, isolando la cerniera, sommo i momenti del corpo 1 e 3 li impongo uguali a zero e opero all' interno dell' equazione una sostizione con ΣRv=0 della cerniera, per trovare una reazione vincolare verticale.

 

 

 

 

Reazioni vincolari nel corpo 1

ΣRu=0 => RuA=RuB

ΣRv=0 => RvA=RvB'

ΣMA=0 => RuB H- RvB' l=0

 

Reazioni vincolari nel corpo 2, cerniera

ΣRu=0 => RuB=RuB

ΣRv=0 => RvB'-RvB''-F=0

Con ΣRv=0 posso fare RvB'= RvB''+F

 

Reazioni vincolari nel corpo 3

ΣRu=0 => RuC=RuB

ΣRv=0 => RvB''=-RvC

ΣMC=0 => -RuB H- RvB'' l=0

 

SOMMO I MOMENTI DEL CORPO 1 E 3 E LI PONGO UGUALI A ZERO

RuB H- RvB' l -RuB H- RvB'' l=0 => - RvB' l - RvB'' l=0

Ora sostituisco l' equazione RvB'= RvB''+F dentro - RvB' l - RvB'' l=0

Ottengo che

RvB''= - F/2

Sostituendo il valore trovato di RvB" lo sostituisco dentro le ΣRv=0 dei relativi corpi 1-2 e 3

Dal corpo 2 ottengo RvB'= F/2

Dal corpo 1 Ottengo che Rva= F/2

Dal corpo 3 ottengo che Rvc= F/2

 

Trovate le reazioni vincolari lungo Y è facile trovarsi le reazioni vincolari lungo l' asse X, sostituendo i valori trovati dentro i momenti del corpo 1 e 3, avrò:

 

RuB= Fl/2H= RuA= RuC

C.V.D.

 

Determino l' andamento di N(s), T(s) e M(s)

 

Non avendo un carico distribuito le 3 equazioni differenziali non valgono più per studiarsi i 3 diagrammi.

dN(s)/ds+ q1(s)=0

dT(s)/ds+ q2(s)=0

dM(s)/ds+ T(s)=0

 

Infatti esistono le 3 EQUAZIONI DELLA SINGOLARITA'

Fx = Nnegativo o di sinistra - Npositivo o di destra

Fy= T negativo o di sinistra – T positivo o di destra

C= M negativo o di sinistra – M positivo o di destra

 

In questi casi dove la forza concetrata viene applicata, in quel punto ci sarà un salto nella sezione, ovvero un punto di non derivabilità e questo salto sarà pari alla forza concetrata.

Quindi se c è un salto nel taglio c' è anche un salto nella derivata del momento, ovvero un punto di spigolo che è un punto di non derivabilità.

 

 

 

 

 

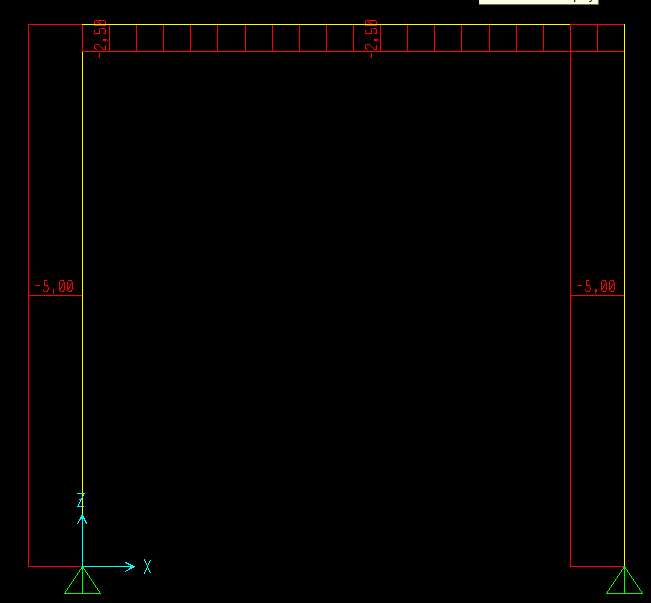
Il diagramma dello sforzo assiale è costante sia nelle 2 aste verticali sia nell' asta orizzontale ed è pari alle reazioni vincolari che stanno ai bordi.

 

 

 

 

 

 

 

 

 

 

 

 

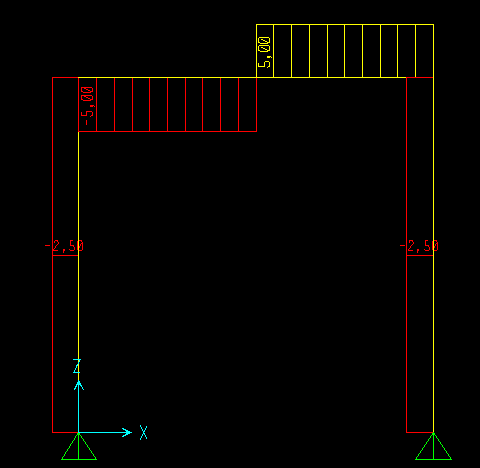
Il diagramma del taglio è costante nelle aste verticali ed è pari alle reazioni vincolari ai bordi.

Nell' asta orizzontale è costante con un salto pari alla fornza concetrata F nel punto in cui è applicata la forza.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

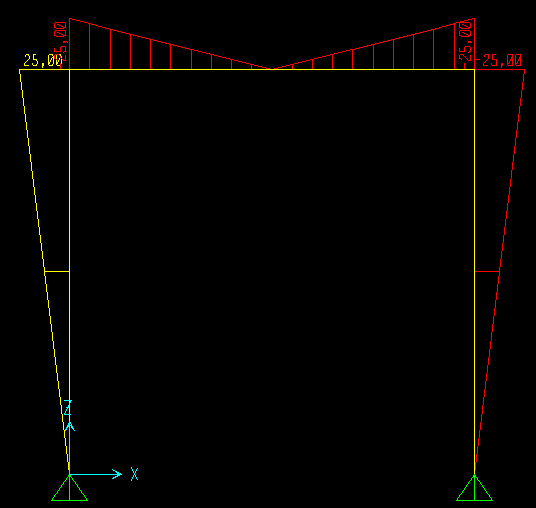
Il momento é lineare su tutte e 3 le aste, è zero nelle nelle 3 cerniere, raggiungendo agli spigoli della struttura un valore lineare (triangolare) pari a Fl/2.

 

 

 

 

 

 

 

 

 

Esercitazione_Portale a 3 cerniere con carico carico concentrato lungo l' asse delle X

 

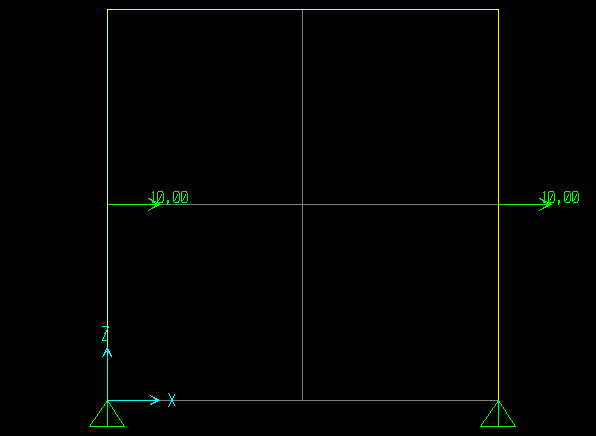
Dati

q= 100 kN/m

h=10m

l=5m

 

 

 

 

 

 

 

 

 

 

 

 

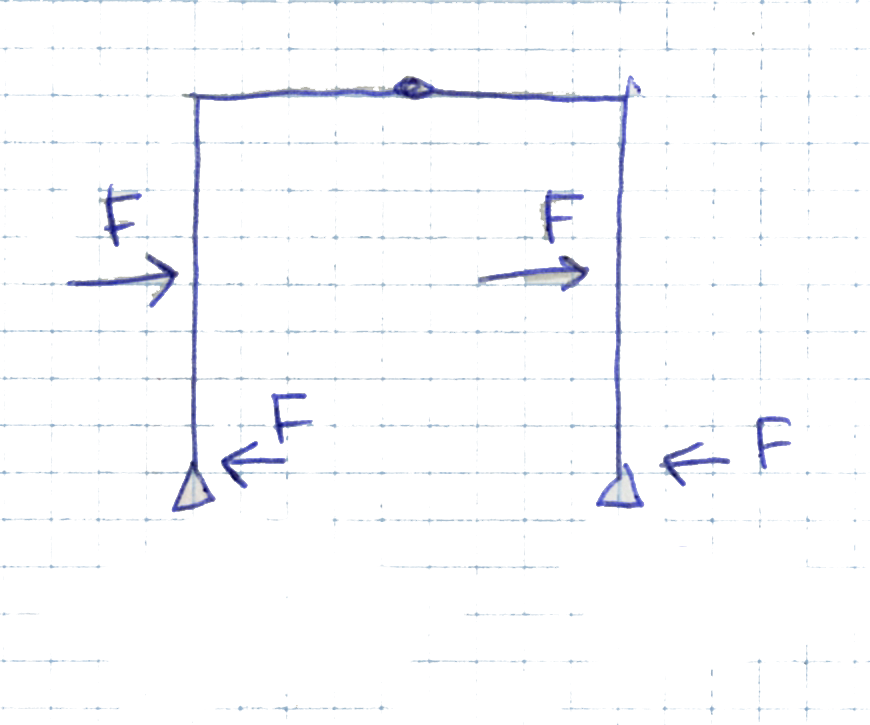
E' evidente che anche qui ci dovranno essere 2 reazioni vincolari con segno opposto a 2F con intensità pari a 2F, per far si che la strttura sia in equilibrio.

Condizione: iperstatica lungo l' asse X

 

 

 

 

 

 

 

 

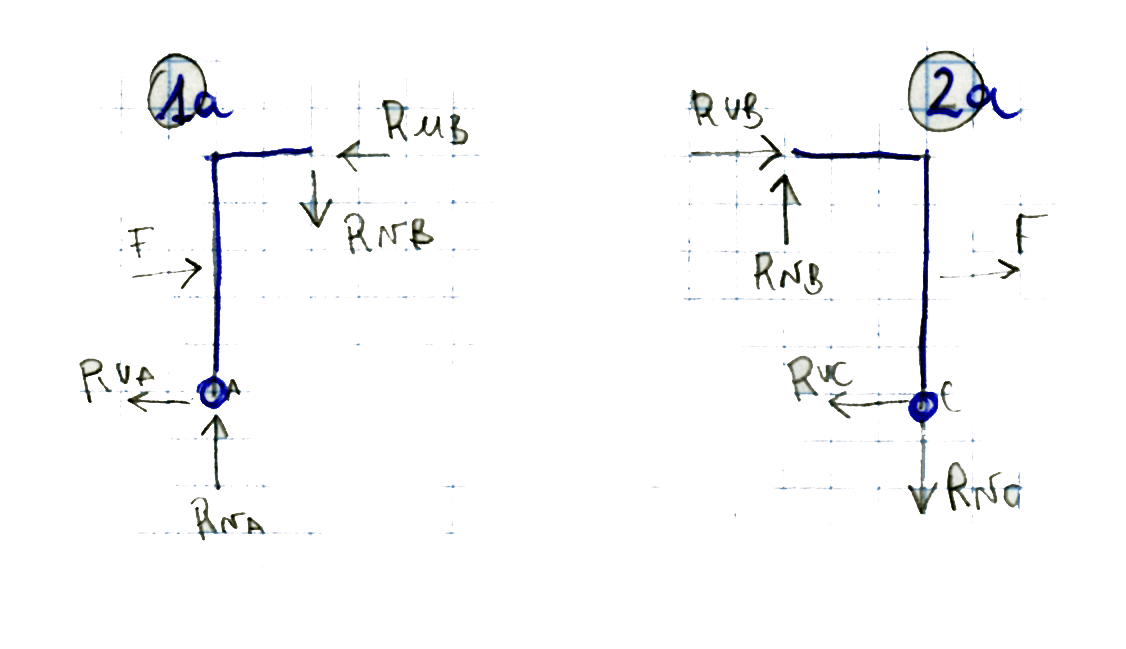
Stesso procedimento di prima:

Separo i due corpi, assegno ipotetiche reazioni vincolari, e faccio i momenti con polo nelle cerniere A e C per trovarmi le reazioni vincolari nel punto B (la cerniera interna).

 

 

 

 

 

 

Momento nel corpo 1

ΣRu=0 => - RuA+ F- RuB=0

ΣMA=0 => RuB H- RvB l – FH/2=0

 

Momento nel corpo 2

ΣRu=0 => RuB+ F- RuC=0

ΣMC=0 => -RuB H- RvB l – FH/2=0 => RvB l= -FH/2- RuBH <= sostituisco il valore dentro la prima equazione RuB H- RvB l – FH/2=0 e ottengo

RuB=0 <= sostituisco il valore dentro le equazioni della ΣRu=0 del corpo 1 e 2, e avrò:

RuA= F

RuC= F

La somma di RuC e RuA è proprio pari a 2F e riesce a bilanciare le due forze concetrate

C.V.D.

 

Per trovare le reazioni vincolari lungo l' asse Y o Z, basta inserire i valori trovati di RuB dentro:

RvB l= -FH/2- RuBH => RvB= - FH/2L= RvC

RuB H- RvB l – FH/2=0 => RvB= - FH/2L= RvA

 

 

 

 

 

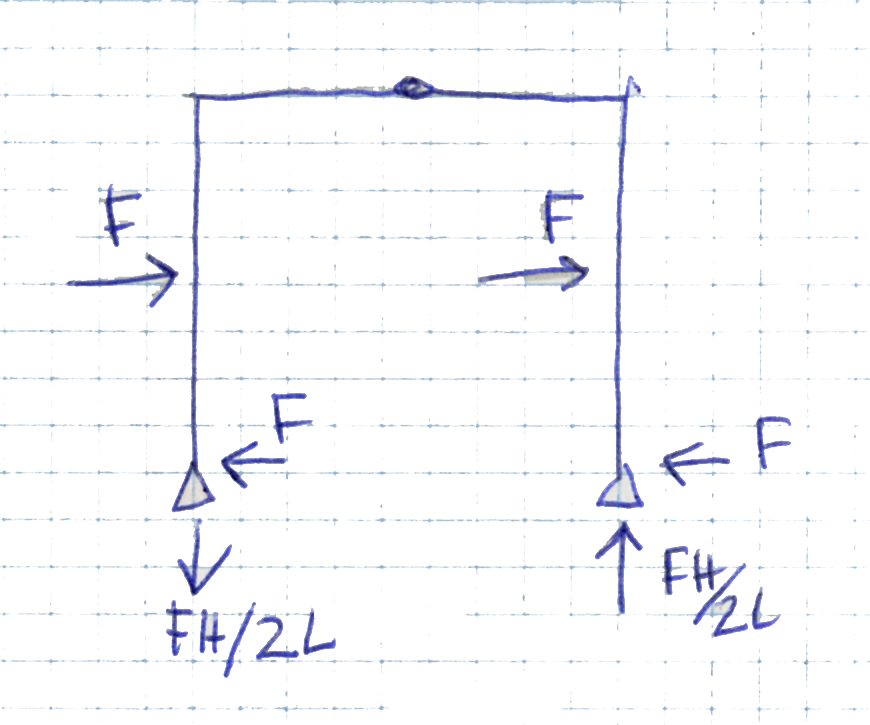
Il diagramma dello sforzo assiale è costante sia nelle 2 aste verticali ed è pari FH/2l

lo sforzo assiale è nullo nell' asta orizzontale.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

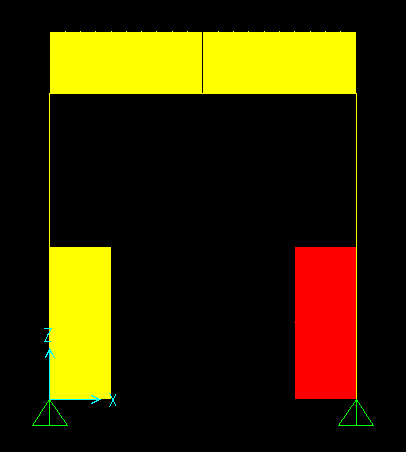
Il diagramma del taglio è costante fino a metà (c' è un salto nel diagramma dovuto alla forza concetrata) nelle aste verticali ed è pari a F

Nell' asta orizzontale è costante ed è pari a FH/2l

 

 

 

 

 

 

 

 

 

 

 

 

 

 

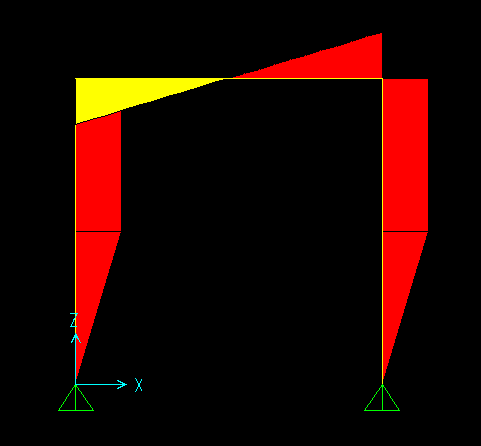
Il momento é lineare su tutte e 3 le aste, nelle aste verticale c' è un punto di spigolo (dove è presente la forza concentrata).

Nell' asta orizzontale il momento è lineare e a farfalla.

 

 

 

 

 

 

 

 

 

 

 

Esercitazione_ Dimensionamento travi e travetti in acciaio, legno e cls

 

Ho preso in esame l' impalcato della casa a schiera a Fiumicino del laboratorio di Progettazione1, ho stabilito il telaio della struttura, ho preso in considerazione il piano a quota + 3.00, ho analizzato la trave 2AB, studiandone i carichi del solaio e progettandola in legno, acciaio e cls. Ho verificato i valori con excell e sap.

  

 

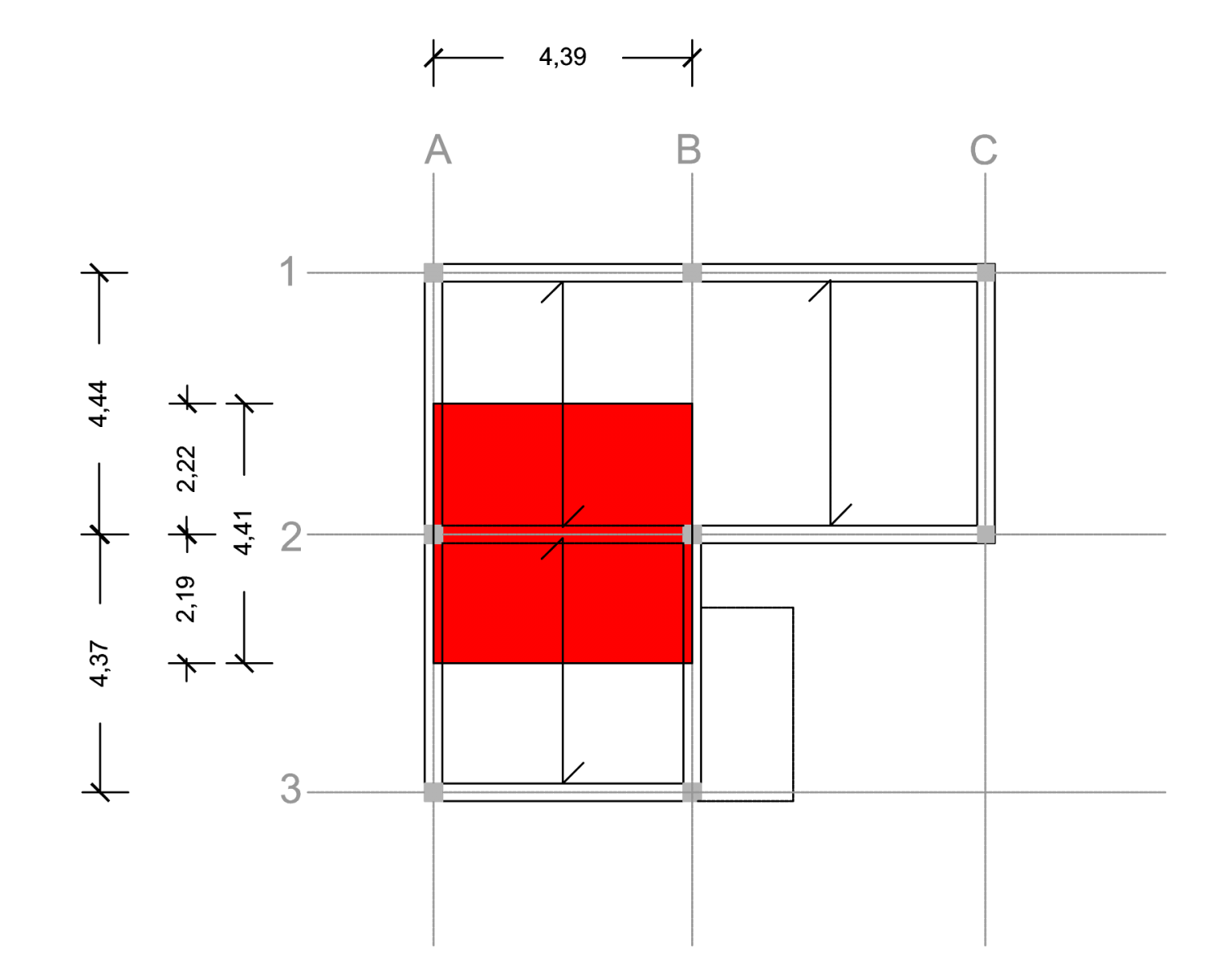
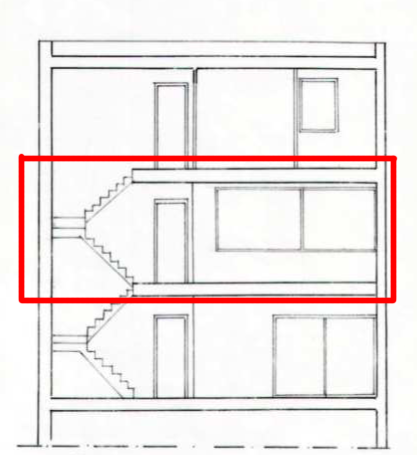
SOLAIO INTERPIANO_ Edificio di civile abitazione_ACCIAIO

 

 

1°PASSO_ Analisi dei carichi

 

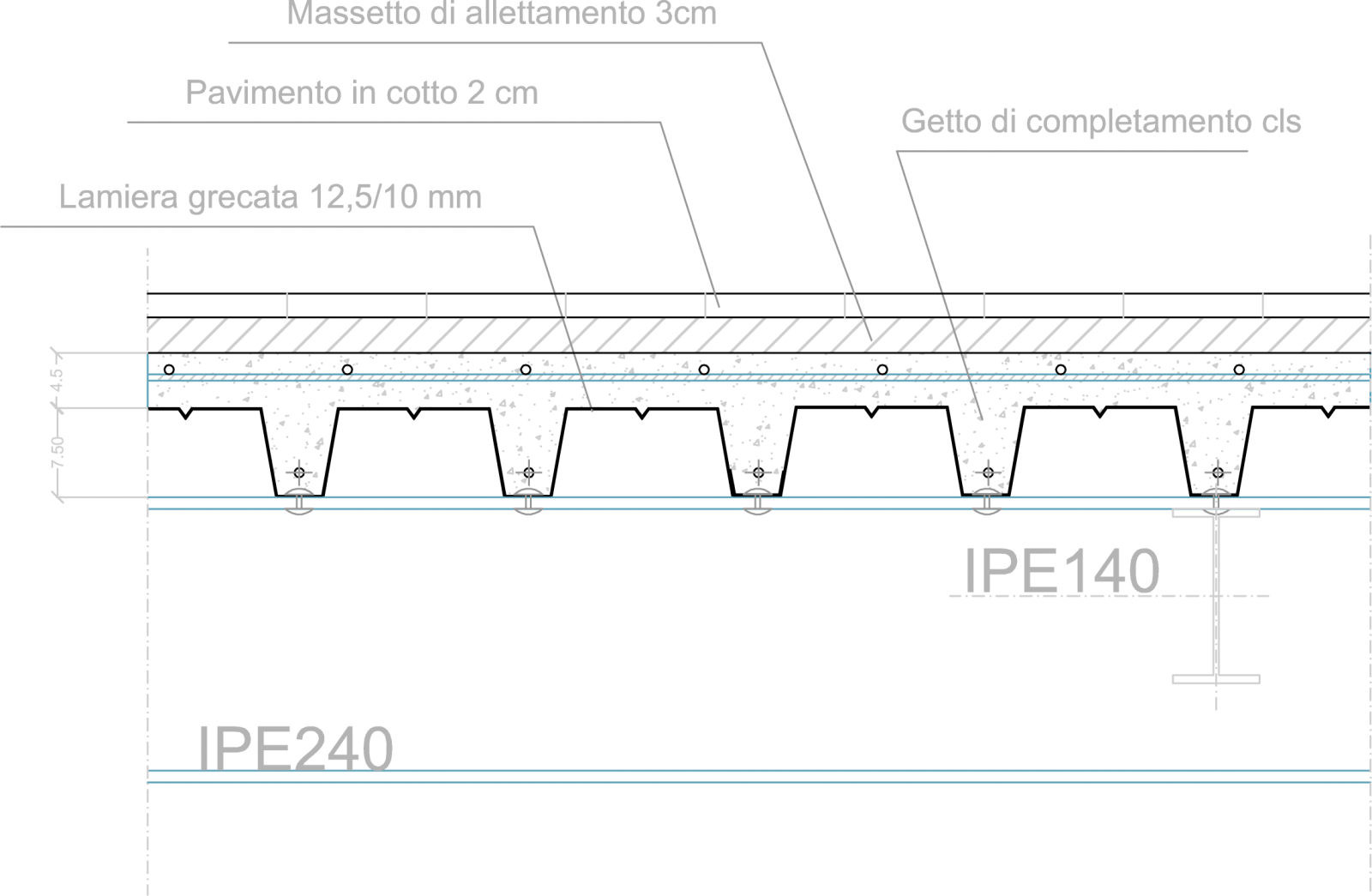
Carichi permanenti (Qp)

Il carico permanente è un peso che rimane per tutta la durata del tempo dell' edificio e varia solo nel caso vengano manomessi parte di questi elementi che vanno a comporre il carico.

 

Pavimento in cotto, peso specifico di 28kg/m² --->0,28kN/ m²

Massetto di allettamento 1800kg/m³ --->18kN/m³

Controsoffitto in pannelli di gesso rivestito per spessori standard di 12,5 mm, è di circa 10 - 12 kg/mq

Impianti 0.5kN/ m²

 

Carichi strutturali (Qs)

Getto di cls 2000kg/m³ ---> 20kN/m³

Lamiera grecata 7860kg/m³---> 79kN/m³

 

Tutti i materiali con il peso specifico espresso in Kg/m³ vanno moltiplicati per il loro spessore in modo tale che le lunghezze (kg/m³ e m) si semplicano per avere un' unità di misura di kg/m² e sommare tutti i carichi in base a questa uità di misura.

Massetto di allettamento_ 18x0.03= 0.54kN/m²

Getto di cls soletta _ 20x0.045= 0.9kN/m²

Getto di cls anima _ 20x0.075= 1,5kN/m²

Lamiera grecata _79x0.006= 0.5kN/m²

 

Carico accidentale (Qa)

I carichi accidentali sono pesi di cui non si riscontra costanza nell' arco della vita della struttura, in quanto, il loro valore cambia in base alla destinazione d' uso dell' edificio.

 

Il carico accidentale di un solaio di calpestio di civile abitazione è pari a 200kg/m²-->2kN/ m²

 

Determinazione del carico (q) sui travetti

Dati:

i= 1 m

L=4.45 m

Qa+Qp+Qs=6.32 kN/m²

Il carico (q) sulla trave sarà la somma di Qp, Qs e Qa moltiplicato per l interasse. Ottenendo così un carico a kN/m.

q= (Qa+Qp+Qs)x i---> (6,32)x 1=6,32 kN/m

 

 

2° PASSO_Progettazione del travicello

 

Il momento maggiore è pari a ql²/8= 15.85 kNm

Per dimensionare una sezione è bene usare sempre il momento maggiore in quanto quest'ultimo essendo legato a una caratteristica geometrica inerziale della struttura è utile al nostro scopo:

σ=Mmax/W

ma è anche vero che:

σ = f_D= fy_k/γ= M/W--------->W è la mia incognita in quanto ha intrinseche le caratteristiche geometriche della mia sezione in acciaio, per cui:

 

W> Mmax/f_D------>cerco il valore risultante sulle tabelle dei profili in acciaio e ne scelgo un valore maggiore al quale corrisponde una base e un altezza precisi del travetto

f_D= fy_k/γ= 275/1.05= 261.90 N/mm²

W> Mmax/f_D= 15.85 x 1000/ 261= 60.54

 

 

σ_Tensione

f_D_ Tensione di progetto

fy_K_ Tensione caratteristica, io ho scelto Fe 430 S275

γ_ coefficiente di sicurezza dato dalla normativa uguale a 1,05

 

A tale valore equivale un IPE 140:

W= 77.3 cm³,

P= 12,9 Kg/m => 0,129 kN/m² (ho trasoformato da Kg a kN e diviso per 1m, ovvero l interasse e ho ottenuto un unità di misura di kN/ m²)

 

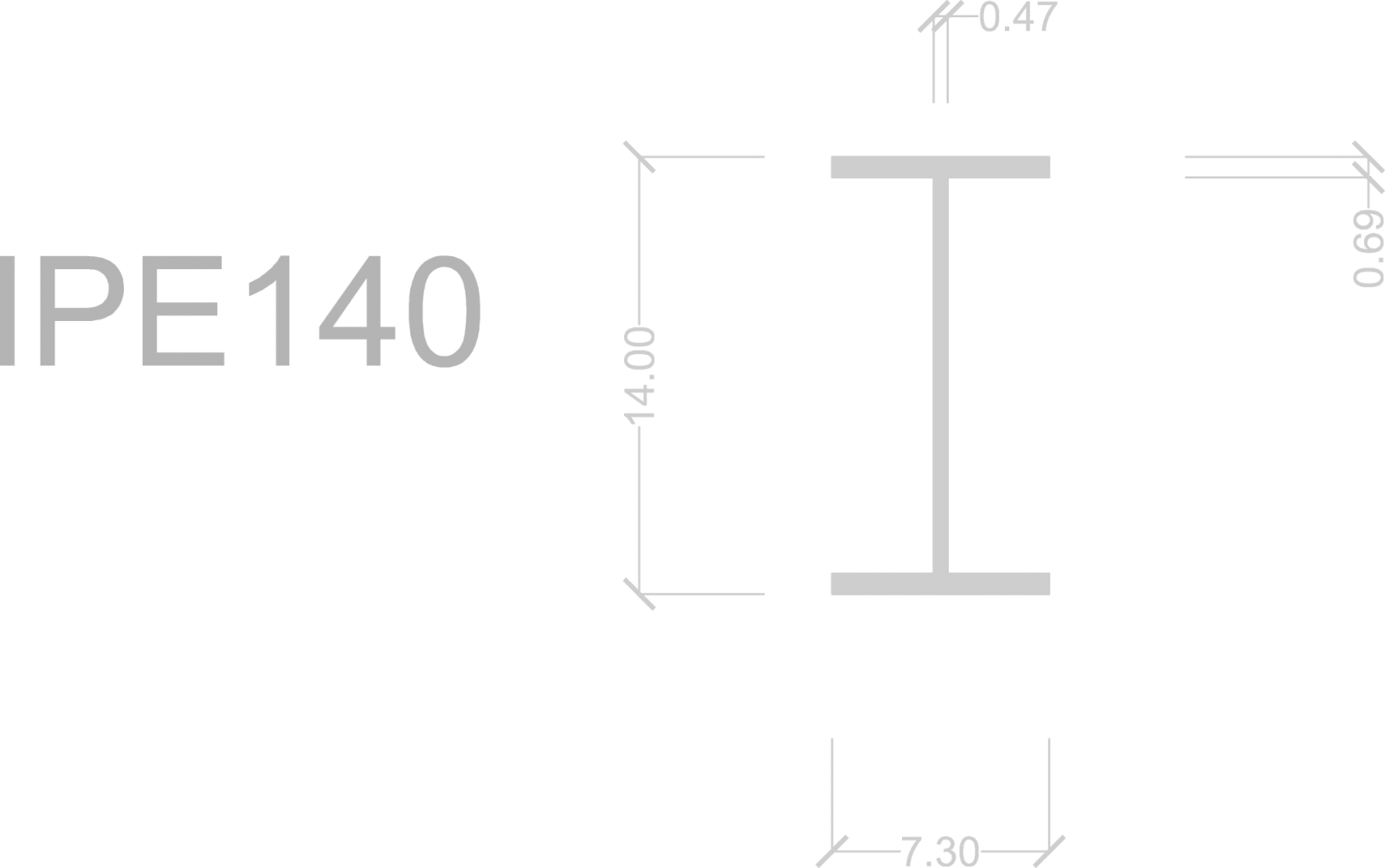
3° PASSO_ Progettazione trave principale

Dati:

i= 4.41m

L= 4.39m

Ptravicello= 0,129kN/m²

Per ottenere il carico totale sommo il carico precedente più Ptravicello e moltiplico per il nuovo interasse:

qtot= (6.32+0.129) x 4.9= 28.31kN/m

 

M= ql²/8= 68.20kNm

W> Mmax/f_D= 75.4 x 1000/ 261= 260 cmc

 

A tale valore equivale un IPE 240:

W= 324 cmc

 

 

 

 

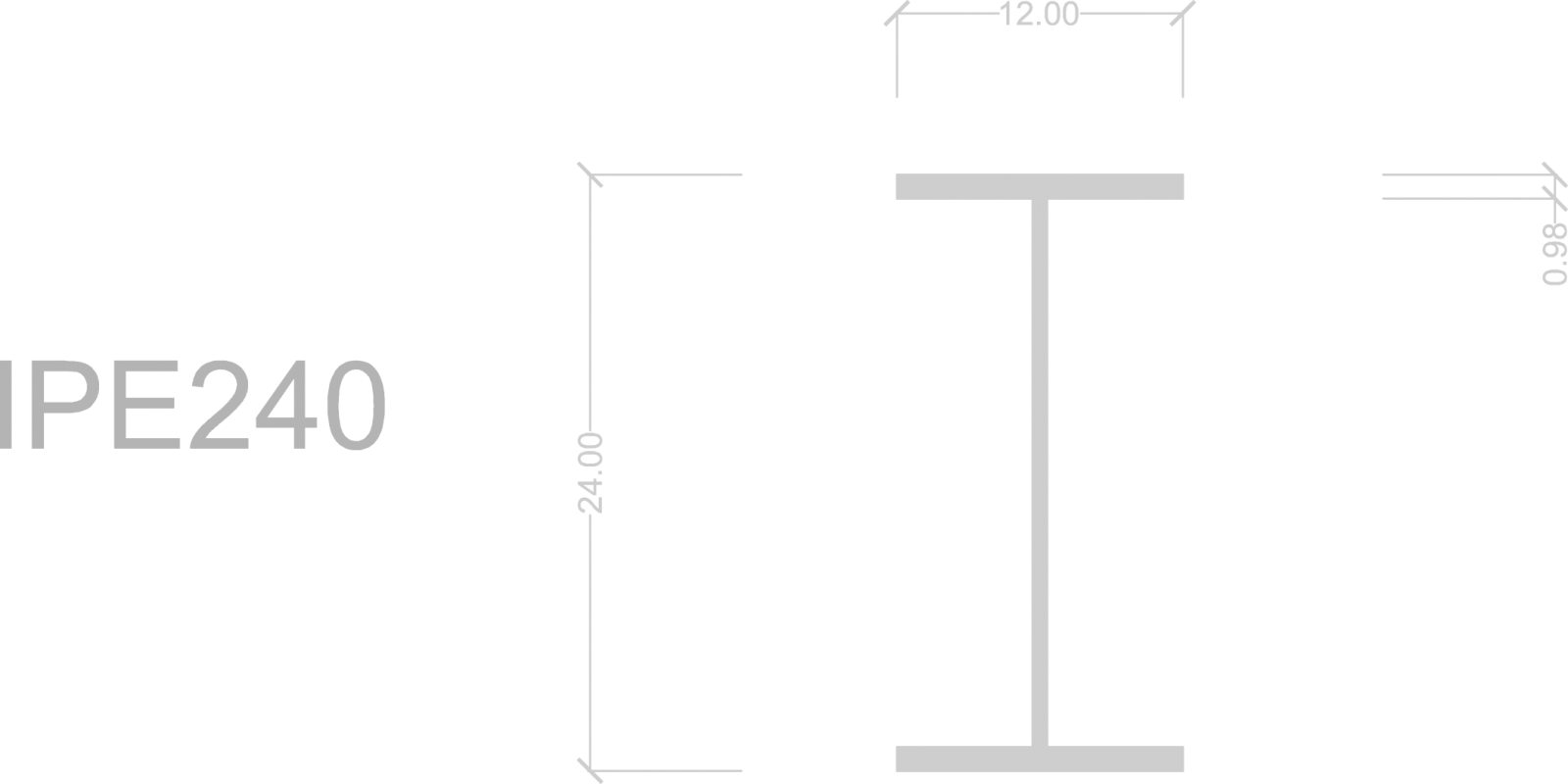
Verifica dei dati con il foglio elettronico per il calcolo dei travetti e della trave in acciaio

 

 

SOLAIO INTERPIANO_ Edificio di civile abitazione_LEGNO

 

 

 

1°PASSO_ Analisi dei carichi

 

Carichi permanenti (Qp)

Pavimento in cotto, peso specifico di 28kg/m² --->0,28kN/ m²

Allettamento 1800kg/m³ --->18kN/m³ x0.03= 0.54kN/m²

Massetto 2000kg/m³ ---> 20kN/m³x0.045= 0.9kN/m²

Impianti 0.5kN/ m²

 

Carichi strutturali (Qs)

Tavolato ligneo P= Volume x peso specifico= (1x1x0.025) x 6kN/m³= 0.15kN

Qs= 0.15 / 1m²= 0.15 kN/ m²

 

Carico Accidentale Qa

Il carico accidentale di un solaio di calpestio di civile abitazione è pari a 200kg/m²-->2kN/ m²

 

Determinazione del carico (q) sui travetti

Dati:

i=0.6m

L=4.45 m

Qa+Qp+Qs=4.37 kN/m²

Il carico (q) sulla trave sarà la somma di Qp, Qs e Qa moltiplicato per l interasse. Ottenendo così un carico a kN/m.

q= (Qa+Qp+Qs)x i---> (2,22+0.15+2)x 0.6=4.37 kN/m² x0.6m= 2.62kN/m

 

2° PASSO_Progettazione del travicello

 

Il momento maggiore è pari a ql²/8= 6.49 kNm, lo approssimo a 6.50 kNm

 

Ho scelto come classe di resistenza GL28h a cui corrisponde un:

fm_K= 28 N/mm² (immagine)

 

Kmod deve essere <1:

Kmod=0.5

 

f_D= Kmod x f_k/γ= 9.66 N/mm²

γ=1.45

 

Ho scelto la base del travicello pari a 10 posso ricavare

h=( 6 x M x 1000/b x σ)^ 0.5= 20.08cm approssimo a 25 cm

!!! σ= fm_K/ γ!!!!

 

Travicello_ b= 10cm e h= 25cm

 

3° PASSO_Progettazione della trave

 

 

Dati:

i= 4.41m

L= 4.39m

Qtravicello= A x peso specifico= 0.10 x 0.25 x 6= 0.15kN/m²

Per ottenere il carico totale sommo il carico precedente più Ptravicello e moltiplico per il nuovo interasse:

qtot= (4.37+0.15) x 4.41= 19,93 kN/m

 

Il momento maggiore è pari a ql²/8= 48.01kNm

 

Ho scelto come classe di resistenza GL28h a cui corrisponde un:

fm_K= 28 N/mm²

 

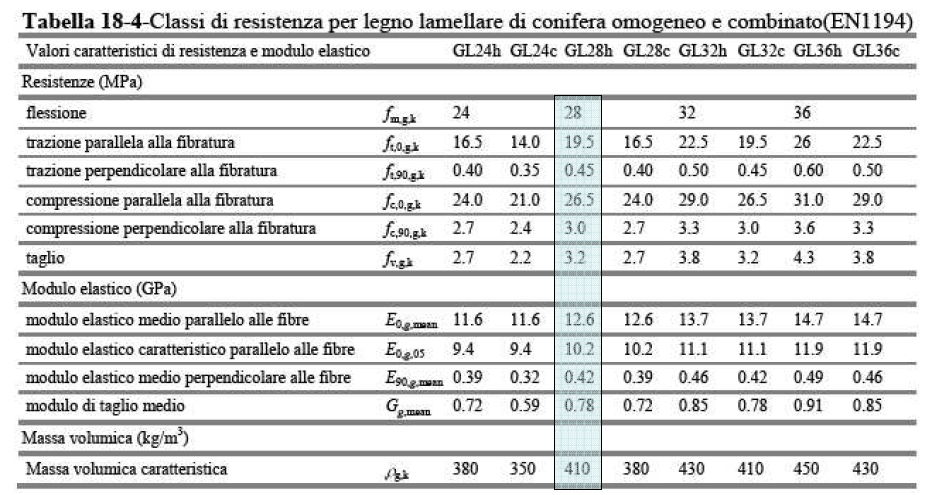
Kmod deve essere <1:

Kmod=0.5

 

f_D= Kmod x f_k/γ= 9.66 N/mm²

γ=1.45

 

Ho scelto la base della trave pari a 30 posso ricavare h=( 6 x M x 1000/b x σ)^ 0.5= 31 cm approssimo a 40cm

!!! σ= fm_K/ γ!!!!

 

Trave_ b= 30cm e h= 40cm

 

Verifica dei dati con il foglio elettronico per il calcolo dei travetti e della trave in legno

 

SOLAIO INTERPIANO_ Edificio di civile abitazione_C.A.

 

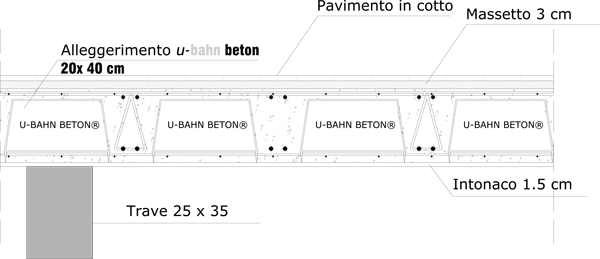
ALLEGGERIMENTO PER SOLAI MONODIREZIONALI IN C.A. GETTATI IN OPERA

U-Bahn Beton® è un cassero modulare in polipropilene riciclato appositamente progettato per la realizzazione di solai monodirezionali gettati in opera o semi-prefabbricati. I vari elementi, sovrapponibili nella porzione terminale, consentono lo sviluppo di travetti di qualsiasi lunghezza.Leggero e impilabile, risulta maneggevole nella posa in opera, razionale nell’utilizzo, non teme le intemperie ed è facile da stoccare in cantiere con minimi ingombri.Contrariamente a quanto avviene con le classiche pignatte in laterizio, il vuoto lasciato da U-Bahn Beton® potrà essere utilizzato per il passaggio di cavi e impianti.

 

 

1°PASSO_ Analisi dei carichi

 

Carichi permanenti (Qp)

Pavimento in cotto, peso specifico di 28kg/m² --->0,28kN/ m²

Massetto di allettamento 1800kg/m³ --->18kN/m³

Intonaco in gesso 1000 kg/ m³---> 10kN/m³

Impianti 0.5kN/ m²

 

Carichi strutturali (Qs)

Getto di cls 2000kg/m³ ---> 20kN/m³

Alleggerimento con U-Bahn Beton 1,40kg/m³---> 0.014kN/m³

 

Tutti i materiali con il peso specifico espresso in Kg/m³ vanno moltiplicati per il loro spessore in modo tale che le lunghezze (kg/m³ e m) si semplicano per avere un' unità di misura di kg/m² e sommare tutti i carichi in base a questa uità di misura.

Massetto di allettamento_ 18x0.03= 0.54kN/m²

Getto di cls soletta _ 20x0.040= 0.8kN/m²

Getto di cls anima _ 20x0.2= 4kN/m²

Intonaco _10 x 0.015= 0.15 kN/m²

U-Bahn Beton _0.014 x 0.01= 0.00014 kN/m²

Carico accidentale (Qa)

Il carico accidentale di un solaio di calpestio di civile abitazione è pari a 200kg/m²-->2kN/ m²

 

Determinazione del carico

Dati:

i= 4.41m

L= 4.39m

Qa+Qp+Qs=4.37 kN/m²

Il carico (q) sulla trave sarà la somma di Qp, Qs e Qa moltiplicato per l interasse. Ottenendo così un carico a kN/m.

q= (Qa+Qp+Qs)x i---> (2+1.47+4.80)x 4.41=36.47kN/m

 

 

2° PASSO_Progettazione trave

Momento massimo Agente

M= ql²/8= 87.85 kNm

Calcolo della tensione di progetto dell' acciaio

f_D= fy_k/ 1.15= 391.30 N/mm²

Classi e caratteristiche meccaniche dell' acciaio da cemento armato

In merito all'acciaio da cemento armato normale, o acciaio per armatura lenta, il Decreto Ministeriale 14 gennaio 2008, in vigore dal 1 luglio 2009 prevede l'utilizzo solo delle seguenti classi di acciaio nervato (ad aderenza migliorata):

• B 450 C (acciaio laminato a caldo):caratterizzato da una tensione di rottura non inferiore a 540 N/mm²; da una tensione di snervamento non inferiore a 450 N/mm² e da un allungamento totale a carico massimo non inferiore al 7%;

• B 450 A (acciaio trafilato a freddo):caratterizzato da una tensione di rottura non inferiore a 540 N/mm²; da una tensione di snervamento non inferiore a 450 N/mm² e da un allungamento totale a carico massimo non inferiore al 3% (minore duttilità rispetto al precedente).

La normativa prevede inoltre per l'acciaio B 450 A una tensione di progetto f_yd inferiore a quella dell'acciaio B 450 C infatti per quest'ultimo la tensione di snervamento f_yk viene divisa per il solo coefficiente parziale di sicurezza dell'acciaio γ_ms =1,15 secondo la formula:

• f_yd = f_yk/γ_ms

mentre il secondo anche per un ulteriore coefficiente di modello γ_e = 1,20 secondo la formula:

• f_yd = f_yk/(γ_ms*γ_e)

L'acciaio B 450 C è più duttile ed è l'unico ammesso in zona sismica.

 

Calcolo della tensione di progetto del calcestruzzo

f_D= fc_K/γ => 40/1.75= 22.86 N/mm²

fc_K= è la resistenza a compressione di una provino di forma cilindrica

γ = coefficiente di sicurezza

Altezza utile h

L' altezza utile trave è la distanza dell’armatura tesa dal lembo compresso.

Decido la base della sezione b= 25 cm per calcolarmi l' altezza utile

Determino con excell α= fd_c/ (fd_c+fd_s/15)= 0.47 (numero puro)

Determino con excell r= ( 2/( α ( 1- α/3)))^0.5= 2.25 (numero puro)

Sono tutti valori utili per trovare l' altezza utile in fatti:

h=r√(M/ fD_c x b) = 27,93 cm

Altezza minima H

L' altezza minima della sezione in c.a. Data da

H= h+ c= 32,95 => 35cm

c= copriferro pari a 5 cm

Normalmente si usa il termine di copriferro sia per indicare la quantità di calcestruzzo che ricopre le armature sia la distanza tra il bordo teso della sezione e il baricentro delle armature resistenti nel calcolo delle sezioni in cemento armato.

b=25cm

H= 35 cm

Verifica del dimensionamento

Per verificare che il dimensionamento appena fatto sia giusto aggiungo al carico strutturale il peso della mia trave e mi ricalcolo l' altezza.

qtrave= A x 2500/ 100= (0.25 x 0. 35) x 25= 2.18 kN/m

Per rendere kN/m in kN/m² devo dividere qtrave per l interasse e ottengo

qtrave= 2.18/ 4.41= 0.49 kN/m²

Lo aggiungo al carico strutturale ottengo un H= 33.74

La mia trave b=25 e H=35 è verificata

 

ESERCITAZIONE_STRUTTURE RETICOLARI SPAZIALI

Padiglione a Segrate Milano

Introduzione

Le strutture reticolari spaziali sono di solito utilizzate per soluzioni multi direzionale permettendo di realizzare lunghe campate (i.e. luci ampie) per mezzo di un numero limitato di supporti. Traggono la loro forza dalla rigidità intrinseca del telaio triangolare; le flessioni ai carichi (i.e. momenti flettenti) sono trasmesse come tensione e carichi di compressione lungo la lunghezza di ogni puntone.

La loro geometria è spesso basata su solidi platonici. La forma più semplice è una lastra orizzontale di piramidi a base quadrata interconnesse fra loro e costruite per mezzo di montanti in alluminio o acciaio tubolare oppure moduli di base cubica.

Storia

Le strutture reticolari furono sviluppate indipendentemente da Alexander Graham Bell intorno al 1900 e Buckminster Fuller nel 1950. L'interesse di Bell fu primariamente concentrato sulla progettazione di telai rigidi per l'ingegneria nautica ed aeronautica. Gli interessi di Buckminster Fuller furono invece le strutture architettoniche sulle quali queste ebbero un'influenza più duratura. Le strutture reticolari spaziali sono una tecnica ormai largamente diffusa nell’architettura e nell’edilizia con particolare riguardo alla realizzazione di ogni tipo di struttura con grandi campate e leggerezza complessiva (e.g. edifici commerciali e industriali, copertura di aree archeologiche, spazi universitari, torri porta insegna, torri di illuminazione).

 

RETICOLARE SPAZIALE SCHEMA CUBICO

Lo schema cubico risulta composto da due piani di coordinazione a maglie regolari con i nodi allineati in verticale. In tal modo si ottiene una composizione regolare di celle cubiche che devono essere completate da tutte le diagonali di ciascun parallelogramma presente nella struttura. La cellula cubica si presta bene ad impostare strutture di tipo lineari quali travi, torri e portali.

 

Da Autocad a Sap

1°step_

_ Impostiamo le unità di misura da FORMATO=>unità di misura=> metri

_ Creare un nuovo layer chiamato "aste" per riportarlo in sap

 

Questa è la strttura reticolare spaziale che dobbiamo fare:

 

Ora riporterò gli step di questo processo progettuale, inziato da autocad.

2° step_ Processo progettuale

1_Disegno in pianta in 2D il mio modulo di partenza quadrato di lato 2m x 2m, utilizzo la spline e come riferimento iniziale di coordinate per il mio disegno assegno nella riga dei comandi 0,0,0.

DisegnO però un profilo a C (per evitare la sovrapposizione dell' asta ogni volta che si usa il comando SERIE) e la diagonale del nostro quadrato aperto.

 

 

2_ Impostiamo la modalità 3D tenendo premuto la rotellina del mouse+ shift, selezioniamo l' oggetto, e sulla riga dei comandi scriviamo RUOTA3D,immettendo nella riga dei comandi l' angolo di 90° per ruotare l' oggeto sul piano XZ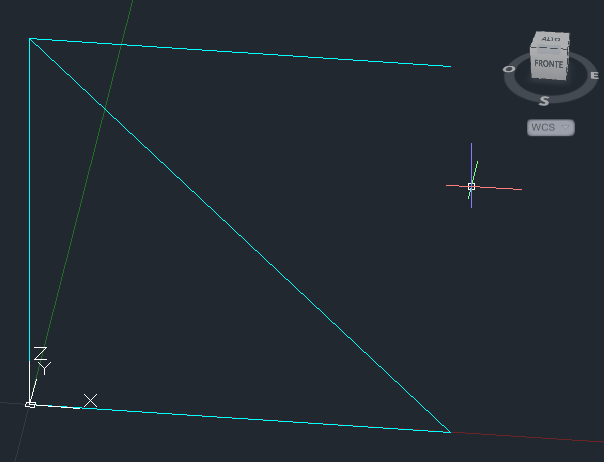

 

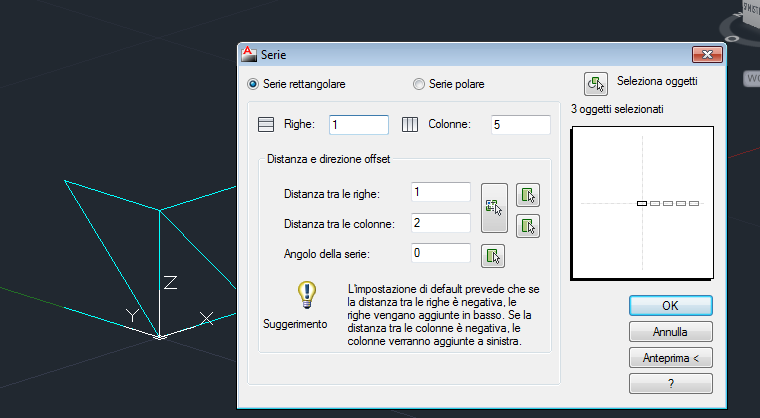
3_ Ora selezioniamo l' oggetto e digitiamo il comando "SERIE",

selezioniamo serie rettangolare

Righe 1 e colonne 4

Distanza tra le righe 1

Distanza tra le colonne 2 (ovvero la misura del nostro modulo di base)

 

Otteniamo questo:

 

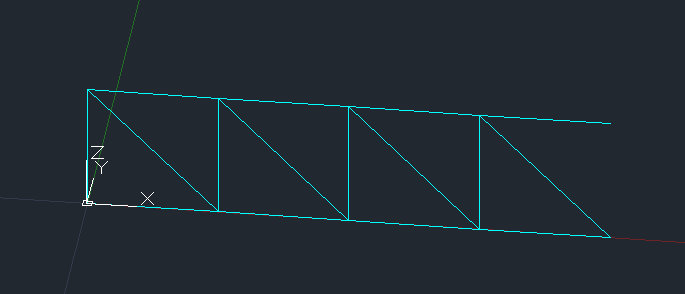
4_Ora disegnamo lungo l' asse y e quindi nel piano YZ l' asta superiore, inferiore e la diagonale, così:

 

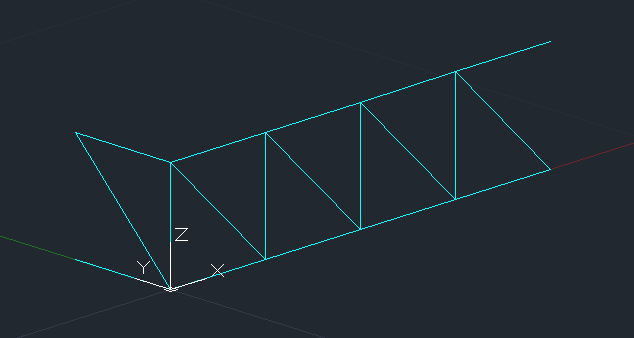
5_ Seleziono le due aste e la diagonale disegnate sopra,creando una serie sempre lungo l' asse X, con la differenza che il numero delle colonne questa volta è 5,

!!ovvero il numero delle aste della prima faccia lungo l' asse XZ. Ottengo questo:

 

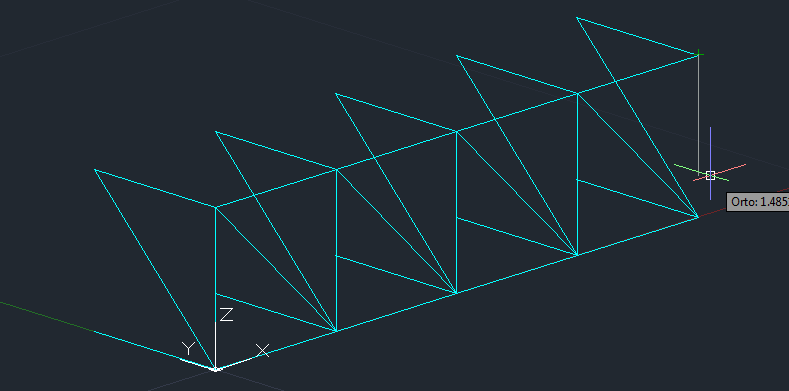
!!!!Tutto questo è possibile farlo fino ad ora senza cambiare l' UCS perchè si può usare la polilinea 3D oppure usando la semplice linea si usano gli SNAP ad oggetto in modo tale che i punti della linea/polilinea 3d finiscano in un punto a casa dello spazio 3d di autocad.!!!!!                                     

 

6_I piani su cui andremo a disegnare sono XY a quota Z=2 e XY a quota Z=0 in cui disegnamo l' asta obliqua...

 

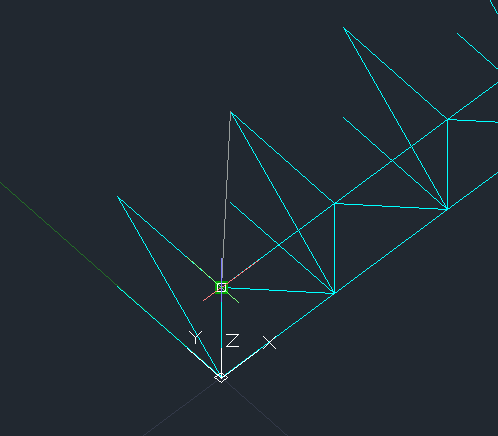
7_ Seleziono le due aste oblique e faccio SERIE lungo l' asse X con colonne 4,

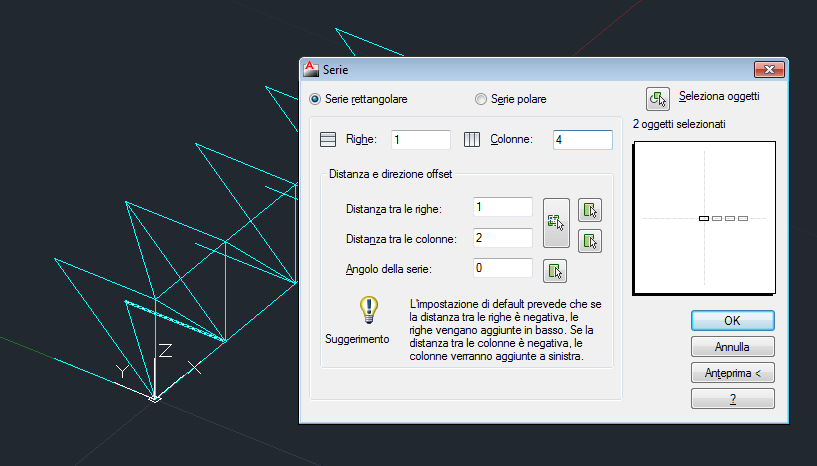
questo è il risultato:

 

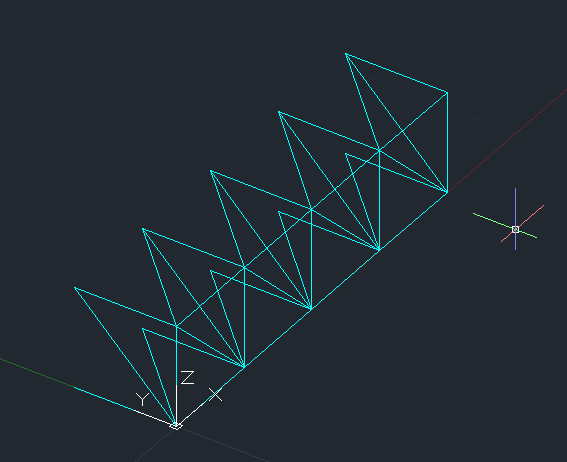
Questo qui sopra è il modulo 3d di base da cui partiremo per creare la piastra reticolare spaziale.

 

8_ Seleziono tutto, digito SERIE e sempre senza cambiare l' UCS,

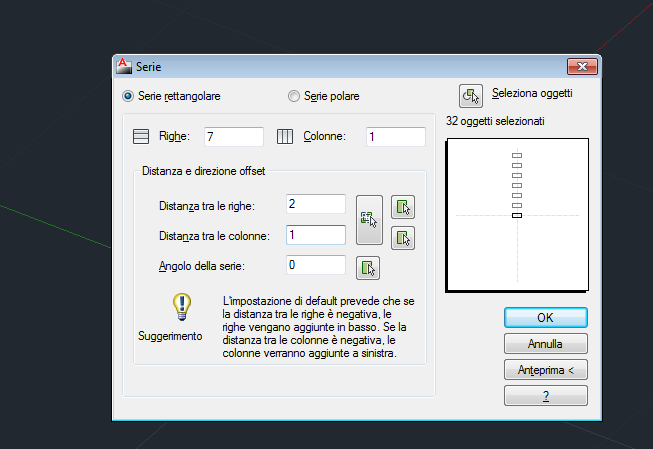
nelle righe inserisco 7,

nelle colonne inserisco 1,

distanza tra le righe 2,

distanza tra le colonne 1

E ottengo la serie del mio modulo di base lungo l' asse Y, piano YZ

 

 

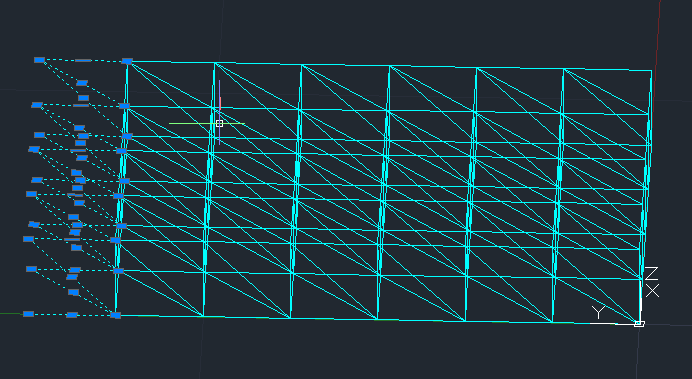
9_ Ora l' ultima campata rimasta aperta (la campata numero 7) è quella da eliminare, per ottenere una maglia di moduli cubici di 4x6. Questo è il risultato come nell' immagine iniziale:

 

Per evitare noie su SAP è bene selezionare tutto e digitare ESPLODI.

Andiamo su FILE-SALVA CON NOME e salviamo il file su DXF di AUTOCAD 2000

 

3° Step_ Processo progettuale su SAP

1_Come importare il file DXF su SAp

File=>import=> Autocad DXF file

Premete OK alla prima finestra di Import Information, alla seconda finestra DXF IMPORT, nel menu a tendina FRAME selezionate il layer ASTE creato in autocad

 

 

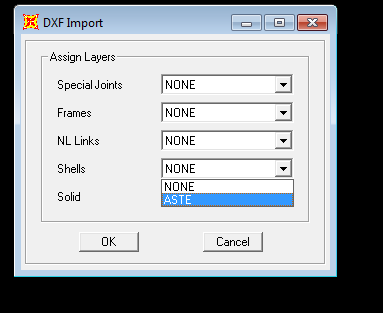
2_ Il file è importato correttamente!!

Selezioniamo gli appoggi ai quattro lati della struttura, andiamo su ASSIGN=>joint=>restraints e mettiamo le cerniere

 

 

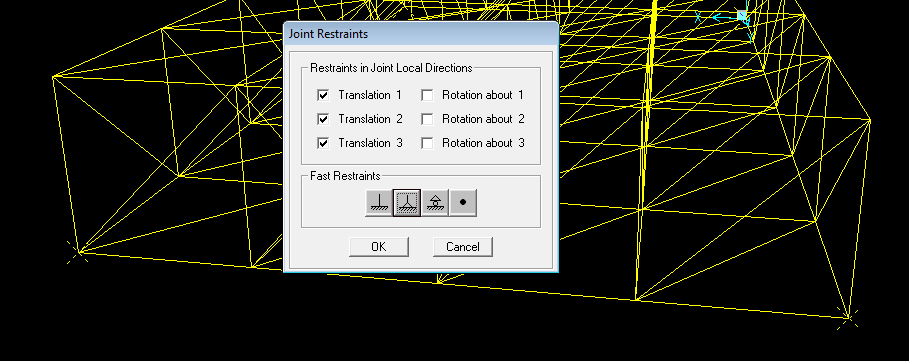
3_ Seleziono tutte le aste a cui rilascio il momento sia in 2.2 che in 3.3 (ASSIGN=> frame => release/... e selezioni i 2 momenti sopracitati).

4_ Definisco su LOAD PATTERN un carico distribuito,

5_ Define=> material e scelgo l' acciaio, sempre in define vado su section properties e scelgo una sezione tubolare in acciaio.

6_ Seleziono tutta la strttura vado su ASSIGN=>frame=>frame section e scelgo il materiale e la sezione che ho definito nel passo 5.

7_Seleziono solo i nodi superiore della struttura e assegno su FRAM LOADS=>distributed un carico pari a 40kN gravitazionale.

 

Fatto questo avvio l' analisi e ottengo la deformata, posso vedere il numero delle aste e posso vedere lo sforzo assiale di tutte le aste, utile a progettare l' asta compressa e tesa più sollecitata.

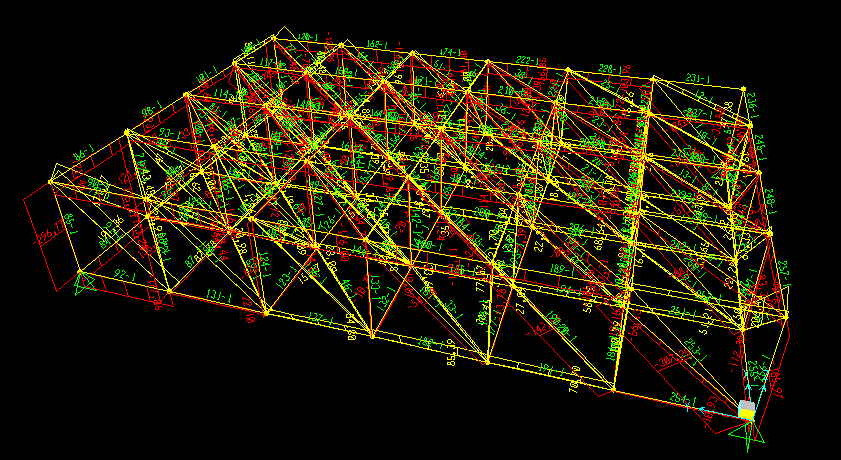
!!!!Questa strttura non è simmetrica perchè ha la lunghezza e la larghezza diverse!!

 

Conclusa la fase di analisi SAP ti permette di aprire una tabella con tutti i valore dello sforzo assiale di ogni singola asta e ti permette di esportala in EXCELL.

I valori negativi sono relativi all' asta compressa e i valori positivi sono relativi all' asta tesa, di questi valori per progettare l' asta della reticolare spaziale dobbiamo prendere gli soforzi assiali più grandi.

 

PROGETTO DELL' ASTA TESA

 

Asta numero 258 Nd= 258,93 kN

Questa è la tabella che SAP fornisce

 

Per trovarci la sezione del tubolare uso questa formula, σ=N/A, da cui poi mi ricaverò A che è la mia incognita

 

Sapendo che σ è anche uguale a fy_K/γ avrò fy_K/γ= N/A

 

Tiro fuori dall' equazione A che è la mia incognita:

A= N γ/ fy_K

Ho scelto un acciaio con S275=fy_K

γ= coefficiente 1,05

 

Mi sono cotruita una tabella in EXCELL per i calcoli.

 

Dal profilario ho scelto una sezione circolare che abbia un area maggiore di 9,89 cmq

Perfetto!! Scegliendo un area di 10,70 cmq Nd= 258,93 kn risulta minore di Ntrazione= 280, 23 kN

 

 PROGETTO DELL' ASTA COMPRESSA

Un elemento teso sopporta senza problemi una forza pari quasi a detto limite ( A⋅σ ), una membratura compressa può inflettersi e collassare sotto carichi sensibilmente inferiori, tanto

più piccoli quanto più la lunghezza è elevata nei confronti delle dimensioni della sezione.

Questo è un esempio dell’ampia e diversificata categoria di fenomeni complessivamente classificati come di instabilità.

Si parla di equilibrio stabile se il sistema a seguito di un disturbo piccolo a piacere si mantiene in un intorno altrettanto piccolo a piacere.

Si parla di equilibrio instabile se il sistema si allontana in modo incontrollabile con l’entità del disturbo.

Le aste compresse hanno appunto problemi relativi all' instabilità se sono sollecitate da un carico di punta.

Per questo motivo bisogna verificare a 1)resistenza a 2)stabilità e a 3)snellezza

 

Asta numero 253 Nd= 307,25

 

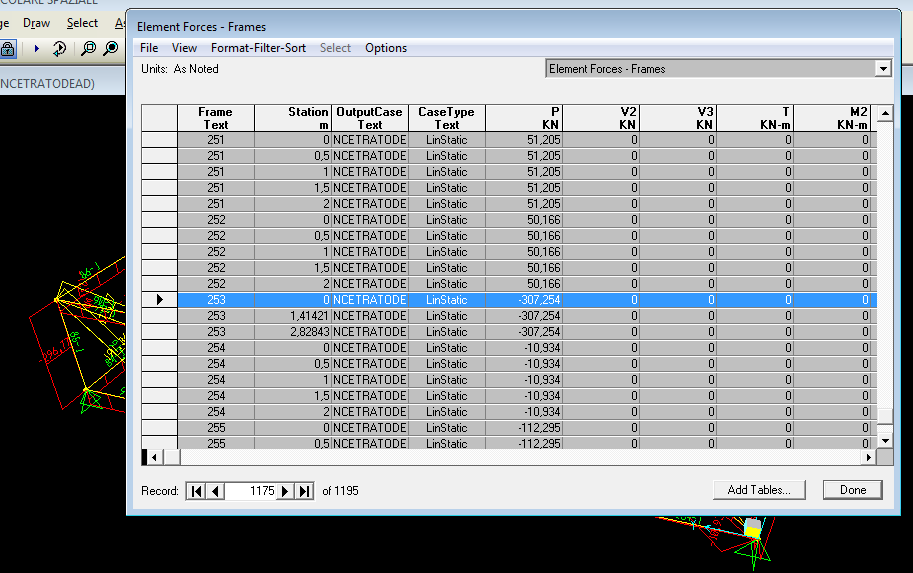
1)Nd< Ncres= A fy_K/γ

σ=N/A => fy_K/γ= N/A=> A= N γ/ fy_K

Tabella di Excell:

 

L' area minima è di 11, 73 cmq

sui profilari troviamo un area maggiore pari a 12, 50 cmq, con un giratore di inerzia di 3,92 cm utile a calcolarci la verifica a snellezza.

Verifco a resistenza i valori trovati Nd< Ncres= A fy_K/γ=327 kN è verificato in quanto è un valore maggiore della Nd di progetto

 

3)λ<200 => λ=lo/ρ <200

lo= βl

Dati:

β= è il coefficiente di libera inflessione e vale 1

lo=luce di libera inflessione

l=luce dell asta pari a 2,82

ρ= 3,92 cm

 

Devo verificare che λ<200 con i dati soprascritti e con il ρ= 3,92 cm che ho ricavato dalla verifica a resistenza nel passo 1), ecco i risultati con excell:

Il risultato è che λ= 71,94 che è un valore minore di quello imposto dalla normativa ovvero minore di 200, la verifica a snellezza è ok!!

 

!!!In fase di progetto posso ricavarmi ρ come dato di progetto da ricercare sulle tabelle dei profilari e ottengo tutti i dati relativi al tubolare in acciaio partendo dal giratore di inerzia in questo modo: ρ> βl/200

 

 

2)La verifica di stabilità di un' asta si effettua nell' ipotesi che la sezione trasversale sia uniformemente compressa. Quindi:

 

Nd< Nbrd

 

Nd=sforzo assiale di progetto preso dalla tabella di sap

Nbrd= è la resistenza all' instabilità dell' asta compressa

 

 

in cui Nbrd= χA fy_k/ γ

χ= 1/Ф + √ Ф² - λ'²< 1

χ è un coefficiente riduttivo di progetto

 

i due valori si trovano nel seguente modo:

Ф= 0,5 ( 1 + α ( λ' – 0,2) + λ'²)

α= è un valore tabellato preso da questa tabella in basso:

 

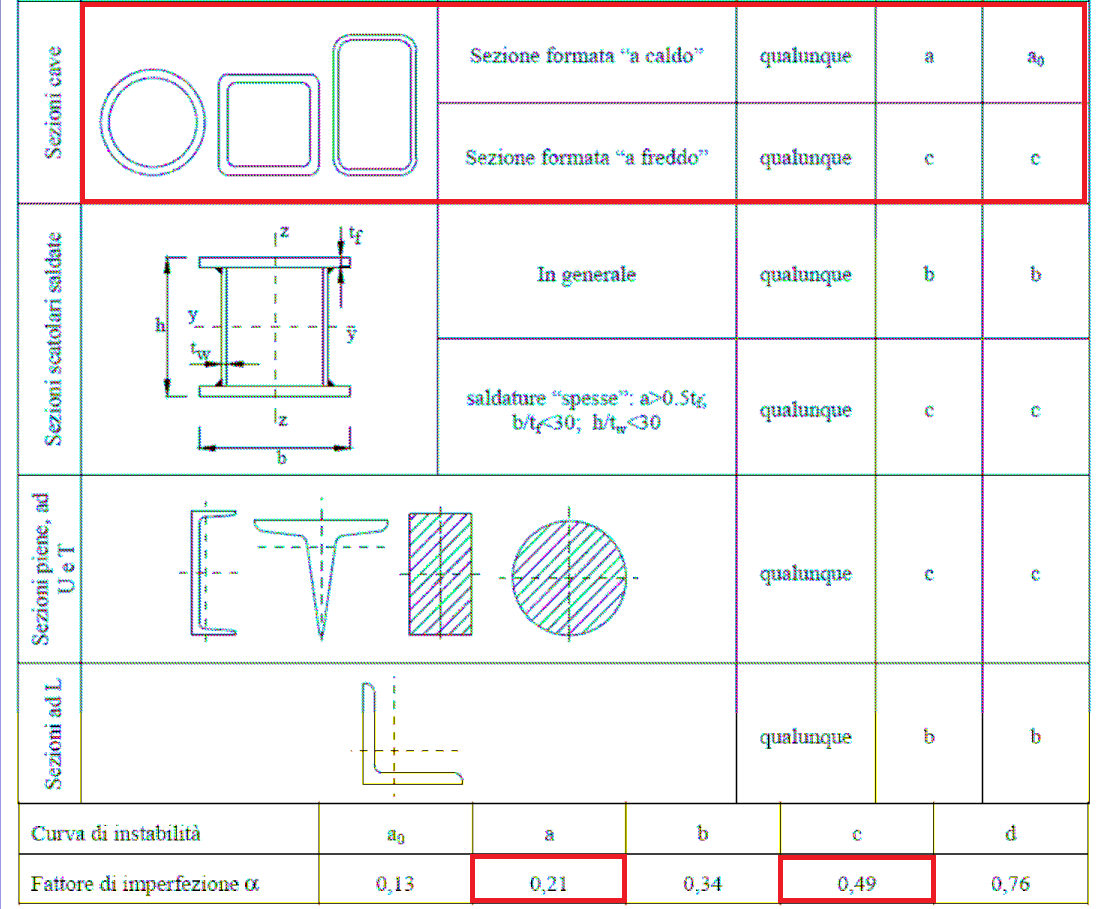
Scelgo il minore fra i due

 

λ'= √ A fy_K/ Ncr

Ncr= carico critico euleriano= π² E I/ lo²

Dati:

E= 210 000 Mpa

I(momento d' inerzia)= 192 cm alla quarta

lo=luce di libera inflessione 2,82 cm

α= 0,21

 

a)Ncr=π² E I/ lo²= 9,85 x 210 000 x 19200/79524= 499 411 N

 

Inserico Ncr dentro:

b)λ'= √ A fy_K/ Ncr= √ 1250 x 275/ 499 411= √0,68 = 0,82

Lambda soprassegnato è un valore adimensionale

 

Inserisco λ':

Ф= 0,5 ( 1 + α ( λ' – 0,2) + λ'²)= 0,5 ( 1 + 0,21 ( 0,82 – 0,2) + 0,68)= 0,9

 

Ora che ho finalmente  ho trovato Ф e λ' posso calcolarmi:

χ= 1/Ф + √ Ф² - λ'² = 1/ 0,9 +√ 0,82- 0,68 = 0,78

 

Verifico che con questi valori Nd sia minore di Nbrd

Nbrd= χA fy_k/ γ= 255,35 kN non è verificato

 

In questo caso la sezione circolare con Area di 12,50 cm² non è idonea alla resistenza a stabilità con un acciaio S275, per cui dovrò utilizzare una sezione circolare con un' area maggiore!!! Riprendo il profilario

   

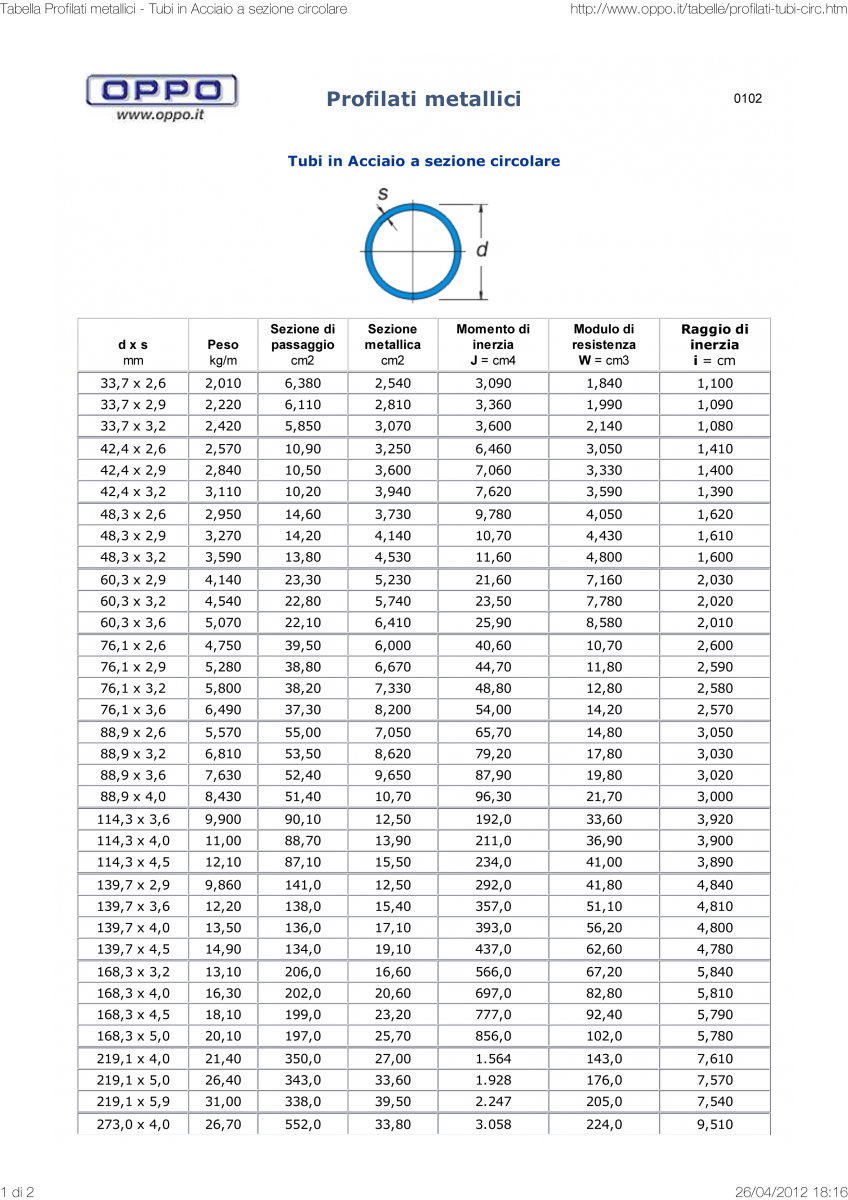
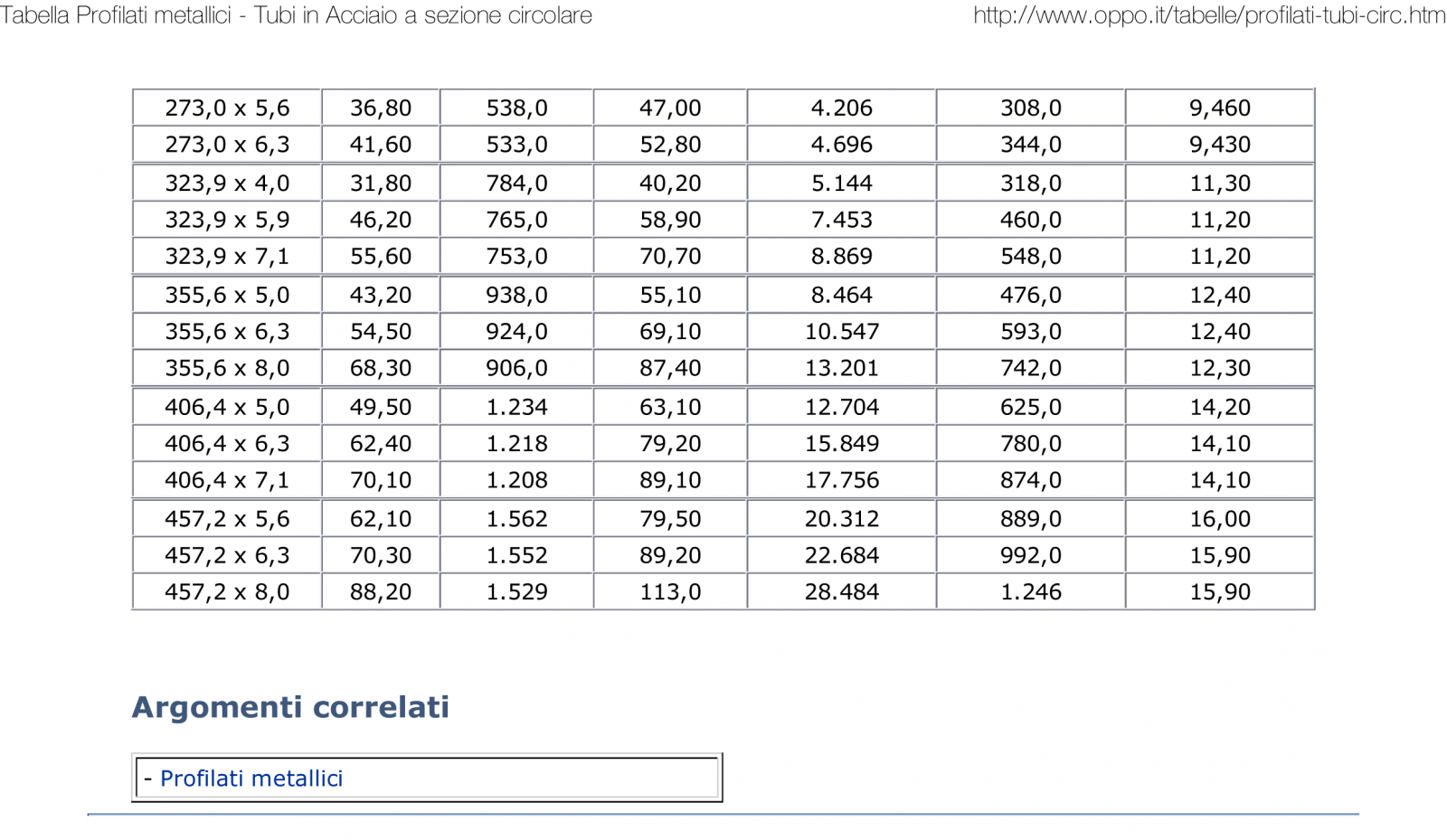
 e scelgo una sezione maggiore e la verifico dentro

Nbrd= χA fy_k/ γ

 

Infatti con un' area di 15,50 e un' Inerzia = 234 cm alla quarta,

ottengo un λ'= 0,83

un Ф= 0,9 circa

un χ= 0,81
 e finalmente un Nbrd= 328,821 kN che è maggiore della Nd!!!!!! risolto

 

 

 

Siti utili

http://www.oppo.it/tabelle/profilati-tubi-circ.htm

http://www.cpmsistemi.it/index1.htm

 

ESERCITAZIONE_ Ripartizioni forze sismiche

 

 

Scelta dell' impalcato:

 

  

    

 

 

 

 

 

 

 

 

 

 

 

 

 

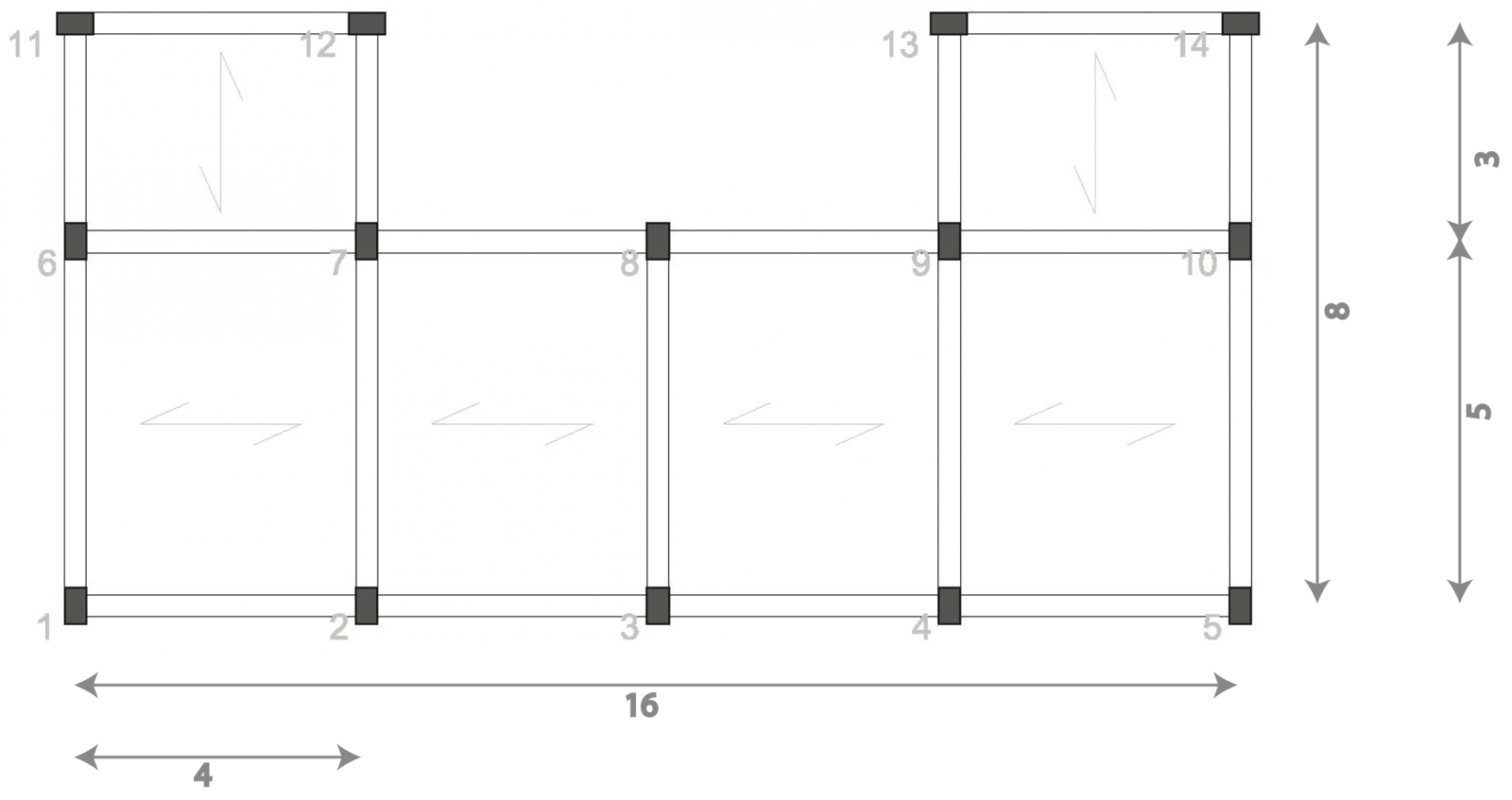
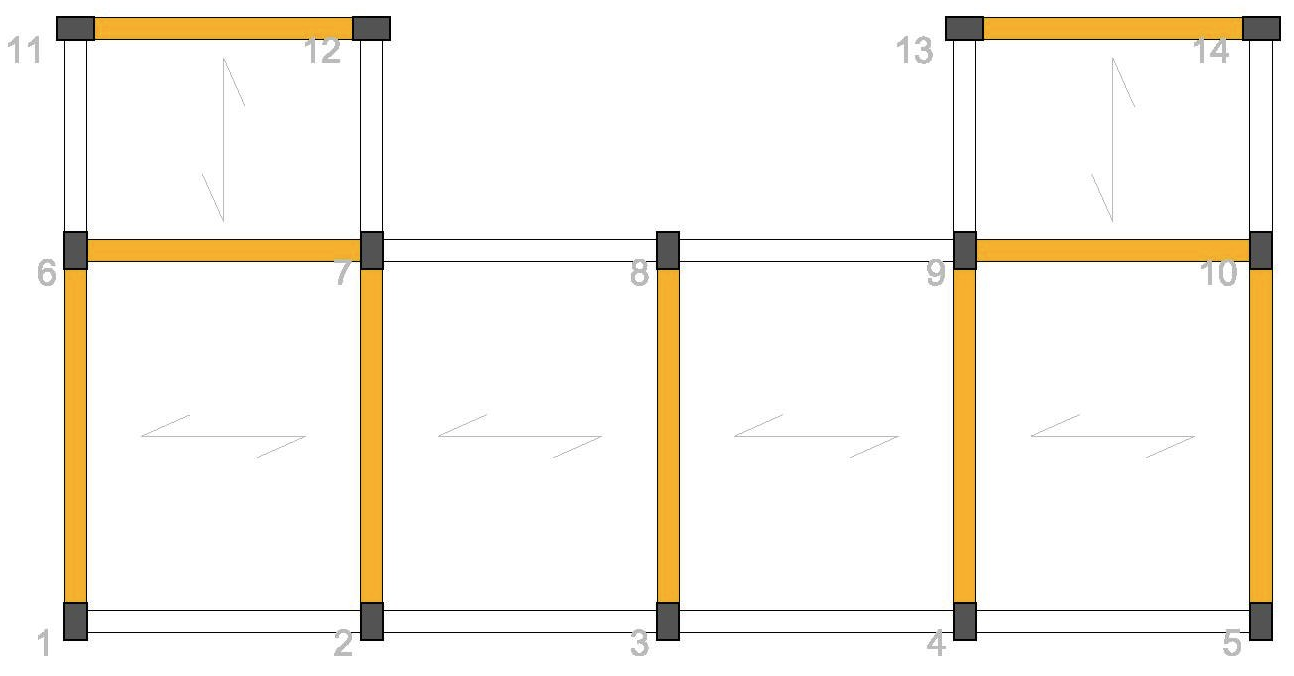
Struttura simmetrica a C con 6 campate e 9 controventi totali.

Il problema dell’equilibrio di questo corpo rigido in figura è che è 6 volte iperstatico.

Anziché risolverlo con il metodo delle forze possiamo risolverlo con un metodo che veda come incognite i parametri di spostamento.

Consideriamo che: dato che il corpo è rigido e piano, la sua cinematica dipende

solo da tre parametri:

1. la traslazione orizzontale do

2. la traslazione verticale dv

3. la rotazione f

QuindiI do, dv e f sono le incognite del problema. Per determinare il valore di questi parametri abbiamo a disposizione le tre equazioni di equilibrio di corpo rigido relative al nostro problema, facendo comparire in essa le 3 incognite.

 

 

 

STEP1_ calcolo rigidezze traslanti dei controventi dell' edificio.

 

Considereremo i vincoli dei controventi, non come carrelli, ma come molle per risolvere il problema dell' iperstaticità utilizzando la legge di Hooke:

 

F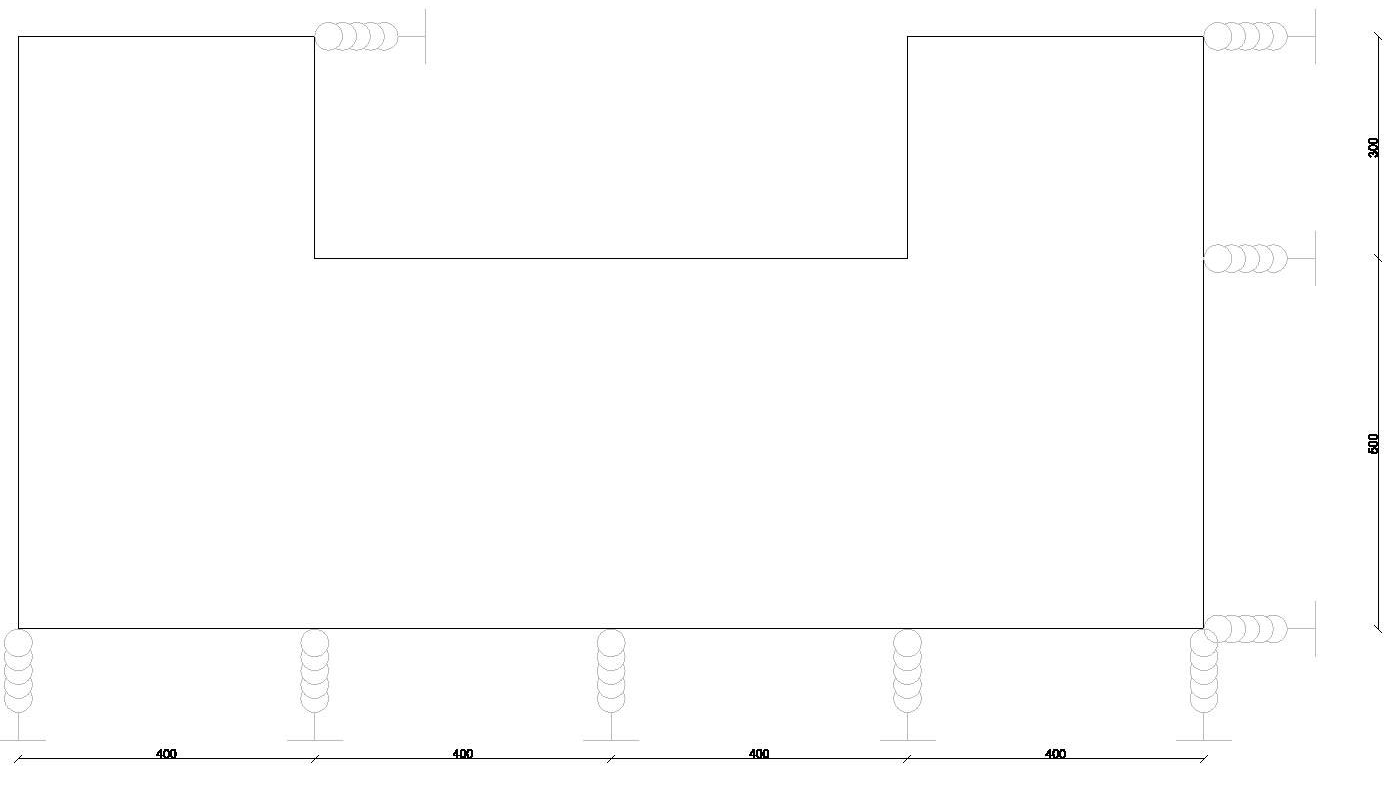= K d

 

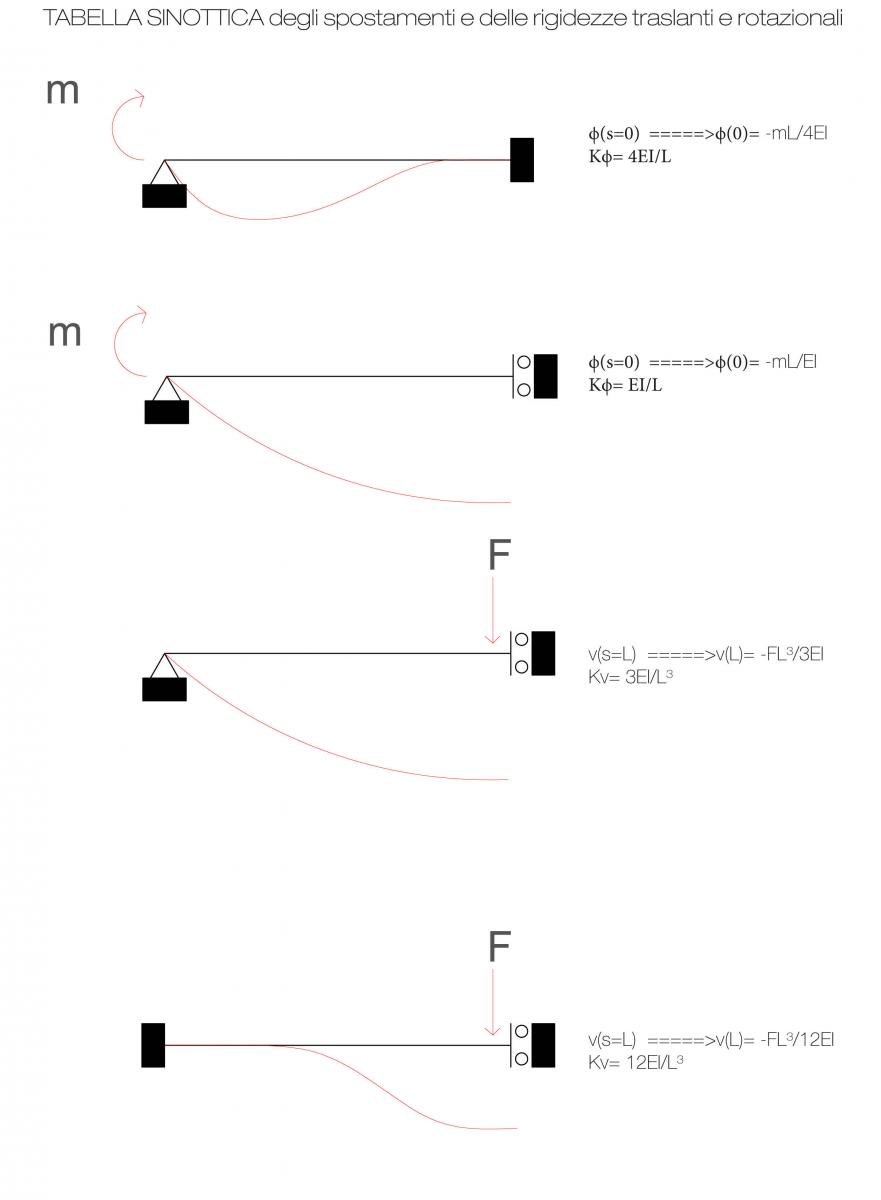
K è la rigidezza della molla che dipende dal tipo di struttura che si utilizza, se è uno shear type la rigidezza sarà 12EI/h³ in questi casi però, prendendo ad esempio il telaio 1-6-11, la rigidezza sarà data da:

 

12 E ( I1+ I6+I11)/ h³   =>Questo perchè i momenti d' inerzia sono differenti perchè si dispongono in base alla luce della trave.

 

 

 

Ovvero utilizzando come esempio sempre il controvento 1-6-11, i momenti d' inerzia del telaio sono:

 

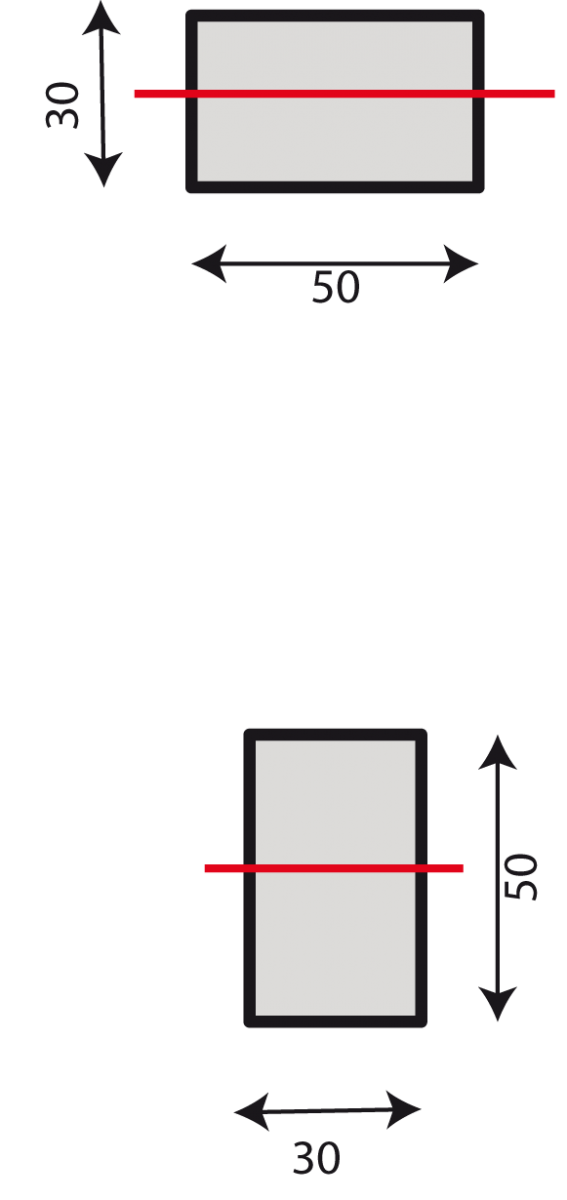
Pilastro 11: I= 50 x 30³/12= 112500 cm alla quarta

 

 

 

 

 

 

Pilastro 6-11: I=30 x 50³/12= 312500 cm alla quarta

 

 

 

Utilizzando il cemento armato il modulo di Young è 21000 N/mmq

Per cui Kt= 12 x 21000 ( 112500+ 312500+312500)/ (3,20)³= 56716,92 KN/m

 

 

 

 

Una volta spiegato il primo telaio il ragionamento vale identico per tutti gli altri:

 

     

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

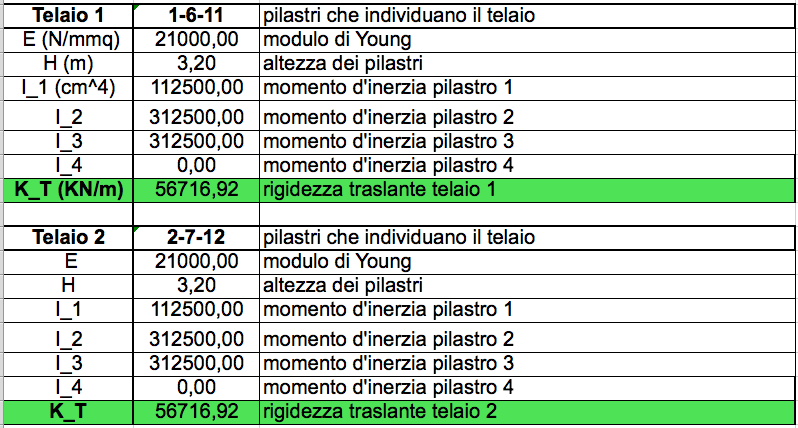
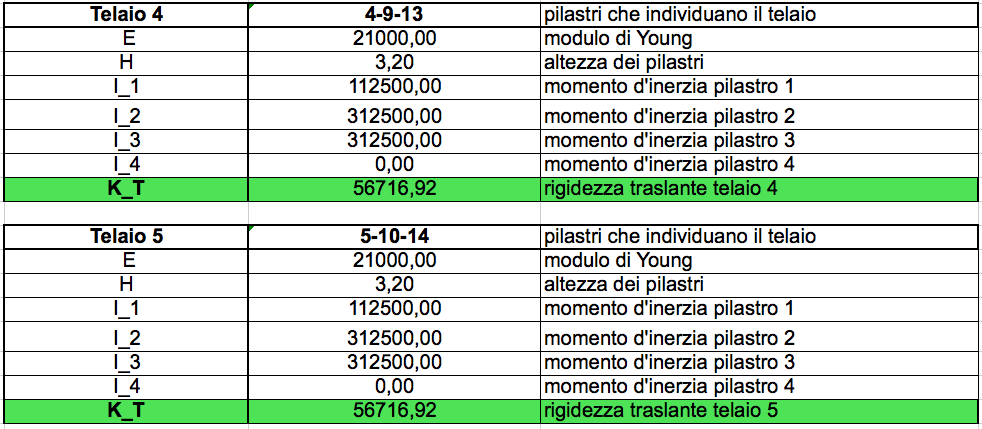
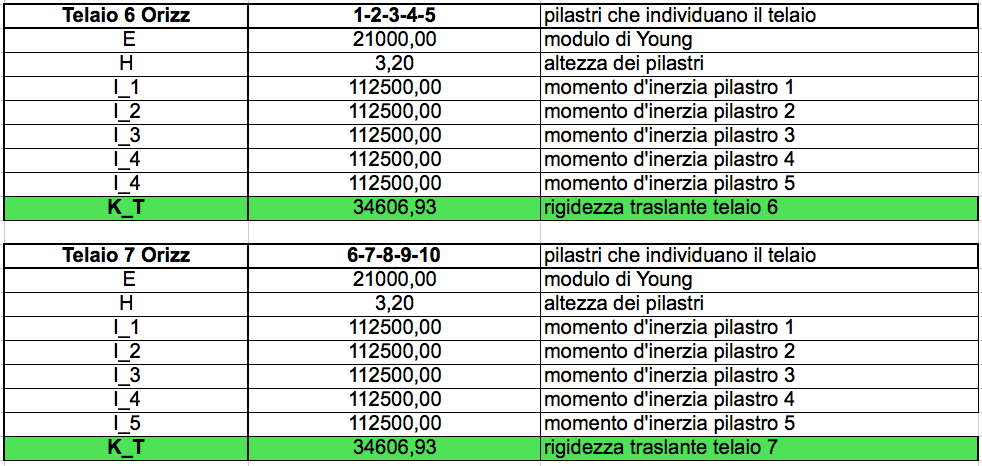
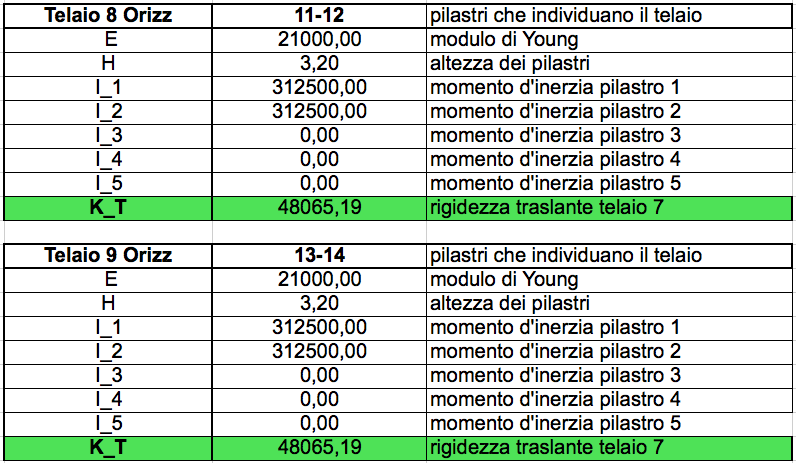
STEP2_ tabella sinottica controventi e distanze.

 

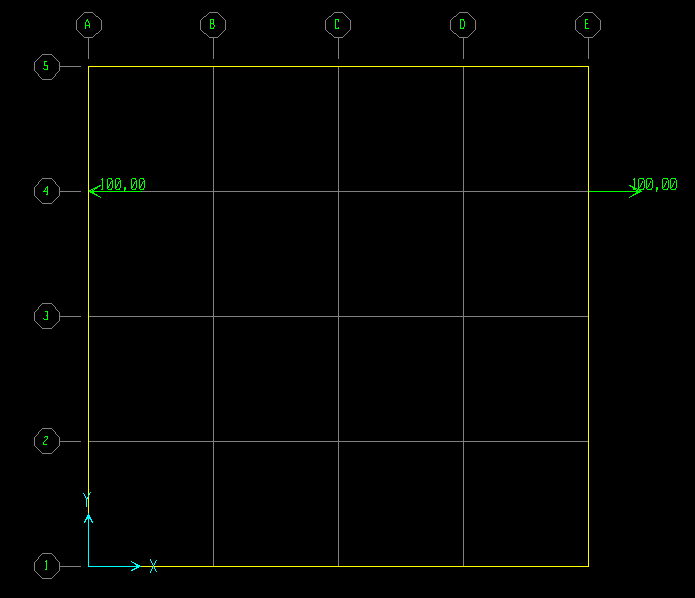
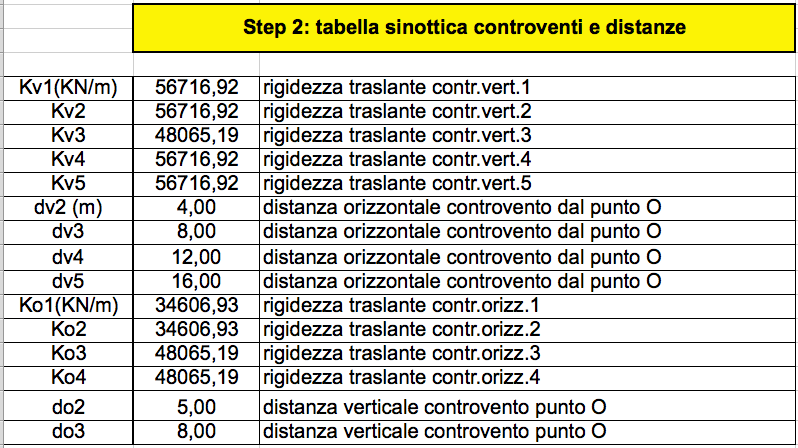Tabella che riassume ogni rigidezza dei controventi in base alle loro distanze dall' origine, per cui Kv1 (la rigidezza del telazio 1-6-11) dista dall' origine zero, perchè l' origine "o" è stata messa nel punto del pilastro 1 (come è possibile vedere nell' immagine sottostante), invece il telaio 2-7-12, ovvero Kv2, corrisponde alla distanza dv2 pari a 4 metri.

 

Per Kv s' intende la rigidezza verticale

Per Ku la rigidezza orizzontale

Per dv la distanza verticale

Per du la distanza orizzontale

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

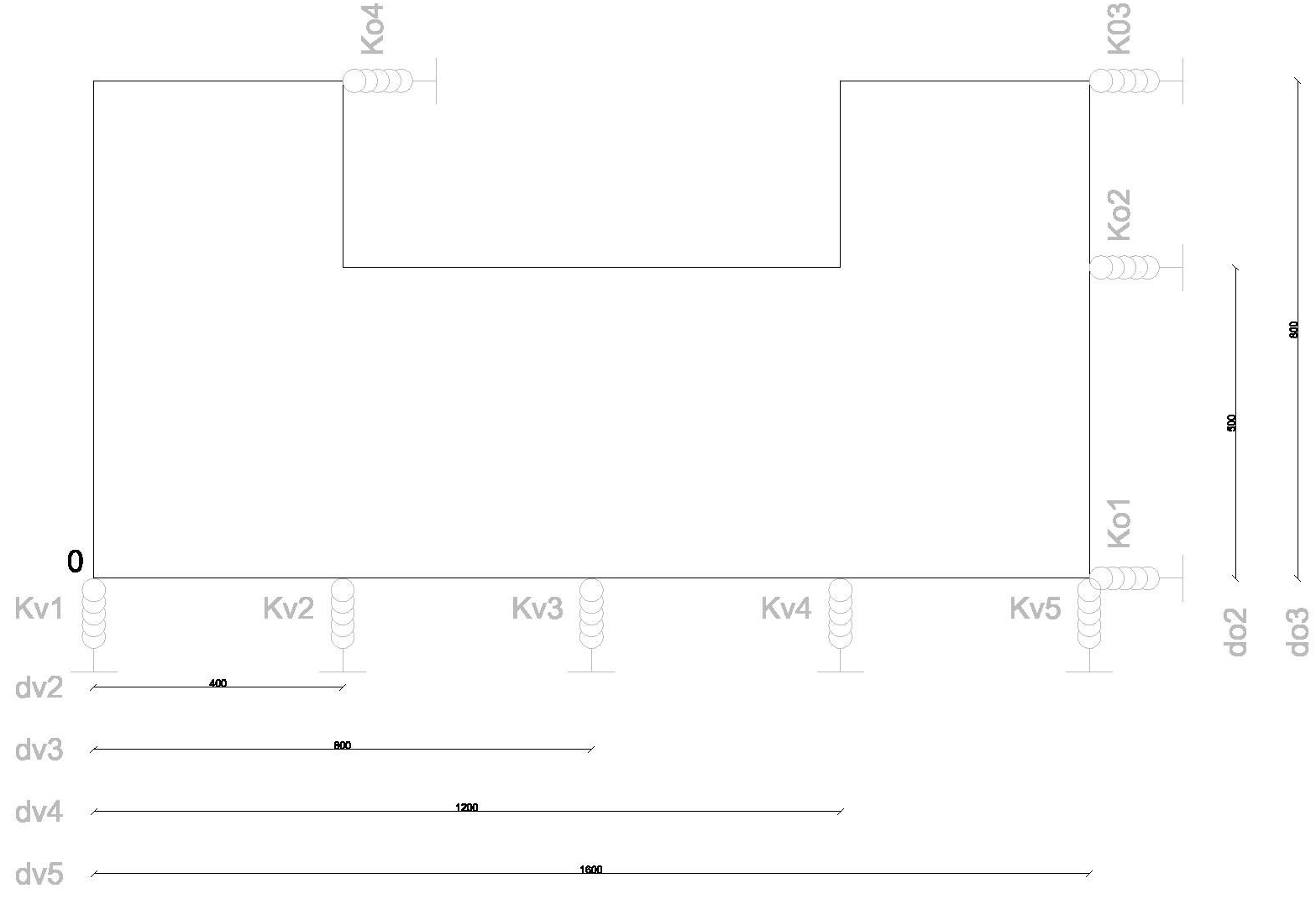
Step 3_ calcolo del centro di massa

 

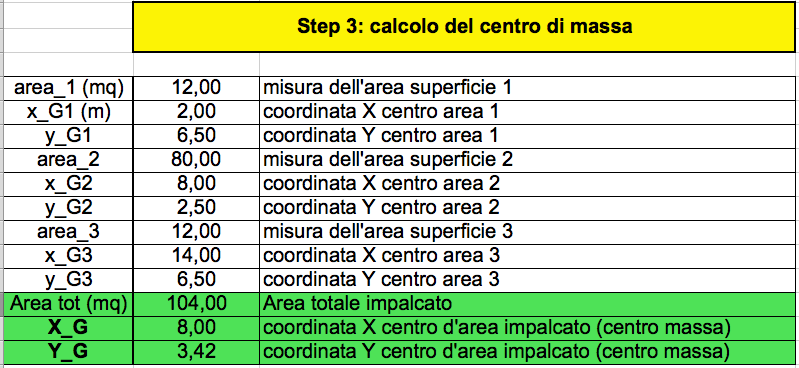In questa tabella si determinano le aree principali che compongono il nostro solaio, in questo caso ne abbiamo 3.

 

Ogni area ha 2 distanze che individuano il centro di massa di un area, ogni distanza Xg e Yg partono dall' origine "o", definita sopra (vedere figura sopra). Ovvero:

 

 

 

 

 

 

 

A1=4m x 3m=12 mq a cui corrisponde Xg1= 2m e Yg1= 6.50 m

 

A2= 16 x 5= 80 mq a cui corrisponde Xg2= 8m e Yg2= 2.50 m

 

A3=4m x 3m=12 mq a cui corrisponde Xg3= 14m e Yg3= 6.50 m

 

Mi posso quindi determinare il centro di massa dell' area totale con le coordinate Xgtot e Ygtot

 

Xgtot= (A1 x Xg1) +(A2 x Xg2) +(A3 x Xg3) / A1 + A2+ A3= 8 m

 

Ygtot= (A1 x Yg1) +(A2 x Yg2) +(A3 x Yg3) / A1 + A2+ A3= 3.42 m

 

 

Step 4: calcolo del centro di rigidezze e delle rigidezze globali

 

Determinazione delle rigidizze totali orizzontali e verticali:

Kvtot= Kv1+Kv2+Kv3+Kv4+Kv5= 274932,86

Kotot=Ko1+Ko2+Ko3+Ko4= 165344,24

 

Determinazione del centro delle rigidezze facendo:

X_C=(Kv1 x dv1)+ (Kv2 x dv2)+ (Kv3 x dv3)+ (Kv4 x dv4)+ (Kv5 x dv5)/ Kv tot= 8 m

 

Y_C=(Ko1 x do1)+ (Ko2 x do2)+ (Ko3 x do3)+ (Ko4 x do3)/ Kv tot =5.70m

 

Determinazione delle relative distanze dei controventi dal centro delle rigidezze:

 

 

 

 

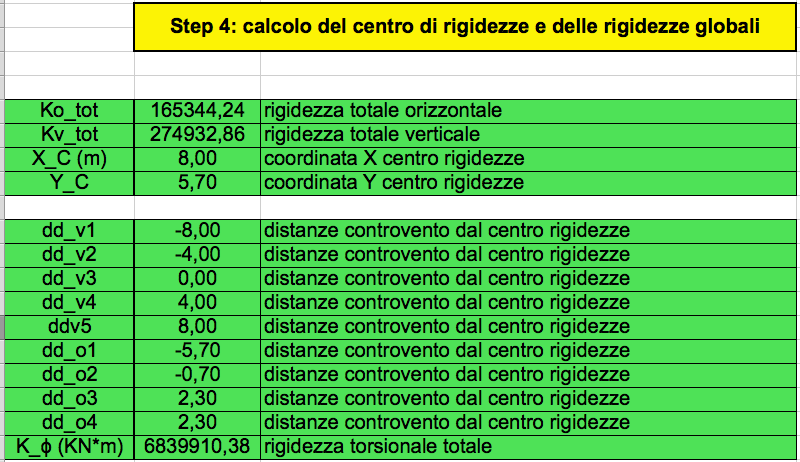
Le distanze ddv e ddo sono le distanze dei controventi dal cenrto di rigidezza.

 

Il valore della rigidezza torsionale è Kϕ= Σi Ki ddi²

 

 

 

 

 

 

 

Step 5_ analisi dei carichi sismici

 

Per capire questo step parto dal dire che la forza sismica è data da:

Fsismica= ma

m è la massa dell' edificio

 

a è una frazione dell' accelerazione della forza di gravità in cui:

a= c g c è un coefficiente <1

 

sostituisco e ottengo:

Fsismica= (m g) c in cui mg=Peso sismico

quindi F= cP oppure può essere scritto come Fsismica= cW

 

Per trovarmi W che è il peso sismico devo fare :

W= (G+Q)ψ

G= (qs+qp) Area tot

Q= qa Area tot

 

 

 

 

 

 

 

 

 

 

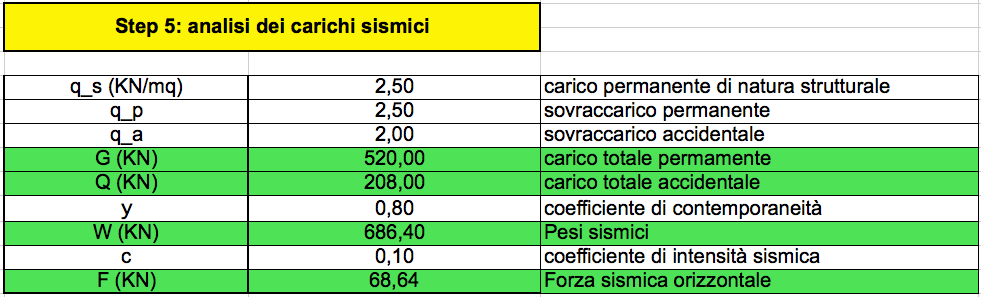
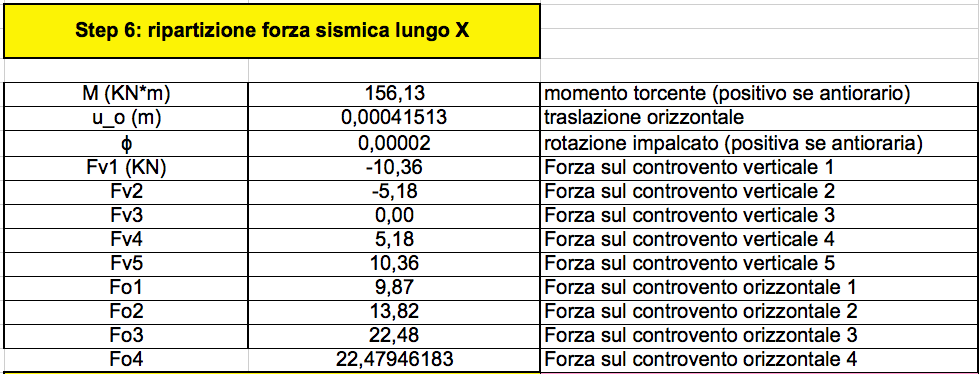
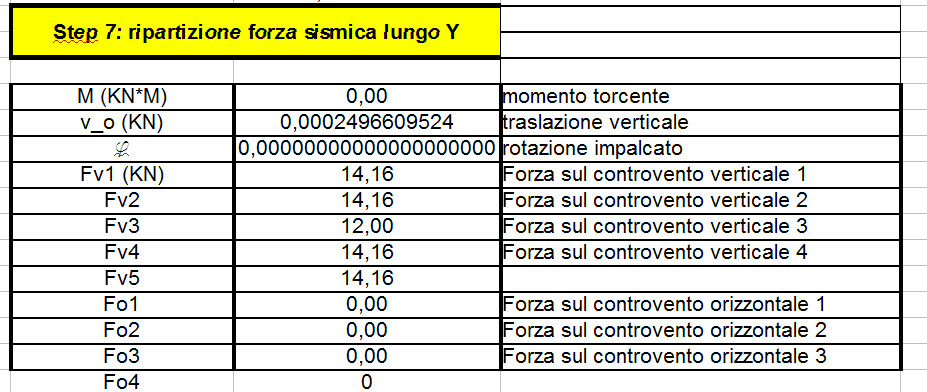
STEP 6 e 7_ ripartizioni forze sismiche lungo X e Y

Per il calcolo della ripartizione delle forse sismiche parto dal Calcolo del momento torcente, il quale, è il prodotto della forza sismica per il braccio, ( braccio è la distanza dal punto C al punto G).

!!Il momento torcente è utile per il calcolo della rotazione dell' impalcato!!!!

 

Mt= F (Yc-Yg) nel caso dello step 6

 

Mt= F (Xc-Xg) nel caso dello step 7

 

La traslazione orizzontale è:

Uo= Fsismica/Kotot

 

La traslazione verticale è:

Vo= Fsismica/Kvtot

 

Le reazioni vincolari si determinano:

Rio= Kio (Uo+φ dio)

Riv=Kiv( φ div)

 

  

 

 

 

 

 

 

 

 

 

ESERCIZIO_STRUTTURA CHIUSA

 

Una struttura chiusa senza cerniere interne è una struttura 3 volte iperstatica, se creiamo un "buco", ovvero una cerniera, nella struttura il sistema diventa isostatico.

Dove c' è una cerniera c' è un estremo libero in cui N=0, T=0 e M=0

 

 

 

 

 

Dati

F=100 KN

L=10 m                 

                                             

 

Divido il corpo in 3 parti, e assegno a ogni estremo delle cerniere delle ipotetiche reazioni vincolari:

 

Tratto AB

Equazione alla traslazione orizzontale (u)

u)xA-xB-F=0

Equazione alla traslazione verticale (v)

v)yB=yA

Equazione del momento con polo in "o"

o)yBL-xBL/2-FL/4=0

 

Tratto BC

v)yB=yC

u)xB=xC

o) -xCL/2 – yCL/2=0

 

Tratto CA

u) xC + F+ xA=0

v) yA=yC

o) FL/4 + xCL – yCL/2=0

 

 

 

Faccio un sistema delle equazione dei momenti, sopra scritti, per trovarmi le incognite "x" e "y".

 

o1)yBL-xBL/2-FL/4=0

o2)-xCL/2 – yCL/2=0 ======> yC=-xC ==> sostituisco questo valore dentro la terza

o3)FL/4 + xCL – yCL/2=0                              equazione, o3.

 

Ovvero:

o3)FL/4 + xCL – xCL/2=0 ====> xC=xB=yB=yC=yA= -F/6

Per trovare xA posso sostituire -F/6 dentro l' equazione l' equazione alla traslazione orizzontale:

u)xA-xB-F=0 e ottengo xA= 5F/6

 

DIAGRAMMI DELLE SOLLECITAZIONI

 

Sforzo Normale

 

 

 

 

 

 

 

 

Costante ovunque data la mancanza di carichi distribuiti e puntuali lungo l' asse interessato

 

 

 

 

 

 

 

 

Sforzo di Taglio e Momento

 

 

 

 

 

 

Costante ovunque, con dei salti nel diagramma del taglio nelle aste verticali dove è presente la forza puntuale F=100 che provoca un salto nel taglio pari ad F(100KN) e crea un punto di non derivabilità, ovvero uno spigolo, nel diagramma del momento.