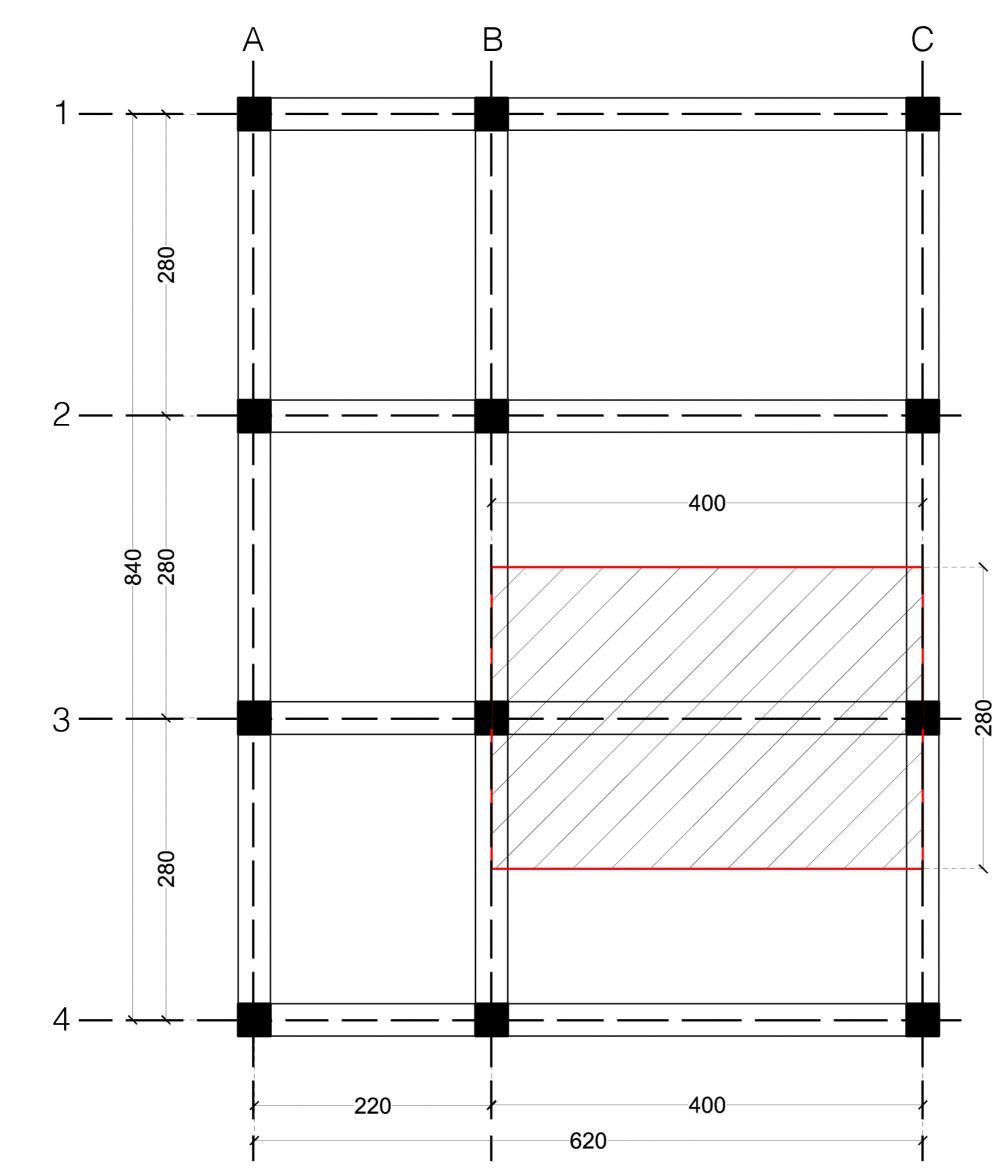
Ho preso in analisi la struttura del Laboratorio di Progettazione 1 (triennale). In particolare, una volta definito il telaio strutturale, ho scelto di progettare la trave del solaio sottoposta a maggior carico, ovvero la trave B-C lungo l’allineamento 3.
Su questa trave agisce una certa area di carico pari all’Area di Influenza:
A = luce x interasse = 4,00 m x 2,80m
Di seguito riporto la progettazione della trave, mediante il foglio di calcolo excel, nei 3 casi studiati (legno, acciaio, calcestruzzo armato).
Analisi dei carichi:
Con l’analisi dei carichi vogliamo sapere quanto pesa il solaio e quanto carico andrà sulla trave che stiamo analizzando. In particolare distinguiamo tra 3 tipologie di carico:
-
carico strutturale (qs = Kg/mq): comprende il peso proprio degli elementi strutturali.
-
sovraccarico permanente (qp = Kg/mq): tiene in considerazione il peso degli elementi non strutturali che compongono il pacchetto solaio come massetti, intonaci, pavimenti ma anche impianti.
-
sovraccarico accidentale (qa = Kg/mq): è legato alla funzione dell’edificio in quanto considera la variazione dei carichi mobili (arredi, persone,...) che possono esserci o meno durante l’esercizio della struttura.
Nella progettazione dobbiamo considerare la sommatoria di tutti i carichi previsti. Inoltre per poter progettare la trave principale dobbiamo tener conto, all’interno dei carichi strutturali, del peso dei travetti. È necessario, quindi, dimensionare prima i travetti del solaio tenendo conto di tutti i restanti carichi.
SOLAIO IN LEGNO

PROGETTO TRAVETTI con interassi di 1 m e luce di 2,80 m
Calcolo dei carichi:
1. carico strutturale, qs:
assito in legno: P = V x γ = volume x peso specifico = (0,035 m x 1 m x 1 m) x 6 KN/mc = 0,21 KN
qs = P/A = 0,21 KN / 1 mq = 0,21 KN/mq
Nel calcolare il volume dell'elemento strutturale, in questo caso l'assito, considero lo spessore dell'elemento e l'area di 1 mq.
2. sovraccarico permanente: qp = γ x h = peso specifico x spessore
pavimento in parquet: 8 KN/mc x 0,025 m = 0,20 KN/mq
massetto: 20 KN/mc x 0,03 m = 0,60 KN/mq
isolante acustico: 16 KN/mc x 0,04 m = 0,64 KN/mq
caldana: 10 KN/mc x 0,04 m = 0,40 KN/mq
impianti: 0,5 KN/mq
qp = 0,20 + 0,60 + 0,64 + 0,40 + 0,50 = 2,34 KN/mq
3. sovraccarico accidentale:
per una civile abitazione qa = 2 KN/mq
Utilizzo del foglio elettronico excel:
Tramite il foglio elettronico excel calcolo il carico totale a metro lineare che agisce sul travetto di progetto:
q = (qs + qp + qa) x i = (0,21 KN/mq + 2,34 KN/mq + 2 KN/mq) x 1 m = 4,55 KN/m
Successivamente impostando la dimensione della luce del travetto posso calcolarmi il momento massimo agente con il modello di una trave doppiamente appoggiata:
M = q x l2/8 = 4,55 KN/m x (2,80 m x 2,80 m) / 8 = 4,45 KN m
Se avessi preso in considerazione un modello statico differente avrei dovuto ricalcolare il momento (es. trave doppiamente appoggiata: M = q x l2 / 8).
Infine per definire le dimensioni della sezione del travetto devo calcolare la tensione di design, fD, tenendo conto del coefficiente kMOD che indica il degrado che la trave in legno subisce in funzione del tempo:
fD = kMOD x fk / γm = 0,5 x 28 N/mmq / 1,45 = 9,66 N/mmq
dove fk indica la tensione di snervamento e la imposto in base alla classe di legno scelta, in questo caso GL28h. Il valore γm rappresenta il coefficiente di sicurezza che tende a diminuire la resistenza di progetto e varia a seconda del materiale.
Ora inserendo il valore della base del travetto ottengo la sua altezza:
h = (6 x M x 1000 / b x fD) 0,5 = 16,65 cm
Approssimando le dimensioni così trovate ottengo un travetto di dimensioni 10x18 cm.
A questo punto effettuo nuovamente i calcoli con il foglio elettronico aggiungendo il carico dei travetti al carico strutturale per verificare il risultato precedentemente ottenuto:
qtr al metro lineare = A x γ = 0,1 m x 0,18 m x 6 KN/mc = 0,108 KN/m
qtr al metro quadro = qtr / interasse = 0,108 KN/m / 1 m = 0,108 KN/mq
qs = 0,21 KN/mq + 0,108 KN/mq = 0,318 KN/mq
Ottengo un’altezza pari a 16,84 cm quindi il dimensionamento precedentemente ipotizzato risulta corretto.

=> TRAVETTO IN LEGNO GL28h 10x18cm
PROGETTO TRAVI con interasse di 2,80 m e luce di 4 m
Applico lo stesso procedimento per il calcolo della trave principale:
1. calcolo dei carichi:
- carico strutturale, qs:
carico assito + carico travetti = 0,21 KN/mq + 0,108 KN/mq = 0,318 KN/mq
- sovraccarico permanente, qp: qp = 2,34 KN/mq
- sovraccarico accidentale, qa: qa = 2 KN/mq
2. calcolo carico totale al metro lineare:
q = (qs + qp + qa) x i = (0,318 KN/mq + 2,34 KN/mq + 2 KN/mq) x 2,8 m = 13,04 KN/m
3. calcolo del momento massimo agente:
M = q x l^2/8 = 13,04 KN/m x (4,00 m x 4,00 m) / 8 = 26,08 KN m
4. calcolo della tensione di progetto:
fD = kMOD x fk / 1,45 = 0,5 x 28 N/mmq / 1,45 = 9,66 N/mmq
5. calcolo dell'altezza:
h = (6 x M x 1000 / b x fD) ^ 0,5 = 28,47 cm -> trave 20x30 cm
6. verifico le dimensioni aggiungendo il carico dato dalla trave:
qtr al metro lineare = A x γ = 0,20 m x 0,30 m x 6 KN/mc = 0,36 KN/m
qtr al metro quadro = qtr / interasse = 0,36 KN/m / 2,80 m = 0,12 KN/mq
qs = 0,318 KN/mq + 0,12 KN/mq = 0,438 KN/mq
ottengo un'altezza pari a 28,83 cm quindi il dimensionamento della trave risulta corretto.
=> TRAVE IN LEGNO GL28h 20X30 cm
SOLAIO IN ACCIAIO
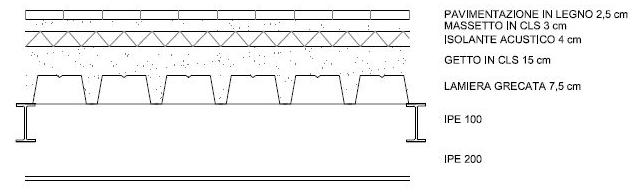
PROGETTO TRAVETTI con interasse di 1 m e luce di 2,80 m
Applico lo stesso procedimento svolto per la tipologia di solaio precedente:
1. calcolo dei carichi:
- carico strutturale, qs:
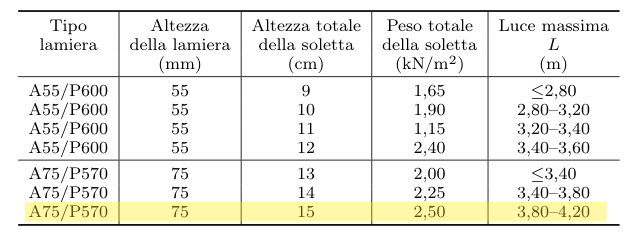
carico soletta in lamiera grecata e getto di calcestruzzo di 15 cm (valori tabellati) = 2,50 KN/mq
- sovraccarico permanente, qp:
pavimento in parquet: 8 KN/mc x 0,025 m = 0,20 KN/mq
massetto: 20 KN/mc x 0,03 m = 0,60 KN/mq
isolante acustico: 16 KN/mc x 0,04 m = 0,64 KN/mq
intonaco: 20 KN/mc x 0,015 = 0,30 KN/mq
impianti: 0,5 KN/mq
qp = 0,20 + 0,60 + 0,64 + 0,30 + 0,5 = 2,24 KN/mq
- sovraccarico accidentale, qa:
qa = 2 KN/mq
2. calcolo carico totale al metro lineare:
q = (qs + qp + qa) x i = (2,50 KN/mq + 2,24 KN/mq + 2 KN/mq) x 1 m = 6,74 KN/m
3. calcolo del momento massimo agente:
M = q x l2/8 = 6,74 KN/m x (2,80 m x 2,80 m) / 8 = 6,60 KN m
4. calcolo della tensione di progetto:
fD = fyk / 1,05 = 235 N/mmq / 1,05 = 223,81 N/mmq
5. calcolo del modulo di resistenza:
Wx = M /fD x 1000 = 29,51 cm3
6. dimensiono la trave:
ricerco sul profilario il Wx e definisco le dimensioni della sezione della trave
-> IPE 100 Wx = 34,2 cm3
7. verifico le dimensioni aggiungendo il carico della trave:
qtr al metro lineare (valore tabellato) = 0,08 KN/m
qtr al metro quadro = 0,086 KN/m / interasse = 0,086 KN/m / 1 m = 0,086 KN/mq
qs = 2,50 KN/mq + 0,086 KN/mq = 2,58 KN/mq
ottengo un W pari a 29,86 cm3 quindi il dimensionamento della trave risulta corretto.
=> TRAVETTO IN ACCIAIO S235 IPE100
PROGETTO TRAVI con interasse di 2,80 m e luce di 4,00 m
1. calcolo dei carichi:
- carico strutturale, qs:
carico soletta + carico travetto = 2,50 KN/mq + 0,08 KN/mq = 2,58 KN/mq
- sovraccarico permanente, qp:
- sovraccarico accidentale, qa:
qa = 2 KN/mq
2. calcolo carico totale al metro lineare:
q = (qs + qp + qa) x i = (2,58 KN/mq + 2,24 KN/mq + 2 KN/mq) x 2,80 m = 19,096 KN/m
3. calcolo del momento massimo agente:
M = q x l2/8 = 19,096 KN/m x (4,00 m x 4,00 m) / 8 = 38,192 KN m
4. calcolo della tensione di progetto:
fD = fyk / 1,05 = 235 N/mmq / 1,05 = 223,81 N/mmq
5. calcolo del modulo di resistenza:
Wx = M / fD x 1000 = 170,65 cm3
6. dimensiono la trave:
ricerco sul profilario il Wx e definisco le dimensioni della sezione della trave
-> IPE 200 Wx = 194,3 cm3
7. verifico le dimensioni aggiungendo il carico della trave:
qtr al metro lineare (valore tabellato) = 0,22 KN/m
qtr al metro quadro = 0,22 KN/m / interasse = 0,22 KN/m / 2,8 m = 0,07 KN/mq
qs = 2,58 KN/mq + 0,07 KN/mq = 2,65 KN/mq
ottengo un W pari a 172,40 cm3 quindi il dimensionamento della trave risulta corretto.
=> TRAVE IN ACCIAIO S235 IPE200
PROGETTO TRAVI con interasse di 2,80 m e luce di 4,00 m
Applico il procedimento utilizzato negli esempi precedenti:
1. calcolo dei carichi:
- carico strutturale, qs:
peso pignatte (sp. 12 cm) + peso caldana (sp. 4 cm) = 2,36 KN/mq (valore tabellato per una luce inferiore a 3,60 m).
- sovraccarico permanente: qp = γ x h = peso specifico x spessore
pavimento in parquet: 8 KN/mc x 0,025 m = 0,20 KN/mq
massetto: 20 KN/mc x 0,03 m = 0,60 KN/mq
isolante acustico: 16 KN/mc x 0,04 m = 0,64 KN/mq
impianti: 0,5 KN/mq
qp = 0,20 + 0,60 + 0,64 + 0,50 = 1,94 KN/mq
- sovraccarico accidentale:
per una civile abitazione qa = 2 KN/mq
2. calcolo carico totale al metro lineare:
q = (qs + qp + qa) x i = (2,36 KN/mq + 1,94 KN/mq + 2 KN/mq) x 1 m = 17,64 KN/m
3. calcolo del momento massimo agente:
M = q x l2/8 = 6,74 KN/m x (2,80 m x 2,80 m) / 8 = 35,28 KN m
4. calcolo della tensione di progetto dell'acciaio:
fD_f = fyk / 1,15 = 450 N/mmq / 1,15 = 391,30 N/mmq
Rispetto al calcolo del solaio in acciaio i valori presi in considerazione per definire la tensione di progetto dell'acciaio sono diversi. Infatti la classe di acciaio utilizzata per la realizzazione di solai in acciaio è differente rispetto a quella usata nei solai in cemento armato. L'acciaio da cemento armato ordinario comprende barre e reti e tralicci elettrosaldati del tipo B450A e B450C. Quest'ultima classe di acciaio deve essere obbligatoriamente utilizzata in zona sismica.
Nel calcolo effettuato ho quindi scelto la classe B450C che ha una resistenza di snervamento pari a 450 MPa e un limite di rottura di 540 MPa.
Inoltre, rispetto al calcolo per il solaio in acciaio, in questo caso varia anche il coefficiente di sicurezza, γm, pari a 1,15 trattandosi di acciaio da cemento armato.
5. calcolo della tensione di progetto del calcestruzzo:
fD_ca = fck / γm = 40 N/mmq / 1,75 = 22,86 N/mmq
fck = resistenza cilindrica del calcestruzzo. Ovvero viene calcolata la resistenza a compressione di un provino di forma cilindrica.
γm = coefficiente di sicurezza che per il calcestruzzo è pari a 1,75.
6. calcolo l'altezza utile:
l'altezza utile indica la distanza tra l'armatura tesa e il lembo compresso della sezione in cemento armato. Normalmente differisce dall'altezza effettiva della sezione per il valore del copriferro. Per definirla imposto una lunghezza di base di 25 cm.
hu = r √(M/ fD_c x b) = 17,70 cm
7. calcolo l'altezza minima:
dopo aver calcolato l'altezza utile della sezione posso ricavarmi l'altezza minima tenendo conto del valore del copriferro. Il copriferro indica una porzione di calcestruzzo, generalmente di pochi centimetri, la cui funzione è quella di proteggere i ferri dell'armatura dagli agenti atmosferici.
H = hu + c = 17,70 cm + 5 cm = 22,70 cm
ma i valori delle travi in cemento armato generalmente hanno un incremento consequenziale di 5 cm quindi si può arrotondare il valore così ottenuto dell'altezza a 25 cm.
Otterremmo in questo modo una trave quadrata che, però, non funziona bene dal punto di vista meccanico. Quindi devo necessariamente ricalcolare il valore dell'altezza utile ponendo b = 20 cm.
hu = 19,78 cm
H = 19,78 + 5 = 24,78 cm -> ho ottenuto una trave a sezione rettangolare 20x25 cm.
8. verifico le dimensioni:
Per effettuare una verifica del dimensionamento devo ricalcolare l'altezza della trave aggiungendo al valore dei carichi quello proprio della trave stessa.
qtr al metro lineare = A x 2500/100 = 1,24 KN/m
qtr al metro quadro = 1,24 KN/m / interasse = 1,24 KN/m / 2,80 m = 0,44 KN
qs = 2,36 KN + 0,44 KN = 2,80 KN
Ottengo una altezza minima pari a 25,46 cm quindi il dimensionamento precedente non è verificato e sarà necessario avere una trave 20X30 cm
=> TRAVE IN CEMENTO ARMATO 20X30 cm
ESERCITAZIONE 4_PIASTRA RETICOLARE SPAZIALE
Disegno, Analisi e Dimensionamento
DISEGNO IN AUTOCAD
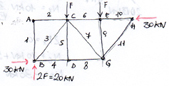
Disegno in autocad la piastra reticolare spaziale partendo da un modulo cubico di 2m x 2m x 2m.
Definisco un nuovo layar chiamandolo "ASTE" che comprenderà tutti gli elementi della struttura che vado a disegnare in modo tale che, importando il file in SAP, potrò assegnare al layar la funzione di Frames.
Inizio a disegnare dal punto di origine degli assi 0,0,0 in modo tale che importanto il disegno in SAP sia più semplice ritrovarlo nello spazio.

Definisco, quindi, in 2D le prime 3 aste del modulo reticolare e la sua diagonale, utilizzando un'unica polilinea. Non disegno l'intera faccia del modulo perchè, altrimenti, quando andrò ad utilizzare il comando Array/Serie avrei delle linee sovrapposte. Questo elemento è di fondamentale importanza perchè in caso di sovrapposizione di linee o di utilizzo del comando Copia avrei dei problemi nell'importazione del disegno in SAP.
A questo punto devo spostarmi dal piano in 2D allo spazio in 3D per andare a definire gli altri elementi del modulo cubico reticolare. Prima di fare ciò devo, però, ruotare la polilinea precedentemente definita lungo l'asse z. Per farlo utilizzo il comando Ruota3D.

Tramite questo comando possibile definire nello spazio l'asse di rotazione e l'angolo di rotazione. In questo caso imposto l'asse x come asse di rotazione e assegno un angolo di 90°.
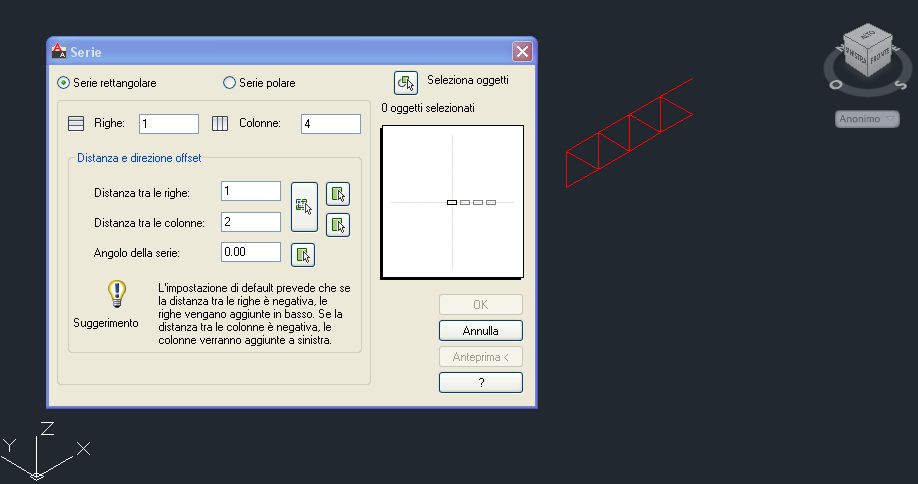
Per disegnare gli altri moduli della trave reticolare nello spazio utilizzo il comando Array/serie, prendendo come elemento di riferimento le aste disegnate fino ad ora. Il comando Array/serie permette di disegnare copie multiple di un oggetto in serie rettangolari o polari. è necessario quindi impostare i valori di questa serie. Nel nostro caso occorre definire una serie rettangolare formata da 1 riga e 4 colonne poste ad una distanza di 2 m (dimensione del modulo).
Si ottiene così la prima trave reticolare della piastra spaziale a cui manca, però, l'ultima asta verticale che non era stata disegnata nella polilinea iniziale per non creare sovrapposizioni e che ora è possibile definire attraverso una linea singola.
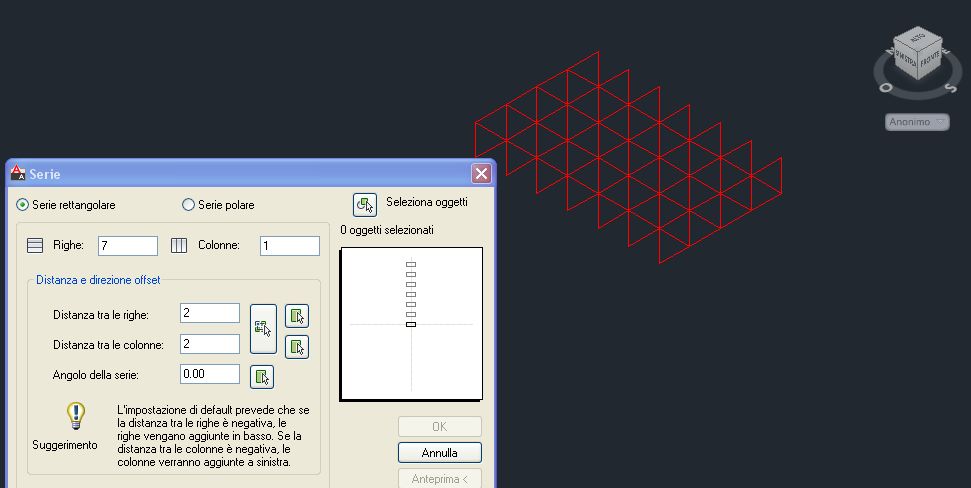
Una volta definiti i moduli della prima "riga" della piastra reticolare è necessario definire le rimanenti con il comando Array/Serie impostando 7 righe e 1 colonna ad una distanza di 2 m. Ottengo in questo modo tutte le travature reticolari complete della piastra lungo una direzione.

Per definire le travature reticolari lungo la direzione opposta devo disegnare il primo modulo lungo questa direzione e poi applicare nuovamente il comando Array/Serie. Per disegnare il primo modulo potrei modificare la posizione dell'UCS e utilizzare il comando polilinea ma per semplificare le operazioni utilizzo il comando Polilinea3D che assieme allo Snap ad oggetto 3D mi permette di disegnare nello spazio senza commettere errori.
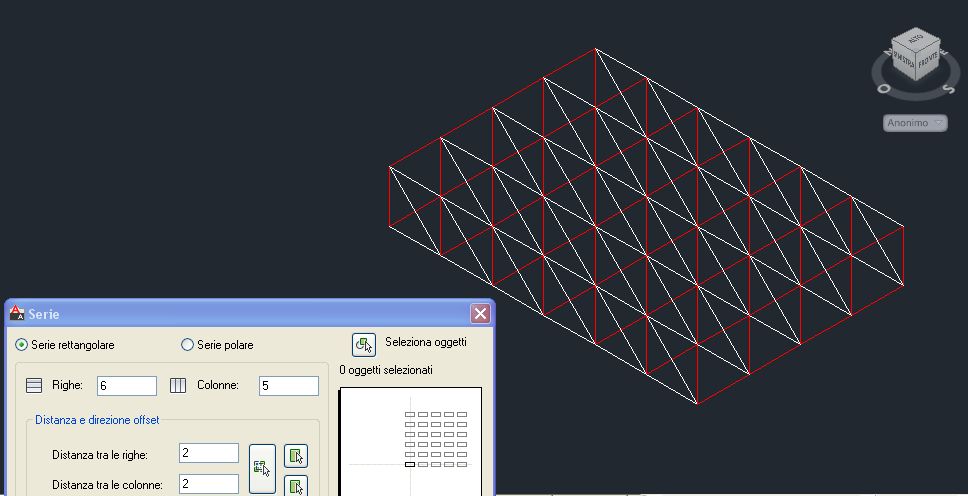
Applico l'Array/Serie per il modulo trasversale impostando 6 righe e 5 colonne a distanza di 2 m. Ottengo quindi una serie di travi reticolari in due direzioni opposte ortogonali l'una all'altra.

Gli ultimi elementi della piastra da definire sono le diagonali superiori e inferiori. Applico sempre lo stesso procedimento: disegno le diagonali sul primo modulo con il comando Polilinea3D e poi creo una serie con il comando Array/Serie lungo le due direzioni.
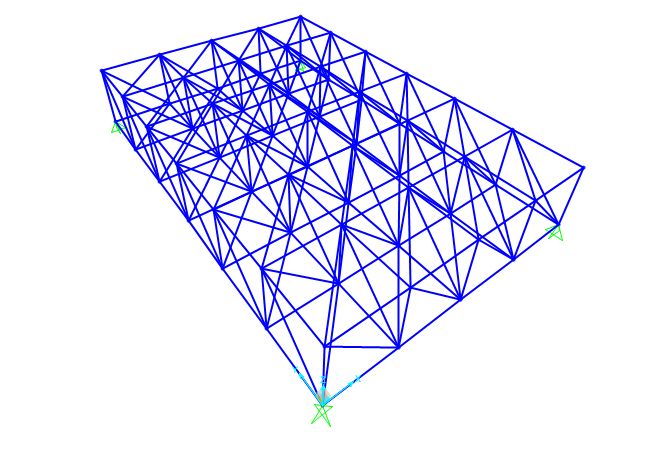
Il risultato finale è quello di una piastra reticolare spaziale asimmetrica formata da polilinee copiate e disposte in serie. Per importare il file su SAP devo esplodere le poliline ed esportare il file in formato .dxf2000.
Una volta aperto il file .dxf su SAP il programma chiede all'utente a quali elementi strutturali corrispondono eventuali layar. è quindi possibile, come detto in precedenza, assegnare al layar ASTE la funzione di FRAMES.
ANALISI IN SAP2000
In SAP per calcolare il comportamento della struttura è necessario: definire i vincoli, interni ed esterni, assegnare la sezione, il materiale e il carico.
- vincoli esterni:
selezionando i quattro vertici inferiore della piastra Ë possibile assegnare i vincoli esterni, le cerniere;
- vincoli interni:
le aste delle travature reticolari sono incernierate tra di loro e non incastrate quindi occorre definire il rilascio dei momenti in tutte le aste definendo così la presenza di cerniere interne. Attraverso il percorso "Select All -> Assign -> Frame -> partial fixity -> Assign frame releases" si impone il rilascio dei momenti alla fine e all'inizio di tutte le aste selezionate.
- materiale e sezione:
è necessario prima definire il materiale e la sezione dell'asta e solo successivamente assegnare queste caratteristiche alle aste della struttura.
Per definire il materiale alla struttura è sufficiente seguire il percorso "Define->material->New material" e creare il materiale "acciaio".
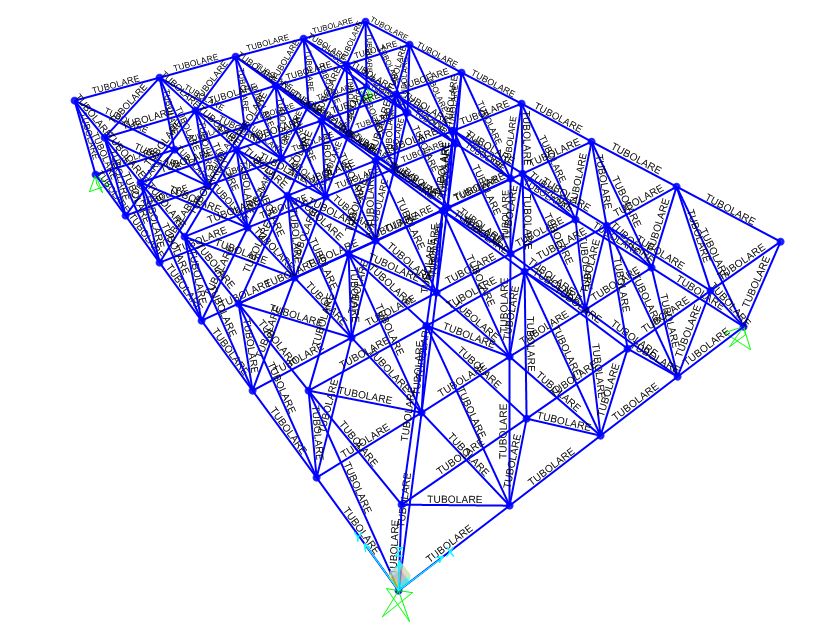
La sezione viene definita attraverso un percorso analogo "Define->Section properties->frame section" scegliendo la sezione tubolare/pipe. Inoltre nel creare una nuova sezione è necessario assegnare ad essa anche il materiale corrispondente, quindi in questo caso l'acciaio. Successivamente le proprietà così definite devono essere assegnate alla struttura tramite il percorso "Assign->Frame->Frame section" selezionando tutte le aste della piastra.
- carico:
allo stesso modo delle caratteristiche della sezione anche il carico deve essere prima definito e poi assegnato alla struttura. è possibile definirlo seguendo "Define->load pattern" creando una "forza concentrata". In seguito questa forza deve essere assegnata su tutti i nodi superiori della piastra.
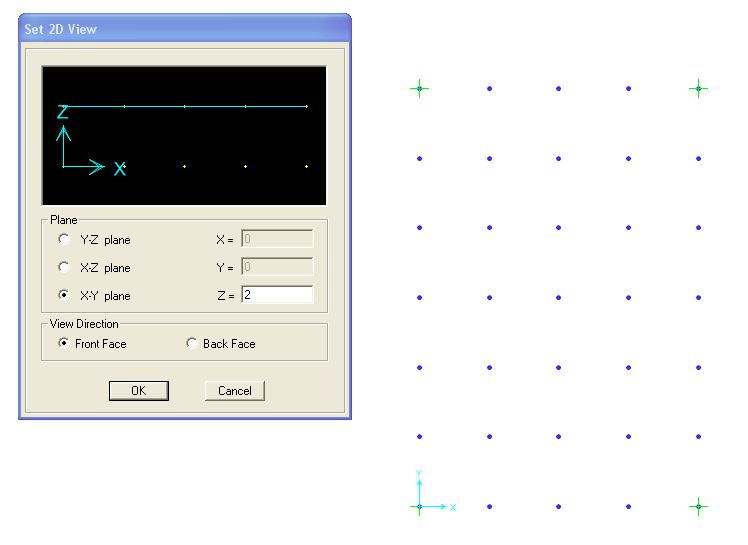
Per selezionare i nodi superiorie è necessario "spegnere" momentaneamente le aste della struttura tramite "Set display options" selezionando "Frame not in view" e "Joints not invisible". In seguito tramite "View->Set 2D view" è possibile selezionare gli elementi che si vogliono vedere e quindi seleziono la parte superiore della piastra in 2D. Così tornando alla vista superiore della piastra, selezionando tutti i nodi sono certa di tenere in considerazione solo quelli superiori. A questo punto con "Assign" ottengo la disposizione della forza concentrata precedentemente definita su tutti i nodi superiori.
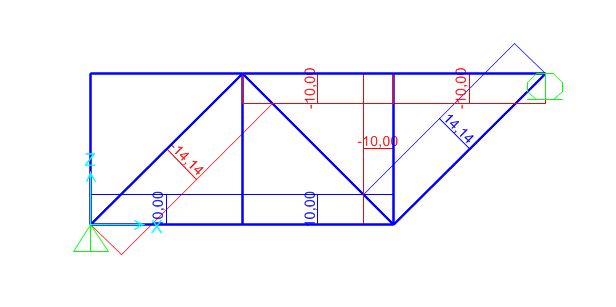
La struttura è totalmente definita in SAP ed è quindi possibile lanciare l'analisi. In questo modo ottengo il grafico della deformata della piastra e soprattutto i diagrammi dello sforzo normale che agisce su tutte le aste.
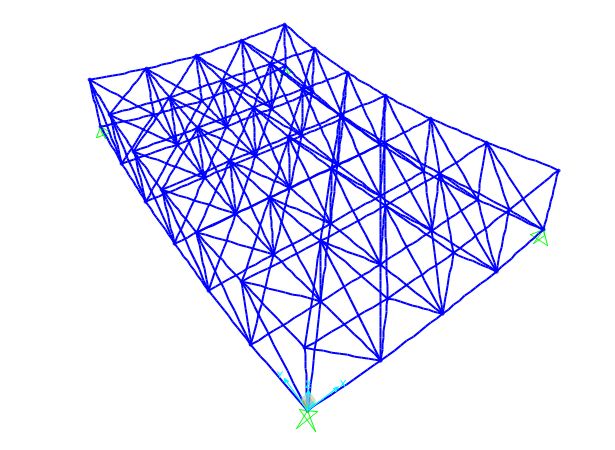

In particolare tramite le tabelle generate da SAP è possibile definire il valore dello sforzo normale di compressione e di trazione massimo e su quali aste questi valori agiscono. Per ottenere le tabelle è sufficiente seguire il percorso "Display->Show Tables" e selezionare "Elements Output" per ottenere tutti le caratteristiche geometriche e meccaniche riguardanti le aste.
PROGETTO A TRAZIONE E COMPRESSIONE DELLE ASTE
Da SAP ottengo:
Nmax di compressione = 307,254 KN sull'asta 271
Nmax di trazione = 258,934 KN sull'asta 287
- progetto a trazione:
sapendo che fD = N / A posso ricavarmi l'area di progetto A=N/fD
dove fD = fy/γm
fy = resistenza a snervamento
γm = coefficiente di sicurezza
fD = 275 MPa/1,05 = 261,9 MPa
ottendo quindi un valore della tensione di progetto che è minore rispetto a quello della resistenza dell'acciaio avendo inserito il coefficiente di sicurezza imposto dalla normativa.
Posso quindi calcolare l'area di progetto:
A = Nmax di trazione / fD = 258934 N / 261,9 N/mm2 = 988,6 mm2 = 9,88 cm2
Nel profilario dei tubi in acciaio a sezione circolare cerco un profilo tale che la sua area sia maggiore o uguale a quella appena calcolata:
scelgo quindi il profilo di dimensioni 88,9x4,0 mm con area pari a 10,70 cm2 > 9,88 cm2.
- progetto a compressione:
il procedimento per il progetto a compressione è uguale a quello a trazione:
A = Nmax di compressione / fD = 307254 N / 261,9 N/mm2 = 1173,17 mm2 = 11,73 cm2
scelgo quindi per l'asta compressa un profilo circolare 114,3x3,6 mm con un'area di 12,50 cm2.
Ma per il progetto a compressione, a differenza di quello a trazione, è necessario effettuare due verifiche quella a snellezza e quella a stabilità. Nella compressione è insito, infatti, il rischio dell'instabilità euleriana dovuta all'eccesso di snellezza dell'elemento. L'intabilità euleriana indica quando un elemento strutturale, soggetto a compressione, si inflette e sbanda a causa della sua snellezza. Per snellezza si intende quando il rapporto tra altezza e lunghezza dell'oggetto è molto grande.
Ncr = π2 x E x Jmin / l02
dove E = modulo elastico a compressione
Jmin = momento di inerzia minimo della sezione che ricavo dal profilario.
l0 = luce libera di inflessione, ovvero quanto è larga l'onda sinusoidale che definisce lo sbandamento, dipende quindi dai vincoli. Nel caso dell'asta reticolare i vincoli sono una cerniera e un carrello quindi l0 = l. In particolare, l'asta con sforzo normale maggiore è una diagonale quindi l = √2 m = 2,8 m.
Ncr = π2 x 210000 N/mm2 x 1920000 mm4 / 7840000 mm2 = 500000 N = 500 KN
1. verifica a snellezza:
λ = l0 / ϱ < 200
dove l0 = luce libera di inflessione
ϱ = raggio di inerzia che in fase di verifica ricavo dal profilario
λ = 280 cm / 3,92 cm = 71,42 < 200 -> verificato
2. verifica a stabilità:
Nd > Nbdr
dove Nbdr = resistenza all'instabilità = χ A fyk / γm
χ = 1 / (φ + √φ2-λ2) < 1
φ = 0,5 [1 + α (λ - 0.2) + λ2]
α = fattore di imperfezione = 0,21
per sezioni cave formate a caldo
λ = √(A x fyk / Ncr)
Ottengo quindi Nbrd = 424,443 KN > 307,254 NN -> verificato
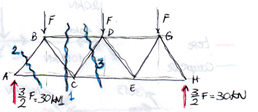
ESERCITAZIONE 5_RIPARTIZIONE DELLE FORZE SISMICHE
Una struttura deve essere vincolata non solo per i carichi verticali ma anche per quelli orizzontali. Per analizzare l’azione di una forza orizzontale su di una struttura dobbiamo avanzare due ipotesi:
1) il solaio deve essere considerato come un diaframma abbastanza rigido in modo tale da comportarsi come corpo rigido. I movimenti permessi ad un corpo rigido sono: la traslazione orizzontale, la traslazione verticale e la rotazione che, in particolare, dipende dalla disposizione della rigidezza in pianta dei controventi;
2) i telai devono comportarsi come corpi elastici, ovvero come delle molle che si deformano assorbendo il carico orizzontale, per poi restituirlo sotto forma di forza di richiamo.
Ho, dunque, una forza orizzontale che agisce nel centro di massa della struttura e che dovrebbe far traslare il corpo rigido, ma nel caso in cui si hanno delle rigidezze diverse nei controventi si genera una rotazione attorno al centro delle rigidezze della struttura. La distribuzione in pianta delle rigidezze è di fondamentale importanza nell’analisi delle forze sismiche poichè si avrà una rotazione della struttura nel caso in cui il centro delle rigidezze non sia coincidente con il centro della massa della struttura stessa. In questo caso, infatti, si crea un braccio tra la forza esterna e la risultante delle forze di richiamo dei controventi, che generano un momento.
Ho scelto di esaminare di seguito, con il foglio excell, la struttura di un impalcato di 17 pilastri con 4 controventi verticali e 5 orizzontali, in calcestruzzo armato.

STEP_1: calcolo delle rigidezze traslanti dei controventi dell’edificio
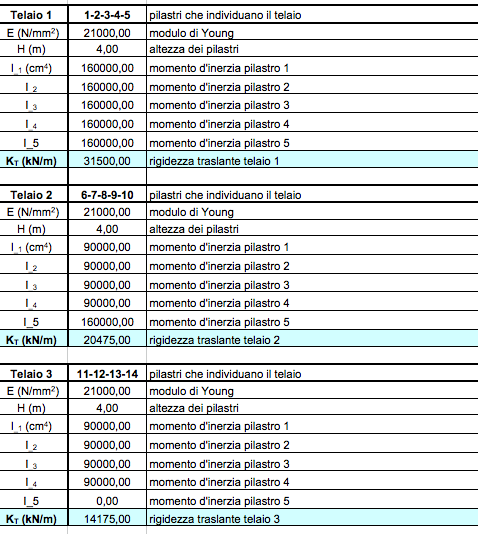
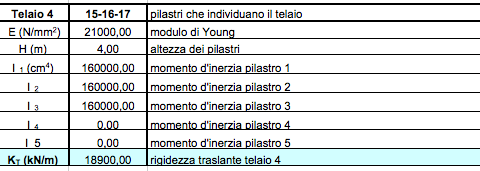
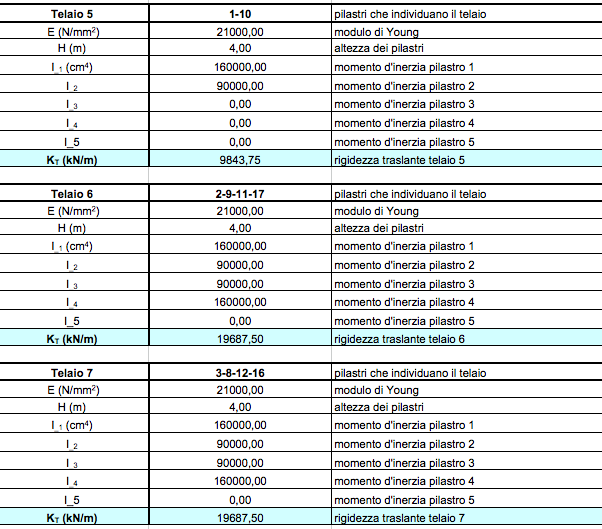
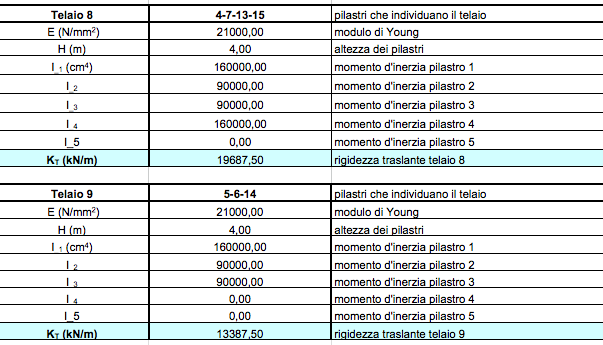
Il primo passo è quello di analizzare singolarmente ogni telaio della struttura, per calcolare la rigidezza traslante di ogni controvento. In particolare
kt = (12 E ΣiJi) / h3
dove E = modulo di Young = 21000 N/mm2 per il calcestruzzo
h = altezza dei pilastri
ΣiJi = sommatoria dei momenti di inerzia di pilastri del telaio.
Con la sommatoria si tiene conto della possibilità che pilastri dello stesso telaio possano avere momenti di inerzia differenti legati al fatto che oltre a svolgere la funzione di controvento devono anche portare il solaio.

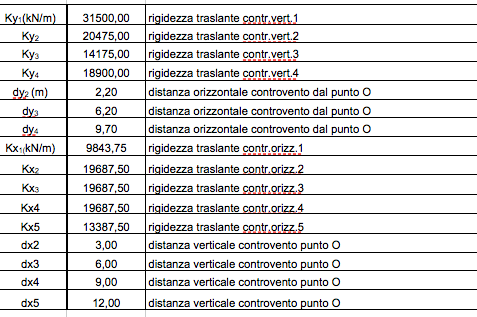
STEP_2: tabella sinottica
tabella riassuntiva in cui sono riportate le rigidezze calcolate precedentemente e le distanze calcolate rispetto al punto O.
STEP_3: calcolo del centro delle masse
La forza orizzontale viene applicata al centro di massa che è posto sugli impalcati perchè su di essi agiscono tutti i carichi e corrisponde al centro delle aree. Si calcolano quindi prima le aree e le coordinate dei rispettivi centri d’area calcolati rispetto il punto O.
XG = (A1 xG1 + A2 xG2 + A3 xG3) / (A1 + A2 + A3)
YG = (A1 yG1 + A2 yG2 + A3 yG3) / (A1 + A2 + A3)

STEP_4: calcolo del centro delle rigidezze e delle rigidezze locali
Calcolo le coordinate del centro delle rigidezze:
Xc = Σi kvdv / kv tot.
Yc = Σi kodo / ko tot.
dove d indica la distanza dei controventi dal centro delle rigidezze, perchè C è il punto attorno al quale il corpo ruota se la forza orizzontale è applicata nel centro di massa non coincidente con il centro delle rigidezze. Quindi il centro delle rigidezze è posto vicino al controvento più rigido. Inoltre le distanze hanno un segno perchè a seconda di dove sono posti i telai ho, rispetto a C, una rotazione oraria o antioraria.
Calcolo anche la rigidezza torsionale totale, kΦ = Σiki ddi2
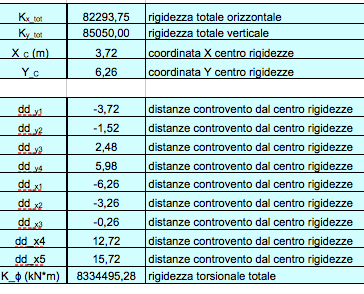
STEP_5: analisi dei carichi sismici
La forza sismica è data dal prodotto della massa dell’edificio e dell’accelerazione di trascinamento del suolo. Quest’ultimo valore è dato dalla normativa e corrisponde ad una frazione dell’accelerazione di gravità.
F = m a
a = c g dove c < 1 che corrisponde al coefficiente di intensità sismica.
quindi F = m c g = c (mg) dove mg = Peso
--> F = c P
La forza sismica è una frazione della forza peso, quindi, più un elemento è pesante e più è vulnerabile alla forza sismica.
Calcoliamo quindi il peso della struttura dopo aver definito i carichi strutturali, accidentali e permanenti che agiscono sulla struttura.
P = G + ψ Q dove G = carico totale permanente = (qs + qp) Atot
ψ = coefficiente di contemporaneità, dato dalla normativa, che diminuisce il carico accidentale.
Q = carico totale accidentale = qa Atot

STEP_6: ripartizione della forza sismica lungo x e lungo y
Analizziamo la ripartizione della forza sismica lungo entrambe le direzioni in quanto l’azione del sisma è particolarmente incerta ed aleatoria. Infatti, oltre a non sapere quando capiterà un episodio sismico è impossibile definire anche la direzione in cui avverrà. Inoltre la forza sismica non è mai applicata nel centro delle rigidezze e sviluppa quindi un momento torcente che provoca la rotazione dei controventi in entrambe le direzioni.
Calcoliamo quindi anche il momento torcente nelle due direzioni:
M = F (XC - XG)
M = F (YC - YG)
dove (YC - YG) è il braccio della forza, ovvero la distanza tra la coordinata Y del centro delle rigidezze e quella del centro di massa.
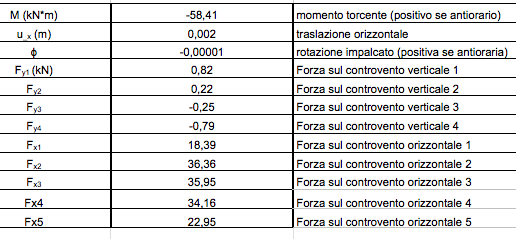
Dopo aver calcolato il momento torcente, la traslazione (orizzontale e verticale) e la rotazione è possibile definire come la forza sismica si ripartisce su ogni controvento in base alla rigidezza dei controventi stessi:
FxO= KxO(ux+ ϕdxO) per i controventi orizzontale
FyO= KyO(uy+ ϕdyO) per i controventi verticali
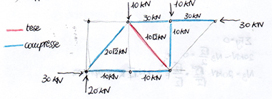
Ripartizione della forza sismica lungo Y:
Ripartizione della forza sismica lungo X:
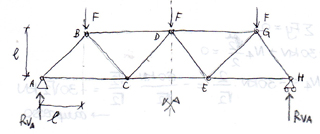
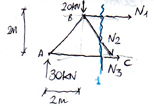
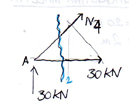
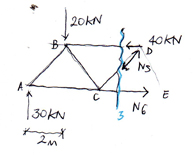
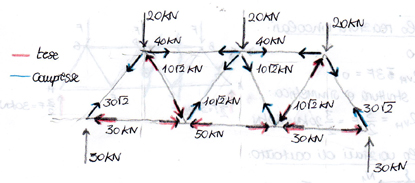



 nodo A:
nodo A:












 Per disegnare gli altri moduli della trave reticolare nello spazio utilizzo il comando Array/serie, prendendo come elemento di riferimento le aste disegnate fino ad ora. Il comando Array/serie permette di disegnare copie multiple di un oggetto in serie rettangolari o polari. è necessario quindi impostare i valori di questa serie. Nel nostro caso occorre definire una serie rettangolare formata da 1 riga e 4 colonne poste ad una distanza di 2 m (dimensione del modulo).
Per disegnare gli altri moduli della trave reticolare nello spazio utilizzo il comando Array/serie, prendendo come elemento di riferimento le aste disegnate fino ad ora. Il comando Array/serie permette di disegnare copie multiple di un oggetto in serie rettangolari o polari. è necessario quindi impostare i valori di questa serie. Nel nostro caso occorre definire una serie rettangolare formata da 1 riga e 4 colonne poste ad una distanza di 2 m (dimensione del modulo).
 Una volta definiti i moduli della prima "riga" della piastra reticolare è necessario definire le rimanenti con il comando Array/Serie impostando 7 righe e 1 colonna ad una distanza di 2 m. Ottengo in questo modo tutte le travature reticolari complete della piastra lungo una direzione.
Una volta definiti i moduli della prima "riga" della piastra reticolare è necessario definire le rimanenti con il comando Array/Serie impostando 7 righe e 1 colonna ad una distanza di 2 m. Ottengo in questo modo tutte le travature reticolari complete della piastra lungo una direzione. Per definire le travature reticolari lungo la direzione opposta devo disegnare il primo modulo lungo questa direzione e poi applicare nuovamente il comando Array/Serie. Per disegnare il primo modulo potrei modificare la posizione dell'UCS e utilizzare il comando polilinea ma per semplificare le operazioni utilizzo il comando Polilinea3D che assieme allo Snap ad oggetto 3D mi permette di disegnare nello spazio senza commettere errori.
Per definire le travature reticolari lungo la direzione opposta devo disegnare il primo modulo lungo questa direzione e poi applicare nuovamente il comando Array/Serie. Per disegnare il primo modulo potrei modificare la posizione dell'UCS e utilizzare il comando polilinea ma per semplificare le operazioni utilizzo il comando Polilinea3D che assieme allo Snap ad oggetto 3D mi permette di disegnare nello spazio senza commettere errori.  Applico l'Array/Serie per il modulo trasversale impostando 6 righe e 5 colonne a distanza di 2 m. Ottengo quindi una serie di travi reticolari in due direzioni opposte ortogonali l'una all'altra.
Applico l'Array/Serie per il modulo trasversale impostando 6 righe e 5 colonne a distanza di 2 m. Ottengo quindi una serie di travi reticolari in due direzioni opposte ortogonali l'una all'altra. Gli ultimi elementi della piastra da definire sono le diagonali superiori e inferiori. Applico sempre lo stesso procedimento: disegno le diagonali sul primo modulo con il comando Polilinea3D e poi creo una serie con il comando Array/Serie lungo le due direzioni.
Gli ultimi elementi della piastra da definire sono le diagonali superiori e inferiori. Applico sempre lo stesso procedimento: disegno le diagonali sul primo modulo con il comando Polilinea3D e poi creo una serie con il comando Array/Serie lungo le due direzioni.






 In particolare tramite le tabelle generate da SAP è possibile definire il valore dello sforzo normale di compressione e di trazione massimo e su quali aste questi valori agiscono. Per ottenere le tabelle è sufficiente seguire il percorso "Display->Show Tables" e selezionare "Elements Output" per ottenere tutti le caratteristiche geometriche e meccaniche riguardanti le aste.
In particolare tramite le tabelle generate da SAP è possibile definire il valore dello sforzo normale di compressione e di trazione massimo e su quali aste questi valori agiscono. Per ottenere le tabelle è sufficiente seguire il percorso "Display->Show Tables" e selezionare "Elements Output" per ottenere tutti le caratteristiche geometriche e meccaniche riguardanti le aste.