In ritardo ma arrivo...

Per sbaglio ho pubblicato l'esercitazione nei commenti, e non posso modificarlo. Inoltre devo caricare le immagini sul server, per cui non risultano nei commenti.

 

La seguente è l'esercitazione fatta in parallelo coi miei colleghi Vanetti e Pontrandolfi del laboratorio di progettazione 2M.

SOVRACCARICO PERMANENTE

Vorremmo avere nel caso di acciaio e legno un identico tipo di solaio, per cui dopo aver definito la stratigrafia, che segue, abbiamo calcolato il peso proprio per metro quadro del solaio e successivamente i carichi accidentali e permanenti.

 

 

• 15 mm – Parquet

• 40 mm - Isolante con listelli di legno

• 100 mm - Getto collaborante con rete elettrosaldata

• 57 mm – Tavole di Xlam a 5 strati incrociati

 

Per calcolare il peso unitario del solaio è necessario trovare le masse volumiche degli elementi che compongono i singoli strati. Per lo strato "isolante con listelli di legno" è sufficiente fare una media ponderata tra la massa volumica del legno e quella dell'isolante.

 

Masse volumiche:

• • Parquet chiaro : 720 kg/mc

  • Listelli di legno : 500 kg/mc - Isolante : 80 kg/mc

  • Getto collaborante : 1800 kg/mc

  • Rete elettrosaldata : 2.98 kg/mq

  • Xlam : 700 kg/mc

 

Per ottenere il valore unitario a metro quadro è sufficiente moltiplicare la massa volumica per lo spessore, in modo tale da ottenere la massa per ogni metro quadro.

Quindi avremo :

• • Parquet chiaro : 720 * 0.015 = 10.8 kg/mq

  • Listelli di legno : 500 * 0,04 = 20 kg/mq - Isolante : 80 *0.04 = 3.2 kg/mq

Supponendo i listelli ogni metro di pavimento avremo per ogni metro quadrato di pavimento il 96% di isolante e il 4% di listelli, quindi un totale di 20 * 0.04+3.2 * 0,96 = 3.872 kg/mq per l'intero strato.

• • Getto collaborante : 1800 *0.1 = 180 kg/mq

  • Rete elettrosaldata : 2.98 kg/mq

  • Xlam : 700 * 0.057 = 39.9 kg/mq

 

E' sufficiente fare la somma quindi per ottenere il peso del solaio per ogni metro quadrato, quindi:

 

q_p = 10.8 + 3.872 + 180 + 2.98 + 39.9 = 237.552 kg/mq = 2,33 kN/mq

 

Questo è il peso totale del solaio, senza distinzione tra carico permanente strutturale e non strutturale. Non considerandolo come unicum ma diviso tra i due campi, si scomporrebbe nel seguente modo:

Carico permanente strutturale q_s = Xlam + getto collaborante = 222,88 kg/mq = 2.186 kN/mq

Carico perm. non strutturale q_pSolaio =Parquet + isolante + listelli = 14.58 kg/mq= 0.143 kN/mq

Tuttavia è ancora necessario andare a definire l'orditura dei travetti che collegano una trave principale all'altra e che reggono i pannelli in Xlam. L'XLam di 5,7 cm regge bene fino a luci di anche 8 metri, ma vista la destinazione d'uso andiamo a definire una maglia orizzontale di 4 m.

 

ACCIAIO:

Quindi a gravare ulteriormente sul carico permanente della trave principale ci saranno due ulteriori travi perpendicolari ad essa.

 

 

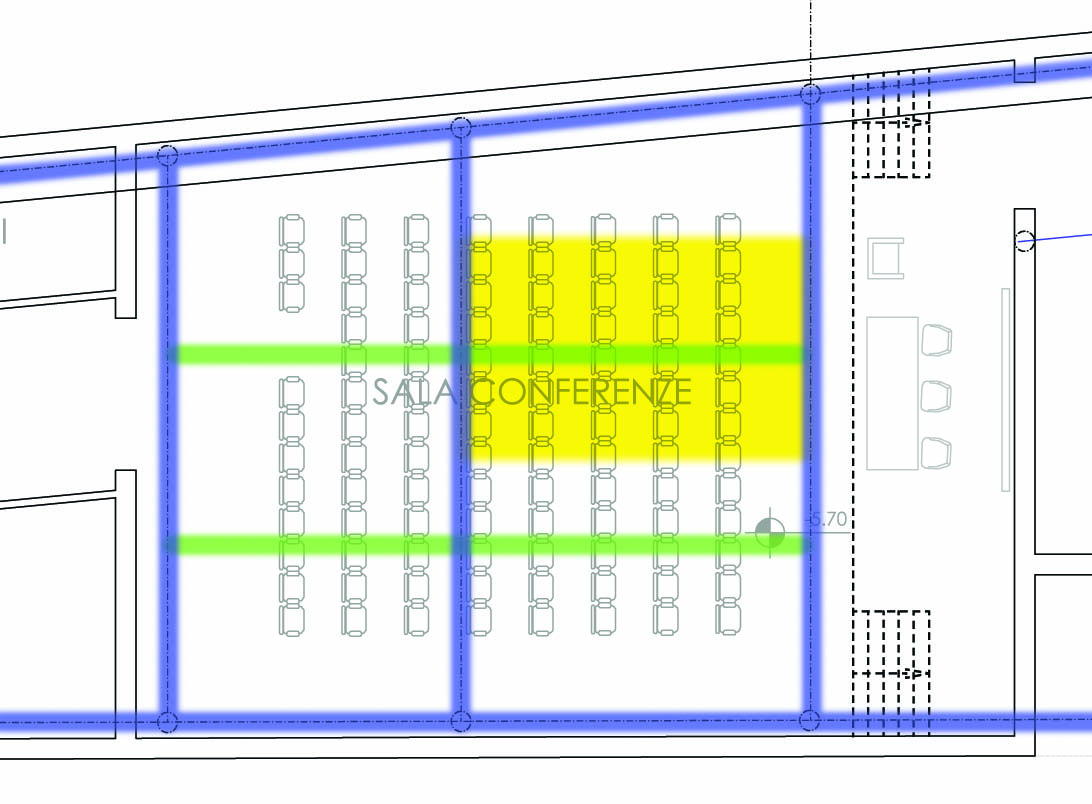
Pensiamo di utilizzare degli scatolati quadrati.

E' corretto come criterio progettuale andare prima a calcolare le dimensioni degli scatolati perpendicolari piuttosto che ipotizzarne un paio generici che pesano sulla nostra trave, anche perchè il peso potrebbe variare notevolmente tra una scelta e l'altra.

Per cui scegliamo l'area di pertinenza più grossa, ovvero quella evidenziata in giallo. La luce sarà di 6.93 m, mentre l'interasse come visto è di 4m. L'area di influenza è quindi 27.72 mq, per un peso totale di 2.33 kN/mq * 27.72 mq = 64.68 kN che gravano sullo scatolato.

 

 

Da questi valori vediamo come sia necessaria una Wx di 787 cm^3 almeno per poter garantire il corretto funzionamento dell'orditura secondaria. Andiamo a cercare tra i vari tipi di trave d'acciaio forniti da Oppo.it.

HEA: 836 cm^3 è il valore superiore più vicino a quello da noi cercato, e corrisponde a una HEA 260, quindi alta 260 mm e larga 250 mm. Pesa 68.2 kg/m

HEB: 938 cm^3 per una HEB 240, larga e alta 240mm. Pesa 83.2 kg/m.

HEM: 967 cm^3 per una HEM200, alta 220mm e larga 206mm. Pesa 103 kg/m.

SCATOLATO QUADRO: 1085 cm^3 per una larghezza/altezza di 300mm e un peso di 91.1 kg/m

Lo scatolato a sezione rettangolare non raggiunge la resistenza da noi richiesta quindi è da escludere. Per vantaggio sia in termini di peso che in termini di dimensioni scegliamo l'HEA.

 

Ora è necessario andare a calcolare tra i carichi permanenti non strutturali il peso incidente dei tramezzi al piano superiore, ma prima bisogna scegliere la trave da analizzare e definire l'area di influenza di essa, in modo poi da porre considerazioni sull'incidenza dei tramezzi soprastanti.

Essendo che andrebbe considerato anche il peso stesso della trave, ma è proprio la cosa da valutare, per ora porremo solamente un tipo di trave come esempio per il calcolo delle sollecitazioni e andremo poi a sostituire in base al valore di Wx la trave adatta.

 

Scegliamo la trave con la campata più problematica, quella che affaccia sulla sala conferenze, con una campata di 11.7 m. L'area di pertinenza è quella che va dalla metà della porzione di solaio alla sua destra e alla sua sinistra, perchè in linea di massima andranno a pesare completamente sulla trave più vicina.

La distanza tra la trave in analisi e quella alla sua sinistra è di 5.81 m, con quella alla sua destra 6.93 m. L'interasse quindi è 5.81/2 + 6.93/2 = 6.37 m. L'area di influenza è di 74.63 mq.

Nel nostro caso abbiamo che al piano superiore non c'è incidenza di tramezzi, per cui non ci sarà un ulteriore carico permanente a gravare sulla trave.

Abbiamo quindi tutti gli elementi necessari per compilare la tabella per avere il valore di Wx necessario a capire quale trave in acciaio scegliere.

E' necessario aggiungere a quanto calcolato precedentemente il peso delle travi HEA perpendicolari. Sapendo che l'area di influenza è la seguente:

 

 

sappiamo che dovremo prendere in considerazione il peso dato da due travi HEA alte 260mm per una lunghezza totale pari alla larghezza dell'area di influenza. Quindi moltiplichiamo il peso lineare di 68.2 kg/m * 6.37m = 434.434 kg. Per avere il valore di peso unitario è sufficiente dividere per l'area di influenza, quindi 434.434/74.63= 5.81 kg/mq = 0.057kN/mq.

Andranno sommati quindi ai 2.186 dei carichi strutturali permanenti, per ottenere qp=2.243 KN/mq

 

Per i carichi variabili dobbiamo considerare l'area come luogo affollato (libreria): Qa=500 Kg/mq

---> Qa=5 KN/mq

 

 

Sostituendo come si vede nell'immagine i valori dell'interasse, dei carichi permanenti non strutturali, strutturali e accidentali, e il valore della luce otteniamo una Wx di 3597 cm^3, valore molto alto.
Abbiamo aggiunto al foglio excel delle pagine contenenti i valori di tutte le tipologie note di travi di acciaio fornite da Oppo.it, ovvero le HEA, HEB, IPE, HEM, in modo da avere un rapido raffronto con il valore ottenuto.

Il nostro Wx = 3597 cm^3 va confrontato con le tipologie sopracitate, e prendere ovviamente un valore superiore nel caso della trave scelta.

IPE : Nel caso di una IPE Wx si ferma a 3069 per una trave alta 600mm, quindi dobbiamo escludere questo tipo di trave.

HEA: Il valore più vicino è 4146 cm^3, per una HEA 550, quindi con h=540mm e b=300mm.

HEB: Il valore più vicino è 4287 cm^3, per una HEB 500, quindi con h=500mm e b=300mm.

HEM: Il valore più vicino è 3796 cm^3, per una HEM 320, quindi con h=359mm e b=309mm.

SCATOLATI: Sia gli scatolati rettangolari che quadrati che i tubolari non arrivano a garantire una resistenza Wx di 3569, quindi è da escludere a priori la categoria.

 

La HEM è quella più vantaggiosa come dimensioni totali, solamente che è la più vicina in assoluto come valore di resistenza a quella ottenuta dal nostro calcolo. Vogliamo avere un minimo di tolleranza in più, anche perchè non abbiamo ancora considerato il peso stesso della trave e l'orditura che regge il solaio. Scegliamo quindi la HEB500, che ha un peso di 270kg/m.

 

Il foglio excel ci è servito per il corretto dimensionamento della trave principale, ma non abbiamo calcolato il peso stesso della trave, che è molto importante. Per cui abbiamo preso l'iniziativa di modificare il file excel e aggiungere tre ulteriori colonne, una contenente il peso lineare della trave scelta, uno con il momento risultante aggiungendo il carico della trave stessa e soprattutto il Wx reale, tenendo conto del carico proprio della trave.

 

 

 

Come vedete il momento aumenta di circa 50 KN*m, ma soprattutto il Wx aumenta di 200 cm^3. Questo aumento potrebbe portare a un cambiamento di scelta per il tipo di trave; noi volutamente abbiamo scelto la trave che ci desse più margine di respiro in vista di un aumento del modulo di resistenza dovuto all'aggiunta del peso proprio, infatti possiamo mantenere la stessa HEB500, che resiste fino a 4287 cm^3!

 

LEGNO:

Essendo il tipo di stratigrafia equivalente per legno e acciaio senza alcun problema ( solamente nel caso del CLS sarà più una forzatura, ma è voluta al fine di effettuare un utile confronto tra le tipologie di travi), il carico permanente sarà lo stesso, eccezion fatta che per l'orditura secondaria. Sicuramente non siamo in grado di garantire all'Xlam una campata di 4 metri su un travetto di legno lungo 6.93 metri, per cui urge andare a ricalcolare il modulo di resistenza per le travi secondarie in legno, ipotizzando una maglia magari di 3 metri anzichè 4.

 

 

In questo caso quindi saranno uguali tutti i valori da applicare, carichi compresi, ma cambierà l'interasse, che in questo caso è di 3m.

 

 

Scegliamo quello di classe di resistenza GL36, il più resistente alla trazione generata dalla flessione. Kmod vale 0,5, perchè è un carico permanente, di classe di servizio 3. Come base ci imponiamo 30cm, e l'altezza risultante è di 46.11 cm.

 

 

Una volta definite le dimensioni dell'orditura secondaria è possibile calcolare il carico da aggiungere alla trave principale lungo la sua area di influenza, e sarà l'area della sezione della trave appena trovata moltiplicata per la larghezza dell'area di influenza per quattro volte.

Peso travi = 0,46*0,3*6,93*500 4* = 1738,4 kg = 17,38 KN.

Dobbiamo ottenere il peso unitario per mq di queste travi, che saranno quindi 17,38/74,63= 0,23 KN/mq.

Quindi andiamo ad aggiungere il carico dovuto alla presenza di travi secondarie al carico permanente, per ottenere il dimensionamento della trave principale.

 

 

Come si vede dal foglio excel, imponendo una base di 50 cm la risultante è un'altezza di 93,1 cm. Ora come nel caso precedente sarebbe possibile calcolare il momento massimo tenendo conto del peso proprio della trave, che ora è noto.

 

 

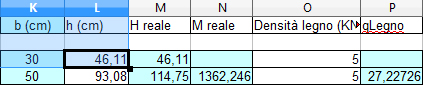
In questo caso abbiamo nuovamente aggiunto al calcolo 4 colonne, per l'inserimento della massa volumica del tipo di legno scelto, poi per il peso totale della trave, per il momento generato aggiungendo questo carico e infine l'altezza risultante aggiungento il carico proprio della trave principale. In questo caso è notevole la differenza, infatti a parità di base l'altezza passa da 93 a 115 cm, ovvero 22 cm più alta!

 

 

CLS:

 

Il seguente caso è quello che ha richiesto una "forzatura" nella concezione della nostra analisi dimensionale, perchè il tipo di solaio in esame non è solitamente utilizzato associato a una struttura in cemento armato; noi vogliamo mantenerlo anche sulla struttura in CLS per evidenziarne il differente comportamento a fronte di pari sollecitazioni. Inoltre il tipo di solaio solitamente associabile a una struttura in CLS è più pesante di quello in questione, per cui gli output relativi all'altezza della trave saranno persino maggiori nella realtà di quelli uscenti dal foglio di calcolo.

Non abbiamo travi secondarie a gravare sul peso stesso della trave, ma dobbiamo infittire la maglia dei pilastri, per garantire al solaio una luce fattibile in termini di resistenza.

 

 

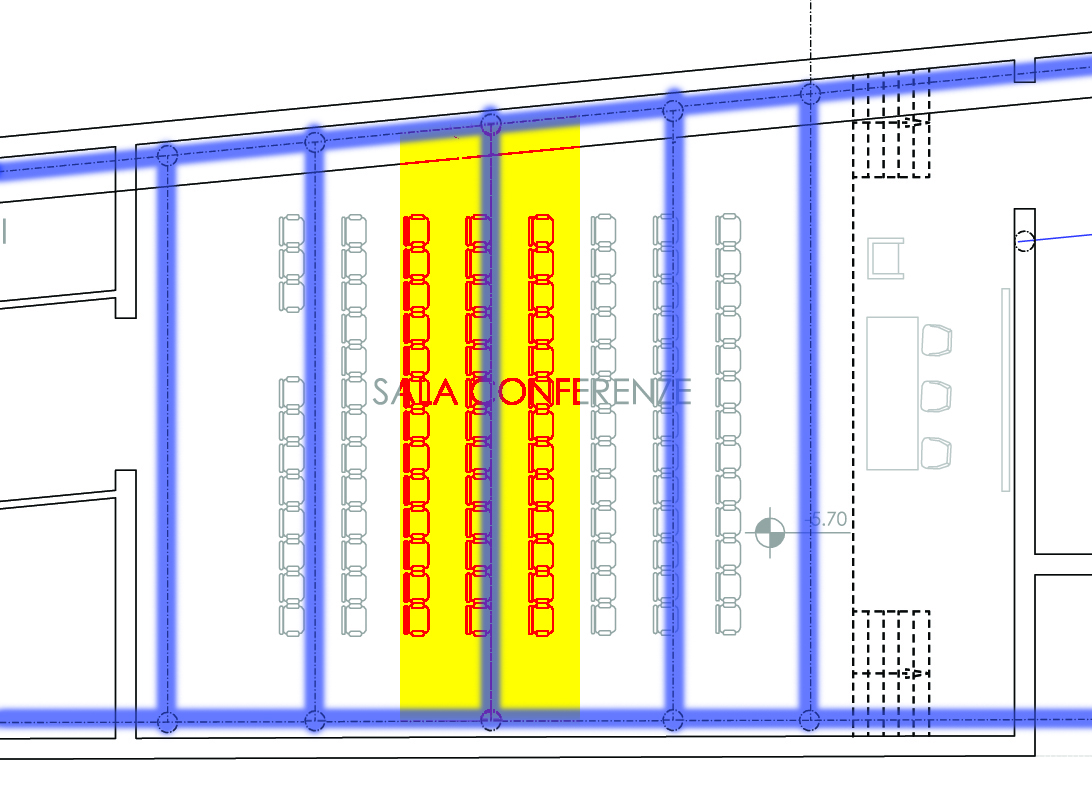
In questo caso abbiamo un interasse di 3.5 m, con la stessa luce di 11.7 m. E' sufficiente calcolare l'altezza della trave senza aggiungere carichi aggiuntivi oltre a quello della trave stessa, ma solo in un secondo momento.

Tra gli input immettiamo gli stessi carichi, scegliamo un acciaio S235JR, con una tensione di snervamento di 235 N/mm² = fy. Classe di resistenza Rck = 40. Ci poniamo una larghezza desiderata per la trave di 40 cm, e un copriferro di 3 cm.

 

 

 

Il dato uscente è un'altezza di 46,12 cm al netto del ferro. Tuttavia manca il peso proprio della trave nel calcolo per il dimensionamento, per cui abbiamo aggiunto quattro colonne al foglio di calcolo, che vanno a modificare il carico permanente, il momento e di conseguenza l'altezza della trave.

 

 

Come si può vedere l'altezza finale risulta di 49,32 cm, a cui dobbiamo aggiungere 3 cm di copriferro, per l'ingombro totale, ovvero H = 52,32 cm. E' un valore dissimile da quello che la pratica insegna per luci superiori ai 10m, per cui dovremmo avere all'incirca una trave spessa 100 cm. Probabilmente il fattore solaio leggero incide notevolmente sul calcolo finale, oltre che il piccolo interasse che gli abbiamo concesso.

 

 

 

PER COSTRUIRE UN MODELLO DI STRUTTURA RETICOLARE NELLO SPAZIO 3D:

 

 

strumenti: autoCAD 3D; SAP2000

 

 

 

 

Il primo passo da fare è aprire autoCAD e creare un layer dove andremo a disegnare, tramite il comando linea, il modulo di partenza da cui andremo a creare la nostra struttura.

Passiamo poi alla vista in 3D:

  view > 3D view > scegliamo una delle viste assonometriche (preferendo l'asse z vesto l'alto)

Poi andiamo a ruotare il nostro modulo di base:

  3r > invio > seleziono l'elemento > quando compaiono gli assi di rotazione scelgo prima il punto e successivamente l'asse di rotazione

Utilizziamo il modulo di base per completare la struttura reticolare, per far ciò possiamo utilizzare o il comando array o più semplicemente il comando copia.

Salviamo il nostro file in formato .dxf 2000.

Apriamo SAP 2000 e importiamo il nostro file:

  file > import > autoCAD dxf file > frame > aste > ok

Impostiamo ora i vincoli di base, ovvero andiamo a posizionare delle cerniere nei 4 vertici della struttura.

Selezioniamo tutto e procediamo con l'imposizione delle cerniere interne nei nodi della trave reticolare:

  assign > frame relese > moment(2-2) e (3-3) spuntiamoli ed assegnamo il valore 0 sia all'inizio che alla fine

Fondamentale è la definizione del materiale e della sezione, andiamo quindi su define:

  define > section propieties > frame prop. > ne scegliamo una > add new

  assign > frame > frame section

Andiamo ad assegnare il nostro carico sui nodi superiori della nostra struttura, per far ciò andiamo su display option e nascondiamo le nostre aste.

  define > load pattern > forza concentrata

  Assign > joint loads > forces > carico concentrato > lungo z da -40kN

Andiamo a far riapparire le nostre aste (display option).

Ora non ci resta che avviare il RUN ricordandoci di deselezionare i carichi DEAD e MODAL.

Osserviamo i valori degli sforzi normali, e per verificare che la struttura sia corretta proviamo a vedere i grafici dei tagli e dei momenti, i quali dovranno risultare nulli.

(ho problemi col server, non mi si apre e non riesco dunque a caricare le immagini)