ESERCITAZIONI PROGETTAZIONE STRUTTURALE B

TRAVATURE RETICOLARI SIMMETRICHE E ASIMMETRICHE

Queste prime esercitazioni vertono sulla risoluzione delle travature reticolari isostatiche, simmetriche e asimmetriche, tramite l’applicazione di due diversi metodi di calcolo: il metodo delle sezioni di Ritter, attraverso il quale si eseguono dei tagli virtuali che permettono di calcolare le azioni di contatto delle aste, e il metodo dei nodi, che vede l’isolamento dei vari nodi della struttura e la scrittura delle equazioni di equilibrio relative al nodo in esame. Nel caso delle travature reticolari soggette a carichi concentrati, le sole azioni di contatto sono riconducibili allo sforzo normale (trazione e compressione), giacché taglio e momento risultano essere nulli. Pertanto si dovrà verificare se le aste della trave (correnti o diagonali), collegate tra loro tramite cerniere (nodi), sono tese o viceversa compresse. Verranno quindi denominate, a seconda della sollecitazione agente, tiranti o puntoni.

Viene inizialmente assegnata una struttura reticolare simmetrica sia per struttura che per forze esterne applicate. Difatti in corrispondenza dei nodi B, P e G agiscono dei carichi concentrati di valore 20 KN, in direzione della forza gravitazionale. Prima di procedere al calcolo delle azioni di contatto è necessario verificare la condizione di isostaticità della trave, possibile attraverso l’applicazione di due metodi, e procedere quindi al calcolo delle reazioni vincolari: 

Risolviamo la struttura tramite il metodo di Ritter: si opera una sezione ideale che divide la trave integralmente in due parti sezionando solo tre aste non concorrenti nello stesso punto. Si disegna lo schema isolando una delle due porzioni e si calcolano gli sforzi assiali mediante l’equazione di equilibrio dei momenti intorno al polo di riferimento. Per le aste diagonali bisogna scomporre il vettore dello sforzo assiale nelle sue componenti orizzontale e verticale, ma poiché l’angolo risulta essere di 45° esse avranno valore uguale e pari al modulo dello sforzo normale moltiplicato per sqrt(2)/2. A seconda dei valori (positivo o negativo), si verificherà se le aste sono tese o compresse e se i versi ipotizzati a priori erano esatti o da invertire: 

 

Poiché la struttura è simmetrica, i calcoli possono essere effettuati solo per metà trave ed estesi all’altra metà.

 

La seconda struttura reticolare non risulta essere simmetrica. Per calcolare le azioni di contatto viene usato il metodo dei nodi. 

 

Il primo passaggio prevede sempre la verifica dell’isostaticità della trave e il successivo calcolo delle reazioni vincolari dei nodi B e G. 

 

Viene individuato il nodo più conveniente (o semplice) da analizzare per procedere in successione all’analisi dei restanti nodi. In questo caso è opportuno partire dall’analisi dal nodo G, giacché presenta due sole incognite e il valore definito della reazione orizzontale del carrello, precedentemente calcolato. Si procede isolando il nodo, esplicitando gli sforzi assiali sulle aste e risolvendo le equazioni di equilibrio. Poiché le forze sono convergenti al nodo, l’equazione di equilibrio dei momenti rispetto al nodo stesso è identicamente soddisfatta (ΣMnodo=0). Nel caso piano si hanno pertanto a disposizione perogni nodo solo le rimanenti due equazioni di equilibrio: ΣFx,nodo=0 e ΣFy,nodo=0.

 

La struttura viene verificata con il software di calcolo strutturale SAP 2000.

1) Viene creato un nuovo modello partendo dalla griglia:

GRID LINES: x=4, y=1, z=2

GRID SPACING: x=1, y=1, z=1      non consideriamo il valore y poiché siamo nel piano 2D x,z

2) Attraverso lo strumento linea viene disegnata la struttura, dove le aste risultano essere ancora unite. 

 

3) Si assegnano i vincoli ai punti B e G: si seleziona il punto di riferimento -> ASSIGN -> JOINT  
   ->RESTRAITS:

per il punto B si assegna la cerniera di default, per il punto C il carrello la cui traslazione avviene lungo l’asse x (1).

4) Si definiscono le forze concentrate: DEFINE -> LOAD PATTERNS -> si crea una nuova forza con il fattore di moltiplicazione pari a zero.

Sempre DEFINE -> LOAD CASES -> Si eliminano DEAD, MODEL (delete load cases).

Cliccando sui nodi interessati dalle forze, gli si assegnano i carichi: ASSIGN -> JOINT FRAME
 ->FORCES: si assegna la forza prima definita:

-       FORCE GLOBAL Z: -10 KN            

      si mette il valore negativo per indicare una forza gravitazionale verso il basso 

5) Bisogna dare un’ulteriore indicazione riguardante le aste, poiché SAP considera i nodi tra le aste come incastri interni, mentre fra le aste vi è un vincolo di cerniera interna. Pertanto si seleziona la struttura -> ASSIGN -> FRAME -> RELEASES/PARTIAL FIXITY:

- MOMENT 33: si spunta sia start che end (momento nullo sia all’inizio che alla fine). 

6) A questo punto di può avviare l’analisi ed esaminare la deformata, il diagramma delle sollecitazioni e visualizzare la tabella dei valori: 

 

DIMENSIONAMENTO TRAVI TRAMITE IL FOGLIO DI CALCOLO EXCEL

 

Per l’esercitazione riguardante il dimensionamento delle travi tramite il foglio elettronico excel, considero l’impalcato ipotizzato per gli alloggi di un albergo, il cui programma funzionale è stato fornito dal corso di “Laboratorio di Progettazione 2M”, eseguito in collaborazione con Emanuel Dad Khan e Sara Forlani. 
   

 

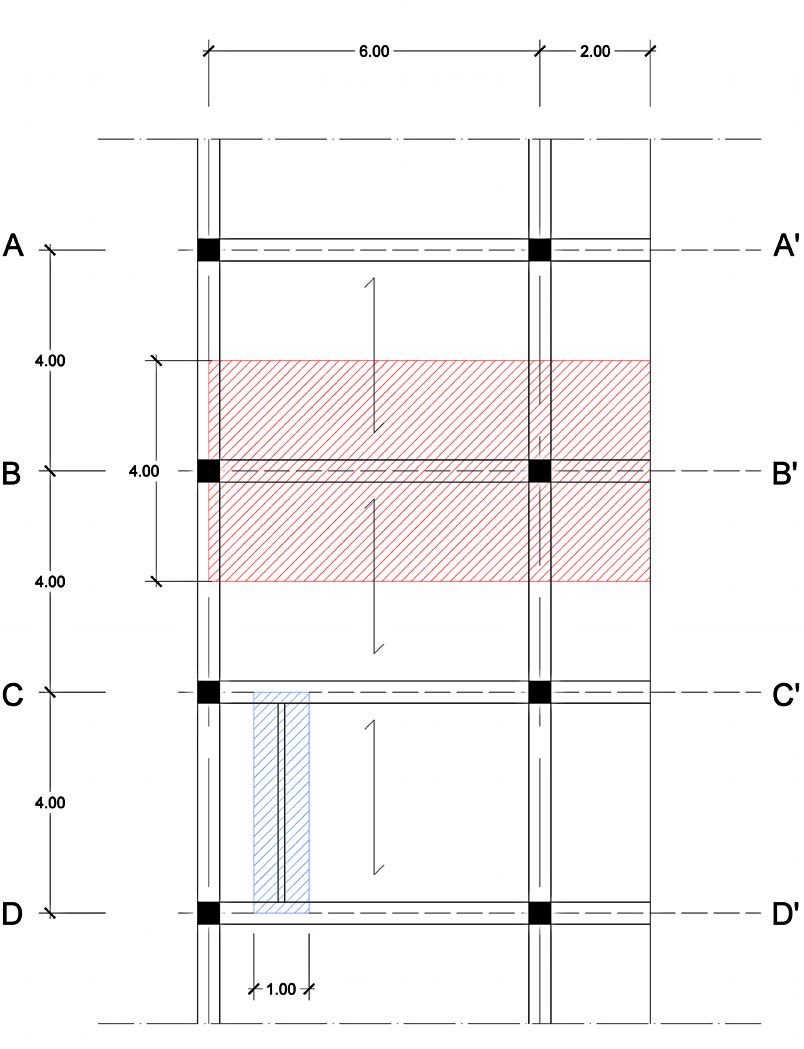
Dopo aver disegnato il telaio strutturale, costituito da travi a sbalzo e pilastri, considero la trave maggiormente sollecitata da sottoporre all’analisi. Prendo quindi in esame la trave relativa all’interasse B-B’, la cui area di influenza è pari a:

A_trave= interasse x luce, ovvero
32,00 mq= 8,00 m x 4,00 m .

Il dimensionamento sarà effettuato in base alle tabelle riguardanti i tre materiali presi in esame nel corso: legno, acciaio e cemento armato.
Per tutti e tre i materiali, progetto e verifico innanzitutto il travetto della struttura e in seguito procedo alla progettazione e verifica della trave. L’area di influenza del travetto risulta essere:

per legno e acciaio:

A_travetto= interasse x luce
4,00 mq= 1,00 m x 4,00 m

per calcestruzzo:

A_travetto= interasse x luce
2,00 mq= 0,50 m x 4,00 m

Devo inoltre considerare a quali carichi la struttura verrà sottoposta, ovvero a quali azioni la costruzione dovrà resistere.
“Si definisce azione ogni causa o insieme di cause capace di indurre uno stato limite in una struttura”⁽¹⁾. Queste azioni vengono classificate dalla normativa vigente in base alla variazione della loro intensità nel tempo e si distinguono in:

·      Permanenti: ovvero quelle azioni la cui durata è strettamente vincolata alla vita nominale della costruzione e la cui variazione è approssimativamente considerata costante nel tempo.  Vengono considerati sotto questa voce, ad esempio, il peso proprio degli elementi strutturali (azioni permanenti strutturali) e quello degli elementi non strutturali (permanenti portati).

·      Variabili: ovvero i carichi definiti come accidentali. Sono quei sovraccarichi legati alla destinazione d’uso degli edifci/locali, o le azioni dovute agli agenti atmosferici (vento, neve).

·      Eccezionali: azioni che si verificano eccezionalmente, come ad esempio incendi ed esplosioni.

·      Sismiche: azioni derivanti dai terremoti.

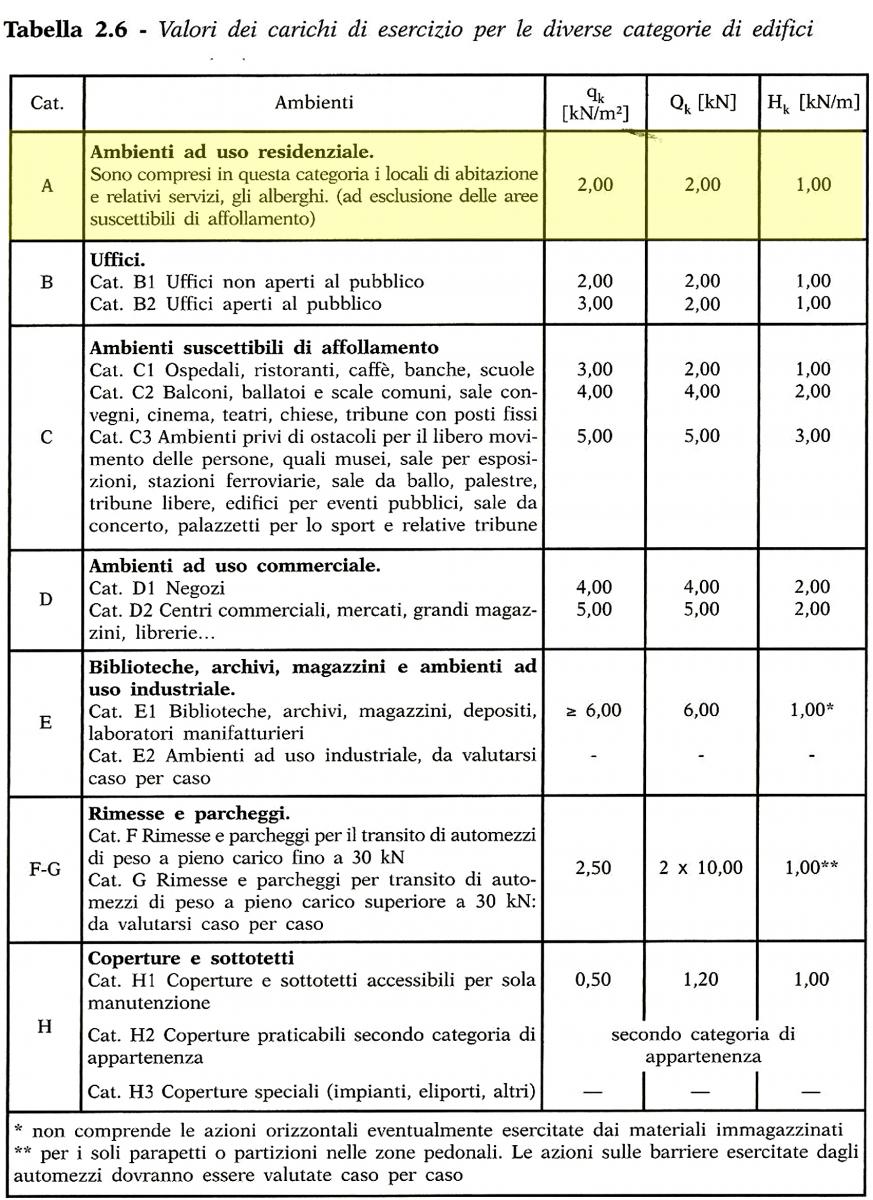
Per i valori dei carichi di esercizio, riporto la tabella 2.6 tratta dal libro:
Boscolo Bielo, M. “Progettazione strutturale, significato e prassi della nuova normativa antisisimic”, Legislazione Tecnica, 2010, Roma. 

 

 

SOLAIO IN LEGNO:

 

Riferimento per la soluzione strutturale tratta da:
Benedetti, C.- Bacigalupi, V. “Materiali e progetto”, Edizioni Kappa, 2005, Roma.

TRAVETTI:

Carichi strutturali (qs)

• Impalcato in legno di noce:                                                                                                                   peso specifico : 600 kg/mc (per legno stagionato)                                                                         volume tavolato (per 1 mq) : 0,05 m x 1,00 m x 1 ,00 m = 0,05 mc                                               peso tavolato (per 1 mq) : 600 kg/mc x 0,05 mc = 30 kg/mq = 0,30 kN/m

Sovraccarichi permanenti (permanenti portati, qp)     

• Massetto in cemento :                                                                                                                          massa volumica : 2000 kg/mc                                                                                                        volume massetto (per 1 mq) : 0,07 m x 1,00 m x 1 ,00 m = 0,07 mc                                            peso massetto (per 1 mq) : 2000 kg/mc x 0,07 mc = 140 kg/mq = 1,40 kN/mq 
• Isolante acustico : del tipo PIOMBOROLL DUO 0,60                                                                                peso isolante (per 1 mq) : 7 kg/mq = 0,07 kN/mq

   

• Parquet in rovere:                                                                                                                                  peso specifico : 750 kg/mc                                                                                                           volume parquet (per 1 mq) : 0,02 m x 1,00 m x 1 ,00 m = 0,02 mc                                               peso parquet (per 1 mq) : 750 kg/mc x 0,02 mc = 15 kg/mq = 0,15 kN/mq
• Incidenza impianti: 0,5 kN/mq
• Incidenza tramezzi: 1 kN/mq

Sovraccarichi accidentali (qa)

• Ambienti ad uso residenziale : 2 kN/mq

CARICO TOTALE : (qs+qp+qa) x interasse
(0,30 + 3,12 + 2) x 1 = 5,42 kN/m

Calcolo il momento massimo per una trave appoggiata-appoggiata soggetta a un carico distribuito pari a 5,42 kN/m, tramite la formula: q*l^2/8.
Inserisco quindi i dati trovati (relativi ai carichi e al momento massimo) nella tabella excel riguardante il legno, scegliendo una classe di resistenza del materiale pari a GL24H,con fm,k=24 N/mmq e un valore di 0,7 (per legno lamellare) per il coefficiente kmod (durata del materiale).  Infine inserisco un valore ipotetico per la base della sezione del travetto pari a 12,00 cm, trovando così un’altezza di 21,63 cm.
Tramite un profilario, fornito dall’azienda produttrice di legno lamellare Kaufman-Canducci, scelgo quindi una sezione dalle dimensioni di 12 cm x 22 cm.

Procedo quindi alla verifica, aggiungendo al valore in precedenza calcolato dei carichi strutturali il valore riguardante il peso del travetto:

• Travetto in legno lamellare:                                                                                                                    peso specifico : 450 kg/mc      
          volume travetto (per 1 mq) : 0,12 m x 0,22 m x 1 ,00 m = 0,0264 mc                                           peso travetto (per 1 mq) : 450 kg/mc x 0,0264 mc = 11,88 kg/mq = 0,12 kN/mq

CARICO TOTALE:(qs+qp+qa) x interasse
(0,42 + 3,12 + 2) x 1 = 5,54 kN/m

Inserendo questo nuovo valore nella stessa tabella excel, trovo una sezione la cui altezza è pari a 21,87 cm < 22 cm, LA SEZIONE E’ PERTANTO VERIFICATA.

TRAVE:
Considero ora la trave, il cui interasse è di 4,00 m:

CARICO TOTALE:(qs+qp+qa) x interasse
(0,42 + 3,12 + 2) x 4 = 22,16 kN/m

Prima di inserire i nuovi dati nella tabella excel, calcolo il momento massimo cui è soggetta la trave appoggiata-appoggiata con sbalzo. Utilizzo quindi il programma di calcolo SAP 2000 e riporto il diagramma del momento:
Inseriti i valori, scelgo una classe di resistenza del legno pari a GL36H e ipotizzo un valore per la base della sezione pari a 20 cm, ottenendo un valore di altezza di 36,81 cm. Scelgo pertanto da profilario una sezione di 20 x 40 cm. 

Procedo quindi alla verifica, aggiungendo al valore in precedenza calcolato dei carichi strutturali, il valore concernente il peso della trave:

• Trave in legno lamellare:
          peso specifico : 450 kg/mc                                                                                
          volume trave : 0,20 m x 0,40 m x 8,00 m = 0,64 mc                                                                     peso trave : 450 kg/mc x 0,64 mc = 288 kg
          peso distribuito sulla trave : 288 / (8 x 4) = 9 kg/mq = 0,09 kN/mq

CARICO TOTALE:(qs+qp+qa) x interasse
(0,51 + 3,12 + 2) x 4 = 22,52 kN/m

Ricalcolo il momento massimo agente sulla trave con il software di calcolo SAP 2000, inserendo il carico trovato:

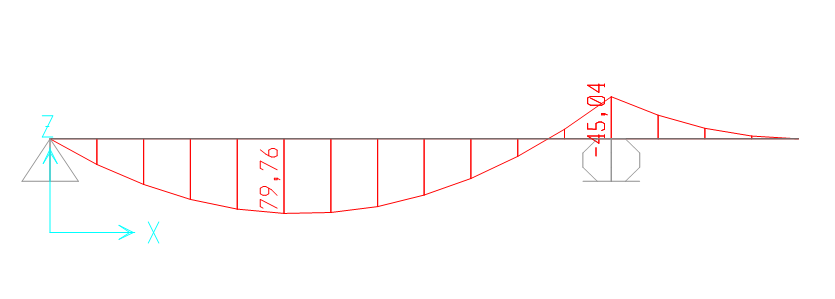
Inserisco i valori nella tabella excel, trovando una sezione la cui altezza è pari a 37,11 cm < 40,00 cm, LA SEZIONE E’ VERIFICATA. 

SOLAIO IN ACCIAIO:
Procediamo analogamente per il dimensionamento della trave di acciaio e del relativo travetto.  

 

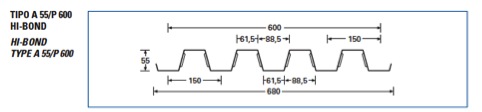
TRAVETTI:

Carichi strutturali (qs)

• Lamiera grecata del tipo A 55/ P 600 HI-BOND, spessore 8 mm:                                                           peso lamiera : 10,47 kg/mq = 0,105 kN/mq    
• Soletta, spessore 12 mm:                                                                                                                       peso soletta : 240 kg/mq = 2,4 kN/mq  

Sovraccarichi permanenti (permanenti portati, qp)

• Getto in calcestruzzo:                                                                                                                            massa volumica : 2000 kg/mc                                                                                                       volume massetto (per 1 mq) : 0,07 m x 1,00 m x 1 ,00 m = 0,07 mc                                             peso massetto (per 1 mq) : 2000 kg/mc x 0,07 mc = 140 kg/mq = 1,40 kN/mq   
• Isolante acustico : del tipo PIOMBOROLL DUO 0,60                                                                                 peso isolante (per 1 mq) : 7 kg/mq = 0,07 kN/mq  
• Pavimento : 0,4 kN/mq
• Controsoffitto in fibra minerale : 0,06 kN/mq
• Incidenza impianti: 0,5 kN/mq
• Incidenza tramezzi: 1 kN/mq

Sovraccarichi accidentali (qa)

• Ambienti ad uso residenziale : 2 kN/mq                                                                                                             

CARICO TOTALE: (qs+qp+qa) x interasse
(2,505 + 3,43 + 2) x 1 = 7,935kN/m ≈7,94 kN/m

Calcolo il momento massimo per una trave appoggiata-appoggiata soggetta a un carico distribuito pari a 7,94 kN/m, tramite la formula: q*l^2/8.
Inserisco quindi i dati trovati (relativi ai carichi e al momento massimo) nella tabella excel relativa all’acciaio, scegliendo una classe di resistenza del ferro pari a FE430S275,trovando così un Wx di 60,59 cm³. 

Tramite il profilario delle IPE scelgo un valore di Wx che meglio approssima per eccesso il valore calcolato. Scelgo pertanto una sezione IPE 140 con Wx = 77,3 cm³.

 

Procedo quindi alla verifica, aggiungendo al valore dei carichi strutturali il valore riguardante il peso del travetto:

• Travetto IPE 140 :                                                                                                                
         peso travetto (per una IPE 140) : 12,9 kg/m                                                                                  peso travetto (per 1 mq) : 12,9/1 = 12,9 kg/mq = 0,13 kN/mq

CARICO TOTALE:(qs+qp+qa) x interasse
(2,635 + 3,43 + 2) x 1 = 8,065 kN/m

Inserendo questo nuovo valore nella stessa tabella excel, viene calcolata una sezione il cui modulo di resistenza Wx = 61,59 cm³ < 77,3 cm³, LA SEZIONE E’ PERTANTO VERIFICATA.

TRAVE:

CARICO TOTALE:(qs+qp+qa) x interasse
(2,635 + 3,43 + 2) x 4 = 32,26 kN/m

Calcolo il momento massimo cui è soggetta la trave appoggiata-appoggiata con sbalzo. Utilizzo  nuovamente il programma di calcolo SAP 2000 e riporto il diagramma del momento:

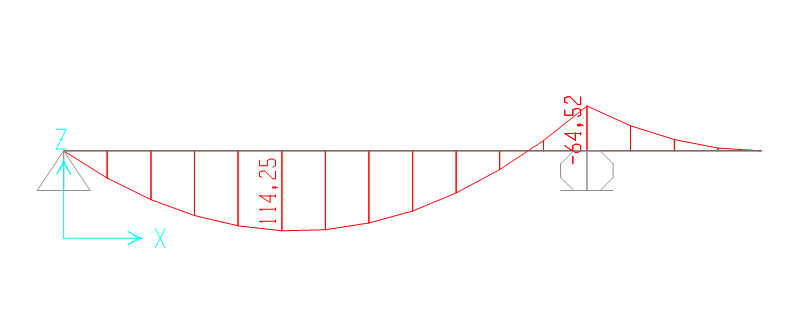
Inseriti i valori, scelgo una classe di resistenza dell’acciaio pari a FE430S275, ottengo una sezione il cui modulo di resistenza è Wx = 436,23 cm^3..

Scelgo quindi una sezione IPE 300, il cui modulo di resistenza vale Wx = 557 cm³.

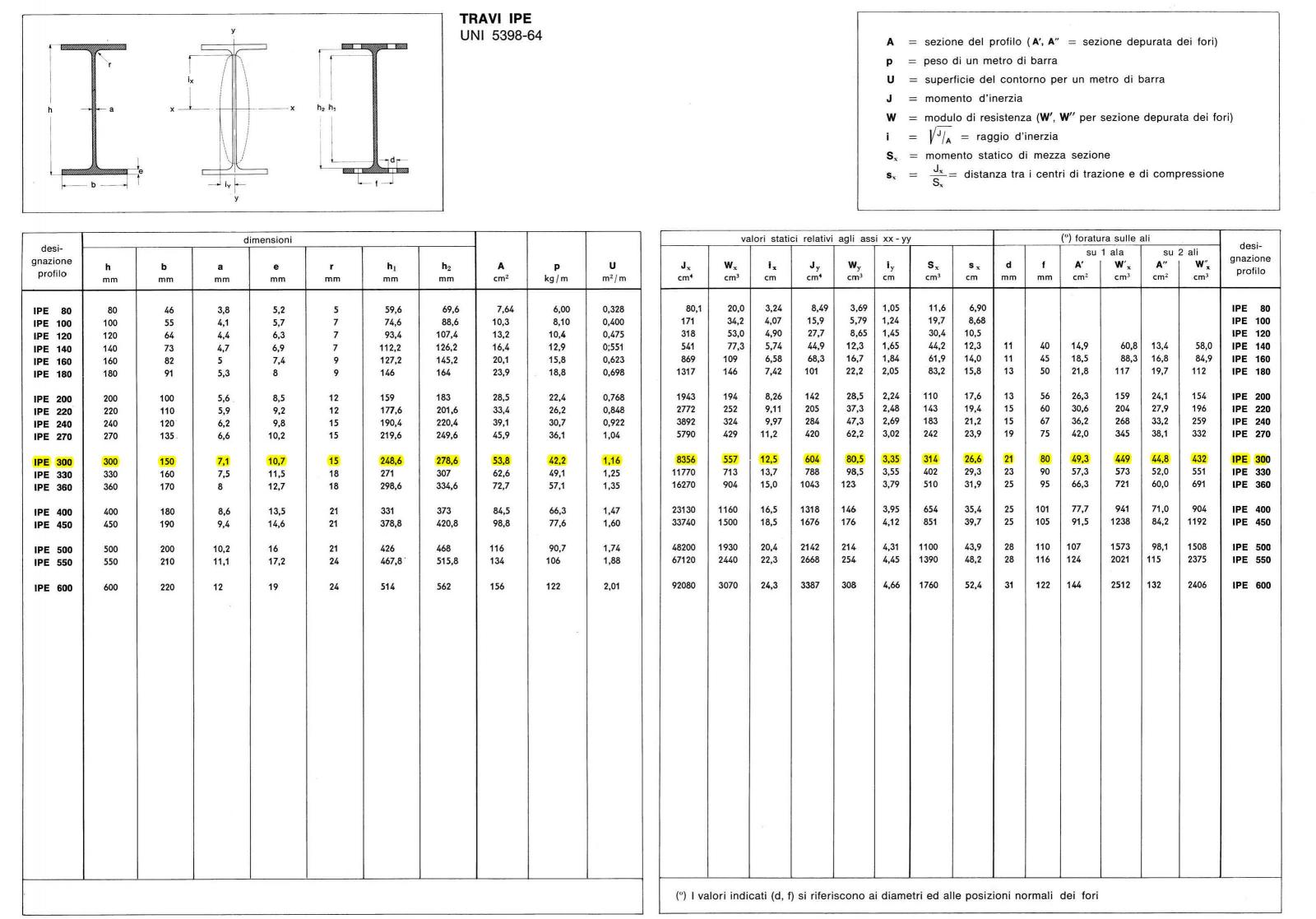
Procedo quindi alla verifica, aggiungendo al valore in precedenza calcolato dei carichi strutturali il valore del peso della trave:

• Trave IPE 300:
         peso trave (per una IPE 300) : 42,2 kg/m                                                                                      peso travetto (per 1 mq) : 42,2/4 = 10,55 kg/mq = 0,1 kN/mq

CARICO TOTALE:(qs+qp+qa) x interasse
(2,735 + 3,43 + 2) x 4 = 32,66 kN/m

Ricalcolo il momento massimo con SAP 2000:

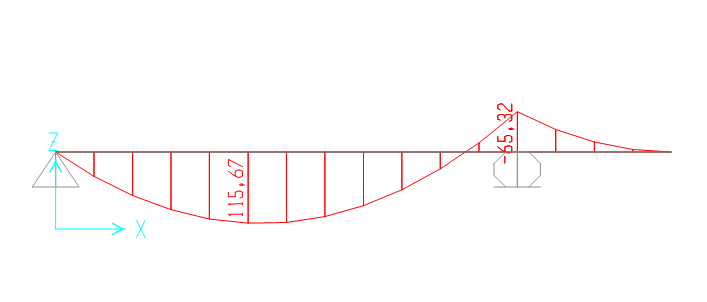
Inserisco i dati nel foglio excel:

Ottengo una sezione il cui modulo di resistenza è pari a Wx = 441,65 cm³ < 557 cm³, LA SEZIONE E’ VERIFICATA. 

SOLAIO IN CLS:
Concludo l’intervento dimensionando la struttura in cemento armato. Considero una soluzione strutturale in latero-cemento:  

 
TRAVETTI:

Considero Carichi strutturali (qs)=0

Sovraccarichi permanenti (permanenti portati, qp)

• Getto in calcestruzzo:                                                                                                                            massa volumica : 2000 kg/mc                                                                                                       volume massetto (per 1 mq) : 0,07 m x 1,00 m x 1 ,00 m = 0,07 mc                                             peso massetto (per 1 mq) : 2000 kg/mc x 0,07 mc = 140 kg/mq = 1,40 kN/mq   
• Isolante acustico : del tipo PIOMBOROLL DUO 0,60                                                                                 peso isolante (per 1 mq) : 7 kg/mq = 0,07 kN/mq  
• Sottofondo in malta:
          peso specifico : 1900 kg/mc                                                                                                         volume sottofondo (per 1 mq) : 0,06 m x 1,00 m x 1 ,00 m = 0,06 mc                                         peso sottofondo (per 1 mq) : 1900 kg/mc x 0,06 mc = 114 kg/mq = 1,14 kN/mq   
• Parquet in rovere : 
          peso specifico : 750 kg/mc                                                                                                           volume parquet (per 1 mq) : 0,02 m x 1,00 m x 1 ,00 m = 0,02 mc                                               peso parquet (per 1 mq) : 750 kg/mc x 0,02 mc = 15 kg/mq = 0,15 kN/mq   
• Intonaco : 
          peso al mq per cm di spessore : 16 kg/mq = 0,16 kN/mq 
• Incidenza impianti: 0,5 kN/mq
• Incidenza tramezzi: 1 kN/mq

Sovraccarichi accidentali (qa)

• Ambienti ad uso residenziale : 2 kN/mq                                                                                                             

CARICO TOTALE: (qs+qp+qa) x interasse
(0 + 4,42 + 2) x0,5 = 3,21 kN/m

Calcolo il momento massimo per una trave appoggiata-appoggiata soggetta ad un carico distribuito pari a 3,21 kN/m, tramite la formula: q*l^2/8. Inserisco quindi i dati trovati (relativi ai carichi e al momento massimo) nella tabella excel riguardante il cemento armato, scegliendo una classe di resistenza del ferro pari a FE360S235 e una classe del cemento C32/40. Scelgo come dimensione della base del travetto 12 cm ottenendo un valore di altezza minima pari a h=9,72 cm e copriferro di 5 cm.

Tramite valori forniti da una ditta trovata in rete, scelgo un pacchetto di solaio in calcestruzzo con interasse 50 cm, travetti da 12 cm di larghezza e altezza 17 cm (12cm + 5cm).

Procedo quindi alla verifica:                                                                                                  

• Solaio in opera (peso tabellato):                                                                                             ·              peso solaio  : 2,48 kN/mq

   

CARICO TOTALE:(qs+qp+qa) x interasse
(2,48 + 4,42 + 2) x0,5 = 4,45 kN/m

Inserendo questo nuovo valore nella stessa tabella excel, calcolo una sezione la cui altezza è pari a 16,44 cm < 17 cm, LA SEZIONE E’ PERTANTO VERIFICATA.

TRAVE:

Il procedimento risulta essere analogo, con l’unica differenza che l’interasse della trave è pari a 4,00 m:

CARICO TOTALE:(qs+qp+qa) x interasse
(2,48 + 4,42 + 2) x 4 = 35,60 kN/m

Prima di inserire i nuovi dati nella tabella excel, bisogna procedere al calcolo del momento massimo a cui è soggetta la trave appoggiata-appoggiata con sbalzo. Utilizzo quindi il programma di calcolo SAP 2000 e riporto il diagramma del momento:

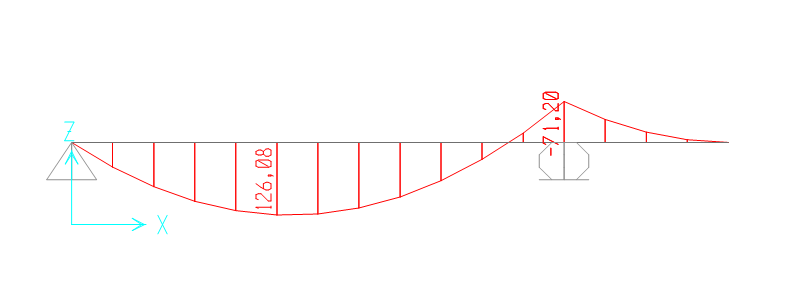
Inseriti i valori, scelgo una classe di resistenza del ferro pari a FE360S235 e del cemento C32/40. Ipotizzo un valore per la base della sezione pari a 20 cm, ottenendo un valore di altezza di 38,36 cm, con 5 cm di copriferro. Scelgo pertanto una sezione di 20 x 40 cm.

Procedo quindi alla verifica, aggiungendo al valore precedentemente calcolato dei carichi strutturali il valore relativo al peso della trave:

• Trave IPE 300:
         peso specifico cemento : 2500 kg/mc                                                                                            volume trave : 0,20 m x 0,40 m x 8,00 m = 0,64 mc
         peso trave : (2500 kg/mc x 0,64 mc)/32 = 50 kg/mq = 0,5 kN/mq                                                                

CARICO TOTALE:(qs+qp+qa) x interasse
(2,98 + 4,42 + 2) x 4 = 37,60 kN/m

Attraverso il software di calcolo SAP 2000 mi calcolo nuovamente il momento massimo:

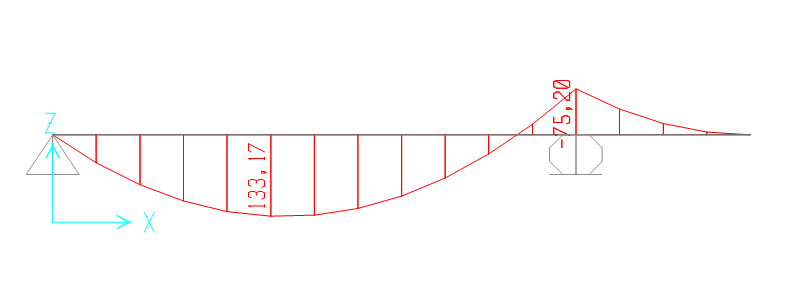
Inserisco i valori nel foglio elettronico excel, trovando un’altezza di 39,28 cm < 40 cm, LA SEZIONE E’ PERTANTO VERIFICATA.

STRUTTURA RETICOLARE IN 3D
DISEGNO DELLA STRUTTURA ATTRAVERSO IL SOFTWARE AUTOCAD 2011:

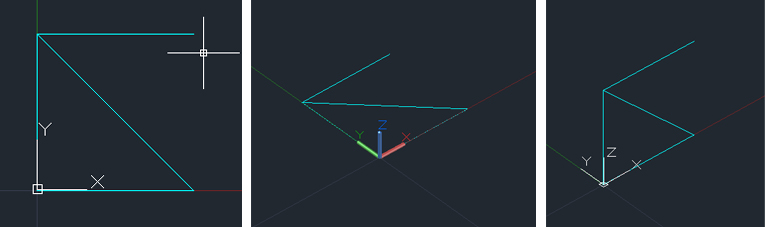
Disegno il modello in AUTOCAD, creando un nuovo layer: “aste”. Per la costruzione tridimensionale della struttura reticolare imposto il modulo base del quadrato con relativa asta diagonale, lasciando accuratamente libero un estremo per permettere la copiatura senza avere ripetizioni di linee e stabilendo che uno dei vertici coincida con l’origine del sistema di riferimento ortogonale: pline ; specify start point: 0,0,0

 

Procedo impostando la vista assonometrica che mi consente di lavorare in tre dimensioni. In seguito ruoto il sistema di riferimento: Modify ; 3D operation ; 3D rotate: angolo 90°

 

Attraverso lo strumento Modify ; 3D operation ; 3D Array replico il modulo base, inserisco quindi:
righe: 1; colonne: 5; distanza tra le colonne: 2
A questo punto posso replicare la struttura in profondità usando sempre il comando serie e impostando:
righe: 7; distanza tra le righe: 2

 

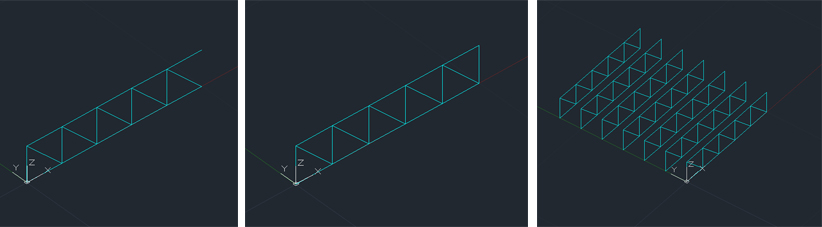
Completo la struttura attraverso lo strumento Polilinea 3D, disegno quindile aste mancanti e le replico nelle tre dimensioni.

 

Terminata la struttura, seleziono tutte le aste e uso il comando esplodi per far si che le linee siano uniche e non collegate fra di loro. Salvo quindi in formato .dxf (2000) che mi consente di  esportare il file in SAP 2000.

ANALISI DELLA STRUTTURA ATTRAVERSO IL SOFTWARE SAP 2000:

Apro il software di calcolo SAP 2000, impostando come unità di misura kN,m. Attraverso il comando Import, apro il file .dxf e assegno al campo Frames il layer “aste” definito in autocad. Il file, una volta aperto, viene visualizzato su un piano bidimensionale, pertanto devo impostare la vista 3D per poter procedere con l’analisi. La struttura viene visualizzata nella sua estensione tridimensionale, ma ancora non si è definito come essa è vincolata. Seleziono pertanto i quattro vertici alla base della travatura e assegno ad ogni nodo una cerniera: Assign àjoint àRestraints. Queste cerniere sono visualizzate in verde. 

Le aste così rappresentate vengono considerate dal software come unite, mentre sappiamo che in una struttura reticolare esse sono vincolate fra loro da cerniere interne, pertanto rilascio i momenti all’inizio e alla fine: Assign ; Frames ; Releases/Partial Fixity
Procedo quindi assegnando i carichi esterni:
Define ; Load Patterns : Definisco una “forza concentrata”, con fattore di moltiplicazione apri a 0.
Sempre Define ; Load Cases : elimino i carichi DEAD e MODAL.
I carichi esterni devono essere applicati sui nodi superiori della struttura, azione che risulta essere complicata avendo la vista impostata in un piano tridimensionale. Torno quindi sul piano bidimensionale XY per permettere una corretta selezione dei nodi interessati, rendo quindi invisibile la parte della struttura che non deve essere coinvolta nell’operazione di assegnazione dei carichi attraverso:
View ; Set display options ; spunto i campi:  Invisible (Joints),che deve essere disattivato,e attivo Frames Not in View (Frames/Cables/Tendons).

Questa operazione mi permette di selezionare facilmente i nodi a cui deve essere applicata la forza, procedo quindi cliccando su Assign ; Joint Loads ; Forces e impostando come valore della forza (Force Global Z) -40 kN (il segno meno mi indica che la forza è diretta nella direzione della forza gravitazionale). Con il procedimento inverso, attraverso Display Options, rendo visibile nuovamente l’intera struttura. Torno alla vista tridimensionale, che mi permette di visualizzare le frecce delle forze applicate sui nodi.
Procedo ora con l’assegnazione del materiale. Definisco un nuovo materiale:
Define ; Material ; Add new material : lo nomino “acciaio”.
Definisco ora la forma della sezione da assegnare alle aste:
Define ; Section Properties ; Frame sections ; Add new property : Pipe (tubolare).
Pipe section ; rinomino “tubolare” e nel campo Material inserisco il materiale precedentemente creato dell’acciaio.

Seleziono l’intera struttura:
Assign ; Frame ; Frame sections : tubolare. 
Posso ora procedere con l’analisi: Run Analysis. Visualizzo la deformazione e i diagrammi degli sforzi assiali (essendo assenti taglio e momento), Un primo grafico mi indica attraverso colori diversi le aste tese e quelle compresse, un secondo grafico mi permette di visualizzare i valori associati alle singole aste.

Attraverso Display ; Show Tables ; Elements Output, possiamo visualizzare delle tabelle generate dal programma che ci indicano i valori delle sollecitazioni agenti sulle singole aste, in modo tale da poter visualizzare facilmente quelle maggiormente soggette a trazione (+) e compressione (-).